基于未确知聚类法的巷道围岩稳定性预测*

刘　洋，叶义成,2，刘晓云，岳　哲 ，胡南燕

(1. 武汉科技大学 资源与环境工程学院，湖北 武汉 430081；2. 武汉科技大学 冶金矿产资源高效利用与造块湖北省重点实验室，湖北 武汉 430081)

0　引言

巷道围岩稳定是矿山企业安全、高效生产的基础，巷道围岩稳定性分析是合理进行巷道设计与施工、正确选择支护形式与参数的前提和关键，因此有必要对巷道围岩稳定性进行分析评价，从而作出预测[1-2]。

巷道围岩的稳定性预测已有较多成果，许多学者相继提出了模糊数学法、支持向量机法、神经网络法等方法[3-5]。模糊数学法充分考虑到评价过程中的模糊因素，但确定分类指标权值的主观性对预测结果影响较大[6-7]；支持向量机法有效处理各指标间的非线性关系，但参数的选择对分类结果影响明显[8]；神经网络法需要充足计算样本，且易陷入局部最优解[9]。巷道围岩稳定性受岩体质量、围岩材料物理力学性质、裂隙壁状态等多种因素影响，且许多影响因素存在不确定性和隐秘性，因此针对信息具有不确定性的特点展开理论探讨和工程应用研究，非常必要。

未确知信息及其数学处理理论由王光远[10]于1990年提出，是一种不同于模糊信息、随机信息和灰色信息的新的不确定性信息。刘开第等[11]建立了未确知数学理论，并将该理论运用到社会科学和自然科学研究中[12-13]，在此基础上，万玉成[14]提出了未确知聚类理论，其应用研究较多的是未确知聚类预测模型[15-16]。未确知聚类优化法是以均值聚类法处理样本数据、以未确知测度理论构建预测模型，并将一般模型中置信度识别准则改进为最小未确知测度距离原理判别准则。未确知聚类法不仅可以很好处理巷道围岩稳定性预测过程中的未确知信息，也可以避免置信度选取的人为主观因素，从而使模型预测结果更加符合实际。

1　未确知聚类预测优化法

1) 构建巷道围岩稳定性的判别指标体系。设巷道围岩空间为D，若D中的任一巷道围岩Di(i=1，2，…，n)与m个影响因素V1，V2，…，Vm有关，记集合V={V1，V2，…，Vm}为指标集。

2) 对巷道围岩进行分类。将巷道围岩集D={D1，D2，…，Dn}按巷道围岩稳定性分为K类，组成分类集C={C1，C2，…，CK}。

3) 计算巷道围岩稳定性各影响因素的测度值。令pijk=p(xij∈Ck) 为巷道围岩Di的第j个影响因素Vj的实测值xij属于第k个分类Ck的程度大小，pijk即为影响因素的测度值，且需符合以下准则：

0≤p(xij∈Ck)≤1

(1)

p(xij∈C)=1

(2)

(3)

式(2)称为“归一性”，式(3)称为“可加性”。满足式(1)～(3)的p称为未确知测度。

称矩阵(pijk)m×k为单指标测度评价矩阵，且有：

(4)

4)计算巷道围岩稳定性影响因素的权重值。由于巷道围岩稳定性受各影响因素的影响程度具有一定差别，因此，巷道围岩Di中Vj影响因素对巷道围岩稳定性的影响程度用权重系数wj表示。熵权法是根据巷道围岩稳定性各影响因素在各被评价巷道围岩之间的差异大小来确定其权重的大小，可以较好的反映各影响因素信息熵值的效用值。其给出的各影响因素权重比德尔菲法和层次分析法更加准确，避免了主观性，是一种客观赋权的方法。因此，以信息熵理论计算指标权重[17]有：

(5)

(6)

式中：χj为第j个影响因素所提供的信息量。

5) 计算影响因素加权综合测度向量。令pik=p(pi∈Ck)为巷道围岩Di属于第k个分类Ck的程度，pik即为影响因素加权综合测度，有：

(7)

称(pi1，pi2，…，pik)为巷道围岩Di的多指标加权综合测度向量。

6) 预测巷道围岩稳定性类别。令未确知测度距离dk为影响因素加权综合测度pi和pk的距离：

dk=

(8)

按最小未确知测度距离原理预测待测巷道围岩稳定性所属类别。

若

dk0=min(d1，d2，…，dk)

(9)

则说明待预测巷道围岩Dk与分类模式系统要求最接近，可以把待测巷道围岩Dk归入Ck0。

2　巷道围岩稳定性的未确知聚类预测模型

2.1　影响因素选取与样本参数获取

巷道围岩稳定性受众多因素影响，且各因素之间的相互影响也具有不确定性和隐蔽性，是非线性关系，针对不同对象，研究围岩稳定性预测的指标也有一些差异[18-22]。经综合分析选取稳定性评价过程中可以直接获取的、起着主导因素作用的、能较好概括评价体系的评价指标，研究中选取实测RQD值(X1)、单轴抗压强度Rc(X2)以及结构面隙壁状态(X3)。根据指标选取的重要性、独立性、定量性等原则，选取实测RQD值、单轴抗压强度Rc以及结构面隙壁状态已经比较全面。实际应用中，隙壁状态是一个非定量的值，根据工程实践经验对特定的隙壁状态描述特征釆用一定的指标值加以定量化描述，形成隙壁状态的半定量化的评价指标，如表1所示[20]。围岩类别分为5类：Ⅰ为极稳定，Ⅱ为稳定，Ⅲ为中等稳定，Ⅳ为不稳定，Ⅴ为极不稳定。这里以文献[18-22]找到的25组巷道围岩数据作为模型构建样本，具体模型构建样本参数见表2。

表1　隙壁状态定性描述定量化

表2　模型构建样本集

2.2　建立未确知测度函数

已知样本中巷道围岩稳定性等级，可将巷道围岩样本集按围岩等级划分为5类，划分结果见表3。

建立合理的未确知测度函数是用未确知集合反映“不确定性”现象的关键。未确知测度函数主要有直线型、抛物线型、指数分布型等类型，其中直线型未确知测度函数反应属性观测值所处状态变化剧烈程度较小，适用于实测RQD值、单轴抗压强度Rc、结构面隙壁状态指标属性，且直线型未确知测度函数计算简便、应用广泛，具有很强的适应性[23]。

因判别指标较多，且计算原理基本相同，选取实测RQD值为例，建立其直线型未确知测度函数计算表达式如下：

(10)

(11)

(12)

(13)

(14)

表3　样本分类

同理，确定巷道围岩稳定性的3个影响因素的未确知测度函数如图1～3所示。

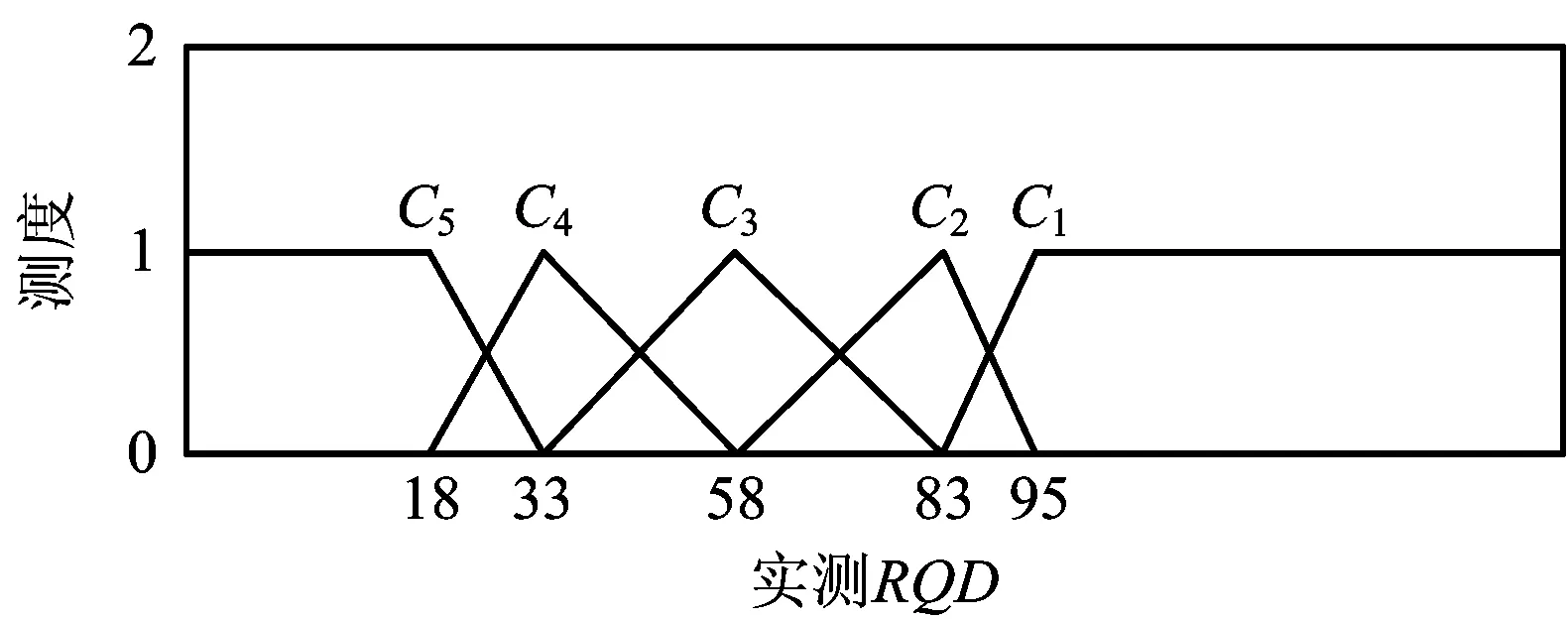
图1　实测RQD的测度曲线Fig.1　Measurement curves of measured RQD

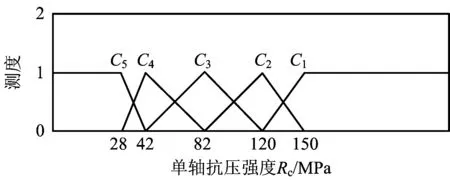
图2　单轴抗压强度的测度曲线Fig.2　Measurement curves of uniaxial compressive strength

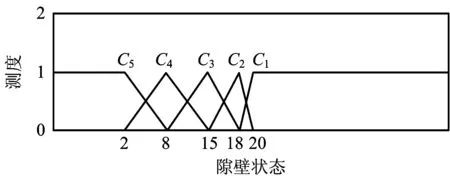
图3　隙壁状态的测度曲线Fig.3　Measurement curves of gap wall condition of structure surface

2.3　模型的检验及应用

将模型构建样本1～25组数据逐一回代入巷道围岩稳定性等级判定的未确知聚类预测模型中，预测准确率达100%，说明该预测模型稳定、合理。该模型在围岩稳定性等级判定方面具有较强的适用性和准确性。

大冶铁矿矿床属接触带型矿床，一般矿岩接触带稳定性差，掘进与支护困难。以大冶铁矿尖林山采区-60 m水平和龙洞采区-62 m水平数列，随机选取具有特征的巷道围岩，统计围岩稳定性评价指标的数据，构建大冶铁矿巷道围岩判别样本，如表4。

将表4中判别样本1的数据代入巷道围岩稳定性的未确知聚类预测模型中可依次计算出判别样本1的实测RQD值、单轴抗压强度、隙壁状态的单指标测度、指标权重。由式(7)计算判别指标的多指标加权综合测度向量为(0，0.122 9，0.603 3，0.273 8，0)，然后用式(8)求得未确知测度距离d1，d2，d3，d4，d5分别为1.205 8，1.099 2，0.497 4，0.952 1，1.205 8，最后根据式(9)可知判别样本1的预测等级为Ⅲ级。同理，知其余4个判别样本的预测等级。表6为大冶铁矿巷道围岩判别样本的多指标综合测度向量、未确知测度距离及预测结果。

表4　大冶铁矿巷道围岩判别样本集

利用BP神经网络对25组样本进行训练，设置输入层节点数3，隐藏层节点数5,输出层节点数1，并对待测巷道进行预测，预测结果如表5。

表5　BP神经网络预测结果

由表6可知采用未确知聚类预测模型所得结果与采用神经网络方法预测结果完全一致，且与工程实际相符。所以，利用未确知测度理论建立巷道围岩稳定性预测模型，并应用于工程实践中是可行、可靠的。

表6　大冶铁矿巷道围岩判别样本预测结果

3　结论

1)综合考虑巷道围岩的物理力学性质，根据未确知测度理论，建立了基于未确知聚类法的巷道围岩稳定性预测模型。选取实测RQD值、单轴抗压强度Rc以及结构面隙壁状态3个指标作为巷道围岩稳定性预测的判别指标，根据实测数据建立各影响因素的未确知测度函数。

2)采用客观赋权法中信息熵理论确定权重，能够避免人为的主观因素对预测结果的影响；采用最小未确知测度距离原理判别准则判定巷道围岩稳定性级别，避免了置信度识别准则中置信度选取的主观因素，使预测结果更符合工程实际。大冶铁矿实例表明：预测等级与BP神经网络预测等级一致，且与巷道围岩实际稳定性相符，巷道围岩稳定性的未确知聚类预测模型可靠，为巷道围岩稳定性预测提供了一种新方法。

[1]刘刚,宋宏伟.巷道稳定性影响因素分析[A]. 全国矿山建设学术会议论文集[C].昆明,2006.

[2]冯伟,韩立军,刘灿灿.水平应力对半圆拱形巷道围岩应力分布及变形特征影响[J].中国安全生产科学技术,2012,8(12):21-26.

FENG Wei,HAN Lijun, LIUCancan. Influence of horizontal stress on stress distribution and deformation characteristics around arched roadway[J]. Journal of Safety Science and Technology, 2012, 8(12): 21-26.

[3]李宁,张承客,刘乃飞.围岩稳定性评判方法适用范围探讨[J].岩土工程学报,2014,36(2):382-388.

LI Ning， ZHANG Chengke，LIU Naifei．Applicability of stability criterion for tunnels[J].Chinese Journal of Geotechnical Engineering,2014,36(2):382-389.]

[4]牛少卿,杨双锁,李义.基于岩体强度理论的巷道围岩稳定性分级[J].金属矿山,2013,450(12):16-19.

NIU Shaoqing，YANG Shuangsuo，LIYi．Surrounding rock's stability classification of roadway based on rock mass strength theory[J].Metal Mine, 2013(12):16-19.

[5]刘浩,邵海,刘欣,等.基于加权平均法修正BQ法的巷道围岩稳定性分级应用研究[J].中国矿业,2015,24(4):91-95.

LIU Hao,SHAO Hai,LIU Xin,et al. Application study on roadway surrounding rock stability classification based on BQ method revised with weighted average method[J]. China Mining, 2015, 24(4): 91-95.

[6]李洪,蒋金泉,张开智.回采巷道围岩分类的模糊聚类分析方法[J].西安科技大学学报,2005,25(1):12-16.

LI Hong,JIANG Jinquan, ZHANG Kaizhi. Fuzzy clustering analysis of tunnel surrounding rock classification [J].Journal of Xi’an University of Science & Technology,2005,25(1): 12-16.

[7]Y.C.Ye, N. Yao, Q.Z. Wang, et al, A method of ranking interval numbers based on degrees for multiple attribute decision making, Journal of Intelligent & Fuzzy Systems, 2014， 30(1)：211-221.

[8]朱一丁,马文涛.回采巷道围岩分类的支持向量机方法[J].采矿与安全工程学报,2006,23(3):362-365.

ZHU Yiding, MA Wentao. Method of support vector machines for classifying surrounding rocks of gateways[J].Journal of Mining & Safety Engineering,2006,23(3):362-365.

[9]贺超峰,华心祝,马菁花,等.基于BP神经网络的回采巷道围岩稳定性分类[J].矿业工程研究,2012,27(3):6-9.

HE Chaofeng,HUA Xinzhu,MA Jinghua,et al.Classification of surrounding rock stability of roadway based on BP Neural Network[J]Mineral Engineering Research,2012,27(3):6-9.

[10]王光远.论未确知性信息及其数学处理[J].哈尔滨建筑工程学院学报,1990,23(4):52-58.

WANG Guangyuan. Uncertainty information and its mathematical treatment[J]. Journal of Harbin Architecture and Engineering Institute, 1990, 23(4): 52-58.

[11]刘开第,吴和琴,庞彦军,等.不确定信息数学处理及应用[M].北京: 科学出版社, 1999: 20-89.

[12]宫凤强,李夕兵,董陇军,等.基于未确知测度理论的采空区危险性评价研究[J].岩石力学与工程学报,2008,27(2):323-330.

GONG Fengqiang,LI Xibing,DONG Xiaojun,et al. Underground goaf risk evaluation based on uncertainty measurement theory[J].Chinese Journal of Rock Mechanics and Engineering, 2008(2):323-330.

[13]程爱平,高永涛,季毛伟,等.基于未确知测度理论的煤矿底板突水量预测[J].金属矿山, 2014, 43(8): 157-161.

CHENG Aiping, GAO Yongtao, JI Maowei, et al. Forecast of water in-rush from coal floor based on unascertained measure theory[J].Metal Mine, 2014(8):157-161.

[14]万玉成. 基于未确知性的预测与决策方法及其应用研究[D].南京:东南大学, 2004.

[15]董陇军,李夕兵,宫凤强,等.地下开采引发地面沉陷的未确知聚类预测方法[J].中国地质灾害与防治学报,2008,19(2):95-99.

DONG Longjun, LI Xibing, GONG Fengqiang. Predicting surface subsidence induced by mining based on unascertained clustering method[J]. The Chinese Journal of Geological Hazard and Control, 2008, 19(2): 95-99.

[16]赵国彦,吴浩.未确知聚类方法及其在松动圈厚度预测中的应用[J].科技导报,2013,31(2):50-55.

ZHAO Guoyan,WU Hao. Application of unascertained clustering method for predicting the thickness of excavation damaged zone[J]. Science & Technology Review, 2013, 31(2):50-55.

[17]曹庆奎,刘开展,张博文.用熵计算客观型指标权重的方法[J].河北建筑科技学院学报,2000,17(3):40-42.

CAO Qingkui, LIU Kaizhan, ZHANG Bowen. Calculation method of objective index weight by entropy[J].Journal of Hebei Institute of Architectural Science and Technology, 2000,17(3):40-42.

[18]王薇,邹江海,潘文硕,等.不同施工顺序对陡坡偏压小净距隧道围岩稳定性的影响研究[J]. 中国安全生产科学技术,2016,12(8):28-33.

WANG Wei, ZOU Jianghai, PAN Wenshuo, et al. Study on influence to stability of surrounding rock by different construction sequence for bias tunnel with small interval and steep slope [J]. Journal of Safety Science and Technology, 2016, 12(8): 28-33.

[19]朱志洁,张宏伟,韩军,等.不同应力场条件下巷道稳定性研究[J]. 中国安全生产科学技术, 2015, 11(11):11-16.

ZHU Zhijie,ZHANG Hongwei， HAN Jun, et al. Research on stability of roadway under different conditions of stress field[J]. Journal of Safety Science and Technology, 2015, 11(11):11-16.

[20]邹灿.大冶铁矿井下开采巷道围岩稳定性分析及控制技术研究[D].武汉:中国地质大学(武汉),2014.

[21]施耀斌，叶义成，王其虎,等. 缓倾斜多层矿床条带法开采矿柱变形特征及开采强度模拟[J]. 矿冶工程, 2015, 35(5)：4-9.

SHI Yaobin, YE Yicheng, WANG Qihu, et al. Pillar deformation char-acteristic for multilayer gently-dipping deposits by strip mining andmining intensity simulation[ J]. Mining and Metallurgical Engineering, 2015, 35(5):4-9.

[22]王其虎.地下开采中接触带复合岩体非协调变形及控制研究[D].武汉:武汉科技大学,2015.

[23]董陇军,李夕兵,宫风强. 膨胀土胀缩等级分类的未确知均值聚类方法及应用[J]. 中南大学学报:自然科学版, 2008,39(5):1075-1080.

DONG Longjun, LI Xibing, GONG Fengqiang. Unascertained average clustering method for classification of grade of shrink and expansion for expansive soils and its application[J]. Journal of Central South University (Science and Technology), 2008, 39(5): 1075-1081.