可重复使用飞行器鲁棒自抗扰控制*
陈上上,何英姿
(1.北京控制工程研究所,北京100094;2.空间智能控制技术重点实验室,北京100094)
可重复使用飞行器鲁棒自抗扰控制*
陈上上1,2,何英姿1,2
(1.北京控制工程研究所,北京100094;2.空间智能控制技术重点实验室,北京100094)
为可重复使用飞行器再入提出一种新的鲁棒自抗扰控制方法.针对一般多输入多输出模型,重新定义状态变量后,分别设计各通道的线性扩张状态观测器.之后提出自抗扰控制系统的一套鲁棒分析与设计方法.应用于姿态控制时,引入最速跟踪微分器对姿态角指令进行滤波,以解决倾侧角反转过程中快速性与抗饱和之间的矛盾.仿真结果表明,设计的控制系统解耦效果良好,鲁棒稳定性较强,饱和问题也得到解决.
鲁棒;自抗扰控制;抗饱和;解耦
0 引言
为了提高可重复使用飞行器(reusable launch vehicle,RLV)的可靠性与安全性并降低成本,美国航空航天局先后支持研究了滑模变结构控制[1]、动态逆控制[2]等方法.文献[3-6]分别研究了模型预测控制、模型参考自适应控制、滑模观测器与滑模控制器、基于特征模型的自适应控制等先进方法,解决了RLV再入过程中的易饱和、强耦合、强不确定性以及大扰动等问题.
再入过程中存在诸多不确定性,导致对模型依赖程度较大的控制方法不再适用;传统鲁棒控制方法比较保守,不确定性较大时难以兼顾鲁棒性与其他性能指标;各种先进非线性控制方法还远未成熟.因此,增益调度方法在实际工程中仍占据主导地位.
模型参数不确定性对线性自抗扰控制系统的稳定性与性能指标的影响都很小,我们在文献[7]中给出了该系统鲁棒性的几种分析方法,本文采用μ分析研究该系统的鲁棒稳定性,进而提出一种鲁棒自抗扰控制(robust active disturbance rejection control,RADRC)方法,克服原有参数试凑方法与经验选取方法的缺陷,并应用到RLV再入姿态控制.
1 鲁棒自抗扰控制
1.1 线性自抗扰控制
考虑一般非线性多输入多输出(multi-input multi-output,MIMO)系统


1.2 鲁棒分析
闭环系统由式(4)~(6)的误差模型、ESO和反馈控制律组成,考虑原始模型(1)中的参数不确定性,把该闭环系统转化为图1所示的线性分式变换形式.
其中:Gμ(s)为定常模块;Θ为不确定模块:
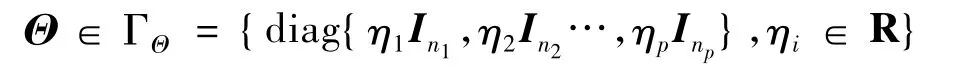
其中Ini表示ni×ni单位阵.
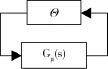
图1 闭环系统的线性分式变换Fig.1 Linear fractional transformation of the closed-loop system
假设6.
用μΔ表示结构奇异值,定理1给出了闭环系统鲁棒稳定的一个充分条件.
定理1.如果假设1~6成立,则存在常数ε0>0,使得对满足的任意初始状态ξ0,闭环系统是小信号有限增益Lp稳定的,当(1)Gμ(s)是赫尔维茨的;(2)
1.3 鲁棒控制器
基于定理1,可以对控制参数进行优化设计,以提高闭环系统的鲁棒稳定性.另外,兼顾控制品质要求与执行机构能力限制,对控制参数的选取范围加以限定:Ko∈Πo,K∈Π,其中,Πo、Π为相应的限定范围.
令Gμ(s)所有极点的最大实部为υ,以模型参数不确定范围最大为优化指标,以定理1的成立条件为约束,以控制参数为待优化变量,考虑其限定范围,相应的优化问题为:
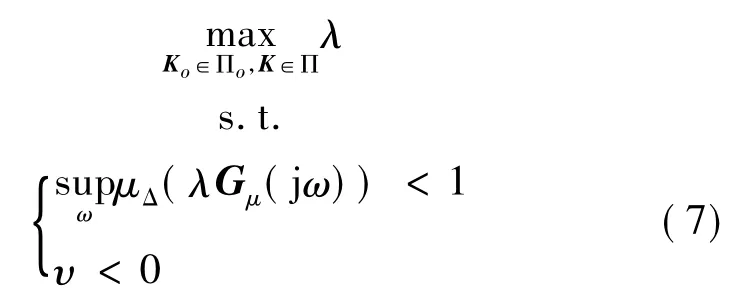
2 运动方程
忽略平动等影响,RLV再入姿态运动方程为
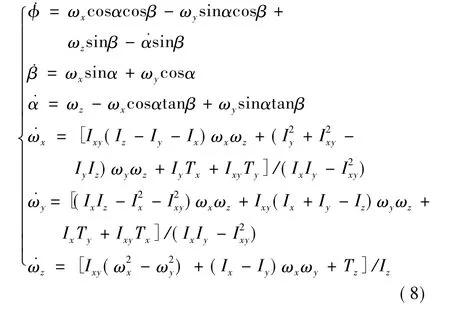
式中,φ、β、α分别为倾侧角、侧滑角、攻角,ωx、ωy、ωz为滚转、偏航、俯仰角速度,Tx、Ty、Tz分别为气动力矩在体坐标系3轴分量:
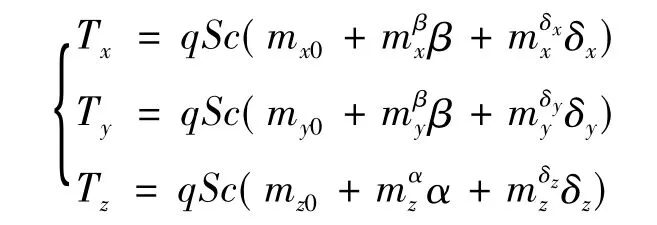
式中,q为动压,S为参考面积,c为参考长度,δx、δy、 δz为滚转、偏航、俯仰舵偏,为气动系数.
3 姿态控制律设计
3.1 线性自抗扰姿态控制律设计
RLV姿态线性误差模型为

把ESO极点配置为重极点,控制参数形式为
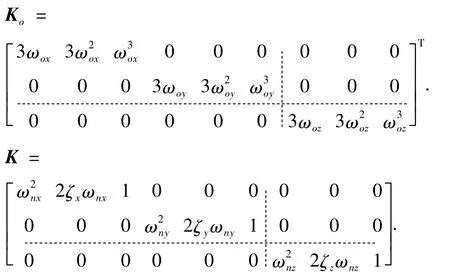
3.2 鲁棒控制律设计
侧滑角参考值为零时纵向通道与侧向通道是解耦的,因此本节分别针对这两个通道进行鲁棒设计.

侧向通道的不确定模块为
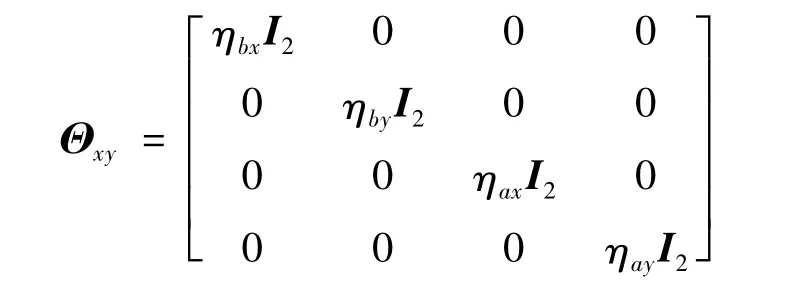
假设侧向通道模型参数偏差满足
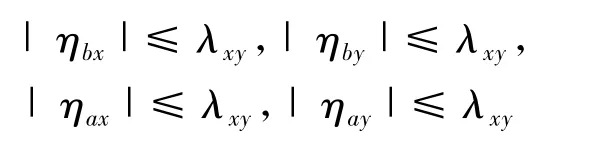
特征点模型参数取值为:

偏航与滚转选用相同控制参数,并限定范围:
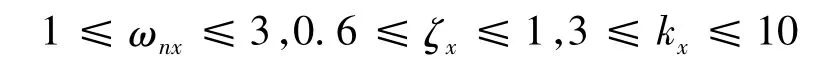
优化结果为:
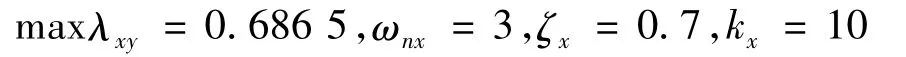
对俯仰通道令
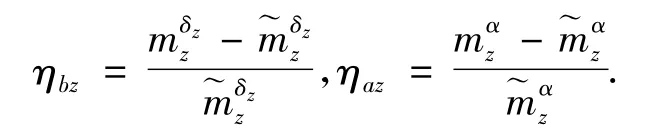
不确定模块为
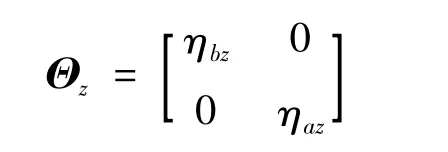
假设俯仰通道模型参数偏差满足

令λz=diag{λbz,λaz},若给定λbz=λbz1,由定理1可得允许的λaz的最大值λaz1,此为模型参数不确定性的一个边界,即图2中以点P1(λaz1,λbz1)、P2、P3、P4为顶点的矩形.逐点给定λbz,可以得到对应的λaz,进而得到一组矩形边界.由这些矩形的顶点构成模型参数不确定性最大边界,如图2所示.
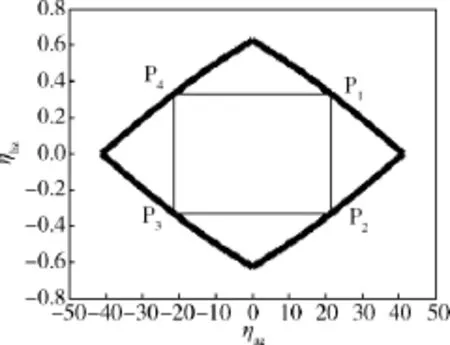
图2 模型参数不确定性边界Fig.2 Model parameter uncertainty bound
特征点模型参数取值为:
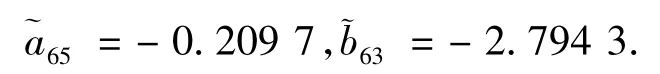
限定控制参数范围:
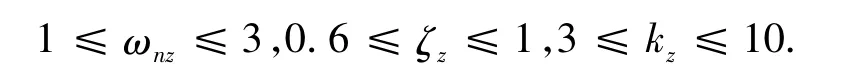
选取舵效不确定性范围为优化目标,优化结果为:
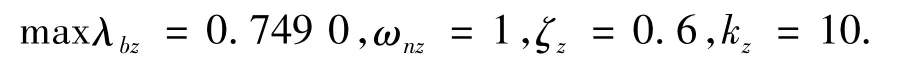
3.3 抗饱和设计
RLV再入过程中需要几次倾侧角反转机动,为了防止饱和,本文采用最速跟踪微分器[8](tracking differentiator,TD)对倾侧角指令进行滤波处理:

式中,Ts为采样时间,fhan()为最速控制综合函数,
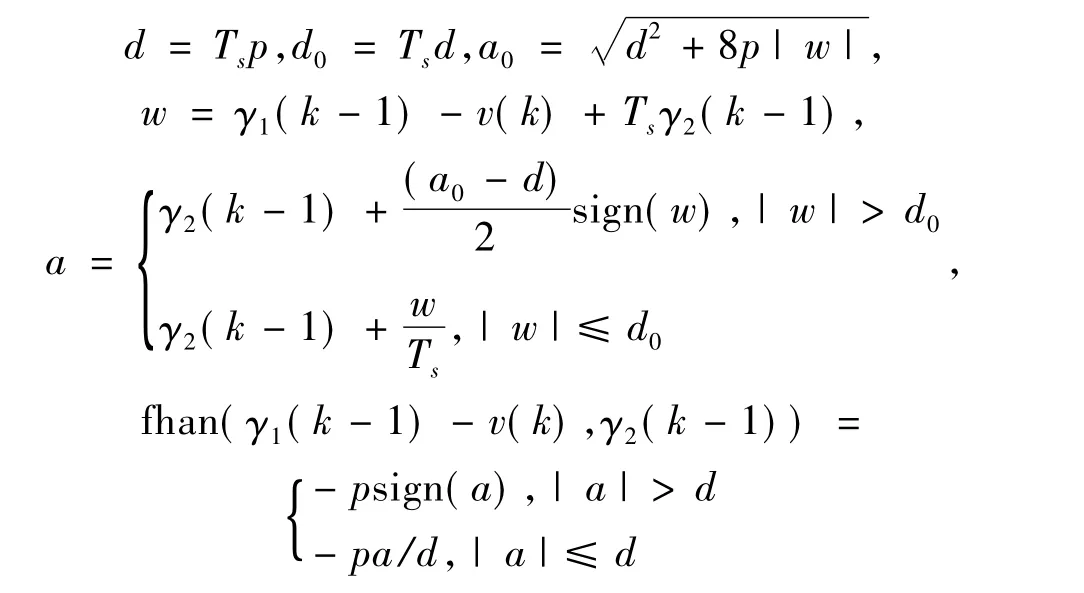
输出γ1将在的限制下最快的跟踪输入v.
根据机动任务的快速性需求,结合RLV控制系统能力,TD参数设计为p=0.03.
4 仿真验证
4.1 鲁棒解耦验证
以某RLV再入为背景,考虑模型参数不确定性,静稳定性降低:ηaz=-10、ηax=ηay=-0.3,舵效降低:ηbx=ηby=ηbz=-0.3,针对倾侧角反转机动进行仿真,结果如图3~6所示.存在模型参数不确定的情况下,倾侧角反转过程中,RADRC系统响应速度比PID系统更快;RADRC系统各舵偏响应发生严重饱和,导致各状态量的振荡幅值较大,PID系统未发生控制饱和,各状态量的振荡幅值较小.
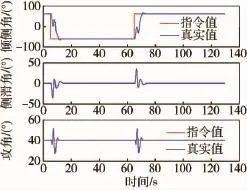
图3 RADRC系统姿态角跟踪Fig.3 Attitude tracking of RADRC system
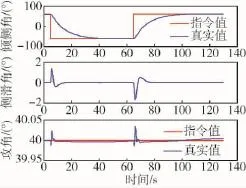
图4 PID系统姿态角跟踪Fig.4 Attitude tracking of PID system
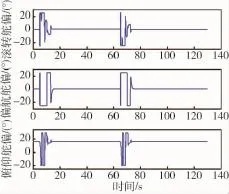
图5 RADRC系统舵偏响应Fig.5 Aerosurface response of RADRC system
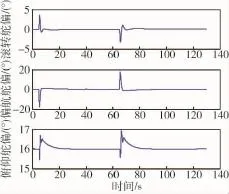
图6 PID系统舵偏响应Fig.6 Aerosurface response of PID system
4.2 抗饱和验证
引入最速TD,仿真结果如图7~8所示.
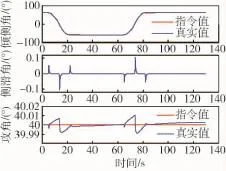
图7 RADRC系统姿态角跟踪Fig.7 Attitude tracking of RADRC system

图8 RADRC系统舵偏响应Fig.8 Aerosurface response of RADRC system
仿真结果表明使用TD后,倾侧角反转机动过程中,各舵偏角未发生饱和,且各姿态角跟踪良好,偏航与俯仰通道受到的耦合作用微弱.
5 结论
本文针对RLV再入过程中面临的强耦合、强不确定性、易饱和等问题,提出了一种RADRC方法.该方法通过MIMO的ESO进行解耦补偿,通过优化控制参数提高鲁棒稳定性,通过最速TD滤波实现抗饱和.仿真结果验证了该方法的有效性.
[1]WALLNER E M,SHTESSEL Y.Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance,Control and Dynamics,2006,29(6):1315-1328.
[2]DOMAN D B,NGO A D.Dynamic inversion-based adaptive-reconfigurable control of the X-33 on ascent[J].Journal of Guidance,Control and Dynamics,2002,25 (2):275-284.
[3]VANSOEST W R,CHU Q P,MULDER J A.Combined feedback linearization and constrained model predictive control for entry flight[J].Journal of Guidance,Control and Dynamics,2006,29(2):427-434.
[4]MOOIJ E.Numerical investigation of model reference adaptive control for hypersonic aircraft[J].Journal of Guidance,Control and Dynamics,2001,24(2):315-323.
[5]董琦,宗群,王芳,等.基于光滑二阶滑模的可重复使用运载器有限时间再入姿态控制[J].控制理论与应用,2015,32(4):448-455.DONG Q,ZONG Q,WANG F,et al.Finite time smooth second-order sliding-mode controller design for reentry reusable launch vehicle[J].Control Theory&Applications,2015,32(4):448-455.
[6]龚宇莲,吴宏鑫.基于特征模型的高超声速飞行器的自适应姿态控制[J].宇航学报,2010,31(9):2122-2128.GONG Y L,WU H X.Characteristic model-based adaptive attitude control for hypersonic vehicle[J].Journal of Astronautics,2010,31(9):2122-2128.
[7]陈上上,何英姿,刘贺龙.线性自抗扰控制鲁棒稳定性分析[J].控制理论与应用,2016,33(5):662-668.CHEN S S,HE Y Z,LIU H L.On robust stability of linear active disturbance rejection control system[J].Control Theory&Applications,2016,33(5):662-668.
[8]韩京清,袁露林.跟踪微分器的离散形式[J].系统科学与数学,1999,19(3):268-273.HAN J Q,YUAN L L.The discrete form of trackingdifferentiator[J].Journal of Systems Science and Mathematical Sciences,1999,19(3):268-273.
Robust Active Disturbance Rejection Control for a Reusable Launch Vehicle
CHEN Shangshang1,2,HE Yingzi1,2
(1.Beijing Institute of Control Engineering,Beijing 100094,China;
2.Science and Technology on Space Intelligent Control Laboratory,Beijing 100094,China)
A novel robust active disturbance rejection control approach is presented for a reusable launch vehicle during reentry.The state variables of a general multi-input multi-output model are redefined so that the linear extended state observers of every channel can be designed separately.Then a robust analysis and design methodology is proposed for the active disturbance rejection control system.When this methodology is applied to attitude control,the attitude command is filtered by the steepest tracking differentiator to deal with the contradiction between response speed and anti-windup performance during bank reversal.Simulation results show that the designed control system is well decoupled and quite robust and the saturation problem is solved.
robust;active disturbance rejection control;anti-windup;decoupling
TP273
A
1674-1579(2017)01-0025-05
10.3969/j.issn.1674-1579.2017.01.004
陈上上(1982—),男,博士研究生,研究方向为再入制导控制;何英姿(1970—),女,研究员,研究方向为空间操作控制技术和空天飞行器GNC技术等.
*国家自然科学基金资助项目(61403030)和(61304037).
2016-10-20

