构造平行四边形证明三角形三条高所在直线交于一点

江苏省兴化市顾庄学校(225724) 李 霞 ●

江苏省兴化市安丰水初级中学(225766) 张建权 ●

构造平行四边形证明三角形三条高所在直线交于一点

江苏省兴化市顾庄学校(225724) 李 霞 ●

江苏省兴化市安丰水初级中学(225766) 张建权 ●

一、问题的提出

众所周知，三角形的三条高、三条中线和三条角平分线所在直线都分别交于一点．在这三个命题中，三角形的三条高所在直线交于一点最难证明，原因有两个:一、要对三角形进行分类;二、要么所需知识超出教材范围，要么过程极其复杂．苏教版教材没有对此进行证明，只是在初一学习“三角形的高”时让学生动手操作感受一下，这不能不说是一种遗憾．

那么，有没有一种方法既不超出教材范围，过程又比较简单呢?下面本文将呈现这样的方法，以供同行分享借鉴，不当之处，还望批评指正．

二、证明过程

在苏教版教材八年级上册第二章《轴对称图形》第2．4节中，有这样一道例题:

如图1(1)，在△ABC中，AB、AC的垂直平分线l1、l2相交于点O．证明:点O在BC的垂直平分线上．

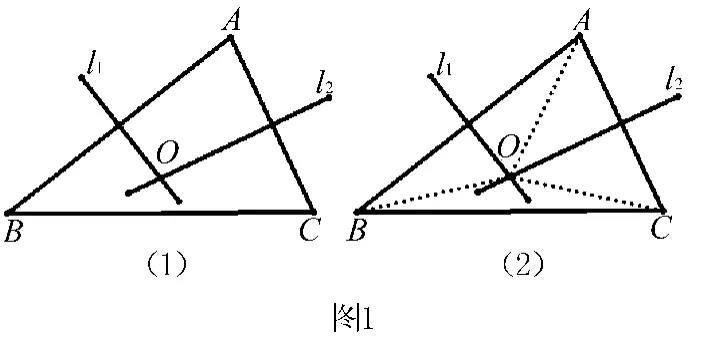
其证明过程很简单，如图1(2)，连接OA、OB、OC．因为点O在AB的垂直平分线上，所以OA=OB，同理OA= OC，从而OB=OC，所以点O在BC的垂直平分线上．学生在初三学习了三角形的外接圆后，知道这个点O即为三角形的外心．这道例题本质上揭示了这样一个结论，即三角形三边的垂直平分线交于一点．

如果能通过某种方法，将三角形三条高所在直线交于一点转化为另一个三角形三边的垂直平分线交于一点，那么就形成了本文所要呈现的方法，其过程如下:

一、当三角形为直角三角形时．

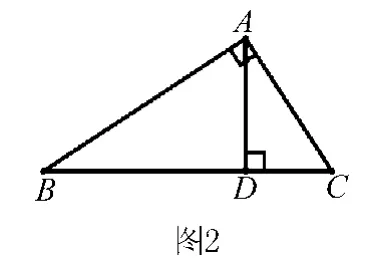
如图2，其三条高所在直线显然交于一点．

二、当三角形为锐角三角形时．

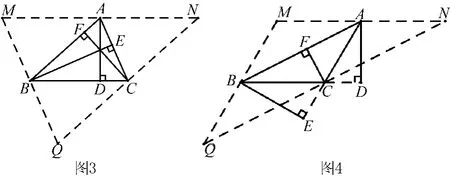
如图3，分别过三角形的三个顶点作对边的平行线，交点分别为M、N、Q，由MN∥BC，AB∥QN可知，四边形ABCN为平行四边形，所以AB=CN．再由MQ∥AC，AB∥QN可知，四边形ABQC为平行四边形，所以AB=QC，因此NC=QC，即点C为QN的中点．再由CF⊥AB，AB∥QN得，CF⊥QN，所以CF垂直平分QN．同理，BE垂直平分MQ，AD垂直平分MN．因此，AD、BE、CF分别垂直平分MN、MQ、QN．根据“三角形三边的垂直平分线交于一点”得，AD、BE、CF交于一点．

三、当三角形为钝角三角形时．

如图4，分别过三角形的三个顶点作对边的平行线，交点分别为M、N、Q，其证明过程与第二种情形一致．

从证明过程可以看出，虽免不了对三角形的形状进行分类，但这并没有对证明方法和难度产生影响．证明过程只是包含了平行线的性质、平行四边形的判定及性质和“三角形三边的垂直平分线交于一点”这一结论，应该说难度很小，学生很容易理解和接受．

教材在初二《轴对称图形》这一章中出现了证明三角形三条角平分线交于一点的例题，在初三《图形的相似》这一章中利用中位线的性质对三角形三条中线交于一点进行了证明，唯独没有出现三角形的三条高所在直线交于一点的证明，这个遗憾只能由教师去弥补了．教材在证明中位线定理时也是构造了平行四边形，教师不妨在讲中位线定理之前介绍文中的证明方法，这样既弥补了教材的遗憾，又巩固了几何证明中的构造平行四边形的方法．

G632

B

1008－0333(2017)02－0014－01