文献老化B-K方程的改进式

时秀娟，李正吾

（1.仰恩大学 数学系，福建 泉州 362014；2.五邑大学 离退老干处，广东 江门 529020）

文献老化B-K方程的改进式

时秀娟1，李正吾2

（1.仰恩大学 数学系，福建 泉州 362014；2.五邑大学 离退老干处，广东 江门 529020）

针对文献老化B-K方程在实际应用中存在系数a,b的取值会超出[0，1]范围的问题，将B-K方程中的ex或e2x修改为enx，用改进后的方程进行数据模拟. 结果表明，对B-K方程的改进，不仅有合理的意义，也提高了模拟的精度，特别是可以解决B-K方程中有权重意义的系数a,b的取值范围问题.

文献老化；B-K方程；B-K方程的改进式

科技文献老化是指随着时间的推移其利用价值逐渐衰减的现象[1]. 文献老化的概念最早是1944年美国人戈斯内尔（C.F.Gosnell）[2]提出来的，在对科技文献老化的研究过程中，应用广泛的模型和理论主要有Burton-Kebler方程（简称为B-K方程）和莫德列夫对B-K方程的修正（简称为B-K方程莫氏修正式）[3]. 国内外很多学者也对这些模型做了一系列的研究[4-6]，并结合实例展现了B-K方程模拟文献老化的高精确性，以及方程中出现的参数的合理意义. 但是，文献[7]和文献[8]因对B-K方程和B-K方程莫氏修正式的错误处理，导致结论几乎是错误的. 本文分析了其错误，对B-K方程做了适当的改进，以便能更好地反映不同学科的情况，并确保a,b不超出[0，1]范围，且本文所有的结论都有合理的解释.

1 B-K方程莫氏修正式中系数a,b的约束条件

文献老化B-K方程形如：

式中，y为被引文献的累积百分比；x为时间（10年为单位）；a,b为待定系数，分别视为“档案性”文献和“有现时作用”文献在被引文献中所占百分比（或理解为权重）[5].

B-K方程莫氏修正式：

B-K方程是将研究老化的当年对应的时刻定义为x=0；而修正式是将研究老化的当年称为第1年，对应的时刻为x=0.1，在B-K方程的莫氏修正式中时间x不能等于零. 由于二者的区别仅是初始时刻的选取问题，B-K方程的莫氏修正式已是多此一举，文献[7]为使B-K方程的莫氏修正式也能取x=0，将式（2）改为：

进一步，式（3）可写为：y=1-(ae0.1e-x+be0.2e-2x)，ae0.1+be0.2=1. 可以发现，式（3）与式（1）没有区别.

文献[7]还有下面的结果，即由式（3）求得文献引文比率对时间的变化率并将ae0.1+be0.2=1代入得：

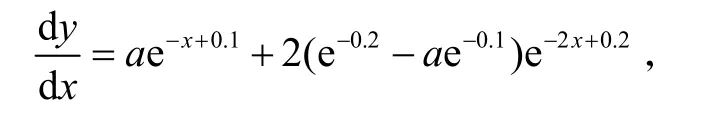
为了保证变化率大于零，得到对系数的又一约束条件：0≤a≤2e0.1. 事实上，由于2e0.1≈2.210 34，取a=2.21(＜2e0.1)，在时间x=0.1处，可算得变化率等于-0.151 92，是个负数，因此，该约束条件并不能保证变化率大于零.

另外，文献[7]中将0≤a≤2e0.1代入ae0.1+be0.2=1，得到：1-2e0.1≤b≤1也是不合理的. 因为当a=0取得最小值时，根据ae0.1+be0.2=1，应得到b≤e-0.2. 同样当a=2e0.1取得最大值时，应得到b≥e-0.2-2.因此，文献[7]对莫氏修正式中系数a,b给出的约束条件都是错误的.

目前科技文献老化的指标用半衰期描述，文献[8]指出：“对于某科技文献而言，其系数a应该是一定的，所以该科技文献老化的半衰期与其出版年龄T成正比. 因此，在科技文献老化研究中，T取值不同，科技文献老化的半衰期是不同的.”这结论其实是不合理的. 文献[8]以两个B-K老化方程为例来说明这种情况，分别取T1=10年和T2=5年，两种情况下的系数a=0.9,b=0.1，即有：

由式（4）和式（5）算出的结果如表1所示.

表1 T1=10年和T2=5年，不同x的取值与对应的y值

对于B-K公式而言，T其实是时间单位，当T1=10时，x=1表示10年，即x1=10；当T2=5时，x=1表示5年，即x2=5，从而有，也就是说式（4）中x=1表示时间是1年，式（5）中x=1表示时间是2年. 表1给出的半衰期为x1=6.44,x2=3.22，这说明式（4）和式（5）的计算结果是相同的，并非二者半衰期不同. 其实，文献的半衰期本是客观事实，是不会随T的变化而变化的.

另外，文献[8]中关于B-K方程系数a,b的约束条件也存在错误. 利用方程a+b=1求文献引文比率对时间的变化率时，要求，本应得到，而文献[8]却得到：

因此，文献[8]的推导是错误的，其关于B-K方程中系数a,b给出的约束条件也是错误的.

2 B-K方程的改进式

过去生产的文献可分为两类：一类是“档案性”文献，一类是“有现时作用”的文献[9].前者老化较慢，后者老化较快.在文献[5]中，将式（1）变形，令1-y=z1+z2，其中z1=ae-x，z2=be-2x，则有：. 即

可见，z1的变化速度等于z1，而z2的变化速度是z2的两倍，从而z2的相对变化率是z1的两倍. 因此，文献[5]作者将B-K方程中的第1项z1=ae-x定义为“档案性”文献对文献老化的贡献，第2项z2=be-2x定义为“有现时作用”文献对文献老化的贡献. B-K方程反映了“档案性”文献和“有现时作用”文献的变化速度的快慢，即B-K方程把“有现时作用”文献的相对老化速度定义成“档案性”文献的两倍. 但在实际研究过程中，特别是在知识发展迅速的时代，统统定义为两倍是与实际不符的，两倍并不能完全反映所有学科文献老化的情况. 因此，本文对B-K方程做了3种改进.

1）B-K方程改进为：y=1-(ae-x+be-nx),a+b=1，即：

此处，n根据不同的学科取不同的值. 即不同学科的相对老化速度要有所区别，譬如，有的学科n取2，有些学科n会小于2或者超过2.

这里，以《五邑大学学报（自然科学版）》引文资料（见表3）为例，以前两年至前17年的资料数据，用改进式（6）模拟得到n=1.09,a=0.12，此时方程为y=1-（0.12e-x+0.88e-1.09x），此时的误差平方和是1.588%.

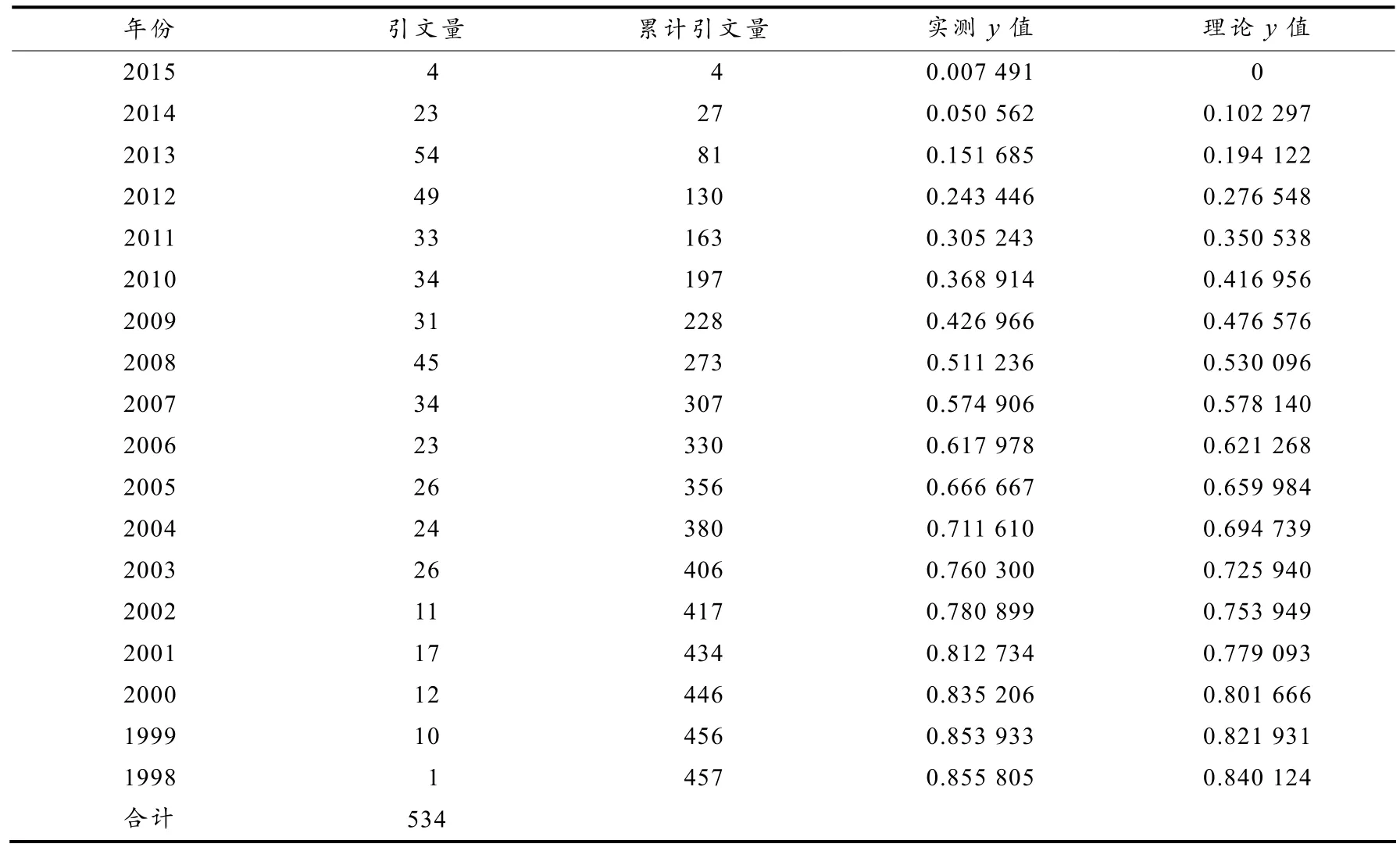
表3 《五邑大学学报（自然科学版）》引文资料及计算结果

2）B-K方程改进为：

这里，利用《中国科学·数学》杂志的引文资料（见表4），以前两年至前17年的资料数据，用改进式（7）模拟得到n=0.64,a=0.92，此时方程为y=1-（0.92e-0.64x+0.08e-2x） ，误差平方和是0.014 8%.

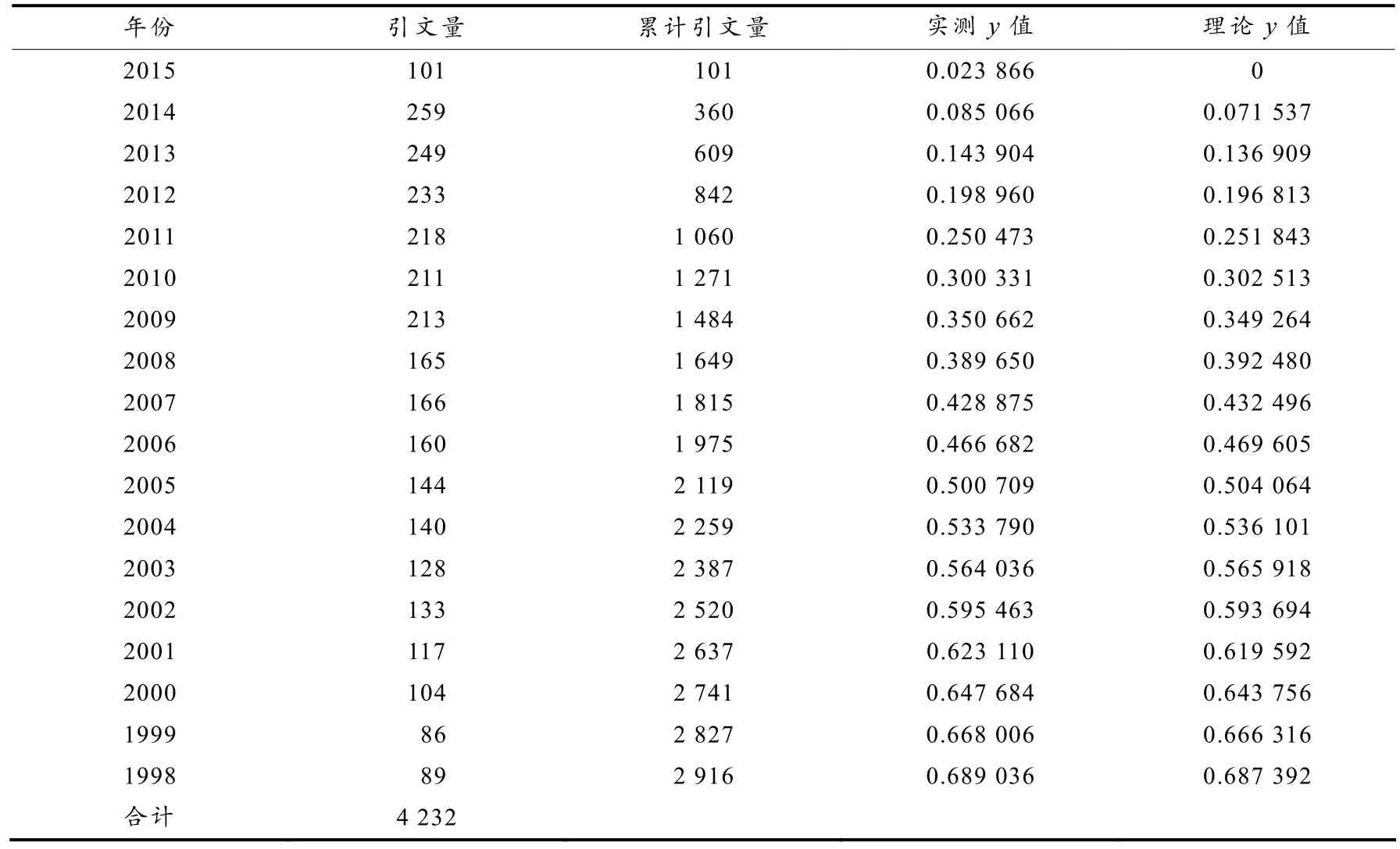
表4 《中国科学·数学》引文资料及计算结果

由此可以看出，无论是单一学科还是综合学科，B-K方程改进式都有合理的和较好的模拟效果.

3）为了更好地反映不同学科的情况，还可将B-K方程改进为如下形式：

3 B-K方程改进式中a与n的相关性

文献[5]也提到，如果考虑到a+b=1，把a和b分别视为“档案性”文献和“有现时作用”文献在被引文献中所占百分比（或理解为权重），这在理论上是完美的，也是合理的. 但必须要求a与b均不小于零. 然而，在实际应用中，会出现a＜0或a＞1的情形（文献[9]认为a＜0和a＞1的情况是一种异常），B-K方程改进式解决了这个问题.

a＜0时，用B-K方程改进式（6），将其变形可得：

由此可以看出，当a＜0时，B-K方程改进式（6）中的a和n是正相关的，a随着n的增加而增加. 因此，当B-K方程（1）中a＜0时，增加B-K方程改进式（6）中的n值，使之大于2，可以让a在[0,1]内取值. 因为a＜0意味着“档案性”文献占的份额过小，将“有现时作用”文献老化速率定义为大于2，使符合“有现时作用”文献的数量减少，从而使符合“档案性”文献的数量增加，以实现a＞0的目的.

当a＞1时，用B-K方程改进式（7），将其变形可得：

由此可以看出，当a＞1时，B-K方程改进式（7）中的a和n是正相关的，a随着n的减小而减小. 因此，当B-K方程（1）中a＞1时，减少B-K方程改进式（7）中的n值使之小于1，可以让a在[0，1]内取值. 因为a＞1意味着“档案性”文献占的份额过大，将“档案性”文献老化速率定义为小于1，使符合“档案性”文献的数量减少，以实现a＜1的目的.

例如，用《中国科学·数学》杂志的引文资料（见表4），以前两年至前17年的资料数据，用B-K方程（1）模拟结果为a=1.53（误差的平方和是1.576%），此时a超出了[0，1]范围，这与a,b为权重的思想不符. 此时用B-K方程改进式（7）模拟数据，让n从1变为0.64，可得a=0.92（误差平方和是0.014 8%）. 因为《中国科学·数学》所引用的论文一般比较经典，一般认为经典学科老化的速度比较慢，因此将“档案性”文献老化速率定义为比1小，“档案性”文献的数量随之减少，故有a＜1. 另外，这样改进以后，还可以保证文献引文比率对时间的变化率

[1] 靖培栋，刘忠厚. 科技文献经典老化模型的新修正[J]. 情报学报，1999, 18(2): 85-90.

[2] GOSNELL C F. The rate of obsolescence in college library book collections by an analysis of three select lists of books for college libraries [M]. NewYork: New York University, 1943.

[3] 邱均平. 信息计量学（三）[J]. 情报理论与实践，2000, 23(3): 237-240.

[4] 丁星，刘俊. Burton-Kebler方程分析方法的改进[J]. 情报学报，1995, 14(3): 227-233.

[5] 李正吾. 文献老化B-K方程分析[J]. 情报科学，1999, 17(4): 429-433.

[6] 韦秀先. 文献老化B-K方程机理分析[J]. 情报杂志，2005, (4): 14-15, 13.

[7] 陈京莲. B-K方程的莫德列夫修正式的约束条件[J]. 现代情报，2009, 29(9): 15-16.

[8] 陈京莲. B-K方程系数的约束条件及半衰期公式的修正[J]. 情报杂志，2007, 26(4): 25-26.

[9] 王崇德. 文献计量学引论[M]. 桂林：广西师范大学出版社，1997.

[责任编辑：熊玉涛]

The Improved B-K Equation for Literature Obsolescence

SHI Xiu-juan1, LI Zheng-wu2
(1. Department of Mathematics, Yang-en University, Quanzhou 362014, China; 2. Retired Veteran Cadres Department, Wuyi University, Jiangmen 529020, China)

In view of the fact that in the practical application of the literature aging B-K equation, the value of coefficients a and b will exceed the scope of [0，1], the exor e2xin B-K equation is modified as enx，and the improved equation is used to conduct data simulation. The results show that the improvement on B-K equation not only has reasonable significance, but also improves the accuracy of simulation, especially in solving the value range of coefficients a and b with weight significance in the B-K equation.

literature obsolescence; the B-K equation; the improved B-K equation

G350

A

1006-7302（2017）01-0014-06

2016-09-29

时秀娟（1981—），女，山东日照人，讲师，硕士，主要从事计算数学研究.