纤锌矿氧化锌纳米薄膜热导率的数值模拟研究*

白素媛，王立凡，支明蕾，王　斌，贾孟晗

(辽宁师范大学)

*辽宁省自然科学基金(2015020079)

0　引言

半导体材料是电子信息技术发展的基础，是人们一直研究、关注的焦点.伴随着第一代、第二代、第三代半导体技术的快速发展，半导体器件的尺寸已经进入到了微米、纳米尺度.又由于物质的局限性、量子效应、巨大的表面及界面效应，使微米、纳米尺度下的器件的热物性产生了明显的尺寸效应，因此器件的热学性质也开始受到了人们的广泛关注.由于薄膜材料的热导率会直接影响微纳米器件的散热性能,进而会间接影响器件的运行速度.因此,提高薄膜材料的热导率[1],使微纳米器件始终在最佳的温度下运行则是半导体电子工业要解决的一个难题. 在微尺度传热的领域中，数值模拟发挥着很大的作用，它可以对实验过程中遇到的不足之处进行弥补.数值模拟方法有很多种，其中应用最广泛的为分子动力学模拟方法(MD).王亚辉[2]、孙宪仁[3]、 Kato R[4]等均运用分子动力学方法分别对金刚石薄膜、单晶碳和锗薄膜、二氧化硅薄膜的热导率进行了研究.氧化锌[5]作为一种过渡金属氧化物，具有良好的光电磁等特性.与其它半导体相比，其制作工艺简单、成本较低、无毒、化学性质稳定、热稳定性好.在温度为500℃以下就可以制备出氧化锌薄膜，这比制备其他半导体材料所需要的温度都要要低，这也是氧化锌成为研究热点的原因.氧化锌晶体结构随着环境的改变会形成不同结构的晶体，分别为立方闪锌矿结构、立方岩盐结构、六边纤锌矿结构，其中纤锌矿结构最为常见，并且其热力学性质最为稳定性，因此纤锌矿型氧化锌成为研究热点.对于研究薄膜材料的热物性，热导率的大小将直接影响器件的耐高温性能以及器件的散热性能，所以，热导率的优化和求解具有重要的实际意义和研究价值.黄正兴[6]利用实验方法研究了六角纤锌结构氧化锌薄膜厚度对热导率的影响；Kulkami、Zhou[7]等利用分子动力学方法模拟氧化锌纳米带沿z方向上的热导率，研究结果显示氧化锌纳米带具有明显的温度效应和尺寸效应；杨平[8]等利用非平衡分子动力学方法对闪锌结构氧化锌薄膜界面的热导率进行了模拟，结果显示氧化锌薄膜界面的热导率随厚度的增加而增加.该文采用的是非平衡分子动力学方法对纤锌矿型氧化锌薄膜的热导率进行了模拟，并且分析了纤锌矿型氧化锌薄膜的厚度对热导率的影响.

1　分子动力学方法

分子动力学方法是根据经典牛顿运动学原理、应用力场的变化所发展起来的一种研究凝聚态物质的模拟方法. 非平衡分子动力学方法、平衡分子动力学方法是分子动力学的两种方法.平衡分子动力学方法(EMD)是应用线性相应理论和涨落耗散理论，运用相关函数求得热导率.所以，这种方法的优点是尺寸效应很小.非平衡分子动力学方法(NEMD)[9-10]是通过对系统施加相应的温度梯度或者施加相应的热流，根据傅里叶热导率定律求得热导率.该方法的主要的优点是计算速度快，缺点是具有显著地尺寸效应.该文研究的纤锌矿氧化锌薄膜的厚度在15.593～31.2096nm范围内，其模拟的结果与实验值相比具有明显的尺寸效应，因此该文采用非平衡分子动力学模拟方法进行研究.

在模拟过程中，根据热流形成的原因，采用非平衡分子动力学中的交换速度法进行模拟.交换速度法是通过交换粒子的速度来实现外加热流，即先给定热流，再统计温度梯度，最后利用傅立叶定律计算求得热导率，其计算公式为：

(1)

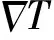
(2)

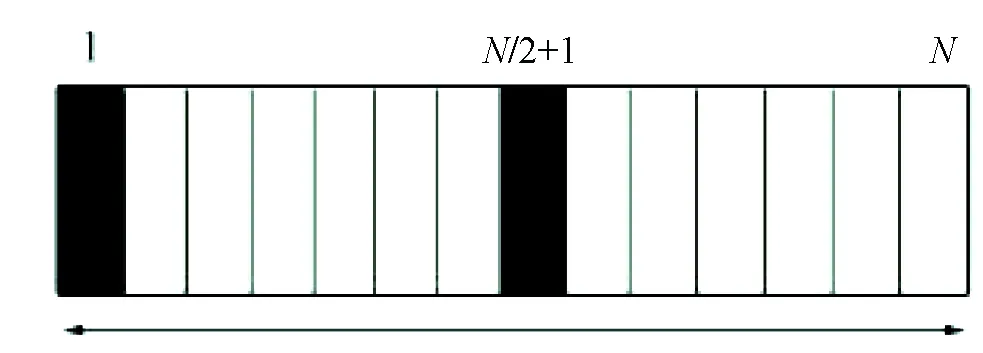
图1　非平衡模拟过程

其中，nk为第k层所含的原子数，kB为玻尔兹曼常数，mi为原子质量，vi表示原子速度.在图1中，将第1层规定为冷层，第N/2+1层规定为热层，并且符合周期性边界条件.粒子速度不断的交换将会引起热层更热、冷层更冷以及冷热层的温差会导致系统产生一个与热流施加方向相反的热量，从而产生温度梯度.当两个方向相反的能量在传递过程中达到动态平衡时，就会得到稳定的温度梯度响应曲线，同时通过原子之间的速度交换，可以计算外部施加的热流，也就是在整个速度交换过程中所传递的能量，从而体系的热导率可以结合(3)式得出：

(3)

其中，t表示模拟过程中粒子交换速率的总时间，A表示模型的横截面积，vh表示冷层中能量最高粒子的速率，vc表示热层中能量最低粒子的速率.由于周期性边界条件对热流方向有影响，体系内的热量将会从热层沿着两端流向冷层，所以，分母除以2.

2　模拟方法

2.1　系综

在分子动力学模拟方法中，对温度和压力的控制是运用系综的核心问题，该文选用微正则系综(NVE).在模拟过程中，体系粒子的数目保持不变，粒子的体积保持不变，体系粒子间的能量保持守恒，在体系演化过程中，粒子是沿着相空间中的恒定能量轨道进行演化.并且，在整个模拟过程中整个体系内的能量会一直不变，因此不需要重新控制体系的能量在模拟计算中首先将系统调节到特定的能量，同时给出初始温度，然后再进行调整，最后直到体系的能量达到指定的能量值.微正则系综(NVE)中，一般通过对温度的标定来实现对能量的调整.

2.2　作用势

在分子动力学(MD)模拟中，用势函数来描述分子之间、原子之间的相互作用力是动力学模拟的重要环节，势函数的选取会直接影响模拟结果的精确性.常用的势函数分为多体势和两体势.多体势主要为嵌入原子势；两体势主要有Morse势函数、Born-Mayer势函数、Lennard-Jones势函数、Buckingham势函数.该文采用Buckingham势函数来描述氧化锌薄膜内部原子之间的作用力，Buckingham势函数表达形式如下：

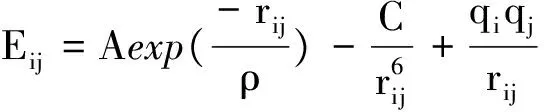
(4)

其中Eij表示原子i和原子j的相互作用能.

2.3　局域温度的量子修正

在分子动力学(MD)模拟中，由Boltzmann能量均分定理可以计算出系统的温度，其表达式如下：

(5)

其中N是模拟的粒子总数， kB是玻尔兹曼常数,TMD是系统模拟得到的温度，mi是粒子的质量，vi是粒子的速度.当体系的温度远低于材料的Debye温度时，由于体系的比热容与其温度有关，所以(5)式不再成立，也就是说系统实际的温度T≠TMD.为了得到精确的结果，务必对(5)式中的模拟温度TMD、模拟结果kMD进行量子化修正.采用Debye模型进行系统温度统计的量子修正，修正积分方程如下:

(6)

通过求解(6)式，可以得到和局域温度TJ,MD相对应的晶格温度Tj.该文选择的Debye模型为:

ω=vq

(7)

Debye模型所给出的晶格热容为:

(8)

其中Cv是质量定容热容，ΘD是Debye温度.在Debye近似下，能量方程(6)转化为:

(9)

该文通过求解方程(9)，实现了局域温度的量子修正.

3　结果与讨论

在半导体材料中，氧化锌是一种过渡金属氧化物、Ⅱ-Ⅵ 族宽禁带半导体材料，具有较高的激子结合能，其化学性质和热物性非常稳定，既可以工作在室温下，又可以工作在高温下，其制备温度比其它宽禁带半导体都要低. 由于在低维条件下，氧化锌的热流密度和电场强度都很大，所以其热物性变得尤其重要.氧化锌晶体结构[11]如图2所示，其参数分别为：禁带宽度大约为3.37eV、熔点为1975 ℃，晶胞参数a=3.289 Å，c=5.307 Å.该文采用的是非平衡分子动力学模拟方法，模拟系统在xy截面上采用4×4个晶胞，在z方向上取20、24、28、32、36、40个基本单元，系统温度为300K，系统的时间步为1.1fs，所模拟的计算步数为150万步.

图2　纤锌矿结构氧化锌晶体结构

以4×4×96系统，薄膜厚度为24.963nm为例，在经过150万步计算之后得到如图3所示的温度分布曲线，根据图像可以看出，各层的温度分布曲线比较光滑，黄色原点为高低控温层，由于热流将从控温层通过，所以控温区内存在温差.

图3　厚度为24.963 nm的氧化锌薄膜中各层温度分布情况

表1 为温度在300K时氧化锌薄膜的热导率的计算结果，由表可知，薄膜厚度在15.593～31.2096nm范围内的氧化锌薄膜，其热导率在0.87～1.52165W/(m·K)之间.图4给出了氧化锌薄膜热导率与厚度之间的关系.由图可知，当模拟的薄膜厚度在15.593～31.2096nm之间时，热导率随薄膜厚度的增加而增加，与大体积的氧化锌热导率相比，具有明显的尺寸效应.

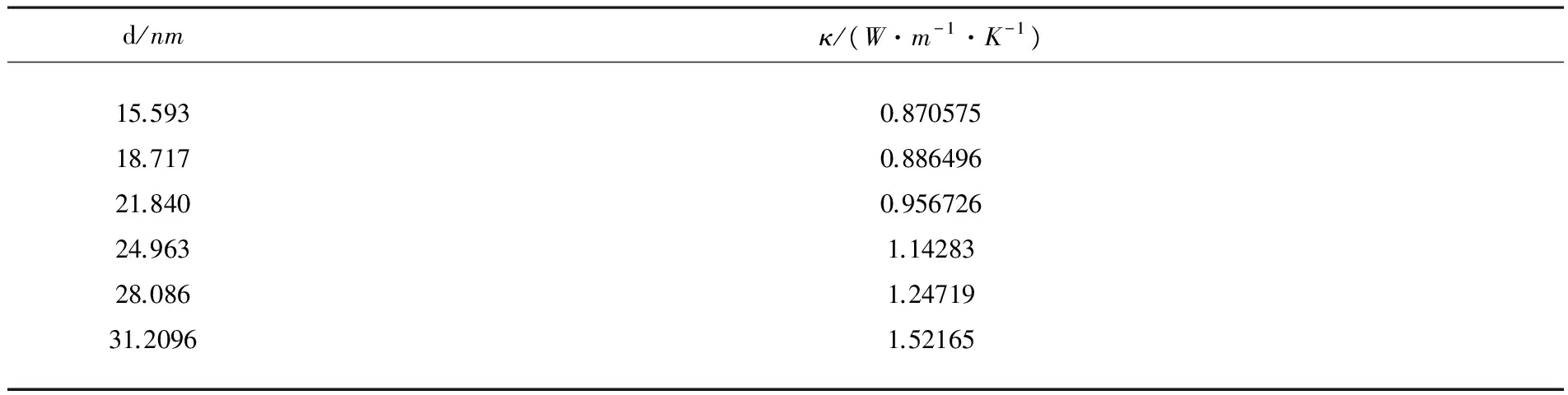
表1　氧化锌薄膜热导率的计算结果

在半导体材料中，热传导是通过声子之间的相互作用完成的，并且声子的运动决定了材料的传热特性.根据声子气的动力论[12]，热导率可以表示为：

(10)

其中，v表示声速，l表示声子的平均自由程.根据固体物理理论，当发生尺寸效应时薄膜的厚度必将小于其声子的平均自由程.根据该文所模拟的温度，可用下式近似表示其声子平均自由程：

(11)

其中， γ是Gruneisen常数，通常情况下γ≈2，Tm是材料的熔点温度，a是晶格常数.该文模拟的氧化锌材料，可以根据(11)式估算其平均声子自由程，并且其估算值要大于该文所模拟的薄膜厚度.所以，整个薄膜界面显示出尺寸效应.

另外，由于薄膜边界对声子的散射也会影响热导率的大小，因此，可以根据Matthiessn法则来确定薄膜中有效的声子平均弛豫时间，即：

(12)

其中， τb是弛豫时间， p是薄膜边界对声子的镜反射率，d是薄膜的厚度.根据(12)式以及晶格导热系数可以得出，当薄膜的厚度和薄膜边界对声子的镜发射率越大时，其有效弛豫时间也越大，从而薄膜的热导率也会越大，反之则越小.这就是薄膜的热导率随着薄膜的厚度增加而增大的原因.

文献[5]中运用实验方法，即通过组建瞬态热反射测试系统对采用溶胶凝胶法的氧化锌薄膜的热导率进行了测试.研究温度为500 K、薄膜厚度在80～276 nm之间，最后得出热导率的范围在1.4～6.51 W/(m·K)之间，研究结果表明热导率随氧化锌薄膜厚度的增加而增加.与该文所得到的结果相类似，可见该文的研究是可信的和合理的，至于还存在差异，是由于采用的方法不同而导致的.

4　结论

( 1)采用微正则系综，利用Buckingham势函数，运用非平衡分子动力学方法计算氧化锌薄膜的热导率.

(2)模拟温度为300K，模拟的氧化锌薄膜厚度在15.593～31.2096 nm之间，其热导率计算结果范围在0.870575～1.52165 W/(m·K).

(3)当系统温度一定时，氧化锌薄膜的热导率随着薄膜的厚度的增加而增加.

(4)用气动理论对研究结果进行分析，观察到氧化锌热导率的模拟结果具有明显的尺寸效应.

[1]Afshin Ahmadi Nadooshan. An experimental correlation approach for predicting thermal conductivity of water-EG based nanofluids of zinc oxide[J]. Physica E,2017,87:15-19.

[2]王亚辉，刘林华，孔宪仁.金刚石薄膜热导率的分子动力学模拟[J].哈尔滨工业大学学报，2006,38(5)：708-711.

[3]孔宪仁，吴国强，孙兆伟，等.单晶碳和锗薄膜热导率的分子动力学模拟[J].哈尔滨工业大学学报，2006,38(4)：517-519.

[4]Kato R. Conductivity Measurement of Thermally-Oxidized Si Films on Silicon Wafer Using a Thermo-Reflectance Technique[J].International Journal of Thermophysics,2005,26(1):179-190.

[5]宋淑芳.纳米ZnO薄膜的特性研究[D].内蒙古大学.

[6]黄正兴.薄膜热导率的测试与分子动力学模拟研究[D].大连理工大学.

[7]Ambarish J Kulkami, Zhou Min.Size-dependent thermal conductivity of zinc oxide nanobelts[J].APPLIED PHYSICS LETTERS,2006,88(14):19211-19213.

[8]杨平，吴勇胜，许海锋，等. 纳米薄膜界面热导率的分子动力学模拟[J].物理学报，2011,60(6)：066601(1-7).

[9]Wang Zhiguo, Gao Fei, Crocombette Jean-Paul. Thermal conductivity of GaN nanotubes simulated by nanequilibrium molecular dynamics[J].PHYSICAL REVEW B,2007,75(15):33031-33034.

[10] Yasushi Ichikawa,Yasuaki Hiwatari.Thermal conductivity of uranium dioxide by nonequilibrium molecular dynamics simulation[J].PHYSICAL REVIEW B,1991,60(1): 292-298.

[11] Chen Mingyuan, Hong Zhenghan, Lin Shiangjiun,et al. Buckling instability of zinc oxide nanobelts under uniaxial compression investigated using molecular dynamics[J]. Computational Materials Science,2014,85:217-222.

[12] Toru Yoshikawa,Takashi Yagi,Nobuto Oka,et al.Thermal Conductivity of Amorphous Indium-Gallium-Zinc Oxide Thin Films[J].Applied Physics Express,2013,6(2):11011-11013.