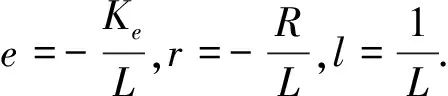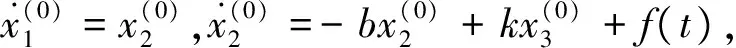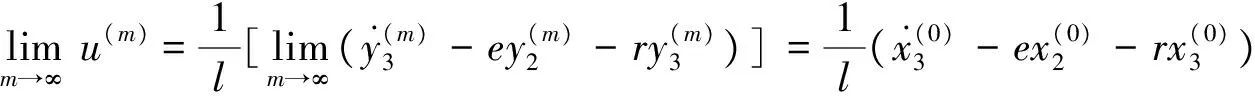一类直流电机系统的鲁棒稳定性与最优控制

王丽洁

(哈尔滨理工大学)

0　引言

对直流电机系统进行动态分析,根据系统的各参数的实际意义,建立数学模型,然后研究该系统的稳定性与最优控制问题,是近年来国内外学者对直流电机系统进行定性定量研究的一个重要方法.由于作用在电机上的未知摩擦、推力波动、耗损等不确定因素,使得对该领域的研究日趋复杂化,也因此该问题的研究日益成为人们研究的热点.文献[1,2]在直流电机系统的鲁棒控制问题的研究取得了一些结果.文献[3]研究了直流电机系统自适应补偿控制问题.文献[4]建立了直流无刷电机系统的数学模型,并研究其鲁棒控制问题.该文在文献[3,4]的基础上,将不同的扰动信号统一考虑,研究了直流无刷电机系统的鲁棒稳定性,得到了其闭环系统的一个鲁棒稳定性结果.此外,该文把扰动信号作为确定的时间函数信号,研究了系统对指令信号的跟踪问题.将直流电机系统中的位置控制电流作为控制变量,以范数作为性能指标函数来衡量对指令信号的跟踪精确度,得到了系统控制元的存在性结果.

1　系统的鲁棒稳定性

考虑直流无刷电机系

(1)

(2)

这里x1,x2,x3为状态变量,u为控制输入.将各项扰动统一记为Δ(x1,x2,x3),即

fd(t,x1,x2,v)]

(3)

对(3)的标称系统

(4)

选择控制器

u=Fx,F=(Lc1,Lc2+Ke,Lc3+R)

(5)

其中x=(x1,x2,x3)T,c1,c2,c3为待定系数.将控制器(5)代入(4)得闭环电机系统

(6)

取Lyapunow函数

则

要根据b,k的具体数值来确定c1,c2,c3使上式为负定.例如:当b,k满足

(3b+bk+2k-1)2-(b+1)(4bk+b(k-2)2+(b+2k-1)2]>0

(7)

时,取c1=-1,c2=b-1,则有

=(x1x2x3)×

(8 )

注意到实际物理意义b>0,k>0,由文献[5]的Schur引理,(8)式为负定的充要条件是

将上式整理为关于c3的二次不等式

(9)

当判别式,即(7)式成立时,上述(9)式有解c3,从而由Lyapunov定理知,标称系统(6)在平衡点是全局稳定的.

当电机系统中存在不确定性Δ(x1,x2,x3)时,即如系统方程(3)所述,则有

(10)

|Δ(x1,x2，x3)|≤ε(x1+2x2+x3)2,ε

(11)

那么可根据这个界函数,将控制器(5)进行适当的修正,仍能使闭环系统对于满足式(10)的Δ(x1,x2,x3)保持稳定,即具有鲁棒稳定性.例如,可修正控制器为

u=(-L(1+ε),L(b-1-3ε)+Ke,Lc3+R)

则按上面的推导方法,当条件

[3b+(b-ε)k+2k-1-ε]2-(b+1-ε)[4(b-ε)(k+ε)+(b-ε)(k-2)2+(b+2k-1-2ε)2]>0.

定理1直流电机系统(1),在其各项不确定扰动函数满足界条件(11)式时,是鲁棒稳定的.

2　系统的最优控制

当电机系统(3)中的Δ(x1,x2，x3)为一确定的扰动函数,即Δ(x1,x2,x3)=f(t)时,系统(3)式可化为

(12)

记I=[0,T],T>0,设L2(I)是I上Lebesgue平方可积函数构成的Hilber空间.内积和范数分别定义为

设N>0,记电机系统的控制集为

U={u∈L2(I)|0≤u(t)≤N,a.e.t∈I}

则不难看出U为L2(I)的闭凸子集,记Sobolev空间

W1,2(I)={x∈L2(I)×L2(I)×

在W1,2(I)中定义范数

由Sobolev嵌入定理,W1,2(I)可看成L2(I)×L2(I)×L2(I)中的完备子空间.

任取u∈U代入定解问题(12)中,系统方程(12)存在唯一的解x=(x1,x2,x3)T.设一指令信号为yr∈L2(I),定义指标泛函I为转子角跟踪yr之差的范数,即

J(x)=‖x1-yr‖,x=(x1,x2,x3)T

(13)

取集合W为

W={x∈W1,2(I)|存在u∈U,使得x是方程(12)的对应于u的解}

(14)

电机系统的最优控制问题就是寻求u0∈U,使与之对应的解x0∈W,满足

J(x0)=inf{J(x)|x∈W为对应于u的方程(12)的解，u∈U}

(15)

定理2设指令信号yr给定,则W是W1,2(I)上的闭凸集.

证明凸性.设x(1),x(2)∈W.由W定义可知存在u1,u2∈U,使得x(1),x(2)分别为定解问题(12)的相应于u1与u2的解,即

(16)

对任意0<τ<1,记x=τx(1)+(1-τ)x(2),u=τu1+(1-τ)u2,则易看出x∈W1,2(I),u∈U,且可算出

x2

ex2+rx3+lu

由于0≤ui≤N,i=1,2,易知0≤u≤N.从而u∈U,且x是对应于u的方程(12)的解,故x∈W.凸性证毕.

闭性.对任意的序列x(n)∈W,n=1,2,…,且

(17)

由W的定义知存在序列un∈U,n=1,2, …,使得x(n)为对应于un的定解问题(12)的解,即

(18)

由W1,2(I)中范数的定义知

由(18)第3式,并利用上式得

定理3设指令信号yr给定,则电机系统在U中存在最优控制元u0.

证明设x(n)∈W,n=1,2,…,是(15)式极小化序列,即

J(x(n+1))≤J(x(n)),n=1,2,…

(19)

(20)

记x(n)相对应U中的控制元为un,由解对参数函数的连续依赖性,当u在有界集U中取值时,W亦为有界集.由定理2,进而可知W为W1,2(I)中的有界闭凸集,故能从{x(n)}中选子列(不妨设其自身),使得

(21)

由Mazur定理,存在{x(n)}的凸组合序列

使得y(m)∈W,且

(22)

(23)

由(22)和(23)式得

(24)

结合(22),(24)式及范数函数J的连续性得

以上说明u0∈U是电机系统(12)的最优控制元.定理3证毕.

[1]刘雨,苏宝库,曾鸣.一种改善无刷自流电机驱动系统速率平稳性的鲁棒重复控制方法[J].中国电机工程学报,2005,25(10):144-148.

[2]孙宜标,闫峰,刘春芳.基于u理论的永磁直线同步电机鲁棒重复控制[J]. 中国电机工程学报,2009,29(30):52-57.

[3]沈陆娟,蔡建平.基于性能的直流电机系统未知推力波动的自适应补偿控制[J].数学的实践与认识,2013,43(1):141-147

[4]Yao Bin, Xu Li . Adaptive robust motion control of linear motors for precision manufacturing[J].Mechatronics,2002,12:595-616.

[5]梅生伟,申铁龙,刘康志.现代鲁棒控制理论与应用[M].北京：清华大学出版社,2008.