基于非参数估计的约化方法的信用违约互换定价*

欧阳峰，刘冠琦，王玉文

(哈尔滨师范大学)

*国家自然科学基金资助项目(11471091)

0　引言

信用违约互换是合同的卖出方给买入方提供的一种信用保险，是为了将经济实体的信用风险通过转移、重组和转换，从而规避信用风险的一种有效形式.信用风险通常被人们称为违约风险，是指当参考实体违约时对买入方经济造成损失的风险[1].在约化方法中，风险系数通常被用来描述违约，通过对风险系数建立模型，从而间接得到违约概率.这种方法在可能影响违约的因素和风险系数之间建立一种联系，因此有很强的适应性.Jarrow等[2]将违约概率的转移矩阵引入约化模型，其假设公司违约过程服从一个时间齐次的马尔科夫过程.Lando[3]对模型进一步扩展，其假设公司的违约过程服从 Cox 随机过程.Stephan4针对回收率为外生变量这个缺点，对其进行了改进，将回收率定义为违约率的联合随机函数.郭培栋[5]在约化方法下给出了一种随机波动率违约强度模型，并且分析了随机波动率对违约债券定价和利差的影响.陈正声，秦学志[6]提出了基于交易对手间违约行为相互影响的非线性环形违约强度模型的构建方法.该文考虑了约化方法下对含有扩散函数的风险系数的估计以及定价问题.

1　基础知识

定义1.1[7]{Γt}t≥0是一个风险过程，当且仅当Γt满足

P(τ>t|Φt)=e-Γt

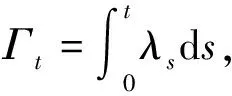
引理1.1[8]设λt是随机的且满足Vasicok模型，即dλ1=β(θ-λt)dt+σ(λt)dBt,则它的解为

其中β,θ为大于0的常数，σ(λt)是λt的扩散函数.且β,σ,θ为估计的重要参数.

2　建立模型

设信用违约互换的面值为1，合同到期日为T，保费是固定的并且在每年的年末支付一次，其中不含交易对手信用风险，以连续复利方式计算的无风险利率为rt，违约发生后参考实体债券的回收率为R，信用违约互换的价格为c.由无套利原理，买入方支付保费的现值和应该与卖出方赔付的现值相等，文献[9]给出了在约化方法下该信用违约互换的定价公式(1)：

由公式(1)可知，信用违约互换价格的决定性因素在于λt的确定.

在约化方法中，随机违约强度模型主要有两种形式：跳扩散模型和均值回归模型[5].该文采用具有均值回复特征的Vasicek模型来表示随机违约强度.

在引理1.1的Vasicek模型中，θ为λt的长期水平，β是回复到长期水平λt的速度.令Zt=θ-λt，则λt=θ-Zt，

dλt=d(θ-Zt)=βZtdt+σdBt

(2)

则Vasicek模型化为：

dZt=-βZtdt-σdBt

(3)

在Vasicek模型中，λt围绕其长期水平θ上下波动，利用全部违约强度历史数据的平均值估计长期违约强度θ则有

其次，讨论σ的估计.

对于扩散过程，无法直接观察到扩散系数σ本身，为了估计σ，先要构造σ2(Zi)的样本，由(3)式知需先通过测度变换，消去多余系数β.取

令

定义测度

然后，将dBt=dWt-μ(Zt)dt代入(3)式，得

(4)

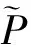
(5)

在(5)式中，记

(6)

将εti(i=0,…,n-1)记作随机误差序列，由It积分的性质可知：

(-σ(Zt))dWt]=0

引理2.2[11]设过程Zt满足微分方程

dZt=-σ(Zt)dWt，且设σ(·)满足线性增长条件、Lipschits条件以及Novikov条件，对r>1，

(7)

则存在常数k，使对r>2

证明见[11].

在(5)式中，如果记

则由(6)、(7),将(5)式表示为

(8)

式中，en(τ,ω)为系统误差.

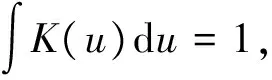
hn,T→0,

nhn,T→∞，则∀x∈D，有以下σ2(x)的局部多项式估计.事实上，有

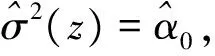
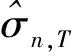
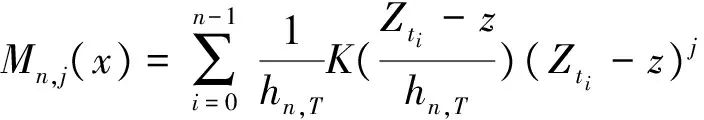
通过非参数估计以及参数估计的方法得出了参数β,θ,σ的估计，从而可以得出风险系数过程λt的估计.

因此，可通过λt的估计求得信用违约互换的价格.

非参数方法不局限于对总体分布的假定，具有广泛的适用性.当采用非参数方法对模型进行统计推断时，相应的信用违约互换定价问题就是信用违约互换的非参数定价.信用违约互换的非参数定价研究包括两个方面，一是构造适当的统计量，解出信用违约互换价格估计；二是必须考虑到漂移与扩散系数非参数估计量的误差对最终的信用违约互换价格估计将产生什么影响.只有了解这种影响，才能评估定价的精确性，并且可进一步通过比较理论估计价格与实际市场价格对信用违约互换定价模型进行统计检验.

[1]张新年.分级信用违约互换定价研究[J].哈尔滨师范大学自然科学学报,2016,32(4):25-29.

[2]Jarrow R,Lando D, Turnbull S.A Markov Model for the Term Structure of Credit Risk Spreads[J].Review of Financiel Studies,1997,10(2):481-523.

[3]Lando D. On Cox Processes and credit risky securities[J].Review of Derivatives Research,1998,2(3):99-120.

[4]Stephan.Pricing Credit Derivatives under Stochastic Recovery[J].Stochastic Models Bus,2010(26):254-276.

[5]郭培栋，陈启宏.在约化模型下具有随机波动率的可违约债券定价[J].统计与决策,2010(20):134-136.

[6]陈正声. 考虑交易对手风险的衍生产品定价方法[J].系统管理学报,2011，20(3):151-160.

[7]任学敏，姜礼尚，梁进.信用风险估值的数学模型与案例分析[M].北京:高等教育出版社，2014.7-9.

[8]肖庆宪.Ornstein-Uhlenbeck 过程的参数估计[J].应用概率统计，2005,21(1):1-8.

[9]赵士玲.基于约化模型的CDS定价研究[J].科技创业，2013(9):55-58.

[10] 王玉文，刘冠琦，王紫，等.随机金融数学引论[M].北京:科学出版社,2015.

[11] Chen P.Nonparametric estimation of the diffusion coefficient under the linear growth condition[J].南京大学数学半年刊，2005,22(2):292-298.

[12] 陈萍，冯予.连续时间金融模型的非参数统计分析[M].北京:科学出版社，2015..