基于Matlab的二维PIC/MCC模型的实现

王俊杰 郑锦华,2 魏新煦 吴 双 许 璐

（1. 郑州大学化工与能源学院热能系统节能技术与装备教育部工程研究中心，郑州 450001；2. 郑州瑞邦石油机械有限公司，郑州 450001）

基于Matlab的二维PIC/MCC模型的实现

王俊杰1郑锦华1,2魏新煦1吴 双1许 璐1

（1. 郑州大学化工与能源学院热能系统节能技术与装备教育部工程研究中心，郑州 450001；2. 郑州瑞邦石油机械有限公司，郑州 450001）

为了实现限定条件下气体放电的二维模拟，基于Matlab通过编程手段开发模拟程序,并用此模拟程序对直流低压条件下氩气的放电过程进行验证。对电子速度进行麦克斯韦初始化，并进行结果验证。提取50个时间步长内的电子数变化趋势，验证了氩气放电过程中电子崩的发生；并且通过100个时间步长结束时的电子位置分布，可以观察到阳极鞘层的产生；根据解泊松方程至200步和300步结果的对比研究，验证在本文的模拟条件下200步解泊松方程是足够的；对电子速度均方根处理，得到温度分布示意图，验证了直流氩气放电时阳极板附近温度高的实验现象。至此，基于Matlab开发的二维粒子/蒙特卡洛碰撞的耦合（PIC/MCC）程序，能够进行气体放电模拟。

Matlab；PIC/MCC；直流放电；数学模型；麦克斯韦分布

高电压绝缘气体放电模拟一直以来是电工学领域的热点，PIC/MCC模型是低压条件下常用的放电模型，该模型自20世纪50年代被南部等人提出，至今几十年被不断完善[1-2]。很多国内的研究者采用这种方法给电器技术领域带来了发展，如：湖南大学的汪沨教授采用PIC模型对10%～90%SF6/N2混合气体中绝缘子沿面放电特性进行研究[3]；上海交通大学的研究团队采用改进的MCC方法研究SF6和CO2混合气体电子崩的参数[4]；沈阳工业大学研究团队采用PIC方法对断路器短间隙气体放电过程进行模拟研究[5]。

气体放电数学模型有：流体模型即N-S模型也称宏观模型；粒子（PIC）模型也称微观模型；二者混合模型三种[6]。本文针对低压气体放电进行粒子（PIC）模拟，因为在低压条件下（＜10mtorr）流体模型并不适用[7]。本文首次采用Matlab编程的方式，实现二维PIC/MCC模型。并对氩气直流条件下的放电过程进行模拟验证。氩气是微电子器件表面处理的常用气体，并在各种放电条件下被研究。因此选择氩气作为验证气体。

Matlab具有直接面向矩阵的特点，决定其在粒子模型实现方面有很大的优势。Matlab程序简洁且易于理解，并且可以与其他汇编语言进行混合编程，解决编程问题手段多变[8]，故采用Matlab来实现PIC/MCC模型的程序开发。

二维放电模型与一维模拟[9]相比有以下不同：①二维模型需要考虑平板边界条件对放电过程的影响，而一维模型无需考虑；②二维模拟能够直观的反映出在放电过程中，电子与离子的运动情况和各个参数的变化；③对于二维模型而言，在相同条件下的粒子放电模拟，要达到同样的参数精度，网格数目是一维时的二次方倍，计算时间成倍的增加，工作效率降低[10]。

本文从离散玻尔兹曼方程、建立完善的二维数学模型，到程序流程建立以及编程实现，再到氩气放电验证等角度，来讨论直流气体放电过程中的粒子模拟，并将模拟结果与实验现象以及其他研究者所取得的相关模拟结果进行比较。

1 PIC/MCC模型的Matlab实现

对直流低压条件下氩气PIC/MCC放电模型的研究基于以下几点假设：①忽略电子运动形成的磁场；②忽略带电粒子间的库伦作用，即忽略库伦碰撞；③边界为良导体，电子到达表面会被吸收；④为了达到验证目的并减少工作量，采用矩形放电区域，网格为正方形网格。

图1为编程实现模型的计算流程图，先要给各个粒子赋初始值。（其中包括粒子所带电荷，粒子的位置，初始速度等）进入第一个循环，按照面积权重将粒子所带电荷分配到各自邻近的网格节点上。接下来将网格节点的带电荷与外电场进行耦合，解泊松方程，得到各个节点的电场强度。带电粒子在得到的新的电场的作用下运动，然后利用MCC方法处理离子之间的碰撞过程。最后判断是否结束，没有结束进入下一个时间步长，直到循环结束，并进行结果分析。

图1 Matlab实现模型的流程图

1.1 满足麦克斯韦初始速度分布的实现

按照前面提到的模拟流程，第一步要实现参数的初始化。在Ar气放电的开始阶段，粒子满足麦克斯韦速度分布，需要对粒子速度进行初始化即速度分布满足方程为

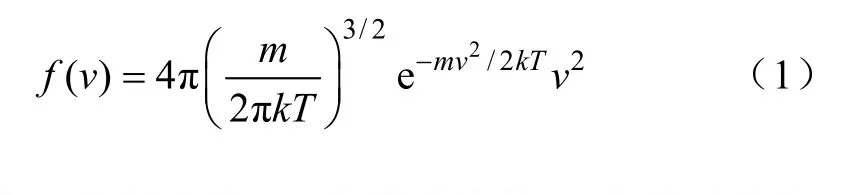
式中，T为气体温度；m为电子质量；v为粒子速度；k为玻尔兹曼常数。

图2 统计结果与麦克斯韦分布的比较

Matlab具有产生满足一定分布随机数的内部函数，例如：满足正态分布随机数的产生，平均分布随机数的产生等，但是没有产生满足麦克斯韦分布的随机数的函数。基于式（1）麦克斯韦分布函数，采用舍选法[11]，编程实现满足麦克斯韦分布函数的随机速度的生成，并编程对随机数进行验证，统计在模拟压力和温度的条件下，随机数的分布情况。对200个随机数的统计结果进行八次多项式拟合，图2中的拟合结果与麦克斯韦分布曲线一致，验证了编程的正确性，说明利用此方法，可以完成粒子速度大小的初始化。

1.2 玻尔兹曼方程离散之PIC部分

玻尔兹曼方程是气体动力学基本方程，PIC/MCC方法是基于玻尔兹曼离散方程的一种模拟方法。根据文献[1-2]玻尔兹曼方程可以离散为粒子部分和碰撞部分。其中粒子部分包括电荷分配模型、电场模型以及运动模型。碰撞部分用MCC模型进行研究。

在粒子赋予初值之后，利用权重函数（面积权重）进行二维电荷分配，实现电荷向网格节点的分配。图3为权重向节点分配的示意图，利用式（2）[1]计算节点A的面积权重。图3中（Xp,Yp）为粒子点的位置坐标，正方形单元网格的边长AB=Δh。与式（2）类似可以得到B、C、D点的权重式。

郜教授提出，乘的本质是缩放。读者可反复读“乘的本质是缩放”这一段，对乘法会有新的认识。张景中院士的文章也提出，现代数学中，并不一定从加法出发引入乘法，“几个几”的说法，不是数学语言，而是直观描述，从集合概念出发，建立乘法的概念。然而对于小学生来说，直观可描述建立乘法概念也是很好的，作为教师当然不应该只满足于这些，所以郜教授给我们提供的解读也是非常必要的，对于解读教材与教学设计应是有帮助的。郜教授的解读说明教师掌握本体性知识的重要性，提醒教师看教材要有一种居高临下的能力。

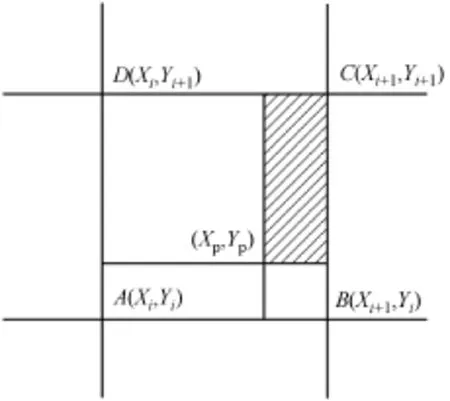
图3 面积权重分配示意图

根据网格节点的电荷密度，利用二维泊松方程实现电场求解，具体方法是有限差分法。方程的离散形式为

式中，ρi,j是网格节点（Xi,Yj）（任意节点）处的电荷密度。在泊松方程的求解过程中，每个步长内用200步就可以实现网格节点电势的求解（具体内容在本文第三部分论述）。由泊松方程解得网格节点的电势分布，电势向网格节点线性差值，可以实现节点电场强度的求解。在编程的过程中，需要注意边界线性差值公式与中间节点的区别。每一个时间步长求解泊松方程，会降低程序的运行效率，但根据相关文献，采取每一步长内对方程求解，能提高方程的收敛性。

解泊松方程得到网格节点电场的分布，带电粒子在极板电场和带电粒子的耦合电场作用下运动。运动方程的离散为

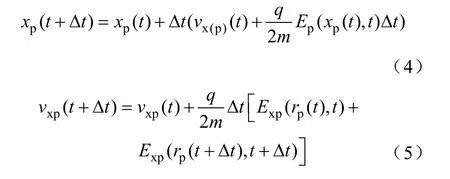
式（4）、式（5）分别是位移和速度在x方向上的离散，而y方向以及vy,vz的求解，与x方向类似，其中p代表第p个粒子。这里是耦合电场，在计算vx时需要通过解得新一个步长的电场分布，新一个步长的电场的求解需通过式（4）计算出新的粒子位置，进而算出t+Δt时刻电场的大小，再利用式（5），得到新时间步长下的速度分布。这样便实现了电场与运动方程的耦合。

1.3 玻尔兹曼方程离散之MCC模型

气体在放电的过程中，离子会发生剧烈的碰撞。碰撞形式有：离子或电子与分子间的弹性碰撞、电荷交换碰撞、电离碰撞、激发碰撞等。在电场中，发生何种形式的碰撞可以用MCC方法进行判断。MCC模型假设碰撞发生在一个时间步长的结束时刻，这样对于编程是可以实现的。对粒子先后用PIC和MCC模型处理，便实现了粒子模型与碰撞模型的耦合[1-2,12-13]。在利用Matlab编程的过程中需注意碰撞过程中电子的消失与出现的问题，可以利用Matlab提供的空函数和赋值函数来实现。

MCC模型在一个时间步长内，一个粒子最多只能处理一次碰撞，这就需要考虑时间步长的选取不能太大。参考birdsall提出的方法[1,12]，选取时间步长Dt=10-8s。

在放电过程中发生碰撞的概率，采用以下式确定：

式中，n为粒子密度；v为速度；ε为电子能量；σi为总碰撞截面，是各种类型的碰撞截面的总和。碰撞截面是与能量有关的量，随着粒子能量的变化而变化。意味着，粒子在不同时刻，所具有的总能量不同，决定发生碰撞的概率不同。

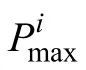
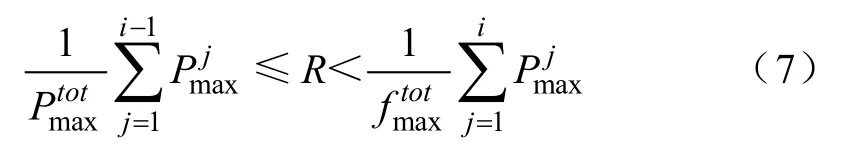
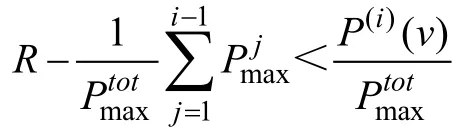
根据动量和能量守恒定律，中子和电子碰撞前的速度分别为V, v，碰撞后的速度分别为V', v'。当处理电子与中性粒子发生碰撞时，假设M+m≈M，V'≈V，即二者质量不在同一数量级，忽略中性粒子碰撞前后的速度差。电子碰撞后的速度可由下式计算得到[12-13]：

式中，h为笛卡尔分量；χ为散射角。散射角的计算用各项同性散射假设，参考式cosχ=1-2R2，R2为[0, 1]之间的随机数。关于散射角的处理可以参考其他论文的方法[1-2]。

2 模拟条件与结果分析

模拟条件：上表面加100V的直流电压，极间距为1mm，极板宽度为1mm；初始粒子权重为1010；气体压力：1Pa；初始时刻温度：300K。其余3个壁面接地，进行模拟。

模拟氩气放电过程，只考虑电子与中性粒子之间的弹性碰撞、电离碰撞和激发碰撞。经过100个时间步长之后，得到如图4所示的电子图4（a）和离子图4（b）位置分布，与实拍实验照片图4（c）对比。由图可以看到，在阳极附近区域有很多电子积累，电子的密度也呈现有一定规律的不均匀分布。

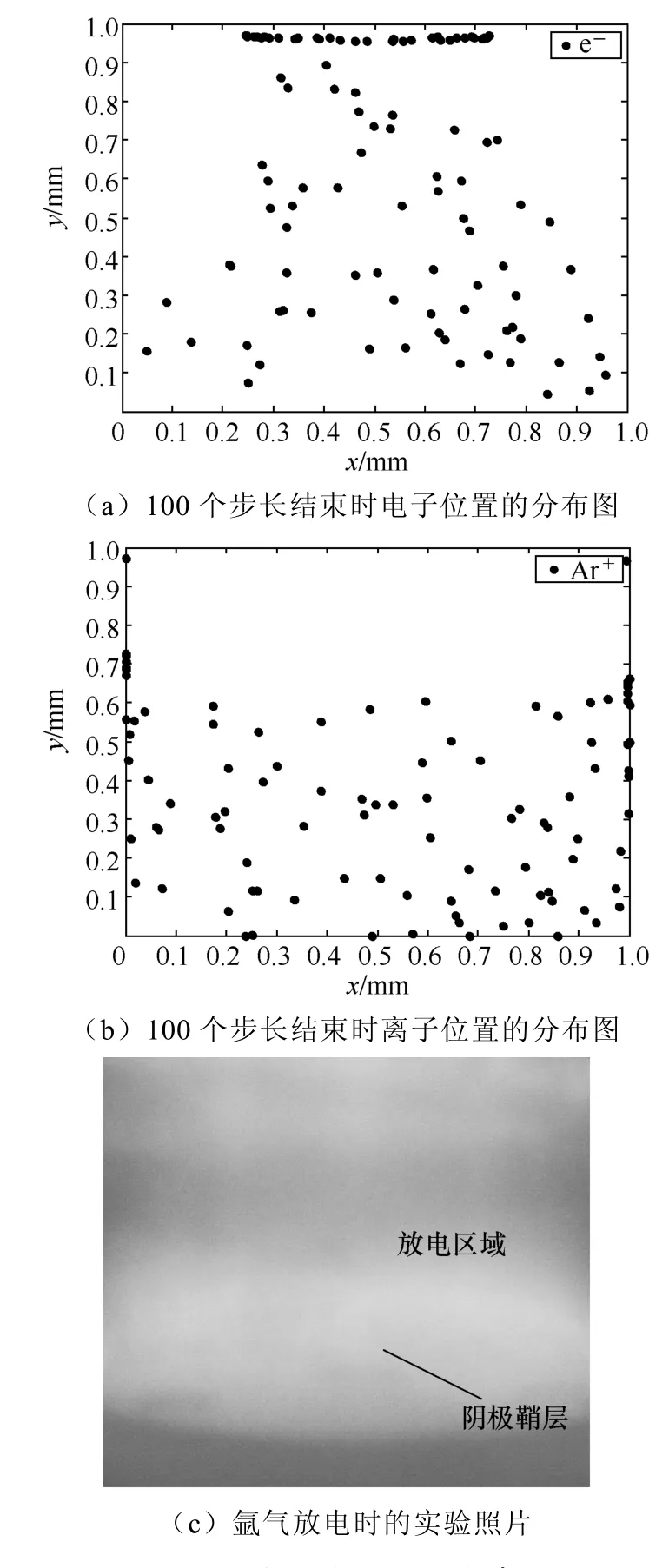
图4 氩气放电过程模拟

图4（a）为电子的位置分布，可以看到明显的阳极鞘层的形成。在放电初始阶段，由于电子的质量比离子质量小的多，在电场的作用下，高速向阳极运动被阳极大量吸收。离子的滞后性，会在电场停留积累。随着时间的推移，电子被吸收的越多，留下的正离子也越多，这时离子与阴极板形成的电场会中和掉一部分的极板电场，在放电区域与阴极板间会形成电压梯度很大的鞘层区域，称为阴极鞘层。由于离子运动速度比电子慢的多，甚至会在阳极附近出现离子正电势大于基板正电势的情况，这样便在阳极附近形成与阴极类似的区域，称为阳极鞘层，与图4（c）比较，可以看出电子分布与实验图片吻合。

图4（b）为离子的位置分布。经过一段时间的运动，离子被阴极吸附。由于阴极鞘层的作用，阳极会发生二次电子发射，来维持等离子体区域的电子平衡，这是等离子体形成的重要过程。本文模拟没有考虑二次电子发射的影响，这是模型需要改进的地方。实验照片图4（c）中，可以明显看出阴极板上方有很明亮的放电区域，即为阴极鞘层。此现象与图4（b）中离子分布的结果一致。

在二维模拟电子和离子分布的情况下，受边界0电荷条件的限制，电场分布并不是理想的直线分布。分布在不同位置的电子所受到的电场力是不同的。速度和位置的不同，决定粒子能量不同，发生碰撞的概率也不相同。因此二维模拟相比与一维更能反映真实电场中的情况。

取模拟步长的前50步，得到模拟电子数在前50个步长中的变化趋势，如图5所示。模拟区域中电子数目是反映放电激烈程度的主要参数。

在模拟开始阶段电子数目有一些波动，这是电子运动到阳极板和粒子电离出电子的双重作用的结果。在模拟进行到一段时间后，由于阴极附近离子的增加，被阴极吸收的电子数将显著减少，这时原子电离占主要作用，电子数目迅速增加。此结果与相关论文[9]中的模拟结果是一致的。

图5 电子数随时间步长的变化曲线

根据步长结束时电势分布图（如图6所示），可以看出，电势分布在二维区域中的分布是光滑的曲面。与300个循环的结果对比发现，200个循环解本模型中的泊松方程是足够的。并且能够明显地看到边界电势与中间部位的电势分布趋势是不一样的。中间区域变化较平滑，即电场强度比较接近。而在放电区域边缘，电势变化较剧烈，即场强变化较大。再一次验证了二维模拟与一维模拟是有显著区别的，故不能忽略二维边界条件对放电过程的影响。

图6 步长结束时电势分布图

对速度均方根处理，得到50个时间步长结束时，速度的对数分布示意图如图7所示。由于速度与温度的正相关性，速度分布可以反映出温度分布。由图可以看出在距离阳极板0.4mm左右，横向中间的位置，半径为0.13mm的区域内温度最高，电子

图7 速度的对数（温度）分布

运动速度最快，放电最激烈。所以阳极板容易受到周围放电反应的影响。此结果与氩气放电反应的实验相吻合，也验证了模型的正确性。

3 结论

本文基于Matlab编程实现了二维气体放电的PIC/MCC模型，并对直流低压条件下氩气放电过程进行了模拟验证：①编程实现麦克斯韦随机速度分布，实现粒子速度的初始化。其次，通过观察100个时间步长后的二维电子与离子位置分布图，可以看到阳极鞘层的形成，此现象与实际氩气放电过程相符。模拟过程考虑了边界条件对模型的影响，相较与一维模拟，该方法更接近真是的实验条件；②比较200个循环结束时的电势分布与300个循环时的泊松方程的解，证明泊松方程200个循环的求解是足够的。从此，根据模拟结果50个时间步长结束时超电子数达到110，并有直线增加的趋势，可以说明电子崩的发生。最后，根据温度分布示意图可以得到温度最高区域在阳极附近，此结果与气体放电实验相吻合。至此，可以证明通过Matlab编程基本实现了PIC/MCC模型。

[1] Birdsall C K. Particle-in-Cell Charged-Particle simulations, plus Monte Carlo collision with neutral atoms, PIC-MCC[J]. IEEE Trans.Plasma Sci, 1991, 19(2): 65-85.

[2] Nanbu K. Probability theory of electron-molecule, ion-molecule, molecule-molecule, and coulomb collisions for particle modeling of materials processing plasma and gases[J]. IEEE Trans. on Plasma Science, 2000, 28(3): 971-989.

[3] 汪沨, 肖晓林, 张宪标, 等. 基于PIC法SF6/N2混合气体中绝缘子沿面放电特性研究[J]. 电工技术学报, 2011, 26(8): 220-226.

[4] 吴变桃, 肖登明. 用改进的蒙特卡罗法模拟SF6和CO2混合气体电子崩参数[J]. 电工技术学报, 2007, 22(1): 13-16.

[5] 李静, 曹云东, 王尔智, 等. 断路器短间隙气体击穿过程的粒子模拟[J]. 中国电机工程学报, 2010(16): 125-130.

[6] 汪沨, 李锰, 潘雄峰, 等. 基于FEM-FCT算法的SF6/N2混合气体中棒-板间隙电晕放电特性的仿真研究[J]. 电工技术学报, 2013, 28(9): 261-267.

[7] 冯明, 张鉴, 黄庆安. ICP刻蚀中等离子体分布的模拟[J]. 电子器件, 2006, 28(3): 529-531.

[8] 张志涌. MATLAB教程[M]. 5版. 北京: 北京航空航天大学出版社, 2003.

[9] 李静, 曹云东, 邹积岩, 等. 直流气体放电过程中的离子分子碰撞模型[J]. 高电压技术, 2009(7): 1677-1682.

[10] 邵福球. 等离子体离子模拟[M]. 北京: 科学出版社, 2002.

[11] 刘沛华, 鲁华祥, 龚国良, 等. 基于FPGA的高速任意分布伪随机数发生器[J]. 应用科学学报, 2012, 30(3): 306-310.

[12] Nanbu K. Particle modeling of nonequilibrium plasmas and gases for materials processing[J]. Vacuum Science Technology, 2004(5): 1-57.

[13] Birdsall C K. Plasma physics via computer simulation[M]. New York: McGraw-Hill, 1985.

Realization of Two-Dimensional PIC/MCC Model based on Matlab

Wang Junjie1Zheng Jinhua1,2Wei Xinxu1Wu Shuang1Xu Lu1
(1. Engineering Research Center of Energy-saving Technology & Equipment of Thermal Energy System, Ministry of Education, School of Chemical Engineering and Energy, Zhengzhou University, Zhengzhou 450001;
2. Zhengzhou Reborn Petroleum Machinery Co., Ltd, Zhengzhou 450001)

In order to achieve the two-dimensional simulation of gas discharge under limited conditions, a simulation program based on Matlab has been developed in the paper, and utilized to verify the discharge process of argon under direct current and low pressure. Electronic speed was initialized through Maxwell equations and the results were verified. The occurrence of electron avalanche in the process of argon discharge was verified by extracting the change trend of the number of electrons in the 50 time steps, and the production of anode sheath was observed through the distribution of electron position at the end of the 100 time step. According to the solution of Poisson’s equation to the 200 step and 300 step, the solution of Poisson's equation in the 200 step was sufficient under the simulated conditions in this paper. The diagram of temperature distribution given by the root mean square treatments of the electron velocity successfully verified the experimental phenomena that the temperature near the anode plate was higher in the DC argon discharge. Thus, the two-dimensional PIC/MCC program based on Matlab can satisfactorily simulate the gas discharge.

Matlab; PIC/MCC; DC discharge; mathematical model; maxwell distribution

王俊杰（1992-），男，硕士研究生，研究方向为等离子体放电的模拟研究。