交直流系统离散无功优化精确化方法的研究

张 昕 章慧芸

（国网嘉兴供电公司，浙江 嘉兴 314033）

交直流系统离散无功优化精确化方法的研究

张 昕 章慧芸

（国网嘉兴供电公司，浙江 嘉兴 314033）

高压直流输电近年来在大容量电能传输中得到广泛的运用，其在经济性和运行特性方面有着突出的优点，利用交直流混联系统在各区域电网之间互联成为一种重要的输电方式。交直流系统的最优潮流（optimal power flow，OPF）特别是无功优化是系统的一个重要的研究方向，解决无功优化问题中的离散变量的优化问题一直是计算中的一个难点。本文以交直流系统的节点功率平衡方程和直流网络方程为基础，结合无功优化的理论，设计出一种解决离散变量问题的内点算法，以系统网损最小为目标函数进行无功优化计算，通过两个算例，验证了该算法解决交直流系统无功优化中离散变量优化的可行性。

交直流系统；内点法；无功优化；离散变量

高压直流输电（HVDC）有着许多优点：线路造价低，杆塔结构简单，线路走廊窄，功率和能量损耗小，控制方式灵活等[1-6]，同时直流线路运行时无电容电流，其功率和电流的调节控制比较容易并且迅速，可以实现各种调节、控制，因此构架交直流并列运行系统可以弥补纯交流系统的一些不足。鉴于上述原因，高压直流输电现已逐步在电网大容量电能传输中普及，嘉兴供电公司也承载着4条跨区直流输电线路的属地运维工作，分别是±800kV复奉线、±500kV葛南线、±500kV林枫线和±500kV宜华线[7-10]。

目前，对含HVDC的交直流混合系统（下称交直流系统）的潮流计算、最优潮流（optimal power flow，OPF）的研究日益增多，本文着重研究了交直流系统OPF中的一个重要分支-无功优化。交直流系统无功优化问题是一个复杂的非线性整数规划问题，其控制变量中同时包含了连续变量和离散变量。文献[11]中提出了交直流系统的OPF计算模型，文献[12]提出了交直流系统的序列二次规划法解决方案。文献[13]中将交直流系统OPF模型用于可用输电能力的计算。文献[14]中将交直流系统OPF模型用于无功优化配置方案的计算，但是上述文献均没有考虑离散变量的特性，以优化连续变量的思路来处理离散变量，导致虽然按照计算可以得到理论上的最优解，但实际系统中离散变量，如变压器变比、无功补偿量无法达到计算中各自变量的最优解，因此必须对离散变量进行离散化处理。本文基于内点算法，设计一种可对离散变量进行优化的方法，并通过算例进行了验证。

1 交直流系统的数学模型

1.1 交直流系统的稳态模型

简单的直流输电系统基本原理接线图主要包括两个换流站C1、C2和直流线路，如图1所示。

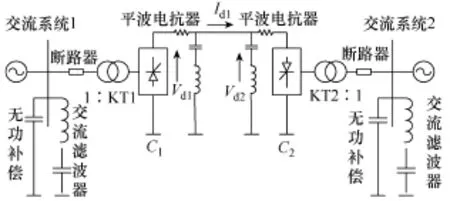
图1 直流输电的基本原理图

当计算交直流系统时，其描述全系统的非线性代数方程中不仅需要包含交流系统变量，同时也要包含直流系统变量。

纯交流节点的节点功率方程为

直流节点的功率方程为

换流器的稳态方程为

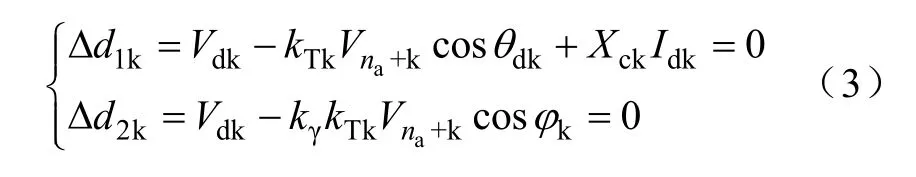
直流网络方程为

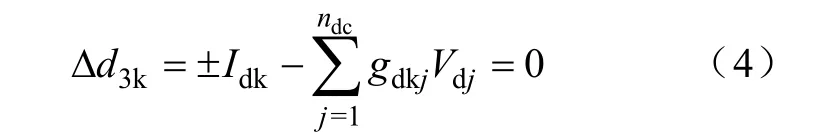
直流输电控制方程为

上述计算式构成了标幺值下交直流系统的稳态等式约束模型。

1.2 直流稳态控制方式

在直流输电系统中可以通过调整换流器的控制角及换流变压器的变比来控制直流线路输送的功率，直流线路两端的交流系统电压对直流线路的输送功率也产生直接影响。

一般交直流系统考虑以下几种控制方式：定电流控制、定电压控制、定功率控制、定控制角控制、定变比控制。控制方式可以自由组合，本文对直流线路换流器采用以下控制方式。

方式1：整流器为定功率控制及定控制角控制，逆变器为定电压控制及定控制角控制，记为OPF1。

方式2：整流器为定功率控制及定控制角控制，逆变器为定电流控制及定控制角控制，记为OPF2。

2 基于内点法的交直流系统精确连续方法的无功优化

2.1 原对偶内点法

内对于一般的计算模型，可以简化为以下非线性优化模型[15]，即

将不等式约束转化为等式约束，以及将目标函数改造为障碍函数后，可得到该问题的拉格朗日方程，即

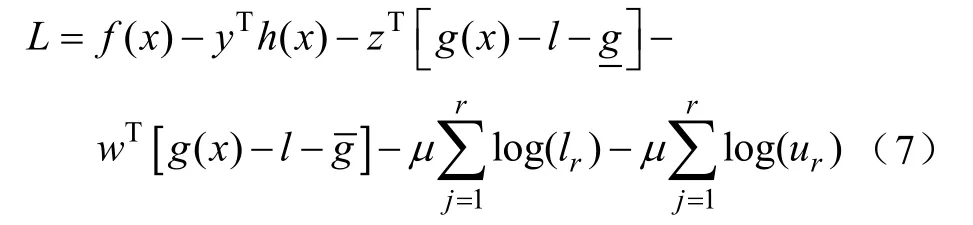
使用拉格朗日乘子法求解上述问题，得到求解方程组为

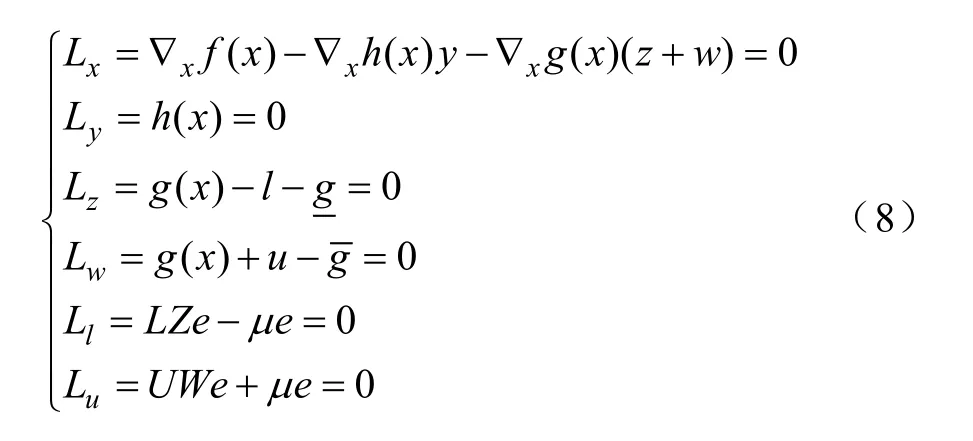
该方程组极值的必要条件是一个非线性方程组，采用牛顿法求解，变换后的求解方程组为

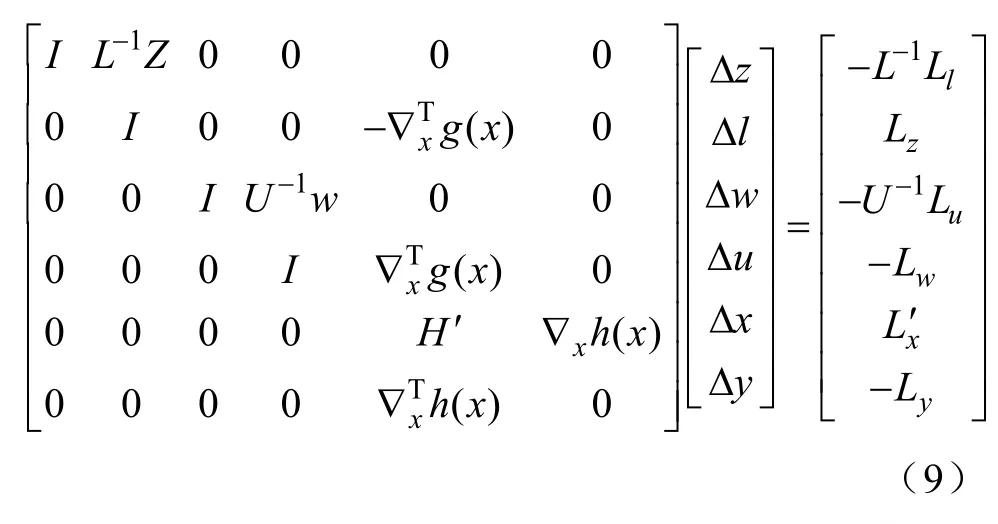
通过修正值的不断迭代求解，最后达到系统的最优运行方式。

2.2 含离散惩罚函数内点法的交直流系统的无功优化

为交直流系统的无功优化方程变量为

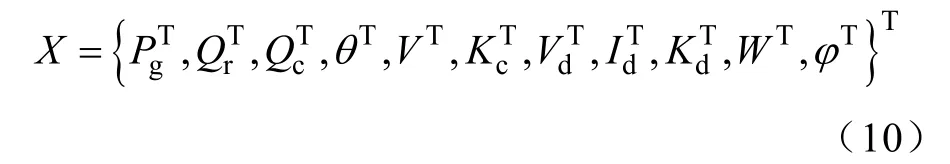
目标函数为系统网损最小，即

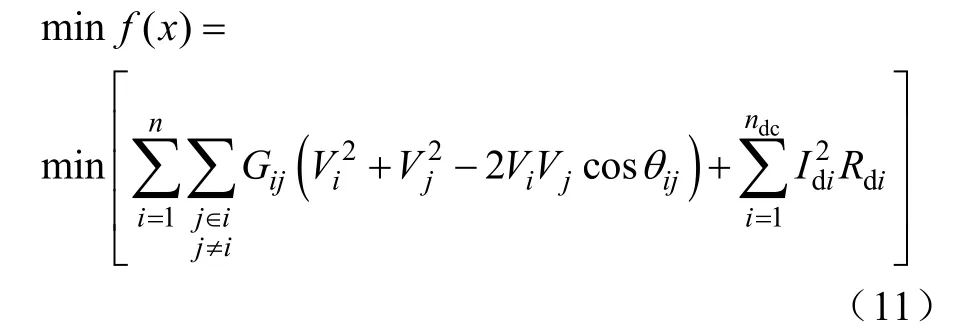
由对交直流系统的变量分析可知，可投切电容器的无功出力向量Qc和有载调压变压器的变比向量Kc具有离散性，本文对其进行类似不等式约束的处理，使用一个正曲率的二次罚函数来模拟离散变量所引起的虚拟消费，并把这个二次罚函数增广到拉格朗日函数中，使用该方法后，可以使离散变量继续受到全局优化的影响[16]。

令二次罚函数为φ(x)，离散变量按均匀的分级步长变化，则定义离散变量x的领域O(x)为如下区间：

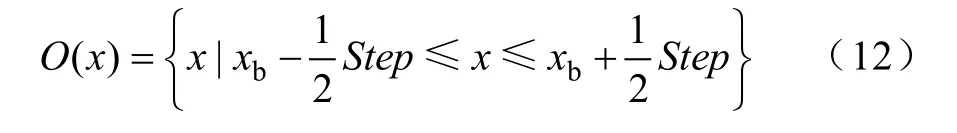
式中，Step是离散变量x的分级步长；xb为离散变量的领域中心，当x处于上述领域时，应使得其向领域中心逼近，可以得到该罚函数的一般形式：

式中，vb为正数罚因子。这里需要注意的是，领域中心在优化过程中是不断变化的，根据离散变量实际计算的值求出最靠近的离散分级值获得。

将该罚函数增广到拉格朗日函数中：

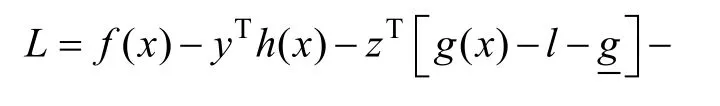
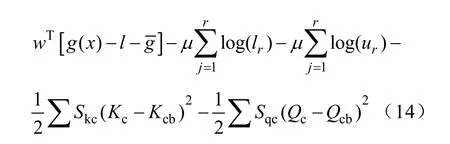
拉格朗日乘子法的方程组变为

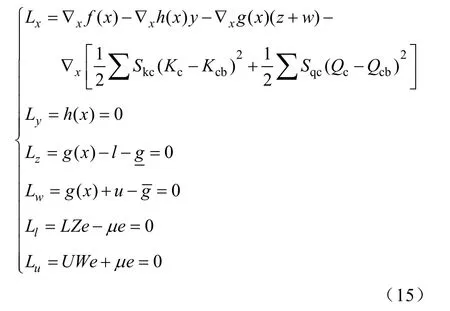
按照牛顿法迭代求解，即可得到该方程的近似解。

2.3 离散惩罚函数的引入机制

在二次罚函数中，对其效果起直接影响作用的是罚函数的引入时机以及罚因子的大小。

若罚函数引入时机较早，则其会干扰系统的全局优化，其领域中心会频繁的变动，导致优化时间变长，优化效果不理想；若引入时机较晚，则可能会导致罚函数的惩罚机制不够理想，延缓计算的收敛。由于对偶间隙Gap可以反映计算的收敛情况，当Gap小于一定的值时，不等式约束基本确定，此时引入罚函数时机较适当，故本文引入罚函数的时机为Gap＜0.1，且无功补偿迭代量小于其1/2步长，变压器变比迭代量小于其1/4步长。

罚因子的功能是增强离散变量向领域中心靠拢作用，当离散变量向领域中心逼近时，罚因子的值要不断的增大。电容器罚因子的初始取值可定为50，变压器变比罚因子的初始取值可定为500[17]。同时，当离散变量的迭代值小于其1/4步长且罚因子小于5×107时，需要增大罚因子来增强向领域中心逼近能力，此时罚因子扩大十倍。

3 算例分析

3.1 IEEE-5节点算例

将IEEE-5节点3、4间支路改造为直流线路，并在节点1处加装无功补偿装置，如图2所示。

直流系统初始参数见表1，其中除了相位ϕ 有单位（°）之外，其他变量均为标幺值。无功补偿量上下限分别为4.0和0，步长为0.05；变压器变比上下限分别为1.1和0.9，步长为0.0125。

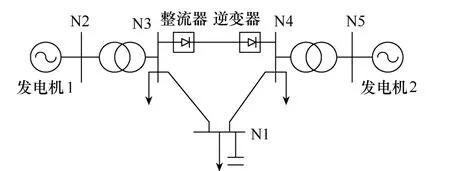
图2 IEEE-5节点系统结构图

表1 IEEE-5直流系统参数值

算例中的换流器以不同的控制方式组合，计算的结果见表2。

表2 各种控制方式下含离散变量交直流系统无功优化后系统参数情况

3.2 IEEE-30节点算例

对于IEEE-30节点系统，将节点2、4间支路改造为直流线路，并在节点21、30节点处加装无功补偿装置，系统的结构图如图3所示。

图3 IEEE-30节点系统结构图

直流系统初始参数见表3。无功补偿量上下限分别为4.0和0，步长为0.05；变压器变比上下限分别为1.1和0.9，步长为0.0125。

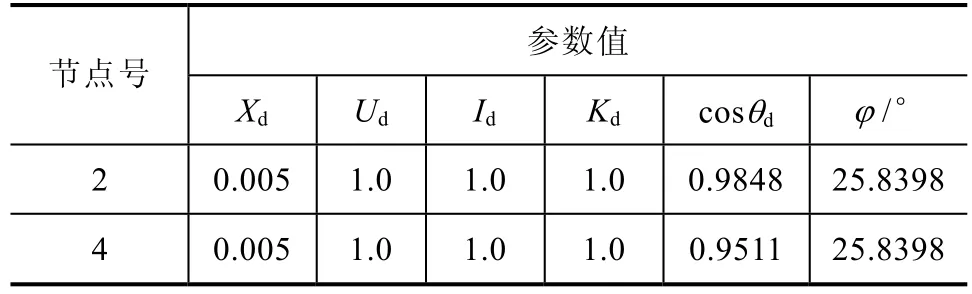
表3 IEEE-30直流系统参数值

通过计算不同控制方式的收敛曲线及相关变量对比如图4、图5和表4至表6所示。

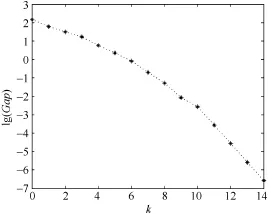
图4 交直流系统控制方式1的收敛曲线

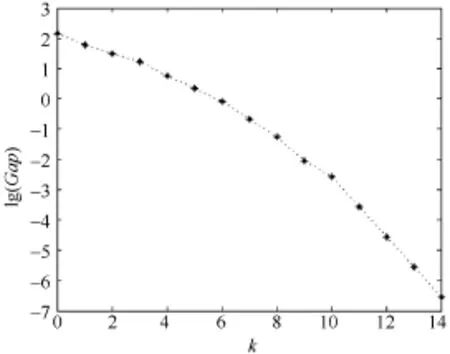
图5 交直流系统控制方式2的收敛曲线

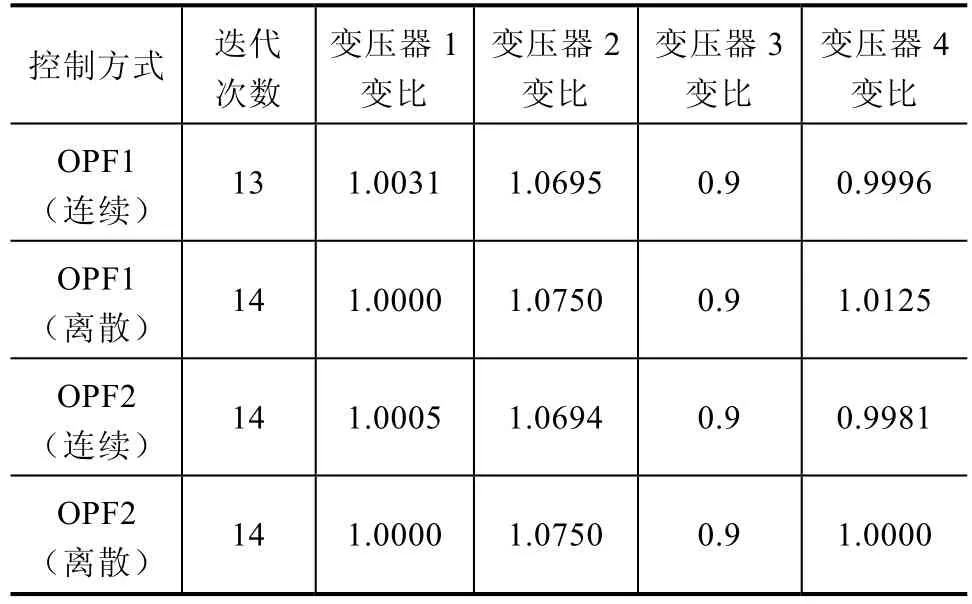
表4 各种控制方式下交直流系统的迭代次数、变压器变比情况比较

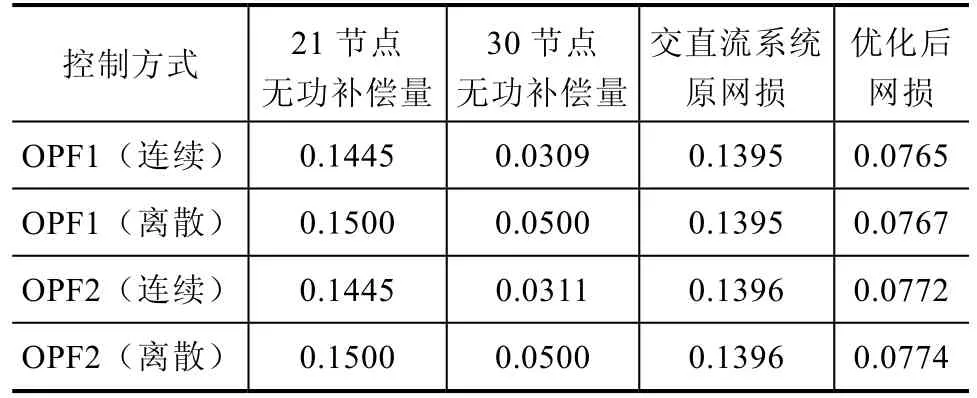
表5 各种控制方式下交直流系统的无功补偿及系统网损情况比较

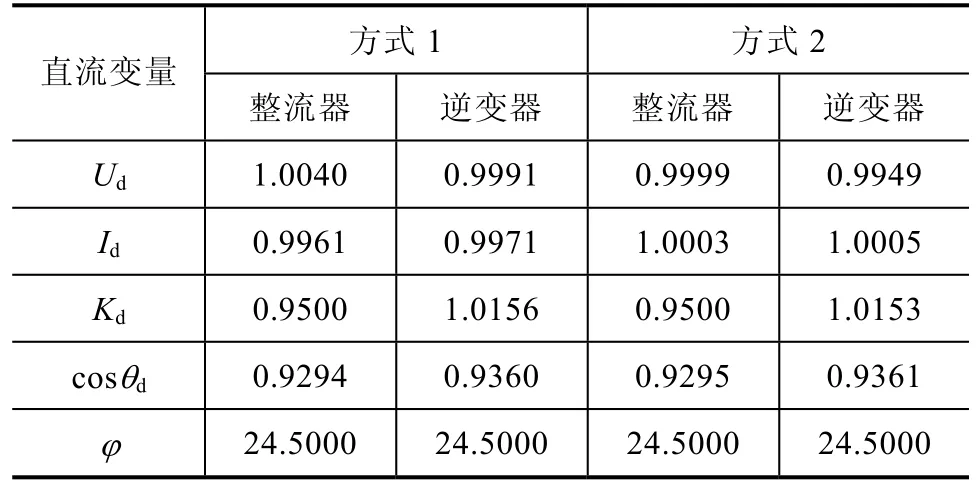
表6 IEEE-30节点无功优化计算下交直流系统变量

3.3 算例分析

5节点算例系统网络较小，在交直流系统的无功优化后网损小幅减少，5节点系统的无功补偿量和变压器的变比均在各分级节点上，优化效果较理想。

对表5的分析可知，30节点算例在优化后，网损有了明显的减小，这是由于节点电压值和相角值有了较好的改善，同时在考虑罚函数之后，计算网损比不含罚函数计算的网损稍大，这是由于考虑了变量的离散性，使其不能在理想的最优方式下运行的结果。

对表4、表5的分析可知，计算后的无功补偿量和变压器的变比均在各分级节点上，对含离散变量交直流系统的无功优化计算结果理想。

对图4、图5分析可知，收敛曲线在后面几次迭代变化缓慢，这是由于引入罚函数之后离散变量振荡造成的，但是依然可以可靠收敛。

4 结论

本文研究了一种计算交直流系统无功优化的方法，通过算例计算分析得到文章中方法的几个特点。

1）较强的离散变量处理能力。本文中的计算方法在内点法的基础上增加了对离散变量的处理，既利用了内点法的计算快速、寻优能力强的特点，又结合了罚函数的方法对离散变量进行优化，使得所用方法有较强的离散变量处理能力。

2）算法的适应性好、数值计算稳定合理。算法对两个算例进行计算，均能得到合理的计算结果，离散变量均在各个节点上，网损均有降低。同时通过离散处理方法和连续处理方法的对比可看出，采用离散处理方法，各离散变量虽无法达到理论上的最优解，网损与连续处理方法相比较大，但是结果更贴近实际。

[1] Asplund G, Eriksson K, Tollerz O. HVDC light-a tool for electric power transmission to distant loads[C]//VI Sepope Conference, Salvador, 1998.

[2] Weimers L. HVDC Light-a new technology for a better environment[C]//IEEE Winter Meeting, Florida, 1998.

[3] Weimers L. New markets need new technology[C]// 2000 International Conference on Power System Technology, VOLS I-III, Proceedings, 2000: 873-877.

[4] 张文亮, 汤涌, 曾南超. 多端高压直流输电技术及应用前景[J]. 电网技术, 2010, 34(9): 2-6.

[5] 李岩, 黎小林, 饶宏, 等. 高压直流输电技术自主化新发展[J]. 中国电力, 2009, 42(1): 41-44.

[6] 袁旭峰, 程时杰. 多端直流输电技术及其发展[J].继电器, 2006, 34(19): 61-67, 70.

[7] 欧阳昌裕. 实施西电东送战略促进东西部地区经济协调发展[J]. 中国电力, 2002, 35(10): 11-15.

[8] 陈潜, 张尧, 钟庆, 等. ±800kV特高压直流输电系统运行方式的仿真研究[J]. 继电器, 2007, 35(16): 27-32.

[9] 杨雄平, 罗向东, 李扬絮, 等. 南方电网直流闭锁故障时受端系统电压稳定问题分析[J]. 电力系统保护与控制, 2008, 36(22): 40-43.

[10] 余涛, 沈善德. 华中-华东多回HVDC辅助功率/频率控制[J]. 电力系统自动化, 2005, 39(1): 77-82.

[11] Lu C N, Chen S S, Ong C M. The incorporation of HVDC equations in optimal power flow methods using sequential quadratic programming techniques[J]. IEEE Trans on Power Systems, 1988, 3(3): 1005-1011.

[12] 刘云鹏, 曾文芳, 尤少华, 等. 在小电晕笼中分裂导线交流电晕的起始电压分析[J]. 高电压技术, 2011, 37(9): 2302-2306.

[13] 李国庆, 姚少伟, 陈厚合. 基于内点法的交直流混合系统可用输电能力计算[J]. 电力系统自动化, 2009, 33(3): 35-39.

[14] 邸弢, 李华强, 范锫. 基于奇异值分解和内点法的交直流系统无功优化[J]. 电工技术学报, 2009, 24(2): 158-163.

[15] 徐政. 交直流电力系统动态行为分析[M]. 北京：机械工业出版社, 2004.

[16] 赵晋泉, 侯志俭, 吴际舜. 牛顿最优潮流算法中离散控制量的新处理方法[J]. 电力系统自动化, 1999, 23(23): 37-40.

[17] 程莹, 刘明波. 求解离散无功优化的非线性原-对偶内点算法[J]. 电力系统自动化, 2001, 25(9): 23-27.

Research of Accurate Method for Solving Discrete OPRF Problem of AC-DC Transmission System

Zhang Xin Zhang Huiyun
(Jiaxing Power Supply Bureau, Jiaxing, Zhejiang 314000)

HVDC has been widely used in large-capacity power transmission recent years, which has outstanding advantages in terms of economics and operating characteristics, the use of AC-DC hybrid system among the regional power grid interconnection become an important way of transmission. OPF of AC-DC system especially OPRF problem is an important research direction, solving OPRF problem with discrete variables has been a difficulty. This paper combines principle of AC-DC system with reactive power optimization theory, devised a solution to the problem with discrete variable based on interior point algorithms. This paper uses minimum of network loss as objective function of OPRF problem and verifies the algorithm’s feasibility to solve the OPRF problem of AC-DC system with discrete variables through two examples.

AC-DC transmission system; interior point method; OPRF; discrete variable

张 昕（1987-），男，安徽省宣城市人，硕士，工程师，从事输配电线路研究工作。