基于电子雷达通信的追踪目标精度优化改进

欧仁侠， 张华磊， 陈洪斌， 邓 芳

(1.吉林医药学院,生物医学工程学院,吉林 吉林 132013; 2.中国人民解放军93057部队，吉林 吉林 132102; 3.湖北第二师范学院 计算机学院，武汉 430025)

基于电子雷达通信的追踪目标精度优化改进

欧仁侠1， 张华磊2， 陈洪斌1， 邓 芳3

(1.吉林医药学院,生物医学工程学院,吉林 吉林 132013; 2.中国人民解放军93057部队，吉林 吉林 132102; 3.湖北第二师范学院 计算机学院，武汉 430025)

在无需传感器系统中实现了工作性能良好、精准时间的航迹关联雷达通信，采用Bar Shalom-Campo航迹融合算法优化设计了无反馈形式的分布式航迹融合。理论分析表明，算法能够通过先验信息，实现运算量以及运算难度的降低。实验结果得到：改进的算法的雷达通信过程中误差明显小于单个传感器的误差；优化的航迹融合算法与单一雷达的滤波相比能够显著提高定位精度，定位性能有了明显的改进；优化算法后的系统能够达到多传感融合改进目标定位。这一研究对最大程度的优化系统的工作能力具有明显的理论和实践应用价值。

雷达通信； 追踪目标； 滤波； 传感器

0 引 言

随着当前计算机雷达通信的飞速发展，目标定位的研究已经集成了电子、通信、信息技术等多学科融合。在一个区域内的多台传感器通过网络的形式，将其数据进行联网共享，这种信息融合技术是当今世界各国很多科研者竞相研究的热门课题[1]。最先研究该技术并且进行应用的国家是美国，在这个领域上一直占据着领头羊的位置。此外，英国也出现了较为领先的成果，如DFF信息融合技术。虽然我国也开始在该领域着手研究。经过一定时间的积累，但是和世界其他国家相比，我国在这方面的研究还有很长一段路要走[2-3]，还需继续在理论以及实际应用方面做更加深层次的研究，进而达到世界领先水平。多个传感器在分布式形式下，整个系统需要进行信息融合中的最核心的部分是航迹关联，该部分具有较大的实际价值。有关学者对航迹关联课题的理论做了很多的研究和分析工作[4]。Singer团队率先提出了加权航迹的概念，而最近领域法则是由Kosaka课题组率先提出的，而空间与时间进行结合的方式则率先由中科院课题组提出[5-6]。如果将系统采用不同框架划分，常将航迹关联分成集中式和分布式2种。在集中式的航迹关联中，因为传感器以及其到融合系统枢纽中心的通信宽带会有制约，同时要求融合中心的传感器系统具有较强的工作性能，所以这种方式实用性不强。然而，分布式方法一般是先把某些传感器处理好一部分计算以及信息数据，再把数据进行压缩传送到中心，这样该方式的实用性较强。由此可见，分布式方式的航迹关联是人们常常采用的方式[7-9]。在分布式的雷达系统里，航迹关联在系统中处于很重要的位置，有着较为明显的实用价值。本文基于这一背景，进行了分布式航迹融合算法的改进设计及实验分析，这一研究对最大程度的优化系统具有明显的理论和应用价值。

1 算法优化的设计

在分布式系统中，任意一个传感器都先自身做数据处理，然后把部分航迹传输到中心作处理。

1.1 融合算法设计

1.1.1 凸组合的航迹融合

(1)

经过融合以后的误差协方差为

(2)

这样可以将其推广，得

(3)

(4)

1.1.2 Bar Shalom融合算法

Bar Shalom课题组提出以下的航迹状态的估计：

(5)

则Dij的协方差阵为

(6)

式中，Pij、Pji，通过K滤波估计，则有：

(7)

进而得

(8)

这就是Bar Shalom的航迹融合算法，他对简单凸组合有了一定的考虑，本算法也结合考虑了这一模型。

1.2 无反馈的最优算法设计

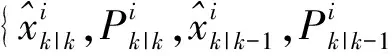
若存在N个传感器都在追踪一个目标，且存在一个k时刻，则该时刻的目标运动以及量测方程能有如下表述：

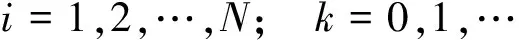
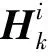
(11)

进而，可以推导

(12)

式中,vk满足

(13)

在预测通报以及更新上能够递推运算得到协方差阵的逆阵，即是信息卡尔曼滤波器。通过上述模型类推，可以得到k时刻方程为

(14)

式(14)两边相乘，得

(15)

依照上式有

(16)

这样，得到优化算法状态估计方程和全局估计误差协方差分别为：

(18)

分析上述模型过程可以发现该算法通过先验信息，不需要求出差协方差，这样就很大程度上降低了运算量以及运算难度。另外，此算法基于量测扩维，采用矩阵变化得到的，将其应用在全局是最佳选择。

2 实验分析

图1给出了实验模型的传感器观测航迹的位置信息。

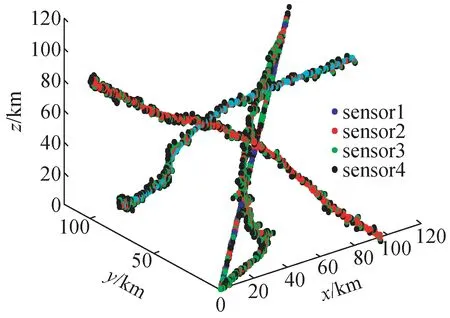
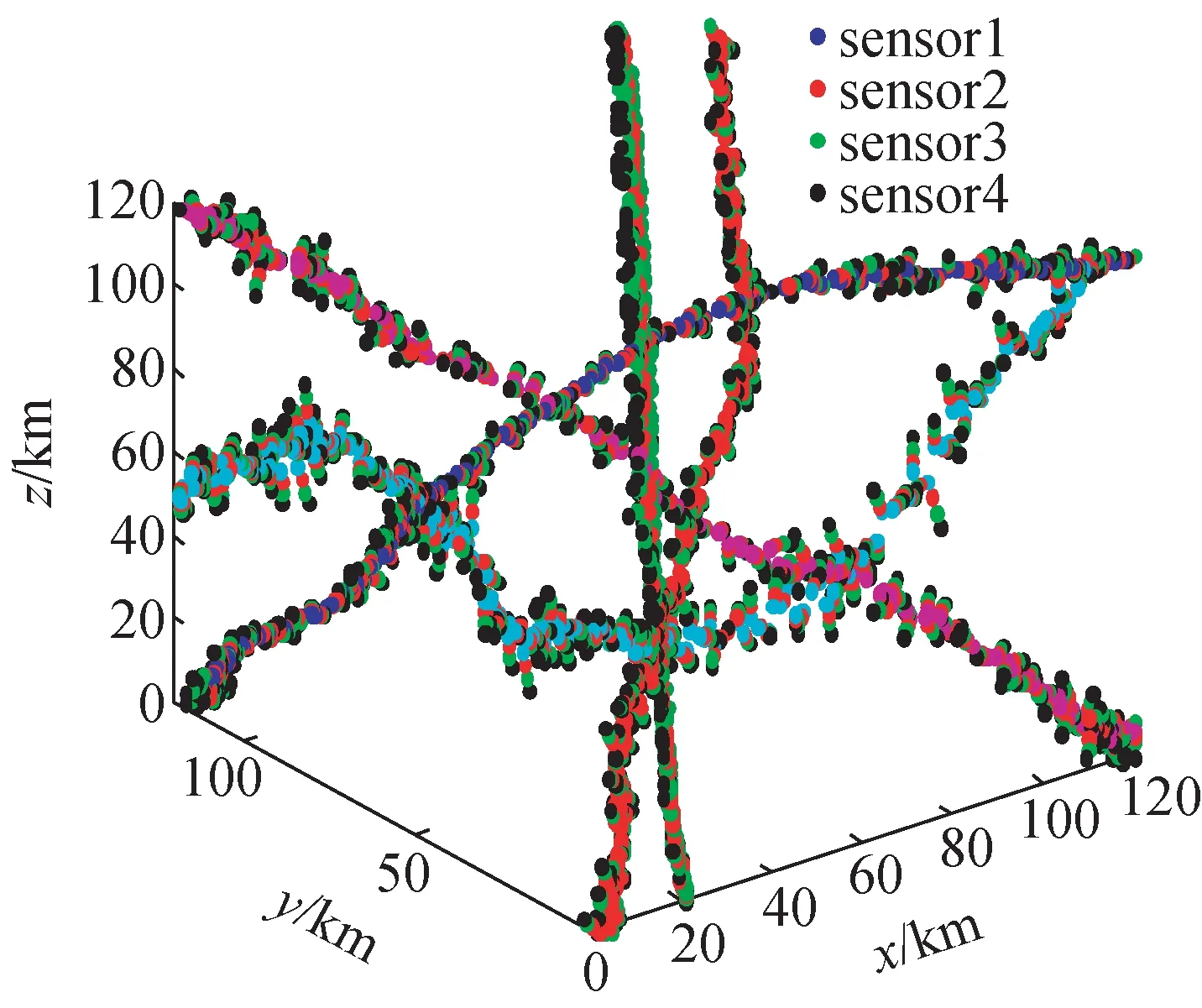
图1 实验模型的传感器观测航迹

2.1 匀速飞行的航路的实验

首先，对匀速飞行的航路进行分析， 实验环境如下：在1 km高空，分别采用20、100 m/s，时间为50 s，图2所示为匀速仿真对比数据结果。

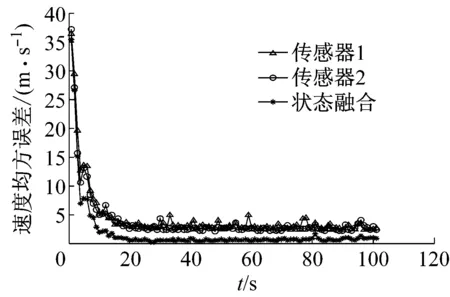
图2 匀速条件下算法的后速度均方误差对比

2.2 匀加速飞行的航路的实验

目标在距离参考原点长3 km、宽4 km、高1 km处的方位开始飞行，并且用20、100 m/s，跟踪为50 s，在X轴以-10 m/s的加速度变化，图3～5所示为匀加速仿真对比数据结果。

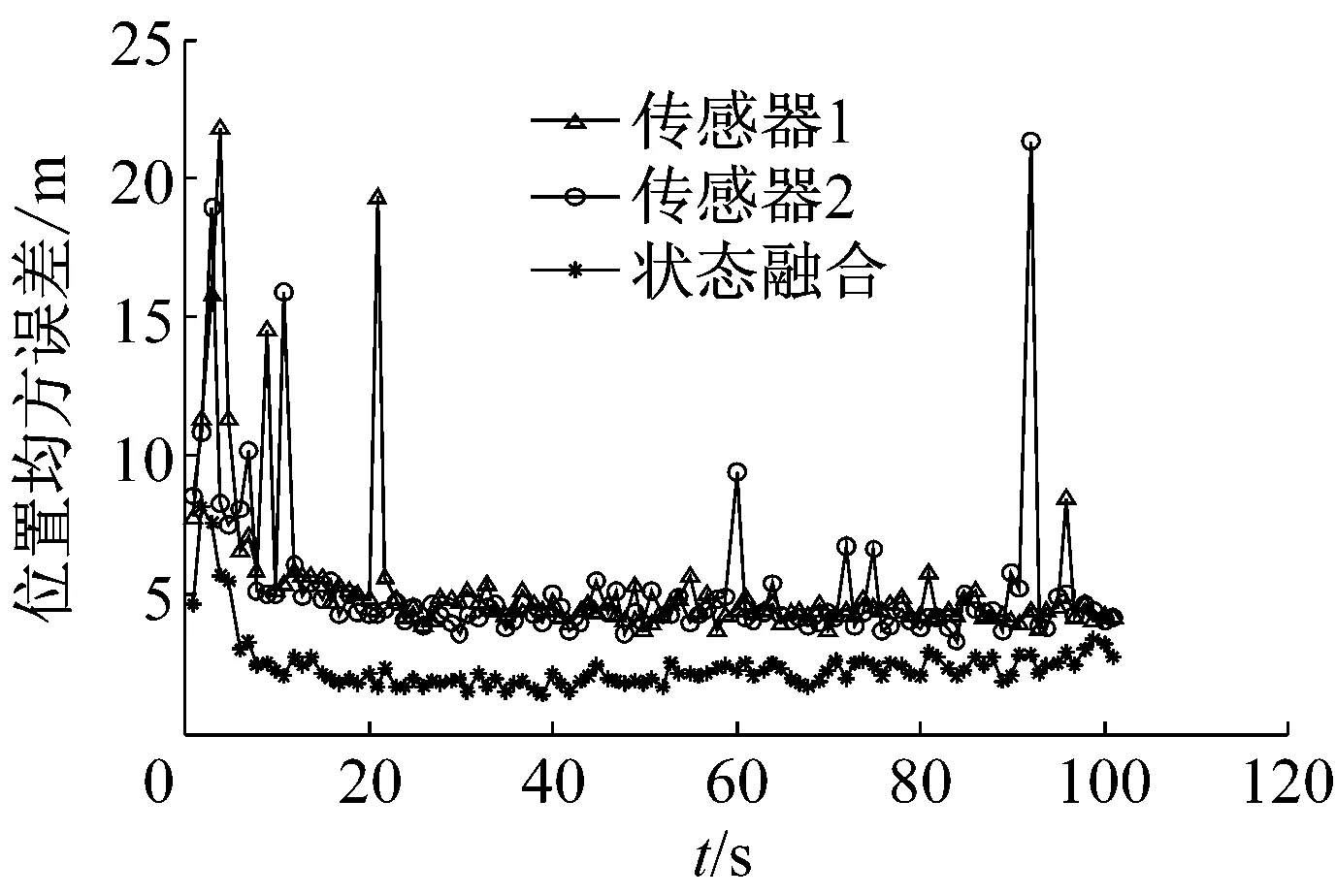
图3 匀速条件下算法的后位置均方误差对比

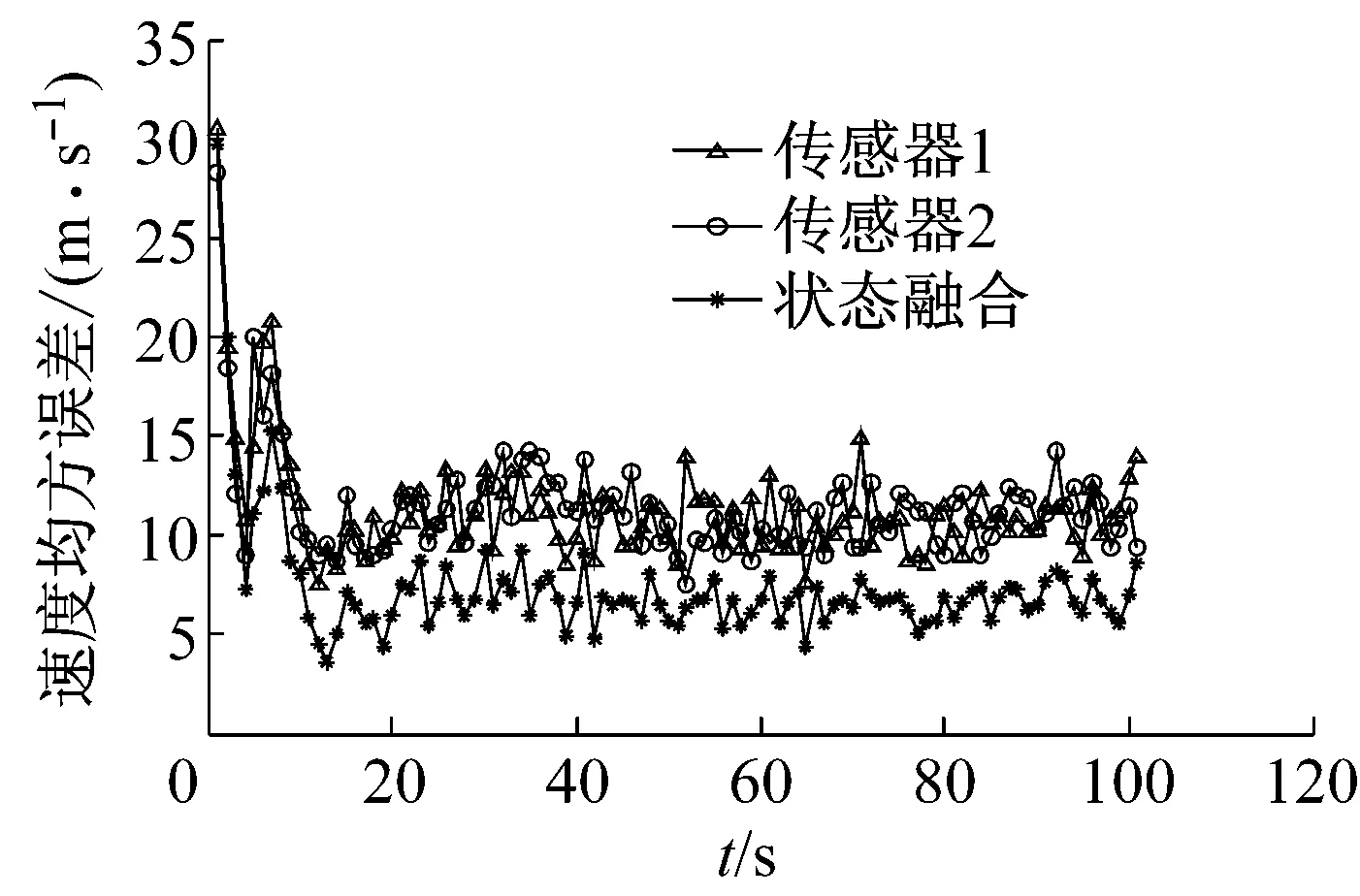
图4 匀加速条件下算法的后速度均方误差对比

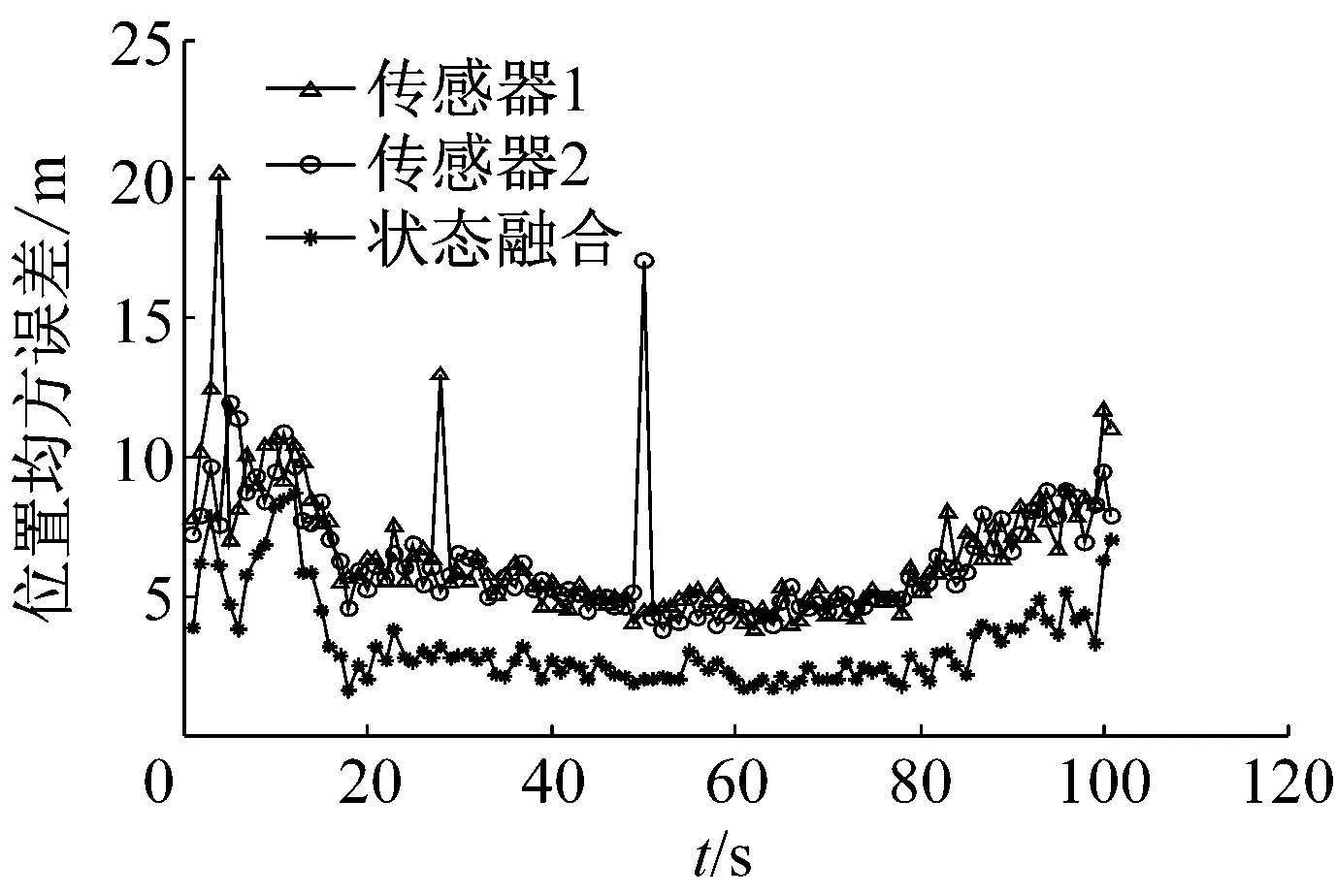
图5 匀加速条件下算法的后位置均方误差对比

2.3 上仰机动飞行实验

目标在距离参考原点长3 km，宽4 km，高1 km处的方位开始飞行，并且在开始的1～15 s的时间段按20、100 m/s，在15～34 s按0.17 rad/s发射转动，接下来-20、100 m/s匀速，图6、7所示为上仰机动飞行的仿真对比数据结果。

图6 上仰机动条件下算法的后速度均方误差对比

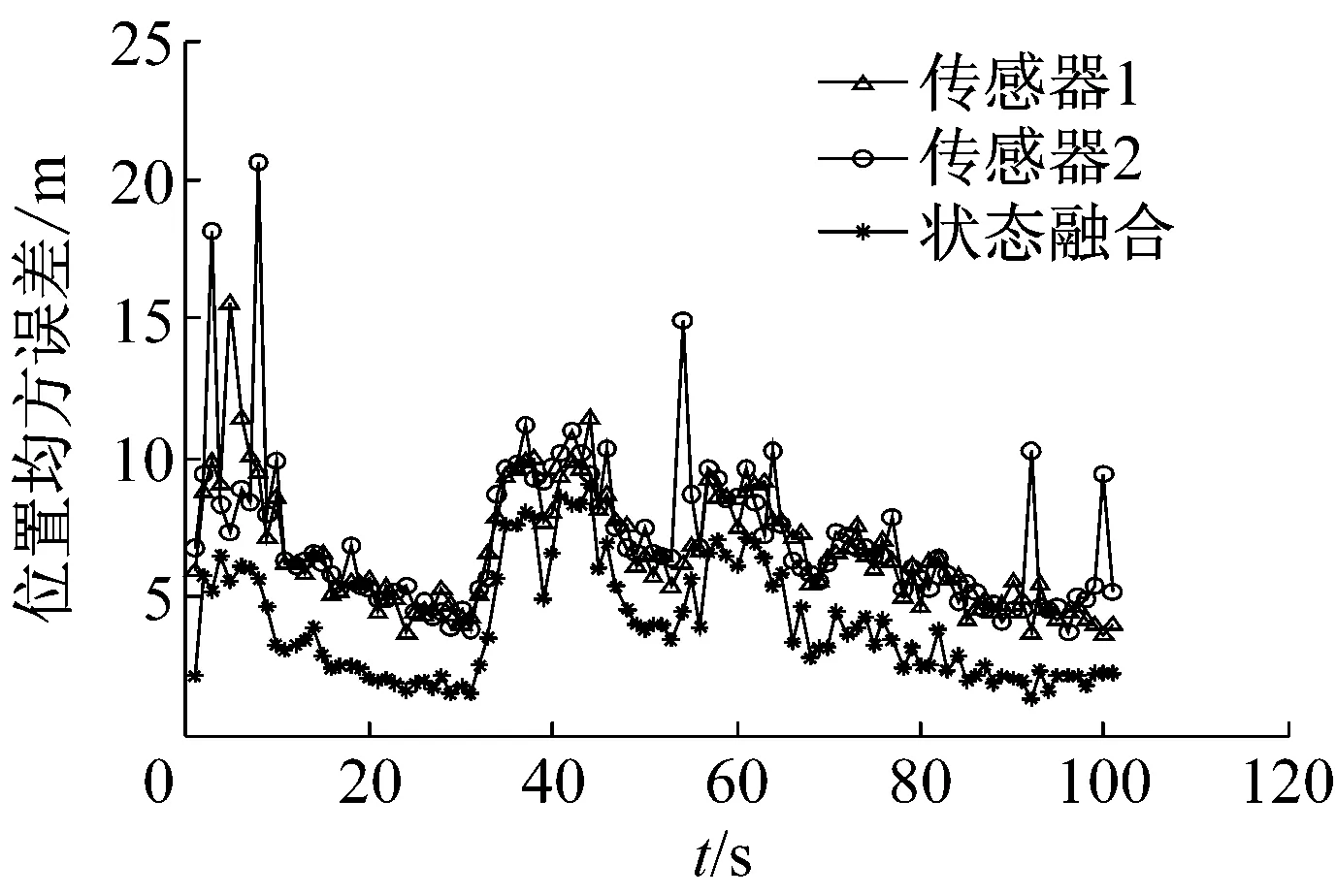
图7 上仰机动条件下算法的后位置均方误差对比

实验结果分析：在上述3种目标飞行的的测量误差范围内，本文进行50次的蒙特卡洛仿真实验。由仿真实验最终的结果明显的能够观察到，在基于无反馈最佳方式的分布式背景下，航迹融合算法比单个雷达I mm滤波很明显在追踪目标的精度上得到了提升，并且优化了系统的运行性能。另外，不管是在机动还是没有机动的飞行航路里，都可以满足预想的需求，还验证了多个传感器融合系统能够提高追踪目标的精度，在实际应用中，起到了很好的支撑作用。

3 结 语

如果航迹自身距离比较大，又没有干扰发生的时，对航迹关联就较为容易操作。一旦出现航迹比较多，目标也多，同时又有多种干扰如噪声、杂波等的情况下，要对航迹进行关联，就比较困难。另外，各传感器又回存在距离、位置等因素的综合不均衡，一些误差如方位、目标位置误差、坐标转换误差等其他情况造成的影响，关联问题的难度会更加复杂。为解决关联存在的问题，本文通过利用分布式融合算法，对在无反馈的背景下，对几条航路做了融合处理，经过50次的蒙特卡洛仿真实验结果，可以验证该算法成功实现了预想中的融合精度要求。随着科技的发展，系统处理器工作的能力一定会更强，在实际应用时，可以结合精度要求，选取更加合理精确的算法方案，可最大程度上优化系统的工作能力。

[1] Medley B, Joughin I, Das S B,etal. Airborne-radar and ice-core observations of annual snow accumulation over thwaites glacier, west antarctica confirm the spatiotemporal variability of global and regional atmospheric models[J]. Geophysical Research Letters, 2013, 40(14):3649-3654.

[2] Li Y. Recent Antarctic ice mass loss from radar interferometry and regional climate modelling[J]. Nature Geoscience, 2008, 1(2):106-110.

[3] Farr T G, Rosen P A, Caro E,etal. The shuttle radar topography mission[J]. Reviews of Geophysics, 2000, 45(2):37-55.

[4] 李晓柏,杨瑞娟,陈新永,等. 基于分数阶傅里叶变换的雷达通信一体化信号共享研究[J]. 信号处理,2012,10(4):487-494.

[5] Massonnet D, Briole P, Arnaud A. Deflation of Mount Etna monitored by spaceborne radar interferometry[J]. Nature, 1995, 375(6532):567-570.

[6] 李晓柏,杨瑞娟,程伟. 多相伪随机序列在雷达通信一体化中的应用[J]. 信号处理,2012,10(11):1543-1550.

[7] Goldstein R M, Zebker H A, Werner C L. Satellite radar interferometry-Two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4):713-720.

[8] 胡玉平. 基于舰载相控阵雷达的一体化通信系统研究[J]. 现代雷达,2008,12(1):22-25.

[9] 刘少华,黄志星. 基于扩频的雷达-通信一体化信号的设计[J]. 雷达科学与技术,2014, 12(1):69-75.

Improvement of Accuracy of Electronic Radar Communication in Tracking Target

OURenxia1,ZHANGHualei2,CHENHongbin1,DENGFang3

(1. School of Biomedical Engineering, Jinlin Medical College, Jilin 132013, Jilin, China; 2. The 93057 Troops of Chinese People’s Liberation Army, Jilin 132102, Jilin, China; 3. College of Computer, Hubei University of Education, Wuhan 430025, China)

In this paper, we implement a system which has no sensor, and shows good work performance in radar communication. The Bar Shalom-Campo track fusion algorithm is applied to optimize the design of distributed track melting, and is without feedback. Theory analysis shows that the algorithm can reduce the computational cost and the operation difficulty by a priori information. The experimental results indicate that the error of improved algorithm is much smaller than a single sensor in the process of radar communication. Furthermore, compared with single radar IMM filtering the optimization of track fusion algorithm can significantly improve the positioning accuracy. The optimization algorithm used in the system can achieve multiple sensor fusion target improvement. This study has significant theoretical and practical value to the optimization of system work ability.

radar communication; track targets; filtering; sensors

2016-04-05

国家自然科学基金项目(514061)

欧仁侠(1980-)，女，吉林农安人，硕士，讲师，主要从事电子、通信及信息处理研究。

Tel.:15044216395;E-mail:15044216395@qq.com

1006-7167(2017)02-0117-04