有入渗时地下水位变动下的分水岭移动规律

胡 强， 肖先煊， 袁文杰， 蔡国军， 梅 杰

(成都理工大学 环境与土木工程学院； 国家级地质工程实验教学示范中心, 成都 610059)

·仪器设备研制与开发·

有入渗时地下水位变动下的分水岭移动规律

胡 强， 肖先煊， 袁文杰， 蔡国军， 梅 杰

(成都理工大学 环境与土木工程学院； 国家级地质工程实验教学示范中心, 成都 610059)

根据相似原理，在室内建立能模拟地下水分水岭移动特征的模型。模拟一定降雨条件下，保持一侧河渠水位不变，改变另一侧水位，并加入示踪剂，观察不同水位差时地下水运动特征并记录测压管水位，绘制潜水位与分水岭形态，实测分水岭位置，得到试验数据，并对比不同水位差下地下水分水岭的移动特点。同时，根据已知的模型参数，由河间地块潜水流浸润曲线方程与分水岭位置计算式得到理论潜水位和分水岭位置，并与实测值相比。结果表明：通过公式计算得到的理论潜水位和分水岭位置与实际试验测得的数据相吻合，但存在临界值Cr，当两侧水位差Δh>Cr时不再适用，临界值大小与流体密度、动力黏性系数、渗流断面平均流速、砂样平均粒径等有关。

潜水; 入渗补给; 河间地块; 水位差; 分水岭移动

0 引 言

近年来，我国水资源形势日趋紧张，政府批准了一系列引水调水工程缓解城市水资源匮乏的现状，如滇中引水工程[1]、南水北调工程。我国一些粮食主产区,如河南、山东近年来多次遭遇干旱天气，农业部门积极兴修水利以消除旱情对农业生产的影响。水库选址也要充分考虑蓄水后侧向渗漏问题。在一系列水利工程建设中有很大可能出现地下水分水岭移动引起水文地质灾害或环境问题[2-4]。研究地下水潜水位及分水岭的移动规律，进而通过人工控制水位[5]，防止水库发生侧向泄漏[6-8]和河间地块盐渍化[9-11]或沼泽化[11]。城市垃圾填埋场或核废料埋置点选址，也要充分研究地下水分水岭运动规律防止发生泄漏造成污染[12]。因此，研究有入渗补给时地下水水位及分水岭移动规律具有一定意义。

前人对河间地块潜水位与分水岭位置的研究多是通过理论推导而来，通过相应理论公式计算得到的潜水位和分水岭位置与实际情况是否相近需要实践证明。本文试图在前人研究的基础上，在实验室建立河间地块砂槽模型，一定入渗条件下，改变两侧河渠水位高度，通过测压管和示踪剂，测得河间地块潜水位和分水岭位置，比较实测潜水位和分水岭位置与公式理论计算值，验证公式实用性，为实际生产中确定分水岭位置和控制潜水位提供理论依据。

1 试验模型

薛禹群等[11]提出了潜水流浸润曲线方程和河渠间有入渗时，河渠间分水岭位置计算式:

(1)

(2)

式中：x为距左端起始断面的距离；h为河间地块距左端起始断面x处的潜水流厚度；h1为左侧河渠边河流高度；h2为右侧河渠边河流高度；L为两河渠之间的距离；K为河间地块含水层的渗透系数；W为入渗强度；a为分水岭位置。

上述公式推导条件为：① 含水层均质各向同性，底部相对隔水层水平，上部有均匀入渗，可用入渗强度W表示；② 河渠间彼此平行，应用裘布依假设，通过垂向平均，潜水流可视为一维流，符合达西定律；③ 潜水流是渐变流并趋于稳定[11]。此外两侧河流为定水头边界。因为在河间地块研究剖面内河渠的水位是由剖面以上大面积的、多种形式的水量补给所决定的,而受局部范围潜水排泄补给的影响很小，所以，这种假定是允许的[13]。

以均质各向同性河间地块为模拟对象，建立砂槽模型(见图1)。建模过程中，遵循几何相似原则，即① 几何相似；② 运动相似；③ 动力相似；④ 边界条件相似[14-15]。

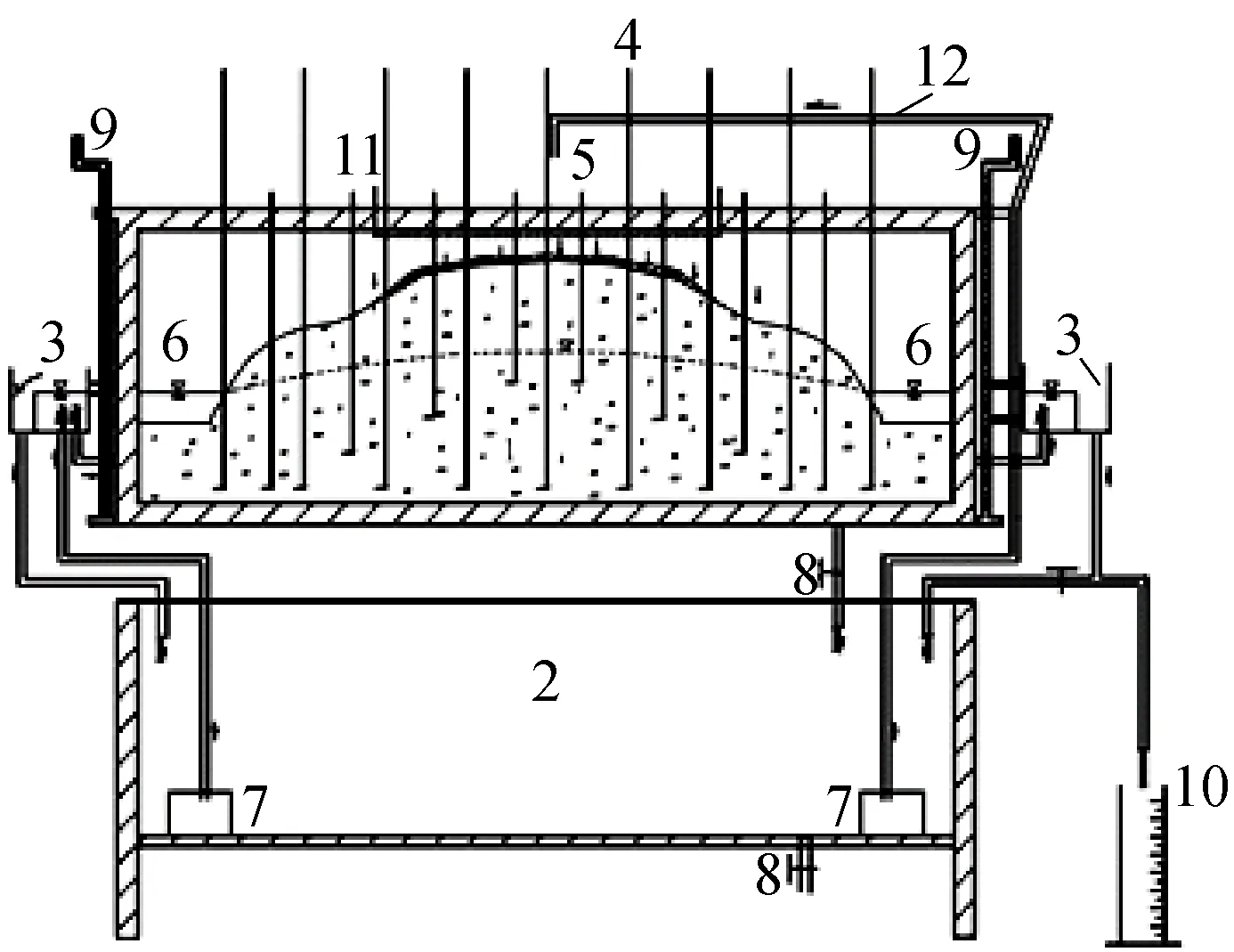
图1 河间地块潜水砂槽模型

河间地块潜水模拟箱(长×宽×高)1.9 m×0.4 m×0.8 m。单侧设置9排测压管，每排1支，管径φ=10 mm,L=1 m，测压管距左侧河流的距离分别为0，20,40.7, 61, 75.7, 90.5, 111, 131 ,148 cm。同侧有8支25 mL的示踪剂注入管, 为增大试验测量分水岭位置的精确度，在模拟箱顶部增加5支示踪剂注入管。蓄水箱容量(长×宽×高)=1.8 m×0.5 m×0.35 m。模拟箱顶部安装雨筛，使给水能模拟区域降雨，实验中要确保模拟降雨全部入渗，不能形成地表径流。为控制左、右侧河渠水位，在渗流试验箱体的左、右端附有可通过升降系统控制高程的排水溢流箱[14]。模拟箱内接受降雨入渗的区域面积为2 910.48 cm2。试验填充为均质石英砂，粒径0.1～1.0 mm，通过筛分实验得到粒径级配曲线(见图2)。得到d50=0.6 mm,Cu(不均匀系数)=5.14，Cc(曲率系数)=2.1。装置所用石英砂为级配良好的不均匀土[16]。

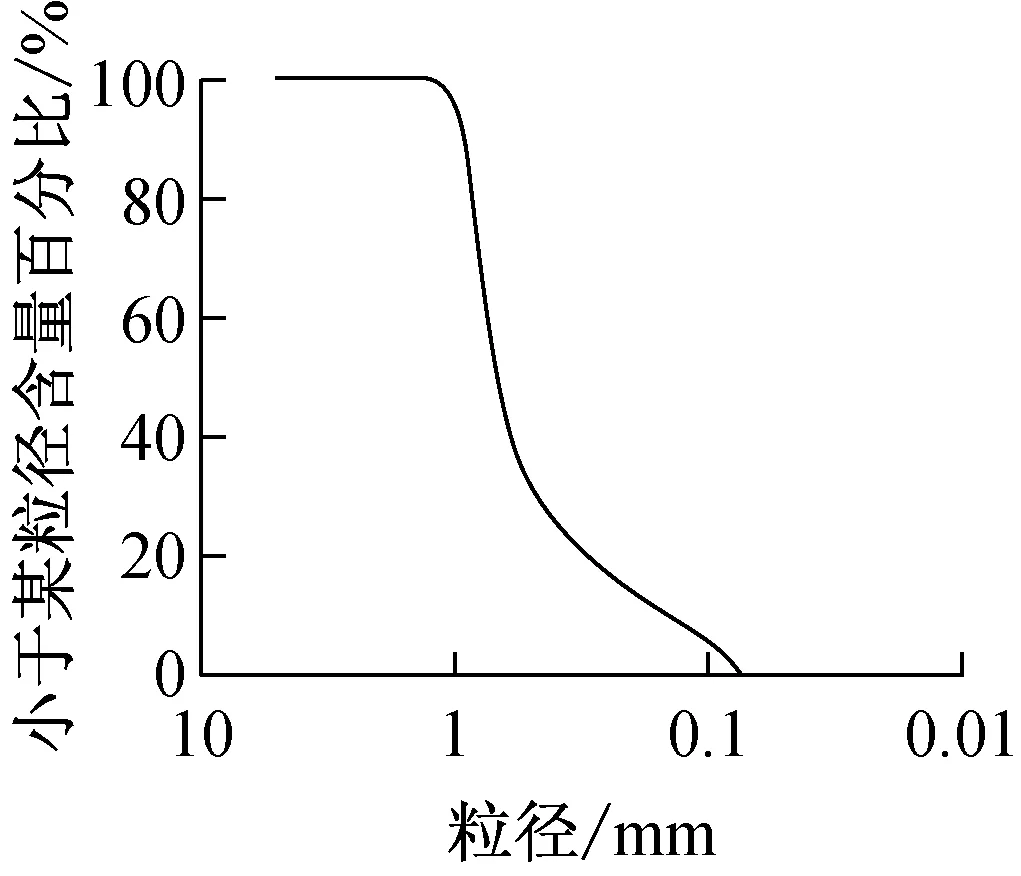
图2 粒径级配曲线

表1 渗流试验数据

图3 毛细水上升高度随时间变化曲线

2 结果处理

河间地块为石英砂填充，试验中不予变化，因此在本次试验中K值不变，K=0.238 cm/s。打开抽水泵，在模拟箱顶部形成降雨，试验中保证降雨全部均匀入渗，不形成地表径流。通过升降装置调节两侧水位高度h1、h2,实验中h2水头保持不变。待溢流箱流出的水量稳定后，测量一定时间t内左、右两侧溢流箱水量V1、V2，采用水量时间法计算装置流量Q=(V1+V2)/t，得到入渗强度W=Q/S，S为入渗区面积。加入示踪剂，观测示踪剂运动特征和分水岭位置，测量分水岭到左侧河渠距离a1，观察测压管记录潜水水位，将试验参数代入式(1)、(2)，得到理论潜水位与理论分水岭位置a2，用计算机绘制潜水位。重复试验3次，观测分水岭位中间、偏移、消失的现象。将实际测量结果与式(1)、(2)理论计算结果比较，验证其实用性。3次试验数据记录见表2。从表2可知，3次试验计算得到W分别为0.033、0.034、0.034 cm/s，可以认为试验中入渗强度W保持不变。通过实测和公式计算分别得到实测分水岭a1与理论分水岭位置a2，见表2。

2.1 两侧水位相等

调节溢流箱高度，h1=37.7 cm、h2=37.6 cm,因读数误差和仪器精度，可以认为河流水头相等。试验现象见图4。由图5可见，实测水位h与理论水位H存在差值,但均不超过5%，可以认为结果一致。分析误差由读数误差和测压管水头损失以及仪器精度等造成。试验表明，当两侧水位相等时，通过式(1)、(2)计算分水岭位置、潜水位高度与实际相吻合。

表2 3次试验数据记录

图4 两侧河水位相等时地下水运动轨迹图

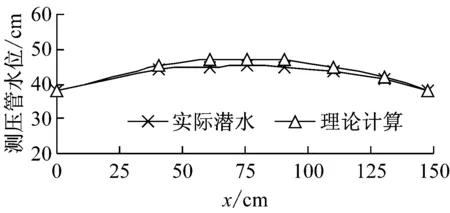
图5 两侧水位相等时地下水位曲线

2.2 两侧有水位差且分水岭存在

待第1次试验所加入示踪剂完全消失后，升高左侧溢流箱高度，待流量稳定后，测得h1= 48.8 cm、h2=38 cm,由于试验装置排水孔较小，h2由37.6 cm升高至38 cm。试验现象见图6，可以观测到，分水岭向水位较高的左侧发生偏移。

图6 两侧有水位差且分水岭存在地下水运动轨迹

由图7可知，实测水位h与理论水位H相对误差不超过5%，考虑到仪器精度、读数误差以及测压管水头损失，可以认为理论结果与实测数据一致。实测分水岭位置a1=53.80 cm,通过式(2)计算得到理论分水岭。位置a2=51.56 cm，两者相差为2.24 cm, 因仪器精度和读数误差，可以认为a1=a2。试验表明，当两侧河渠有水位差且分水岭存在时，通过式(1)、(2)计算分水岭位置、潜水位高度与实际相吻合。

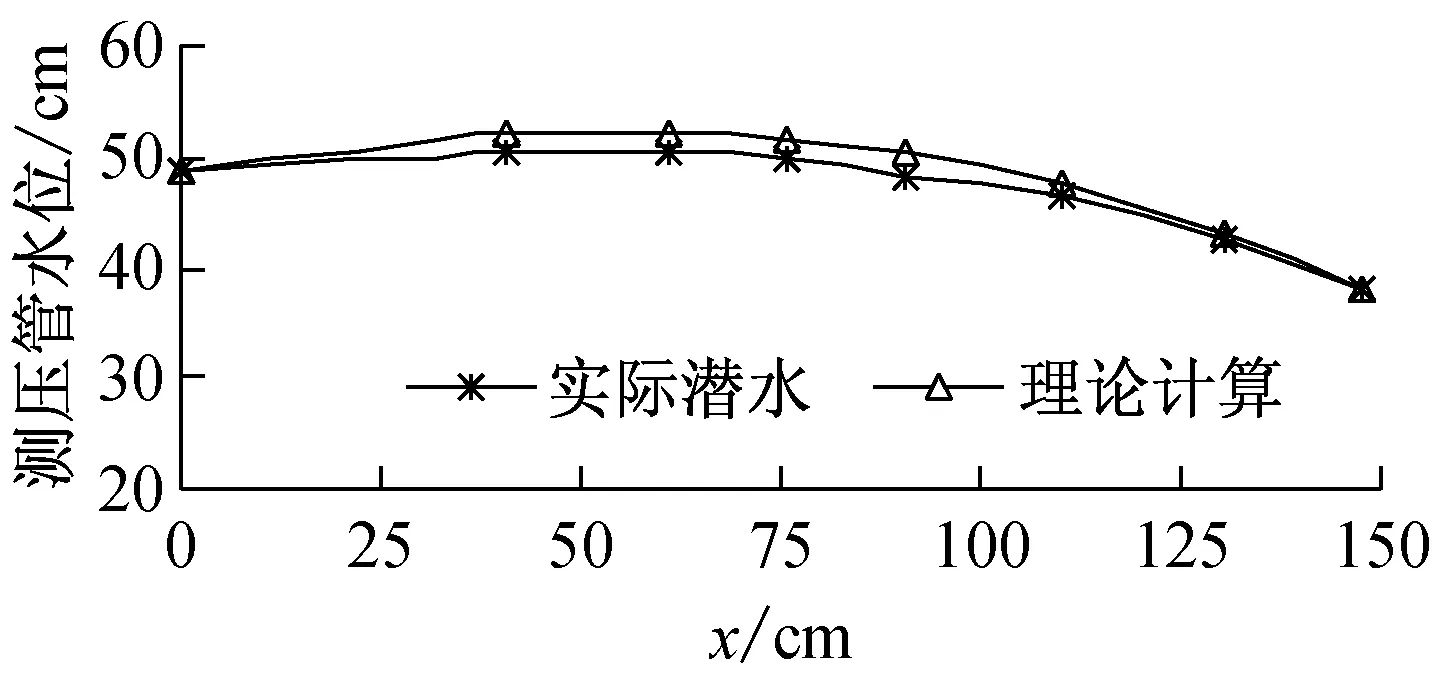
图7 两侧有水位差且分水岭存在地下水位曲线

2.3 两侧有水位差且分水岭消失

待示踪剂完全消失后，继续升高左侧溢流箱高度，待流量稳定后，测得h1= 54.7 cm、h2=38 cm，试验现象见图8。由图9可知，实测结果与理论计算结果差别较大。随着两侧水位差Δh继续增大，潜水流浸润曲线方程和河渠间分水岭位置计算式与实际结果相差较大，不再适用。

图8 两侧有水位差且分水岭消失地下水运动轨迹

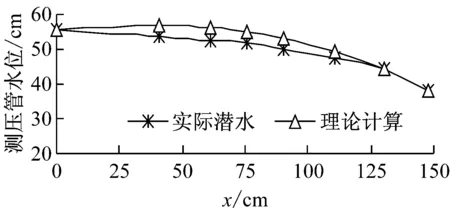
图9 两侧有水位差且分水岭消失地下水位曲线

2.4 临界水位差Cr

由3次试验可知，两侧河渠水位差Δh增大，分水岭向水位较高一侧偏移。同时，随着Δh增大，地下水流速v增大，在试验2.3中出现公式便不再适用，由达西定律计算得到试验2.3中的流速v=270 μm/s与通过水量时间法计算地下水流速v=500 μm/s相差较大。根据雷诺数Re计算式[19]，计算试验2.3中Re，其中ρ=1 g/cm3，v=500 μm/s，d=0.6 mm，10℃下水的黏性系数[19]μ=1.308 Pa/s。计算得到Re=22.9>10。因此，随着Δh的增大,试验条件下Re超过达西定律适用范围雷诺数1Cr时，式(1)、(2)不再适用。在试验条件下，计算得到Re=10时，地下水流速v=190 μm/s，根据达西定律得到Δh=VL/K=13.55 cm，即Cr=13.56 cm。

从表6可知，试验3.1、试验3.2中ΔhCr时，不能在实际中利用潜水浸润曲线方程和分水岭计算公式来确定分水岭位置与潜水位。

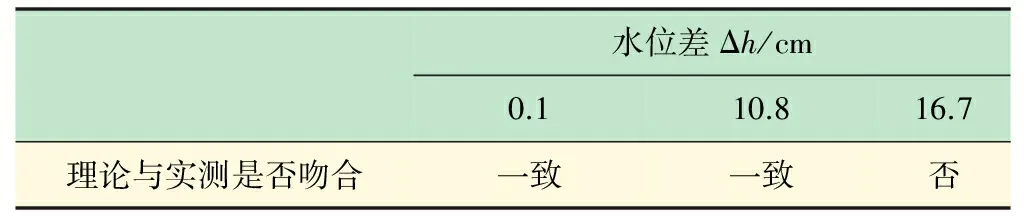
表6 水位差Δh与理论计算吻合度

3 结 论

通过本研究，可获得以下结论与认识：

(1) 在模型试验中，河间地块水位受到两侧河渠水位高度影响，在均质各向同性、底部隔水层水平河间地块中，入渗强度不变，地下水运动满足一维稳定流条件下，通过式(1)计算得到潜水水位与实际潜水位吻合，因此，可用式(1)来计算潜水位。

(2) 在均质各向同性、底部隔水层水平的河间地块中，入渗强度不变，地下水运动满足一维稳定流条件下，分水岭位置受到两侧水位高度的影响，偏向水位较高一侧。在已知渗透系数、入渗强度时即可通过式(2)来确定分水岭位置。

(3) 一定入渗强度下，两侧水位差影响公式的实用范围。存在一个临界值,当水位差大于临界值时，不再利用潜水浸润曲线方程和分水岭计算式来确定潜水位和分水岭位置。临界值受流体密度ρ和动力黏性系数μ、渗流断面平均流速v、砂样的平均粒径d影响，由式Cr=ReμL/(Kdρ)确定，其中Re=10。

本研究可为均质各向同性河间地块中两侧河渠间距确定、河间地块潜水位控制等问题提供理论依据。

[1] 瞿霜菊，黄 辉，曹正浩. 云南省滇中引水工程规划研究[J].人民长江，2013,44(10)：80-83.

[2] 焦致娴. 滇中引水工程对水源区及水源工程下游段陆生生态评价区植被影响初步研究[D].武汉：华中师范大学,2012.

[3] 冯 健，周怀东，彭文启,等.滇中引水工程对洱海水环境影响[J].中国水利水电科学研究院学报，2012, 10(4):241-246.

[4] 廖晓超，许 模，蒋 莉.中坝隧道地下分水岭演化的数值模拟分析[J].地下水，2014(1):48-49.

[5] 陈文芳.中国典型地区地下水位控制管理研究[D].北京：中国地质大学(北京),2010.

[6] 夏金梧，吴玉华，罗小杰,等.江坪河水利枢纽库首右岸河间地块岩溶渗漏分析[J].人民长江, 1994(8):41-45.

[7] 周志芳，李 艳.清江隔河岩水利工程河间地块渗漏估算[J].河海大学学报, 1996(5):101-104.

[8] 陈运东.重庆市藻渡水库左岸河间地块渗漏评价[J].工程地质学报，2014(22)：244-248.

[9] 张 红，章光新，杨建锋,等.人工控制潜水位下苏打盐渍土水盐动态分析[J].干旱区资源与环境,2008,22(5):149-154.

[10] 赵海卿.吉林西部平原区地下水生态水位及水量调控研究[D].北京：中国地质大学(北京),2012.

[11] 薛禹群，吴吉春.地下水动力学[M].3版.北京：地质出版社，2011：53-56.

[12] 郑 佳.北京西郊垃圾填埋场对地下水污染的预测与控制研究[D].北京：中国地质大学(北京),2009.

[13] 张明泉.河间地块潜水分水岭移动规律的初步探讨[J].兰州大学学报,1986(4):112-117.

[14] 肖先煊，许 模，蔡国军,等.抽水试验模型与地下水动力学实验教学试验[J].实验室研究与探索，2014,33(1):164-168.

[15] 虞修竞，蔡国军，付小敏,等.水文地质实验装置的研制及应用[J]. 实验室研究与探索，2011,30(3)：209-212.

[16] 陈仲颐，周景星，王洪瑾.土力学[M].北京：清华大学出版社,1994：3-7.

[17] 虞修竞，付小敏，苏道刚.水文地质学实验教程[M].成都：西南交通大学出版社,2008：30-34.

[18] 张人权，梁 杏，靳孟贵,等.水文地质学基础[M].6版.北京：地质出版社,2011：20.

[19] 柯 葵，朱立明.流体力学与流体机械[M].上海：同济大学出版社,2009：237.

The Test of Watershed Movement Regulation Induced by Water Table Fluctuation When Infiltrated

HUQiang,XIAOXianxuan,YUANWenjie,CAIGuojun,MEIJie

(Collage of Environment and Civil Engineering; Laboratorial Center for Geo-engineering,Chengdu University of Technology, Chengdu 610059, China)

On the condition of constant infiltration strength, how to acquire the level of groundwater and the watershed position between two parallel ditches are worth studying. Previous scholars issued the theoretical formulas of water table curve and watershed position between two parallel ditches. However, the practice of formulas still need verifying. As a result, we built a model which could imitate the watershed movement indoor according to the similar principle. On the precondition of stable recharge, we kept one side water level constant and changed the other side level. By observing the path of groundwater after adding to tracer, we noted the level of piezometer tube, drew the form of watershed, and compared the watershed characteristic in the different water level. Meanwhile, we obtained a group of academic data by the formulas of water table curve and watershed position and compared with test data. The result showed we could acquire the level of groundwater and the watershed position by formulas. But there is a critical value if water level difference beyond a threshold the formulas will not work. The critical value is related to fluid density, dynamic viscosity coefficient, average flow velocity and average particle size.

phreatic water; infiltrated recharge; parallel ditch; water level difference; watershed moving

2016-05-16

国家自然科学青年基金项目(41202209)；成都理工大学中青年骨干教师培养计划(HG0092)；省级专业综合改革与实践教学项目(SZH1103ZX08、16Z0547)

胡 强(1995-)，男，山西交城人，本科生，地下水科学与工程专业。

Tel.:18428381167； E-mail.：2540746843@qq.com

肖先煊(1985-)，男，江西吉安人，讲师，主要从事地下水实验教学工作。

Tel.:028-84077667； E-mail.：sassoon1123@126.com

P 641.2

A

1006-7167(2017)02-0014-04