基于FPGA和STM32的脉宽频率测量方法

潘 宇

(白城师范学院 物理学院, 吉林 白城 137000)

基于FPGA和STM32的脉宽频率测量方法

潘 宇

(白城师范学院 物理学院, 吉林 白城 137000)

为准确测量高频信号的频率，克服STM32F103输入捕获模式下测得频率最高为80 kHz的缺点。提出用FPGA对高频信号进行分频，用软件编程调整分频因子，将输入高频信号分频到80 kHz以下，然后输入给STM32F103，采用脉宽测量法测得频率。为提高测量精度，采用多次采集，并冒泡排序，去掉部分最大、最小值，用剩余值取均值的滤波算法提高测量频率的精度。最后将测量值与FPGA的分频倍数相乘即可得到实际频率。测试结果表明：该方法实现简单、测量精度高、频率高，有一定的实用价值。

频率测量； 脉宽测量法； 均值滤波算法； 分频

0 引 言

在仪器仪表应用中，经常要检测信号的频率。目前，常用的检测方法有以下几种：① 闸门法，即1 s内测得的信号跳变的次数，由于毛刺等干扰信号，会存在一定的误差。② 等精度测量法，设置2个同步阀门，同时对测量信号和基准信号进行测量，其计数比就是频率比。因为基准信号频率已知，所以乘以频率比就是测量信号的频率。该方法对硬件电路设计要求较高，要求严格同步。③ 测量正脉宽方法，要求正脉宽的占空比已知，一般为50%。测得正脉宽的宽度后乘以2就是周期，对周期取倒数，就可得到频率[1-3]。

以上方法都要用到计数器，计数器的频率与处理器的主频相关。比如STM32F103，其主频达到72 MHz，通过实验测试可知，用捕获正脉宽的方法测试输入信号的频率时，最高只能达到80 kHz。用其他处理器也会遇到这个问题。因此，为了有效提高测量信号的频率，采用对高频信号分频的方法来降低频率，通过FPGA的软件编程实现任意分频。又因为FPGA技术发展迅速，主频最高可以到GHz。因此将FPGA与STM32相结合，可使测量的频率范围大大提高，可达到几十MHz甚至上百MHz。 为了进一步提高测量的精确度，加入均值滤波算法，连续采集100次，然后冒泡排序，将最大值和最小值各去掉20个，用剩余的60个取平均值。这样就可有效去除干扰，大大提高测量频率的精度。

1 系统设计

1.1 设计框图

系统设计框图如图1所示。图中首先对输入的信号分频，分频因子用VHDL编程语言实现。将分频后得到的低频信号输入处理器STM32F103RBT6，采用正脉宽测量法和改进的均值滤波算法测得该信号的频率，将其通过串口送到电脑上显示[4-8]。

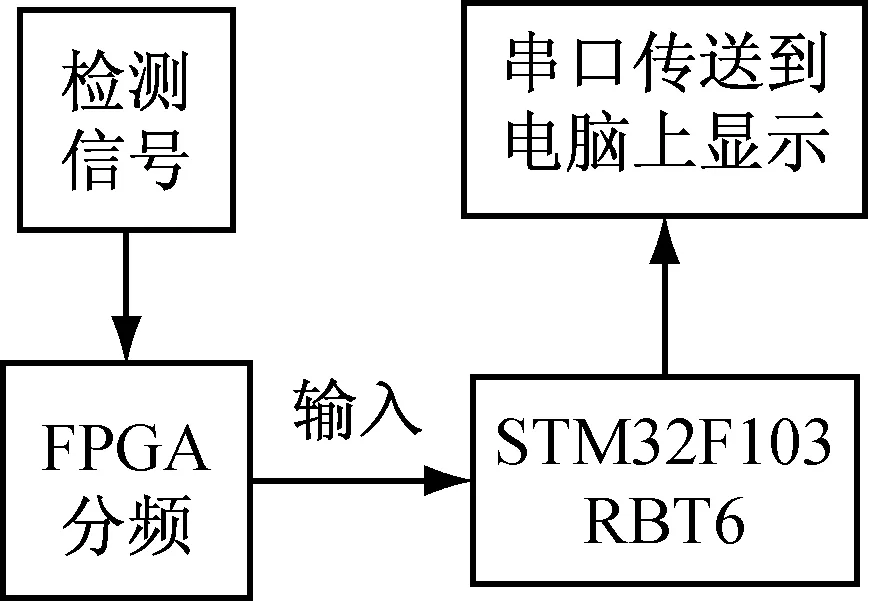
图1 系统框图

1.2 FPGA分频软件设计

将要检测的信号作为输入信号输入FPGA。分频器就是将高频信号进行分频，得到较低频率的信号。分频系数为

(1)

式中:Fin为输入信号频率;Fout为输出信号频率[9-12]。

在VHDL语言程序设计时，定义一个N位的计数器，对输入的时钟脉冲进行计数，计数结果的第N-1位就是对输入时钟的2的N次幂分频。将相应的位数取出即可得到分频时钟。在VHDL下编写的程序代码如下：

LIBRARY IEEE;

USE IEEE.STD_LOGIC_1164.ALL;

USE IEEE.STD_LOGIC_ARITH.ALL;

USE IEEE.STD_LOGIC_UNSIGNED.ALL;

ENTITY test IS

PORT (clk : IN STD_LOGIC;

clk_div2 : OUT STD_LOGIC;

clk_div4 : OUT STD_LOGIC;

clk_div8 : OUT STD_LOGIC;

clk_div16 : OUT STD_LOGIC);

END test;

ARCHITECTURE rtl OF test IS

SIGNAL count:STD_LOGIC_VECTOR(3 DOWNTO 0);

BEGIN

PROCESS(clk)

BEGIN

IF (clk'event AND clk='1') THEN

IF(count="1111") THEN

Count <= (OTHERS =>'0');

ELSE

Count <= count +1;

END IF ;

END IF ;

END PROCESS;

clk_div2 <= count(0);

clk_div4 <= count(1);

clk_div8 <= count(2);

clk_div16 <= count(3);

END rtl;

上述代码可实现2、4、8、16分频。若想实现更高分频，只需要适当的修改参数即可。

1.3 STM32F103软件设计流程图

主控采用STM32F103RBT6，基于Cortex-M3内核，是32位的微处理器。主频为72 MHz，有TIM2、TIM3、TIM4、TIM5共4个通用定时器。每个定时器都有4个独立的通道，这些通道都可以用来作为输入捕获通道使用。在软件编程时使用TIM2的通道1作为检测信号输入端。串口与电脑相互连接，将测得的数值传送到电脑上显示。

软件设计流程图如图2所示， 图中将经过FPGA分频的检测信号接入STM32的TIM2的通道1，首先初始化串口为460800，N,8，1.然后初始化定时器TIM2为输入捕获模式，采用1 MHz的频率计数，测到的计数初值刚好对应的是1 μs，如果测到计数值是10，则为10 μs。当检测到上升沿时启动定时器计数;当捕获到下降沿时，停止计数。

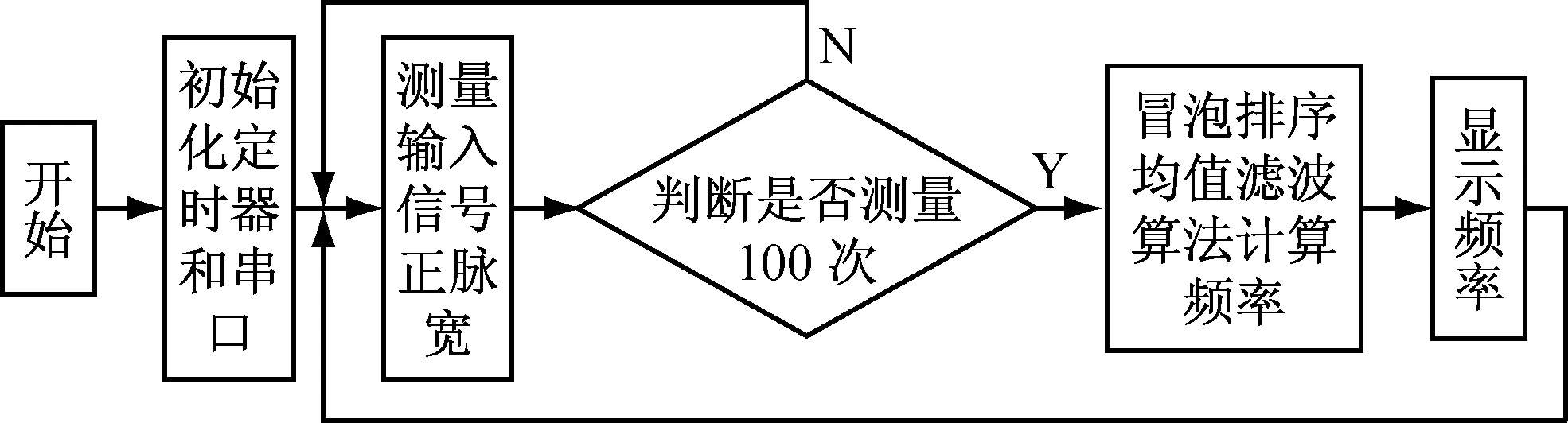
图2 软件设计流程图

1.4 初始化代码

串口初始化代码如下：

void uart_init(u32 pclk2,u32 bound)

{

float temp;

u16 mantissa;

u16 fraction;

temp=(float)(pclk2*1000000)/(bound*16);//得到USARTDIV

mantissa=temp; //得到整数部分

fraction=(temp-mantissa)*16; mantissa<<=4;

mantissa+=fraction;

RCC->APB2ENR|=1<<2; //使能PORTA口时钟

RCC->APB2ENR|=1<<14; //使能串口时钟

GPIOA->CRH&=0XFFFFF00F;//IO状态设置

GPIOA->CRH|=0X000008B0;//IO状态设置

RCC->APB2RSTR|=1<<14; //复位串口1

RCC->APB2RSTR&=～(1<<14);//停止复位 USART1->BRR=mantissa; // 波特率设置

USART1->CR1|=0X200C; //1位停止,无校验位.

if EN_USART1_RX //如果使能了接收

USART1->CR1|=1<<5; //接收中断使能 MY_NVIC_Init(3,3,USART1_IRQn,2);//设置中断优先级

endif

}

定时器2输入捕获初始化程序：

void TIM2_Cap_Set(u16 arr,u16 psc,u8 ch)

{

RCC->APB1ENR|=1<<0; //TIM2 时钟使能

RCC->APB2ENR|=1<<2; //使能PORTA时钟

TIM2->ARR=arr; //设定计数器自动重装值

TIM2->PSC=psc; //预分频器

switch (ch)

{

case 1: //select PA0 GPIOA->CRL&=0XFFFFFFF0; GPIOA->CRL|=0X00000008;

GPIOA->ODR|=0<<0;//PA0 下拉

TIM2->CCMR1|=1<<0;//CC1S=01 TIM2->CCMR1|=1<<4;

TIM2->CCMR1|=0<<2;

TIM2->CCER|=0<<1; /CC1P=0 BIT1=0 上升沿捕获 BIT1=1 下降沿捕获

TIM2->CCER|=1<<0; TIM2->DIER|=1<<1; //允许捕获中断CC1IE：BIT1=1 允许捕获/比较1中断 break;

}

TIM2->DIER|=1<<0; //允许更新中断TIM2->CR1|=0x01; //使能定时器2

MY_NVIC_Init(2,0,TIM2_IRQn,2);

}

捕获部分关键代码：

if(TIM2CH1_CAPTURE_STA&0X80)//成功捕获到了一次高电平

{temp=TIM2CH1_CAPTURE_STA&0X3F;

temp*=65536;

temp+=TIM2CH1_CAPTURE_VAL;//得到总的高电平时间

printf("HIGH:%d us ",temp/72);//打印总的高点平时间

TIM2CH1_CAPTURE_STA=0;//开启下一次捕获

}

对上述代码重复调用100次，得到100次的值，然后冒泡排序，去掉最大值和最小值各20个，用剩余的值求均值，就可得到被测信号的周期，将其乘2取倒数，就可得到频率[13]。

2 测试结果

2.1 FGPA分频测试结果

在Quartus8.0下，用VHDL编程，并设置好相应的参数后，仿真运行，可得到如图3所示[14-16]波形。在图中，对输入信号CLK分别实现了2、4、8和16分频。

图3 分频图

图4所示是经16分频后输入给STM32的80 kHz波形。用示波器测得的频率是80 kHz，由于示波器误差，占空比测得是50.4%，而实际是50%。

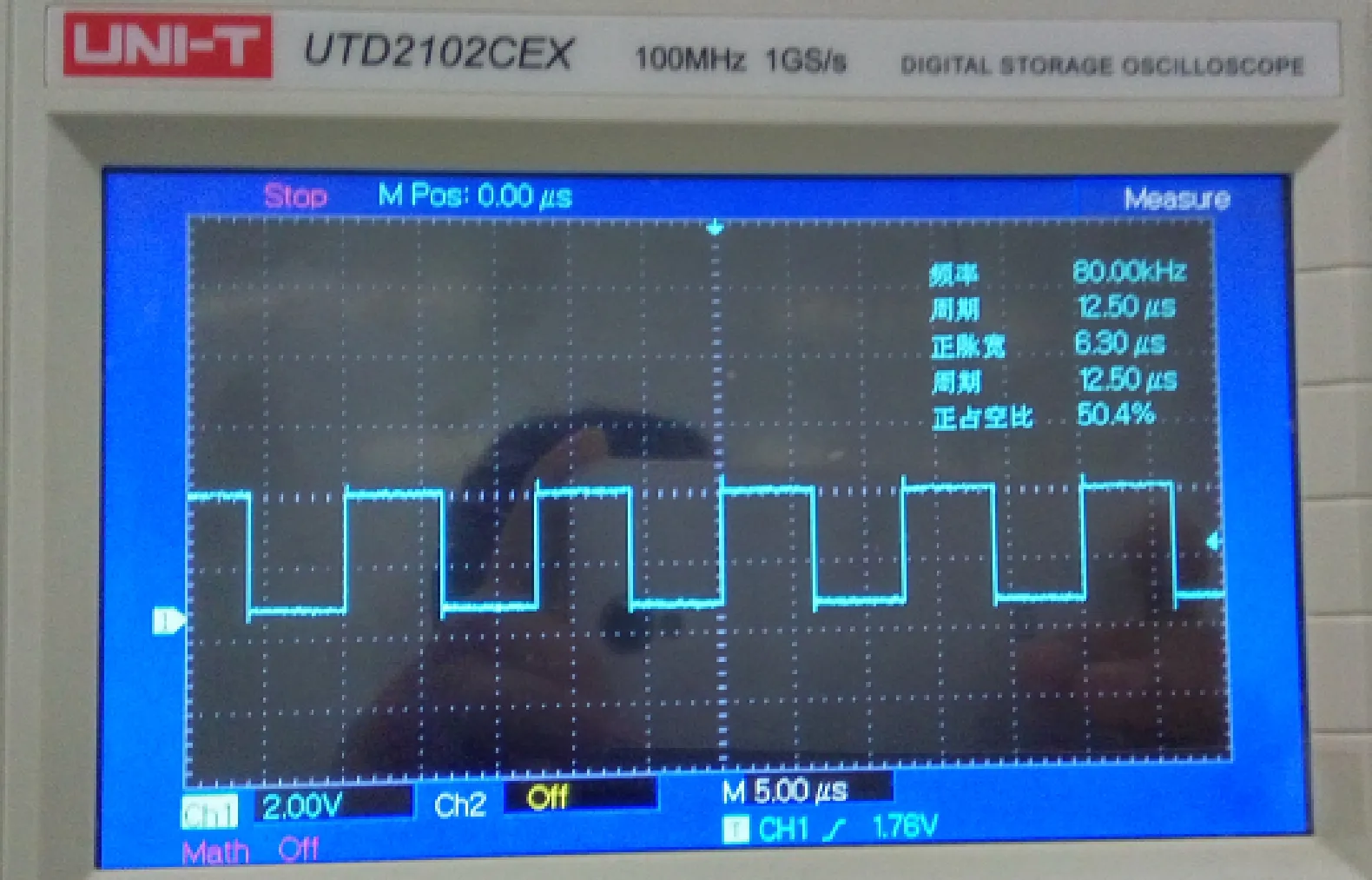
图4 分频后产生的80 kHz波形

2.2 频率测试结果

在Keil下用C语言编程，将80 kHz的方波输入给STM32的PA0，对PA0输入信号进行脉宽测量，并经过改进的均值滤波算法得到的频率，通过串口助手显示结果如图5所示。从图中可以看出，基本上没有误差。实际信号的频率是:80×16=1 280 kHz。

图5 串口显示的测量频率

3 结 语

本文提出了一种频率检测的新方法，为有效提高检测频率的范围，采用高速FPGA软件编程分频的方法，将高频信号频率降低为低频信号。输入给STM32，利用STM32定时器的捕获功能测量正脉宽的宽度，以此得到信号的周期，对其求倒数及得到频率。为有效提高测量的精度，采用改进的均值滤波算法，经多次测量排序，并去除干扰比较大的数值后求均值，提高了测量的精度。经测试，该方法能够有效提高测量频率的范围，可测量较高的频率，并且精度较高，有一定的实用价值。

[1] 应毓海. FPGA 高精度测量频率研究[J].低温与超导,2014,42(3):79-82.

[2] 陈寿法，王中鹏. 等精度频率测量的同步门电路改进设计[J]. 电测与仪表,2015,52(18): 90-95.

[3] 张天恒，叶 伟. 基于SOPC的便携式高精度频率仪设计[J].仪表技术与传感器,2015(5):34-37.

[4] 江 修,经亚枝,张焕春.用等精度测频方法实现振弦式传感器频率测量[J].传感器技术,2001,20(6):53-55.

[5] 黄国刚,陈 明,张 朋.声表面波CO气体传感器高精度频率测量研究[J]. 计算机测量与控制,2009,17(6):1033-1038.

[6] 沈 伟,王军政,汪正军.一种基于信号补偿的频率测量方法[J].仪器仪表学报,2010,31(10):2192-2197.

[7] 刘 娅, 李孝辉, 王玉兰. 一种基于数字技术的多通道频率测量系统[J]. 仪器仪表学报,2009,30(9):1963-1968.

[8] 汪正军，潘 磊，纪国瑞. 基于离散相位差检测的频率测量方法[J]. 仪器仪表学报,2013,34(5):994-999.

[9] 梁文海,麦 文,张 健,等. 一种高精度频率测量的研究与实现[J]. 四川师范大学学报(自然科学版),2008,31(3): 376-378.

[10] 牟龙华,邢锦磊. 基于傅里叶变换的精确频率测量算法[J].电力系统自动化,2008, 32(23):67-70.

[11] 杜玉环，郭迎清.基于LabVIEW的FFT光纤涡轮流量测量系统研究[J].仪表技术与传感器,2015(11):56-58.

[12] 闫 珺, 王淑红. 一种基于软件锁相环的电网频率动态检测方法[J]. 电测与仪表,2015,52(24): 56-59.

[13] 李月琴，裴 丽.多级高精度可调谐的瞬时频率测量方法[J].中国激光，2015,52(24): 1-8.

[14] 孟 卓，温 和. 基于复化梯形的准同步采样频率测量算法[J]. 中国电机工程学报,2015,35(10): 2445-2453.

[15] 易 艺，岳庆英.基于FPGA的便携式课外实验仪设计与实现[J]. 实验技术与管理,2016,33(1): 86-90.

[16] 薛海东, 郭迎清.基于DSP的高精度测频方法与软件设计[J]. 传感器与微系统,2016,35(1): 117-120.

Pulse Width Frequency Measurement Method Based on FPGA and STM32

PANYu

(Department of Physics, Baicheng Normal College, Baicheng 137000, Jilin， China)

In order to accurately measure the frequency of high frequency signals, overcome the shortcomings of the highest measured frequency is 80 kHz under the STM32F103 input capture mode. The paper proposed to use FPGA to divide the high frequency signal, and use software to adjust the factor of frequency division, the input high frequency signal can be divided and every component is below 80 kHz, then STM32F103 can measure them. In order to improve the measurement precision, we apply the repeated acquisition and bubble sorting, and then remove the maximum and minimum values, and take the average for the remaining values. The method improves the accuracy of frequency measurement. Finally, the measured value can be multiplied with the frequency division of FPGA to get the actual frequency. The test results show that the method is simple and has high precision and high frequency, it has certain practical value.

frequency measure； pulse width measurement； average filtering algorithm; frequency division

2016-05-12

潘 宇 (1982-), 男, 吉林白城人，硕士,讲师, 主要研究方向：电子信息工程。

Tel.：15590795511; E-mail: 82048492@qq.com

TP 216

A

1006-7167(2017)02-0083-04