四容水箱实验装置数学模型的特点分析

何豫溪， 冀学青， 朱兆霞， 邹 斌

(1. 上海大学 机电工程与自动化学院， 上海 200072； 2. 上海博杰科技有限公司， 上海 201399)

四容水箱实验装置数学模型的特点分析

何豫溪1， 冀学青1， 朱兆霞2， 邹 斌1

(1. 上海大学 机电工程与自动化学院， 上海 200072； 2. 上海博杰科技有限公司， 上海 201399)

为研究一个高阶、非线性且其零点可在S的左右平面移动的四容水箱系统以及为该系统的控制实验方案的设计提供基础，通过建立不同阀门关断/开启的水箱系统的状态方程、传递函数矩阵等数学模型，讨论了模型的结构特征；通过研究阀门开度变化对系统零极点位置的影响，揭示了四容水箱系统的数学模型特点。结果表明，调整水泵的开断及阀门开度可方便地构成MIMO和SISO系统，泰勒级数展开的初始条件不同模型的特点不同，系统零点在S左右平面上分布取决于水泵阀门开度γ1+γ2，改变阀门开度，特别是互联阀门的开度可以改变零极点位置，进而影响控制方案的设计。

四容水箱控制； 数学模型； 零极点位置； 泰勒级数展开

0 引 言

水箱液位控制系统因其具有工业环境中时常出现的强耦合性、非最小相位以及非线性等特点，且实现相对简单经济，一直以来是较为理想的实验设备[1-4]。

水箱液位控制系统的对象经历了两水箱、三水箱和四水箱系统的演变。Johansson[5]提出了一种四水箱液位控制系统，该系统最大的特点是其零点可通过调节水泵阀门开度而在S左右平面移动，使系统表现出最小相位系统和非最小相位系统的特点。文献[6]中在底层2个水箱之间增加了一条水管连接，使得四水箱液位系统具备了更加丰富的特征。

四容水箱实验对象提出以后立即引起了学术界和大学实验教学方面的广泛注意[7]以及相关实验装置的研究。李志军等[8]介绍了其研制的四水箱控制系统方案；刘洋[9]则介绍了四水箱控制的数学模型及其解耦控制；王资法等介绍了其基于四水箱系统完成的控制方案的设计[10]；陈培颖等[11]完善了逆解耦器的设计策略并将其应用于水箱模型。Johansson[12]设计了分散PI控制器进行控制， Garrido等[13]采用IDC-IMC对四容水箱模型进行了仿真研究。

四容水箱控制系统随着其运行参数的改变具有丰富的特点，表现在数学模型上则是其数学模型的结构和参数会随相关设置的改变而改变。系统认识四水箱系统的这些特点对基于该装置的实验开发具有重要意义，本文将全面系统地研究四水箱控制系统的特征。

1 四容水箱系统的物理模型

四容水箱互联系统物理模型如图1(a)所示，左右两边的水泵1和2把水从蓄水池送到4个水箱，水泵1供给水箱1的进水孔阀门开度为γ1，水泵2供给水箱2的阀门开度为γ2。在高位的水箱3的出水孔通过阀门R3将水排到低位的水箱1，水箱4通过R4将水排到水箱2，水箱1和2通过阀门R1和R2将水排至底部大的蓄水池中，水箱1和2之间的连通孔通过阀门Rx进行联通。

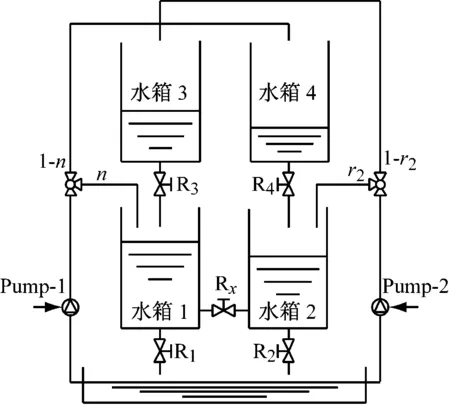
(a)四容水箱物理模型

(b)阀门参数调整后的物理模型

四容水箱的被控量是水箱1和2的液位，控制量是水泵1和2的输入电压u1和u2。一般而言，四容水箱系统是一个4阶的包含零点的系统。

通过调整水泵阀门1和2对上水流量比例的分配以及关断下水阀门和互通阀门的方式改变水的流通路径，还可以形成不同的特点的受控模型。例如，上水水泵2停机，上水阀门1全部将水流送到水箱4，也即γ1=0，且联通阀门Rx开通，此时水的流通路径如图1(b)所示，若仅研究水箱2液位的变化，则此时的系统为一个包含一个零点的单入单出的3阶系统。

此外，通过调整水泵阀门的开度可改变原四容水箱互联系统零点位置在S左右平面的分布，从而改变受控对象的性质使其具有不同的最小相位和非最小相位的特征。另外，系统随时间变化而有不同的响应，从而也可获得时变系统的特性。

2 四容水箱系统的数学模型

2.1 四容水箱系统的非线性数学模型

根据物料守恒原则及伯努利法则，可写出系统的微分方程：

(1.a)

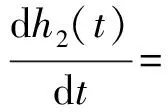
(1.b)

(1.c)

(1.d)

式中：A指水箱的横截面积(cm2)；ai指水箱i出水孔的横截面积(cm2)；ax指水箱1和2之间连通管道的横截面积(cm2)；hi(i=1,2,3,4)指水箱i的液位高度(cm)；uj(j=1,2)指水泵j输入电压(V)；βj(j=1,2,3,4)指水箱i的出水孔Ri的阀门开合比例；βx指水箱1和2连接管道的阀门开合比例；γj(j=1,2)指上水阀门j流入下水箱的比例；kpj(j=1,2)指水泵j的增益(cm3/(V·s))；g指重力加速度(981 cm/s2)。

式(1)给出了水箱液位hi(i=1,2,3,4)与水泵输入电压uj(j=1,2)之间的非线性关系。这种关系与水泵的增益、水箱的截面积和水箱出水孔及连通孔的横截面积有关，这类参数在实验装置制造完成后便固定了，为常数。影响输入输出之间关系的还有上水阀门进入水箱的比例γj(j=1,2)、各个水箱下水阀门的开度，βj(j=1,2,3,4)和水箱1和2连接管道的阀门开合比例βx。这类参数是可以在运行中改变的，不同的运行参数对输入输出关系的影响体现该设备的特点。

2.2 四容水箱系统数学模型的线性化

(2)

式中：xi(i=1,2,3,4)为线性化后的各水箱的液位；Ti(i=1,2,3,4)和Tx为时间常数，它们的表达式如下：

基于状态方程，易于求得其传递函数矩阵[15]为

(3.a)

(3.b)

(3.c)

(3.d)

(3.e)

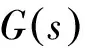
2.3 四容水箱系统SISO的数学模型

四容水箱系统可以通过关闭上水和下水阀门以及连通孔阀门而形成不同的流体传输通路,获得不同的数学模型。当将阀门关断形成图1(b)所示的水流路径时，则形成了一个含零点的3阶SISO系统。在图1(b)的基础上将连通孔阀门关断，则形成了一个2阶不含零点的系统。为节省篇幅，本文仅给出图1(b)所示系统的数学模型。此时系统的传递函数矩阵及其元素的表达式如下式所示：

(4.a)

(4.b)

(4.c)

R=T1T2Txs2+2T1T2s+T1Txs+T2Txs+T1+T2+Tx

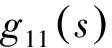
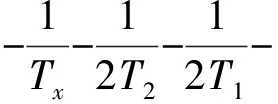
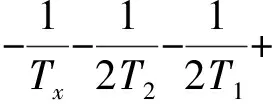
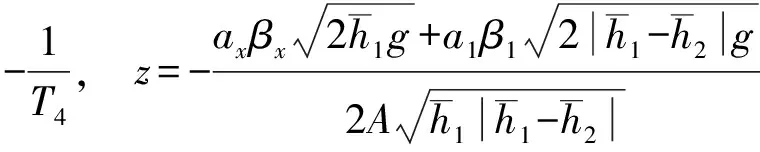
3 四容水箱系统的参数影响分析

基于MIMO和SISO系统的数学模型，不同运行参数可获得不同数学模型，形成不同特点的受控对象。

3.1 初始液位高度的影响

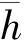
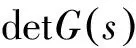
(1) 液位初始位置的变化不会引起零极点的位置发生质的变化，在零极点全是负数时，一直保持负数不变。

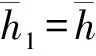
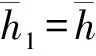
(4) 高位水箱初始液位高度对系统传递函数零极点的影响作用相对底层水箱要小。

图2 hi对MIMO系统极点位置分布的影响 图3 hi对MIMO系统零点位置分布的影响

3.2 出水孔及连通孔阀门开度的影响

四容水箱的出水孔的阀门开度βj通过影响对应水箱的时间常数Ti，连通孔的阀门开度βx通过影响Tx，进而影响水箱系统的零极点位置在S平面上的分布。βj对极点位置分布影响的作用曲线如图4所示，对零点影响的曲线如图5所示。

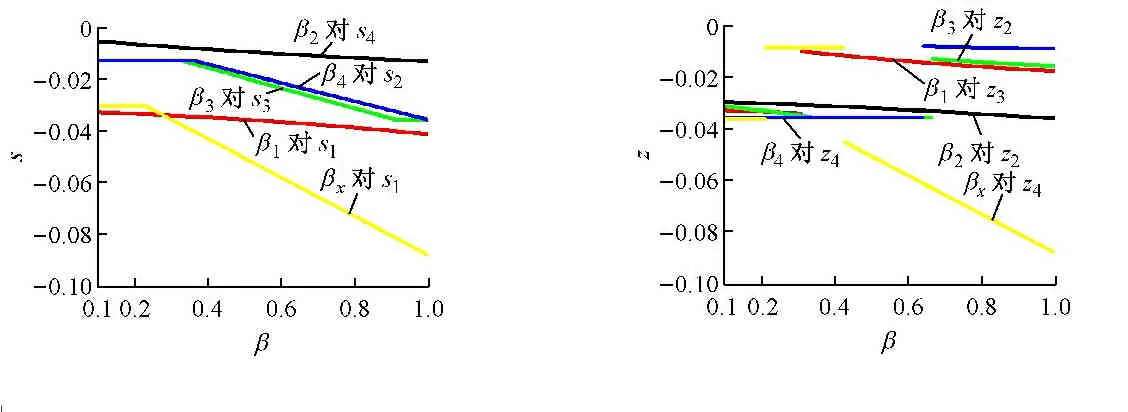
图4 βj对MIMO系统极点位置分布的影响 图5 βj对MIMO系统零点位置分布的影响

(1) 阀门开度的变化不会引起零极点的位置发生符号上的变化。

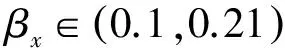
(3) 随着出水孔或连通孔的阀门开度渐大，单一阀门开度影响下的传递函数的极点或是保持不变或是向偏离原点的方向移动，这为后续控制器的设计提供了方便。

(4) 互联阀门开度对系统零极点位置的影响是所有阀门开度中影响最为显著的一个。

3.3 水泵阀门的开度的影响

四容水箱的水泵阀门开度γ1、γ2通过影响系统线性状态空间表达式中的输入矩阵B，进而影响系统的零极点位置在S平面上的分布。γ1、γ2对极点位置分布影响的作用曲线如图6所示，对零点影响的曲线如图7所示。

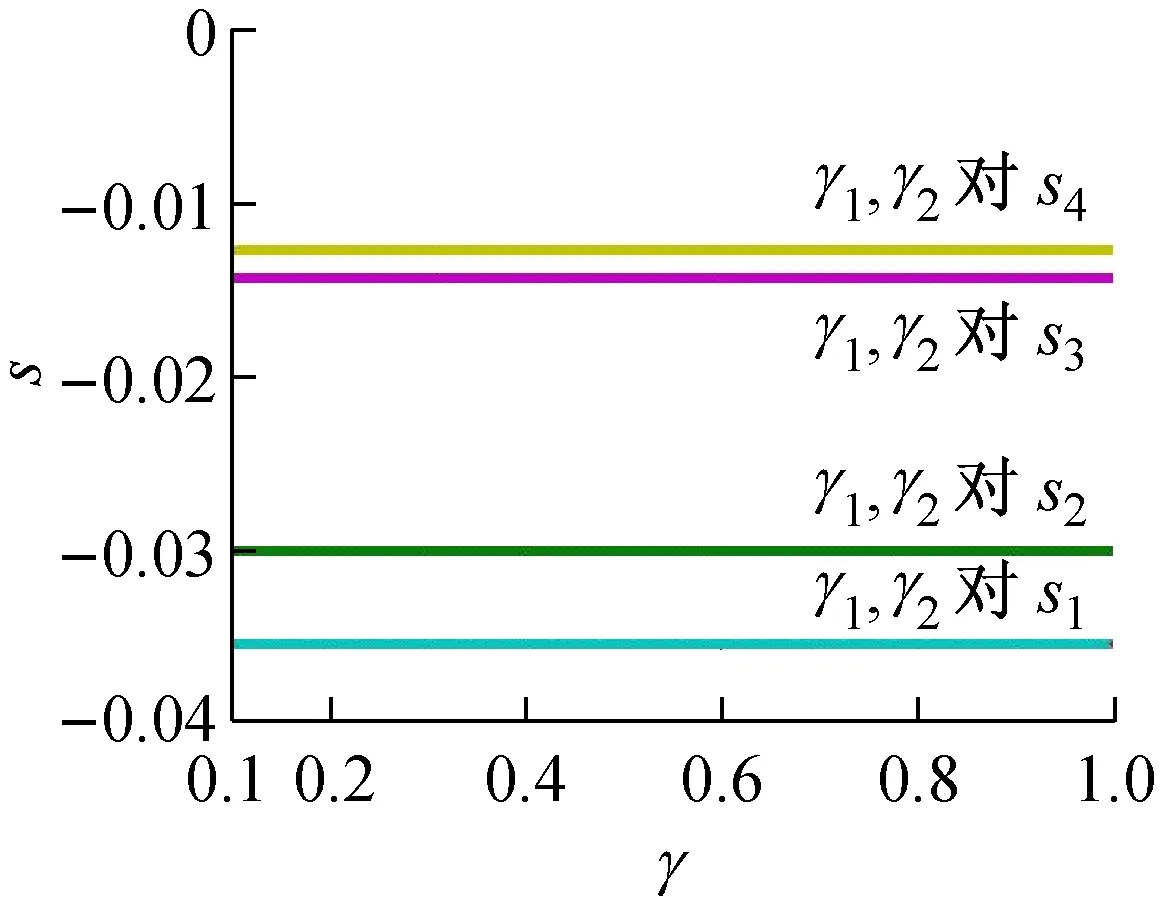
图6 γ1、γ2对MIMO系统极点位置分布的影响

(1) 由图6可见，si不随γ1，γ2的变化而变化，故γ1、γ2不对系统极点的分布产生影响。

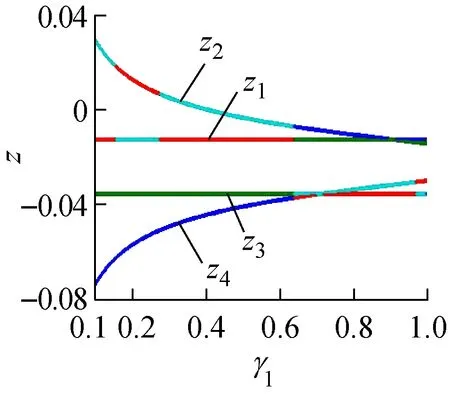
(2) 由图7可见，γ1、γ2对系统零点的分布产生较为显著的影响，在γ1和γ2逐渐变化过程中，系统不仅存在S左半平面的零点，同时也存在S右半平面的零点。当系统出现原点处的零点时，此时对应γ1+γ2=1。

由图8可见：在0<γ1+γ2<1时，系统既有S左半平面的零点，又有S右半平面的零点，此时的系统为非最小相位系统；在1<γ1+γ2<2时，系统仅有S左半平面的零点，为最小相位系统；在γ1+γ2=1时，系统的零点中包含S平面的原点。因此通过该实验装置，可以通过调节γ1、γ2得到不同的系统特性，并且该特性能够得到较为直观的物理解释。

图8 γ1+γ2对零点位置分布的影响

3.4 SISO三阶带零点的参数影响分析

与上述分析类似，下面讨论参数对SISO系统的影响。

(1) 初始液位高度的影响。初始液位高度对部分极点位置分布影响的作用曲线如图9所示，对零点影响的曲线如图10所示。

图i对SISO系统极点位置分布的影响

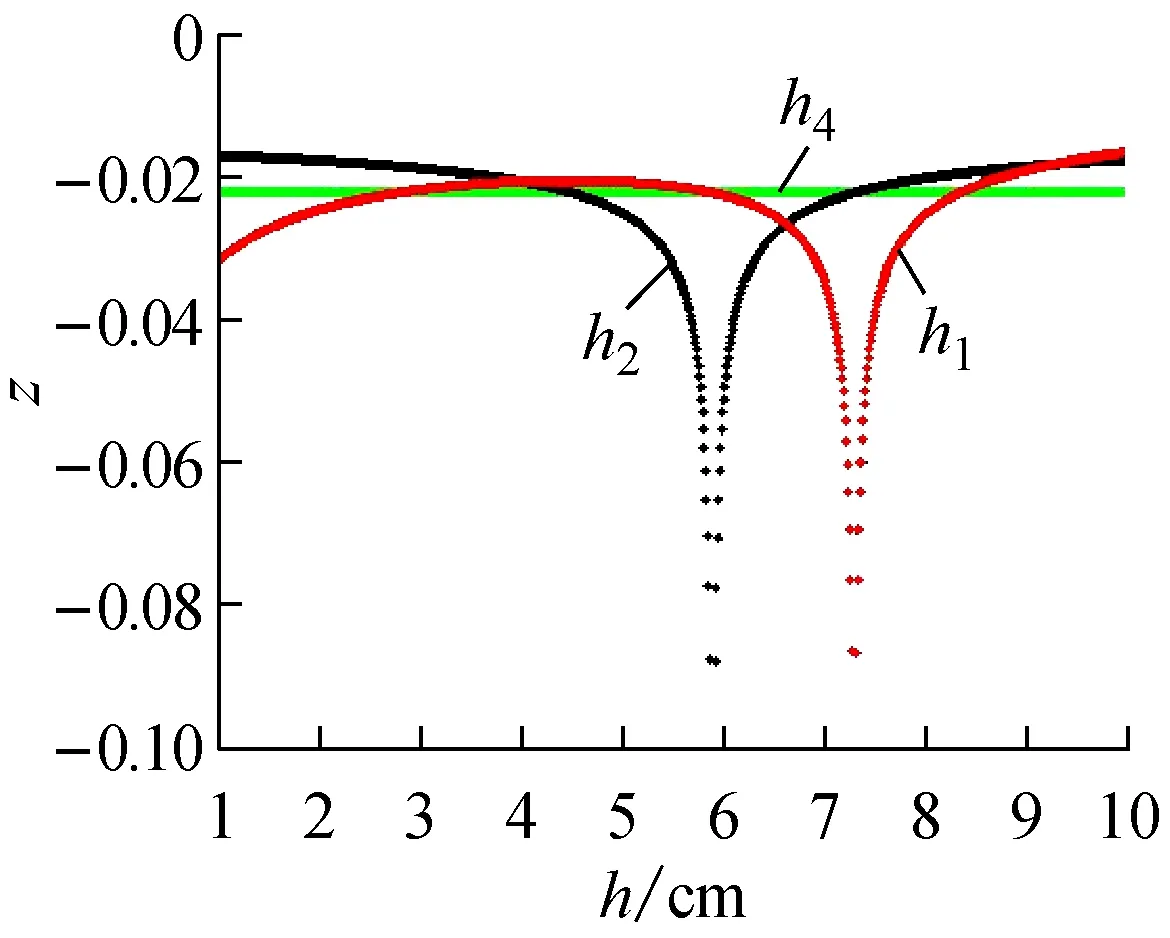
图对SISO系统零点位置分布的影响

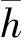
② 水箱4的初始液位发生变化时，会影响s3，但不会对零点位置的分布造成影响。

(2) 出水孔及连通孔的阀门开度的影响。βj对极点位置分布影响的作用曲线如图11所示，对零点影响的曲线如图12所示。

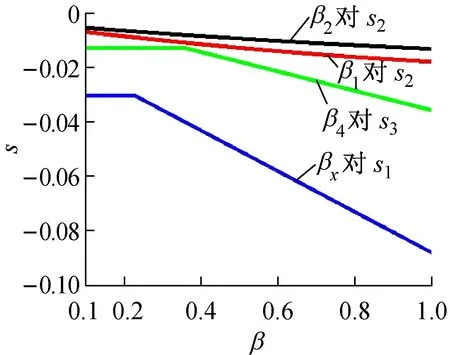
图11 βj对SISO系统极点位置分布的影响

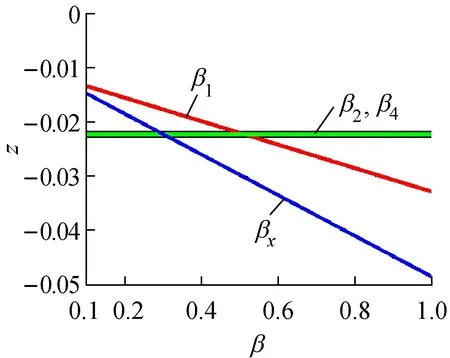
图12 βj对SISO系统零点位置分布的影响

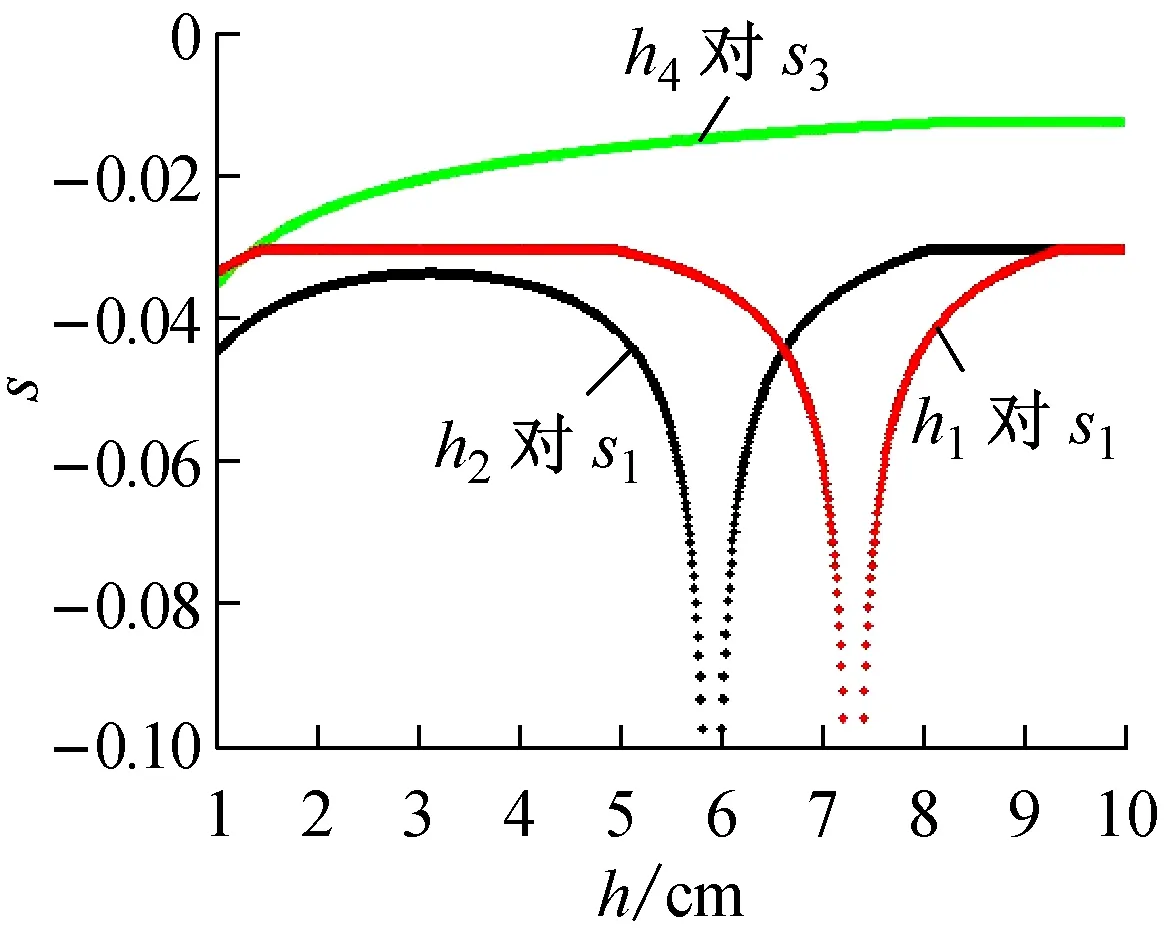
① 当水箱1和水箱2的出水孔阀门开度变化时，s1和s2随之变化，而s1相对s2的变化速率缓慢，故在图11中仅绘制出β1和β2变化对s2的影响。此外，β1通过影响T1而对z产生影响，而β2不影响系统零点的位置分布。

② 当水箱4的出水孔阀门开度变化时，s2和s3随之变化，而在图11中仅绘制出β4对s3的影响曲线。因SISO系统零点的表达式中不含与β4相关的量，故β4不影响零点的位置分布。

③ 水箱1和2之间连通孔的阀门开度影响s1、s2和z，且对系统零极点位置的影响是所有阀门开度中影响最为显著的一个。

通过上面的分析，知道运行参数的不同会对系统的零极点分布产生影响，而零极点分布又与控制系统的性能相关。图13反映了运行参数βx对系统阶跃响应曲线的影响。

当βx由0.3增大到0.7时，系统零极点与原点间的距离均有所增大，系统的稳定性不变，系统的稳态值(稳态时水箱2的液位)由2.84 cm降至2.55 cm，系统的时间由177 s升至189 s。

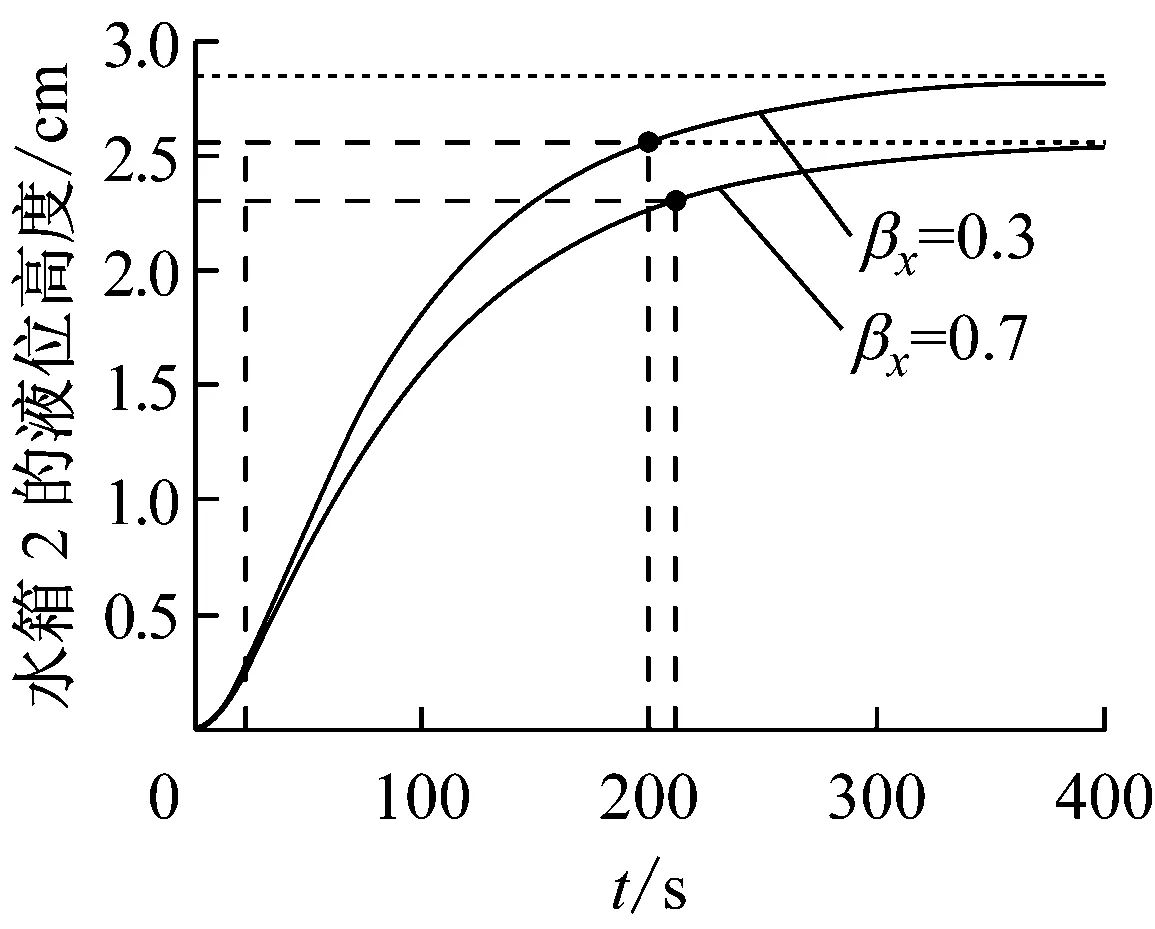
图13 βx对系统阶跃响应的影响

4 结 论

四容水箱系统可以通过调节水箱初始液位高度和阀门开度的大小而形成具有不同结构和参数受控的对象，为自控实验提供了丰富的受控对象。具体表现为：

(1) 通过上水阀门开度的变化，系统极点的位置不变但零点随之在S平面的左右侧移动而具有最小相位和非最小相位的特征，因此可以方便地比较这两种系统的特点。

(2) 改变四容水箱系统初始液位高度会改变系统的零极点，为控制系统非线性系统线性化提供了方便的实验手段。其中，水箱1和2的初始液位较为接近时，其变化对零极点的影响较为显著，水箱3和4则对最靠近原点的零极点影响显著。利用该特点，可以设计出非线性系统线性化对模型的影响的实验方案。

(3) 改变水箱系统下水阀门及互联阀门的开度会改变系统的零极点。其中，互联阀门的影响对系统零极点影响最为显著。可以通过改变改阀门获得不同参数的系统，并进而进行不同的控制器参数的整定。

[1] 王华忠,孙自强.基于智能仪表和PLC的双容水箱测控实验系统开发[J].电气电子教学学报,2009,31(z2):1-3.

[2] 何 潇,王子栋.基于Internet的网络化三容水箱实验平台[J].南京航空航天大学学报,2011,43(S):190-193.

[3] 朱春燕,刘文泉.液位控制系统实验台的研制[J].国外电子测量技术,2012,31(2):91-93.

[4] 叶希立，丁 强，黄国辉，等. 三容水箱计算机控制仿真与实验系统的研发[J]. 实验室研究与探索, 2013, 32(6): 81-83,96.

[5] Johansson K H. The Quadruple-Tank Process: A Multivariable Laboratory Process with an Adjustable Zero[J]. IEEE Transactions on Control Systems Technology, 2000, 8(3): 456-465.

[6] Numsomran V， Tipsuwanporn K Tirasesth. Modeling of the Modified Quadruple-Tank Process[C]∥SICE Annual Conference 2008， The University Electro-Communications, Japan：August 20-22, 2008.

[7] Siddharth Dadhich, Wolfgang Birk. Analysis and Control of an Extended Quadruple Tank Process[C]∥2014 European Control Conference (ECC), Strasbourg, France:June 24-27, 2014.

[8] 李志军，贺 庆，郭富民. 多变量四容水箱控制系统实验装置的设计[J]. 制造业自动化，2013,35(5): 122-125.

[9] 刘 洋. 四水箱控制系统的建模与解耦分析[J]. 沈阳航空工业学院学报, 2007, 24(5): 73-75.

[10] 王资法, 张 湜, 薄翠梅.四水箱控制系统的性能评价[J]. 计算机工程与科学, 2011, 33(2): 164-167.

[11] Chen P, Zhang W. Improvement on an inverted decoupling technique for a class of stable linear multivariable processes[J]. Isa Transactions, 2007, 46(2):199-210.

[12] Johansson K H. Interaction bounds in multivariable control systems[J]. Automatica, 2002, 38(6):1045-1051.

[13] Garrido J, Vázquez F, Morilla F. An extended approach of inverted decoupling[J]. Journal of Process Control, 2011, 21(1):55-68.

[14] 肖 建，张友刚.线性系统理论[M].成都：西南交通大学出版社，2011：19-60.

[15] 胡寿松.自动控制原理[M]. 6版.北京：科学出版社，2013：201-237.

Analysis of the Mathematical Model of Quadruple-tank Experimental Apparatus

HEYuxi1，JIXueqing1，ZHUZhaoxia2，ZOUBin1

(1. School of Mechatronic Engineering and Automation, Shanghai University, Shanghai 200072, China; 2. Shanghai Brotek Co., Ltd., Shanghai 201399, China)

In order to analyze a high-order, nonlinear typical system in industrial process with a zero that can be located either in the left-half or right-half complex plane, a quadruple-tank system was selected an research objective. By different situations of valves, different state-space equations and transfer function matrices and other mathematical models could be obtained. The features of these models were discussed. The openness and close, and opening rates would lead to different positions of zeros and poles. The results showed that it was convenient to build MIMO or SISO systems by adjusting the pump state and valve ratio. The model features were different with different initial conditions in Taylor series expansion. The zero locations depended onγ1+γ2the opening ratio of valves. Changing the valve radios, especially the connection valve would affect the zeros and poles location and system characteristics, so were the control schemes.

quadruple-tank control; mathematical model; locations of poles and zeros; Taylor series expansion

2016-06-02

何豫溪(1994-)，女，河南周口人，硕士，主要研究方向为电气工程。

Tel.:18817392910；E-mail:18817392910@126.com

邹 斌(1965-)，男，湖北武汉人，教授，博士生导师，主要研究方向为电力市场、定价和电源规划。

Tel.:13122601880； E-mail:zoubin@shu.edu.cn

TP 23

A

1006-7167(2017)02-0044-06