钢筋混凝土保护层锈裂行为的细观有限元模拟

徐亦冬 郑颖颖 杜 坤 胡 雷

(1浙江大学宁波理工学院, 宁波 315100)(2杭州交通投资建设管理有限公司, 杭州 310015)(3重庆交通大学土木工程学院, 重庆 400074)

钢筋混凝土保护层锈裂行为的细观有限元模拟

徐亦冬1郑颖颖2,3杜 坤3胡 雷3

(1浙江大学宁波理工学院, 宁波 315100)(2杭州交通投资建设管理有限公司, 杭州 310015)(3重庆交通大学土木工程学院, 重庆 400074)

为了研究混凝土材料非均匀特性对保护层锈裂行为的影响,基于蒙特卡罗方法建立了随机骨料模型,采用Matlab软件编写了骨料生成和投放代码,并考虑了界面层的影响.通过改变锈蚀层厚度,对钢筋锈胀引发的混凝土保护层开裂行为进行了细观有限元模拟.结果表明,混凝土内钢筋锈蚀产物膨胀具有非均匀性,砂浆与骨料的界面是钢筋混凝土保护层锈胀过程中的最薄弱环节.当锈蚀层的最大厚度为1.24 μm时,界面开始产生裂缝,随后钢筋周围砂浆产生裂缝;当锈蚀层的最大厚度为9.00 μm时,混凝土保护层表面出现裂缝,此时钢筋的有效锈蚀率仅为0.186%;当锈蚀层的最大厚度达到18.00 μm时,混凝土中钢筋之间裂缝贯通,此时裂缝分布图与实测锈胀开裂相似,表明细观模拟计算可靠.

钢筋锈蚀;锈胀开裂;细观模拟;随机骨料模型

氯盐侵蚀引起的钢筋脱钝锈蚀、混凝土保护层开裂和构件承载力下降是造成沿海基础设施耐久性失效的主要因素.随着数值模拟技术的不断发展,有限元模拟已成为材料科学与结构工程学科不可或缺的研究手段,如何有效地模拟沿海混凝土结构的锈裂行为成为了研究的热点.邱兆国等[1]基于混凝土塑性损伤理论,建立了钢筋混凝土保护层锈胀开裂的有限元模型,探讨了钢筋直径、锈胀系数、保护层厚度对临界锈蚀率的影响.韦俊等[2]和Chen等[3]利用有限元软件模拟了钢筋不均匀锈蚀引起的混凝土保护层开裂过程.Guzmán等[4]将内嵌黏结裂纹二维单元用于混凝土锈胀开裂过程的模拟中,并与实际桥梁工程测试数据进行了对比验证.

混凝土是一种由骨料、砂浆及连接两者之间的界面组成的具有复杂力学性质的非均匀准脆性材料.其宏观尺度表现出的性能劣化是内部细观结构损伤不断累积的结果.在研究混凝土结构材料力学性能的过程中,往往只从宏观角度来考虑,忽略了对其内部复杂细观结构的研究,因而传统有限元模拟无法表征混凝土服役过程所表现出的复杂性.通过建立混凝土细观有限元模型,不仅可以反映混凝土材料组成及力学性质的非均匀性,还能利用计算机的高效性来准确分析并得到混凝土破坏的实质[5].

本文基于蒙特卡罗法建立了混凝土随机骨料模型,利用Matlab软件编写骨料生成和投放代码,结合有限元分析软件Abaqus对生成的混凝土细观有限元模型进行网格划分,并考虑了界面层的影响.根据建立的二维细观混凝土模型,通过控制锈蚀层厚度,模拟研究了钢筋锈蚀导致的混凝土保护层开裂过程,并与实测结果进行了对比.

1 细观随机骨料模型

1.1 基本原理

Fuller级配将混凝土骨料有规则地按粒度大小进行组合排列,使其成为密度最大、空隙最小的混合物.Walraven等[6]基于概率统计理论,给出了Fuller三维级配曲线平面转化公式,即

(1)

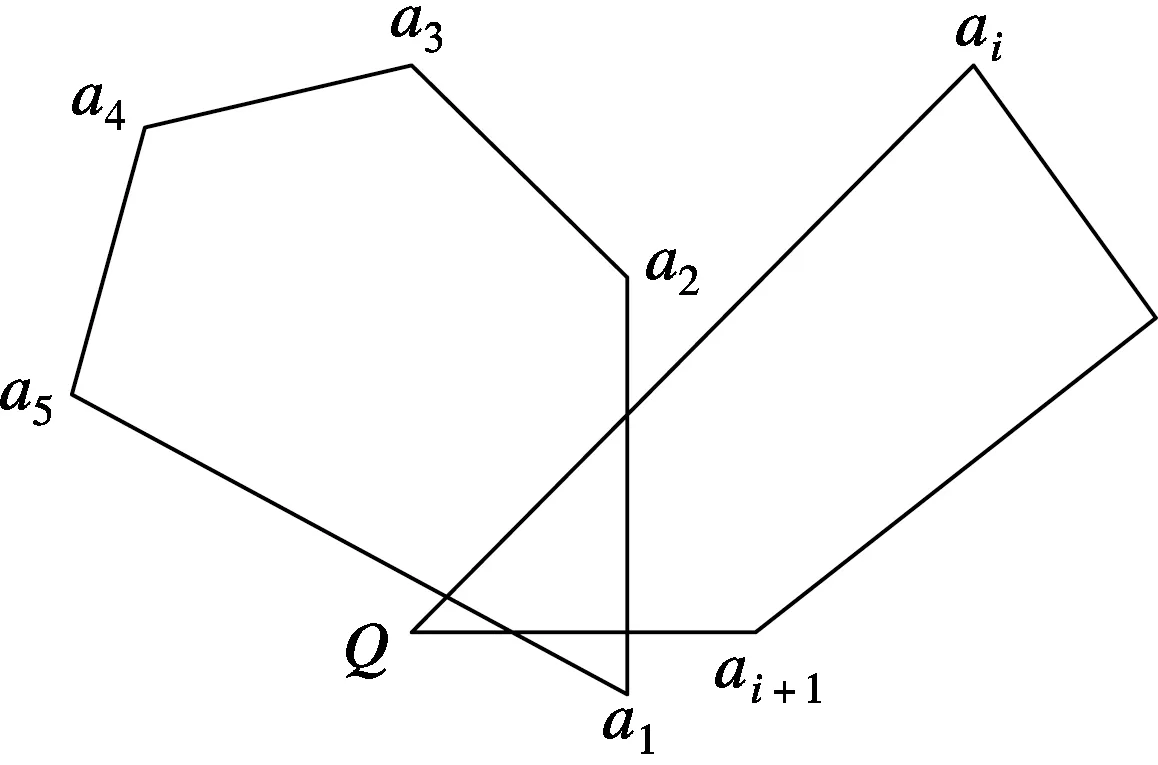
式中,P(D

利用式(1),根据不同的D0取值,可得出概率分布曲线,进而求得内截平面上各种粒径的骨料颗粒数;然后,基于蒙特卡罗法[7],按照骨料之间不重合的原则,对骨料进行随机投放.

1.2 骨料颗粒的生成投放

1.2.1 二维圆形骨料

本文所用的混凝土配合比为m(水泥)∶m(水)∶m(砂子)∶m(粗骨料)=1∶0.53∶2∶3,构件截面尺寸为100 mm×100 mm,试件粗骨料为一级配,骨料粒径为5～20 mm.假定粗骨料形状为球形,据混凝土配合比求出骨料体积分数φ=71%.由式(1)计算出粒径小于D0的骨料在内截平面内出现的概率,结果见表1.分别计算了3个粒径范围(5～10 mm,10～15 mm,15～20 mm)内粗骨料的总面积,取代表性粒径为平均粒径,进而求得二维内截平面内圆形骨料颗粒的数量,结果见表2.

表1 粒径小于D0的骨料在内截平面内出现的概率

表2 圆形骨料颗粒数量

圆形骨料在二维平面上的大小和位置是通过半径和圆心平面坐标参数来控制的,利用Matlab软件中的Rand函数随机生成这3个控制参数.根据骨料之间不能相交、不能重合、不能互相包含的原则[8],确定骨料模型,直到生成指定数目的骨料个数后进行绘图,结果见图1.

图1 圆形骨料的随机生成与投放模型

1.2.2 二维凸多边形骨料

真实碎石骨料的形状多为凸多面体,因此在二维平面模型中采用凸多边形模拟碎石骨料更为合适.采用边延拓法[9-10]生成二维凸多边形随机骨料,具体步骤如下:

① 指定投放区域和粒径区间.在投放区域内生成随机圆,随机圆控制了多边形的大小及位置.

② 在每个随机圆上生成3个点,连接成三角形,并控制每个三角形的余弦值都大于0,使生成的三角形为锐角三角形.

③ 将三角形作为基础向外延伸,以三角形中最长边为直径画圆,圆上生成多边形中新的顶点Q,其坐标为

(2)

式中,xi,xi+1,yi,yi+1为与点Q相邻两点的坐标;laiai+1为三角形最长边的长度;m,n为0～1之间的随机数.为了保证生成的点Q落在三角形的外部,需满足

(3)

式中,S为点Q与点ai、点ai+1围成的三角形面积,S的正负值由点Q、点ai、点ai+1的排列顺序决定,逆时针为正,顺时针为负,可以通过控制S的正负值来决定节点的顺序.为了保证骨料的凸形,控制点Q离基骨料圆心的距离小于骨料2倍粒径.

④ 进行颗粒相交检查.计算骨料最大粒径,如果2颗骨料中心之间的距离大于其最大粒径之和,则骨料不相交;否则,运用克莱姆法则判断是否存在交点,如果存在交点,则剔除该延伸点(见图2).

图2 颗粒相交时情形

⑤ 重复步骤①～④,即可生成满足设定参数的多边形随机骨料模型.

利用上述二维凸多边形随机骨料生成方法,建立了尺寸为100 mm×100 mm,φ=71%,骨料粒径为5～20 mm的随机骨料投放图(见图3).

1.3 界面层的生成

界面层本质上是一层含较高孔隙率的近场砂浆材料,其孔隙率和水灰比远大于离骨料较远的砂

图3 二维凸多边形随机骨料骨料模型

浆,强度在混凝土组分中最低.界面层厚度一般为10～50 μm,为兼顾计算精度与运算成本,通常使界面层厚度取值偏大,如文献[11]分别选取了0.3与0.5 mm两种界面层厚度进行计算.本文将Matlab软件生成的随机骨料模型导入到AutoCAD软件中,并利用AutoCAD软件提取随机骨料模型边界参数,在骨料表面添加厚度为0.6 mm的界面过渡层[12](见图4).

图4 多边形骨料界面层

1.4 随机骨料模型网格划分

分别对砂浆、骨料和界面3个部分进行网格划分,如图5所示.砂浆和界面采用Abaqus有限元软件中自由网格(Free)的三角单元(Tri)形式进行自动剖分,单元为四节点等参元.骨料划分网格时,在骨料内布置大尺寸种子,骨料表面布设与界面单元尺寸相同的种子,从而形成渐进的网格形式,以减少计算单元数目.砂浆单元、骨料单元和界面单元的网格控制尺寸分别为3.0,2.0,0.6 mm.

2 混凝土保护层锈胀开裂细观有限元模拟

从细观尺度出发,将混凝土看作由骨料、砂浆及骨料砂浆之间界面层组成的三相复合材料.基于已建立的二维随机多边形骨料模型,采用细观有限元模拟研究了钢筋锈蚀膨胀引起的混凝土保护层锈胀开裂行为.

(a) 砂浆

(b) 骨料

(c) 界面

2.1 细观组分材料力学参数

骨料和砂浆的材料参数通常可以直接通过试验测得,但骨料与砂浆之间的界面层材料性能则难以得到.尽管界面层的材料与砂浆材料相同,但界面层的弹性模量仅为砂浆基体的20%～50%.本文选取的混凝土细观组分材料参数见表3[12].

2.2 锈胀力的加载方法

混凝土中钢筋通常为非均匀锈蚀,锈蚀产物靠近保护层一侧较厚,远离保护层一侧较薄[13].薛圣广[14]给出了角区钢筋非均匀锈蚀层厚度的计算公式,即

表3 细观有限元模型材料参数

(4)

式中,θ为锈蚀层与x轴的夹角;u(θ)为钢筋圆周不同位置处的锈蚀层厚度;u1,u2分别为锈蚀层最大厚度和最小厚度,此处取u1=30u2;r为钢筋的半径.

本试验中将钢筋布置在混凝土角区,按照式(4)施加径向位移荷载,模拟混凝土中的钢筋锈胀荷载.钢筋直径为10 mm,将钢筋所在位置设为空圆孔,于圆孔边节点上施加径向位移荷载.所得的钢筋混凝土二维细观有限元模型如图6所示.

图6 钢筋混凝土二维细观有限元模型

3 结果与讨论

向细观有限元模型中输入不同的锈蚀层最大厚度值,以观测混凝土试件在不同锈蚀情况下应力分布.通过给定u1,根据式(4)可计算出钢筋周围不同节点处的位移值u(θ),在该位移作用下通过细观有限元模拟可以得到锈胀力,考察节点应力是否大于材料的最大抗拉应力,便可判断此时是否产生裂缝.根据文献[15],填充到界面与锈胀裂缝中的锈蚀产物并不产生锈胀力,对混凝土保护层锈胀开裂过程影响甚微,因此,利用混凝土表面开裂时钢筋的有效锈蚀率ρ来反映锈胀作用的大小,其计算公式为

(5)

式中,h为锈蚀产物膨胀率,且h∈[2.0,4.0].

当u1=1.24 μm时,右侧钢筋附近骨料与砂浆界面层应力为2.66 MPa,钢筋周围砂浆最大应力为3.86 MPa,此时界面层已经开裂并产生裂缝,而砂浆基体还处于弹性阶段,表明界面处是混凝土中的最薄弱部分,易产生混凝土内部损伤.当u1=1.25 μm时,钢筋周围砂浆开始产生裂缝.随着锈蚀的不断发展,裂缝向外扩展和延伸.当u1=9.00 μm时,混凝土表面出现裂缝,根据式(5)可计算出此时的有效锈蚀率为0.186%,表明钢筋锈蚀极易造成混凝土保护层开裂.当u1=18.00 μm时,钢筋之间的锈胀应力达到4.35 MPa,表明钢筋之间裂缝贯通(见图7(a)),此时裂缝分布与实测保护层开裂情况(见图7(b))相似,表明计算结果可靠.随着锈蚀程度的加深,保护层将会逐渐剥落.

(a) u1=18.00 μm时的平面应力云图

(b) 试件断面锈胀裂缝分布照片

4 结论

将混凝土看作由骨料、砂浆与两者之间界面组成的三相复合非均质材料,基于蒙特卡罗法在Matlab软件中编写了混凝土随机骨料生成和投放代码;利用AutoCAD软件提取随机骨料模型边界参数,导入到有限元软件Abaqus中进行网格划分;基于建立的二维多边形骨料模型,构建了钢筋混凝土二维细观有限元模型;通过在钢筋位置施加径向位移荷载,模拟了细观尺度下钢筋锈蚀导致混凝土保护层开裂的过程.结果表明,砂浆与骨料的界面处最先产生裂缝,说明界面处为混凝土中最薄弱部分,易产生混凝土内部损伤.混凝土表面开裂时钢筋有效锈蚀率仅为0.186%,说明钢筋锈蚀极易造成混凝土保护层开裂.当锈蚀层最大厚度达到18.00 μm时,混凝土中钢筋之间裂缝贯通,此时裂缝分布图与实际情况相似,说明模型计算可靠.

References)

[1]邱兆国,战宇,张凤鹏.基于塑性损伤理论的钢筋混凝土锈胀裂纹模拟[J].东北大学学报(自然科学版),2012,33(2):288-291. Qiu Zhaoguo, Zhan Yu, Zhang Fengpeng.Numerical simulation on corrosion-expansion cracks of reinforced concrete based on plastic damage theory [J].JournalofNortheastUniversity(NaturalScience), 2012, 33(2): 288-291. (in Chinese)

[2]韦俊,孟浩,薛圣广.钢筋不均匀锈蚀引起的混凝土保护层开裂有限元分析[J].西安建筑科技大学学报(自然科学版),2011,43(5):747-754. DOI:10.3969/j.issn.1006-7930.2011.05.025. Wei Jun, Meng Hao, Xue Shengguang. FEM analysis on the crack process of concrete cover induced by non-uniform corrosion of re-bar[J].JournalofXi’anUniversityofArchitecture&Technology, 2011, 43(5): 747-754. DOI:10.3969/j.issn.1006-7930.2011.05.025.(in Chinese)

[3]Chen E, Leung C K Y. Finite element modeling of concrete cover cracking due to non-uniform steel corrosion[J].EngineeringFractureMechanics, 2015, 134: 61-78. DOI:10.1016/j.engfracmech.2014.12.011.

[4]Guzmán S, Gálvez J C, Sancho J M. Modelling of corrosion-induced cover cracking in reinforced concrete by an embedded cohesive crack finite element[J].EngineeringFractureMechanics, 2012, 93: 92-107. DOI:10.1016/j.engfracmech.2012.06.010.

[5]Du X, Jin L, Zhang R. Modeling the cracking of cover concrete due to non-uniform corrosion of reinforcement[J].CorrosionScience, 2014, 89: 189-202. DOI:10.1016/j.corsci.2014.08.025.

[6]Walraven J C, Reinhardt H W. Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading[J].Heron, 1981, 26(1A): 1-68.

[7]糜凯华,武亮,吕晓波,等.三维球形随机骨料混凝土细观数值模拟[J].水电能源科学,2014,32(11):124-128. Mei Kaihua, Wu Liang, Lü Xiaobo, et al. Numerical simulation of mesostructure of concrete with 3D spherical random aggregate particles[J].WaterResourcesandPower, 2014, 32(11): 124-128. (in Chinese)

[8]高利甲,刘锡军,王玉梅.基于Matlab-混凝土二维细观结构数值模拟骨料随机投放[J].湖南工程学院学报(自然科学版),2011,21(1):81-84,94. DOI:10.3969/j.issn.1671-119X.2011.01.024. Gao Lijia, Liu Xijun, Wang Yumei. Numerical simulation for random embarking of aggregate with two-dimensional meso-structure of concrete based on Matlab[J].JournalofHunanInstituteofEngineering(NaturalScienceEdition), 2011, 21(1): 81-84, 94. DOI:10.3969/j.issn.1671-119X.2011.01.024.(in Chinese)

[9]孙立国,杜成斌,戴春霞.大体积混凝土随机骨料数值模拟[J].河海大学学报(自然科学版),2005,33(3):291-295. Sun Liguo, Du Chengbin, Dai Chunxia. Numerical simulation of random aggregate model for mass concrete [J].JournalofHohaiUniversity(NaturalScience), 2005, 33(3): 291-295. (in Chinese)

[10]高政国,刘光廷.二维混凝土随机骨料模型研究[J].清华大学学报(自然科学版),2003,43(5):710-714. Gao Zhengguo, Liu Guangting.Two-dimensional random aggregate structure for concrete [J].JournalofTsinghuaUniversity(ScienceandTechnology), 2003, 43(5): 710-714. (in Chinese)

[11]尤作磊.基于细观尺度的水泥混凝土受荷开裂模拟[D].西安:长安大学公路学院,2012.

[12]屈瑾.基于随机骨料模型的细观混凝土界面特性研究[D].杨凌:西北农林科技大学水利与建筑工程学院,2015.

[13]Yuan Y, Ji Y. Modeling corroded section configuration of steel bar in concrete structure[J].ConstructionandBuildingMaterials, 2009, 23(6): 2461-2466. DOI:10.1016/j.conbuildmat.2008.09.026.

[14]薛圣广.钢筋非均匀锈蚀引起的混凝土保护层开裂有限元分析[D].西安:西安建筑科技大学土木工程学院,2008.

[15]徐港,徐可,王青,等.钢筋混凝土结构锈胀开裂全过程仿真分析[J].建筑材料学报,2012,15(3):327-333. DOI:10.3969/j.issn.1007-9629.2012.03.007. Xu Gang, Xu Ke, Wang Qing, et al. Simulation analysis of whole cracking process due to reinforcement corrosion in concrete structures[J].JournalofBuildingMaterials, 2012, 15(3): 327-333. DOI:10.3969/j.issn.1007-9629.2012.03.007.(in Chinese)

Meso-scale finite element simulation of corrosion-induced cracking in reinforced concrete cover

Xu Yidong1Zheng Yingying2,3Du Kun3Hu Lei3

(1Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China)(2Hangzhou Traffic Investment and Construction Management Co., Ltd., Hangzhou 310015, China)(3School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

To study the influence of nonuniform characteristics of concrete on the corrosion-induced concrete cover cracking, a random aggregate model was established by using the Monte Carlo method. The codes of the aggregate generation and the delivery were compiled by the Matlab software considering the influence of the interface layer. By changing the thickness of the corrosion layer, the meso-scale finite element simulation of the corrosion-induced cracking behavior caused by corrosion of steel reinforcement was conducted.The results show that the expansion of steel reinforcement corrosion product is nonuniform. The interface layer between the mortar and the aggregate is the weakest link in the corrosion process of reinforced concrete cover. When the maximum thickness of the corrosion layer is 1.24 μm, the interface layer begins to crack and then the mortar around the steel reinforcement cracks. When the maximum thickness of the corrosion layer is 9.00 μm, the cracks appear on the surface of the concrete cover and the effective corrosion ratio of steel reinforcement is only 0.186%. When the maximum thickness of the corrosion layer reaches to 18.00 μm, the cracks between the steel reinforcement in the concrete are connected, and the crack distribution pattern is similar to that of the measured corrosion cracking, indicating that the meso-scale simulation is reliable.

steel corrosion; corrosion-induced cracking; meso-scale simulation; random aggregate model

10．3969/j．issn．1001-0505．2017．02．026

2016-09-05. 作者简介: 徐亦冬(1980—),男,博士,副教授,xyd@nit.zju.edu.cn.

“十二五”国家科技支撑计划资助项目(2015BAL02B03)、浙江省自然科学基金资助项目(LY15E080025).

徐亦冬,郑颖颖,杜坤,等.钢筋混凝土保护层锈裂行为的细观有限元模拟[J].东南大学学报(自然科学版),2017,47(2):356-361.

10.3969/j.issn.1001-0505.2017.02.026.

TU503

A

1001-0505(2017)02-0356-06