砂土直剪试验离散元数值模拟与细观变形机理研究

李 爽，刘 洋，吴可嘉

(北京科技大学 土木与资源工程学院，北京 100083)

砂土直剪试验离散元数值模拟与细观变形机理研究

李 爽，刘 洋，吴可嘉

(北京科技大学 土木与资源工程学院，北京 100083)

基于离散元法进行砂土直剪试验模拟与剪切宏细观响应研究。采用试样分条带法研究砂土剪切过程中的变形发育情况；记录应力-位移关系，分析砂土剪切应力、应变特性与剪胀特性。通过分析接触力链、接触组构分布、配位数及滑动接触百分比等细观行为演化研究颗粒细观接触状态演变；基于局部孔隙率变化分析颗粒细观分布状态演变；采用颗粒累积转动量和速度场分析颗粒细观运动状态及剪切带发育的细观机制；对离散元软件PFC2D进行二次开发，实现主应力的可视化。研究表明：应变局部化集中于颗粒转动、接触滑动、体胀明显的剪切带内，剪切带内外颗粒不同的运动状态导致细观参量的变化，剪切带厚度为(10～15)d50；力链网络、接触组构和主应力场本质上是一致的，三者主方向在剪切过程中发生了近似一致的偏转。

砂土；离散元法；直剪试验；细观力学；剪切带

1 研究背景

土作为离散颗粒聚集体，具有离散性、非各向同性、细观随机性等特殊性质，造成其剪切机制的复杂性。直剪试验是一种简单有效的土强度室内试验测定方法[1]，广泛应用于测定散粒介质的抗剪强度和流动性质。土体试样在直剪时受剪切作用会发生变形，伴随颗粒的转动、滑移、破碎，当变形逐渐发育并集中于某一区域内时，试样发生失稳并破坏，通常将此局部变形区域称为剪切带。剪切带的形成和演变导致土体的失稳和破坏，是决定土体强度的薄弱区域[2-3]。

目前剪切带理论的研究成果主要有：局部分叉理论、梯度塑性理论、非局部理论、Cosserat理论及复合体理论等。常规直剪仪虽能得到抗剪强度指标，但不能分析试样在剪切过程中的应力-应变关系和微细观力学响应，对剪切带的研究也受到限制。基于此，刘文白等[4]开发了半膜式细观结构观测直剪仪，研究了砂土试样在剪切过程中的应力应变场演变，但研究中未从颗粒运动角度对相关微细观力学行为进行分析。由于物理试验对于微细观力学研究来说限制较多，且耗时费力，数值试验手段可作为其有效补充。其中，Potts等[5]、Tejchman等[6]分别采用基于弹塑性模型和亚塑性模型的有限元法研究了砂土直剪力学性质及剪切带的应变局部化演变，并分析了边界效应和颗粒直径对剪切带厚度的影响。但由于有限单元法无法针对微细观(颗粒)层面剪切应力与变形演变的机理进行探究，而离散元法在土体细观机理研究方面体现出独特的优势。Thornton等[7]基于离散元法对散粒体直剪试验进行了模拟，Liu等[8]基于离散元法研究了粒状体的直剪力学特性，Masson等[9]基于离散元法对松密试样的剪切力学响应进行了宏细观分析与对比研究，Wang等[10]采用离散元法对散粒体直剪试验的尺寸效应进行了探究，蒋明镜等[11]通过离散元法研究了单粒组密砂剪切带的形成过程。因此，离散元法作为土微细观力学研究的有效手段，是对物理试验研究的有益补充，离散元数值试验有重要的研究与指导意义。

本文利用二维颗粒流程序对砂样直剪试验进行数值模拟，并进行细观组构统计开发和主应力可视化开发，选定特征状态对砂样直剪过程中的受力及变形宏细特性进行全面分析，揭示砂土剪切的本质机理。着重研究以下问题：①砂样直剪中的变形发育情况及剪切带形成过程；②从颗粒接触状态、颗粒分布状态和颗粒运动状态3方面分析直剪过程中砂样的细观力学特性演变；③主应力可视化开发与直剪过程中砂样的主应力矢量分布演变研究。

2 直剪试验离散元分析过程

砂土离散元试样的尺寸为70 mm×30 mm，试样的粒径范围为0.5～0.7 mm均匀分布，平均粒径d50为0.6 mm。试样初始孔隙率0.175，颗粒总数6 127个。离散元模型采用6道刚性墙体边界模拟直剪试验的剪切盒，并生成2道水平刚性墙体防止剪切过程中的颗粒溢出。

粒间接触模型采用接触刚度模型，符合无黏性土的特性。试样主要的细观参数包括颗粒间及颗粒与墙体间法向接触刚度、切向接触刚度、摩擦系数，取值列于表1中。其中，颗粒间的接触刚度是决定散粒试样弹性模量的重要参数，根据散粒体弹性理论，当颗粒接触刚度的取值在108～109N/m之间，法向和切向刚度比值在1～3之间时，模型收敛性良好[12]。本次数值试验设定颗粒间及颗粒与墙体间的法向接触刚度、切向接触刚度分别为1.5×108，1.0×108N/m,二者比值为1.5，颗粒间摩擦系数设为0.5，颗粒与墙体间的摩擦系数设为0。

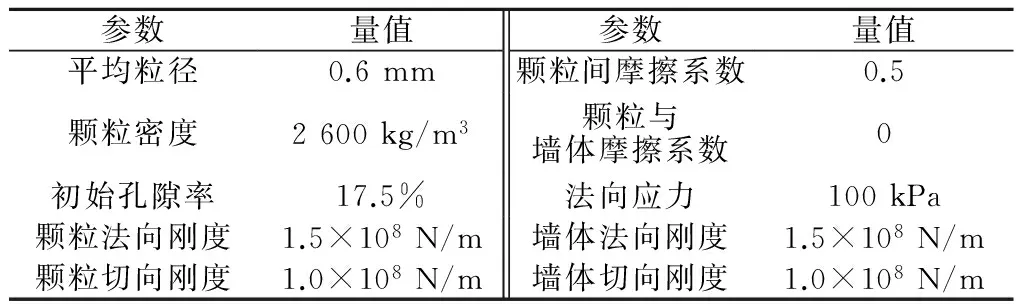
表1 离散元模型参数Table 1 Parameters of discrete element model

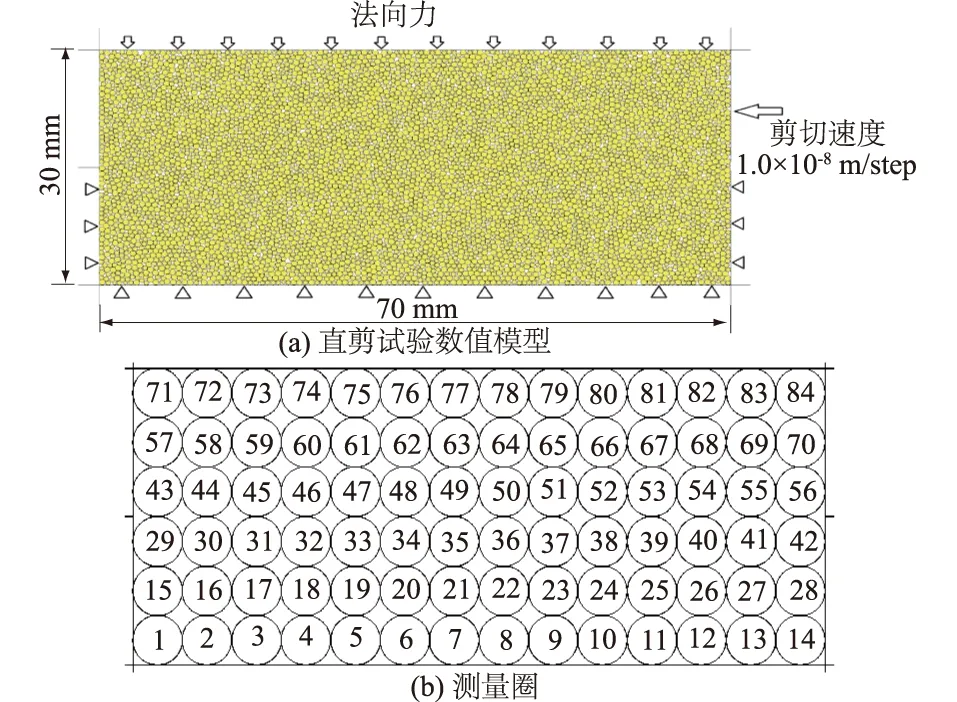
图1 直剪试验数值模型及测量圈Fig.1 Model of direct shear simulation test and measurement circles

试样生成后，通过伺服程序施加100 kPa 法向力，使试样固结稳定。随后固定下盒，保持法向应力为100 kPa的常应力条件，并给上盒施加一个向左的速度实现上下盒的相对运动，以模拟砂土直剪试验。数值试验的示意图如图1(a)所示。

为了监测试样内局部孔隙率、配位数、滑动接触百分比等细观参量的变化，并实现主应力偏转可视化二次开发，在试验前建立了如图1(b)所示的监测测量圈。

3 宏观力学特性分析

3.1 宏观应力-应变特性

土工直剪仪上下盒各自的侧面边界并不能发生相对运动，故直剪试验过程中试样的体积只能沿竖直方向发生膨胀或收缩，试验时可记录试样的高度变化反映其剪胀性。同时设置监测记录剪切过程中的剪切应力、剪切位移，得到砂土试样剪切5 mm过程中的剪切应力、剪切位移、体积变化三者之间的特征曲线如图2所示。

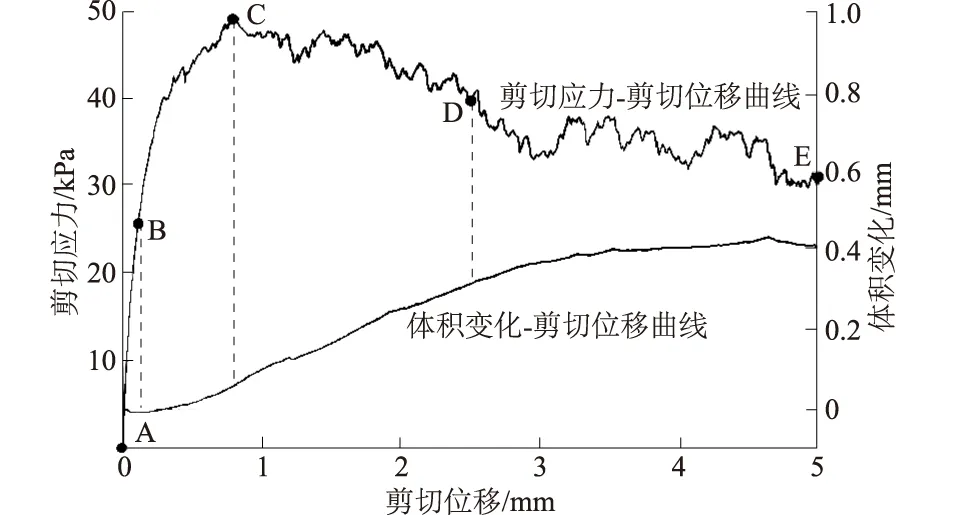
图2 剪切应力-剪切位移及体积变化-剪切位移曲线Fig.2 Curves of shear stress vs. shear displacement and volume change vs. shear displacement

由图2中的剪切应力-剪切位移曲线可知，试样符合应变软化型特征，达到峰值应力状态后会发生应变软化现象，最终发育到残余状态。试样的峰值强度约为49 kPa，峰值应力比为0.49；残余强度约为31 kPa，残余应力比为0.31。根据剪切应力-剪切位移、体积变化确定图中A，B，C，D，E 5个状态作为特征状态以研究试样在剪切过程中的宏细观力学行为演变。这5个状态对应的剪切位移、体变情况、剪切应力及描述列于表2中。

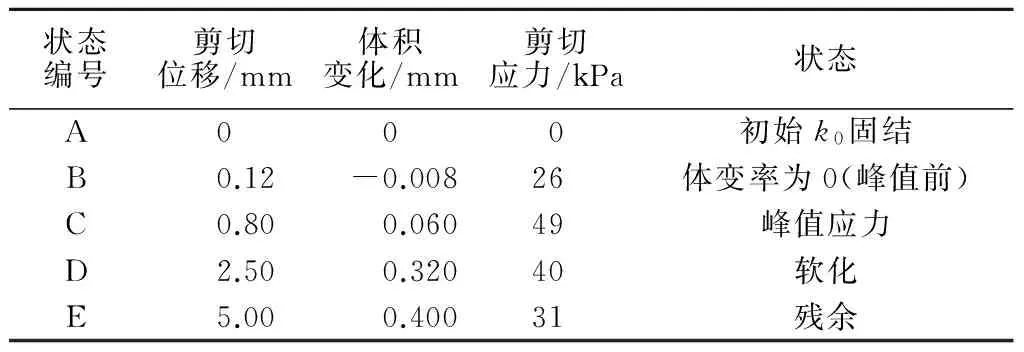
表2 特征状态Table 2 Characteristic states

根据体变曲线可知，砂土试样在剪切过程中先发生体积收缩后发生体积膨胀，剪切完成后整体表现出剪胀性，剪切位移为5 mm时的试样沿竖向膨胀0.4 mm。进入残余状态时，试样体积基本不发生变化。结合剪切应力-剪切位移特征曲线可知，该砂土试样表现出密砂的性状。

3.2 剪切中的变形演变

土体力学特性研究中，非连续、局部化发育的变形是重点研究问题。为了研究剪切过程中试样内各个位置的变形演变情况，在本次直剪试验模拟前，于试样中设置了9个黑色纵列，监测直剪过程中纵列的变形演变过程如图3。

图3 试样变形演变Fig.3 Evolution of specimen’s deformation

由图3(c)可以看出，剪切开始时，试样内统一纯剪切是变形的主导模式， 纵列基本不发生变形，颗粒的位移连续且均匀，处于纯剪切状态。达到峰值应力状态时，仅靠近侧边界的纵列1和纵列9发生了轻微的变形。峰值应力状态后，非线性的应力应变状态成为主导，随着剪切位移的增大，纵列变形由外向内逐渐发育，应变局部化现象越来越明显。剪切完成后，变形集中于一个条带状区域内，即为应变局部化的剪切带区域。剪切带边界区域变形最大，向内逐渐减小。因此，试样在峰值前以纯剪切变形模式为主导，总体变形很小；峰值后以非线性应力应变为主导，由剪切面两侧向内逐渐发育变形，最终形成应变局部化条带区。

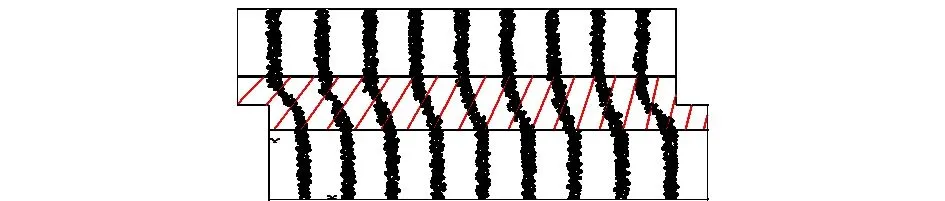
图4 试样剪切变形情况Fig.4 Shear deformation of specimen

图4所示的是剪切后纵列的变形情况，可以看出，图示阴影条带区域内的纵列发生了相对更为明显的弯曲变形。可认为该变形局部化条带区域即为剪切带，其厚度近似为(13～15)d50。

4 细观力学特性分析

4.1 颗粒接触状态分析

4.1.1 力链网络

力链网络是土骨架体系上粒间接触力的宏观形式，可体现颗粒体系受外荷载作用时受力响应机制的敏感性。图5所示的是试样在不同剪切阶段的力链网络演变。试样在法向力作用下固结稳定后，强力链基本沿竖直方向均匀分布。剪切开始后，峰值应力状态前，在右上侧墙体施加的剪切力作用下，力链网络的分布开始发生变化，变化的区域集中于右上角和左下角区域，试样中部的力链基本还是沿着竖直方向。达到峰值应力状态时，力链网络的均匀性和分布特征完全改变，力链集中形成几条强力链，强力链在左下角和右上角沿着水平方向，在试样中部沿着倾斜30°～45°的方向。到达峰值应力状态后，随着剪切位移的增大，力链网络进一步演化，强力链更为集中，剪切5 mm后的倾角也近似为30°～45°。

图5 接触力链网络演变Fig.5 Contact force chains in specimen

4.1.2 组构分布

土的接触组构指标[13]是反映其微细观各向异性发展的重要指标，其可有效量化土体微细观特性对宏观力学响应的影响，以建立宏观力学与细观响应的内在联系。接触组构中接触法向组构(E(θ))、法向接触力组构(fn(θ))和切向接触力组构(ft(θ))可采用Rothenburg等[14]建议的傅里叶函数分别表示为：

(1)

式中：θ是颗粒间接触法向的角度；f0是所有颗粒间法向接触力平均值；θa，θn，θt分别是颗粒间接触法向、法向接触力和切向接触力各向异性分布主方向的角度；a，an，at是傅里叶拟合系数，分别反映颗粒间接触法向、法向接触力和切向接触力分布的各向异性程度。

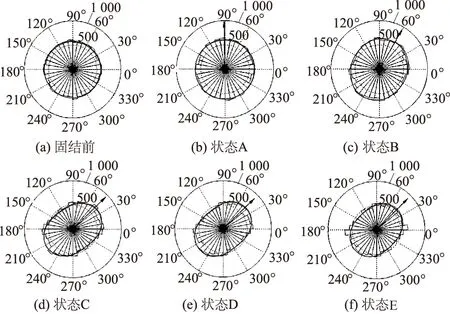
图6 接触法向分布Fig.6 Normal direction distribution of contact

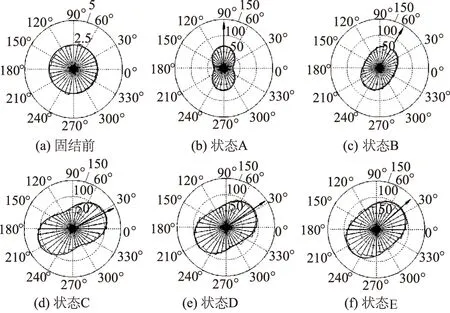
图7 法向接触力分布Fig.7 Distribution of normal contact force

本次数值试验得到剪切过程中试样的接触法向分布、法向接触力和切向接触力分布见图6至图8所示。其中：图6中的数字为接触数目；图7、图8中的

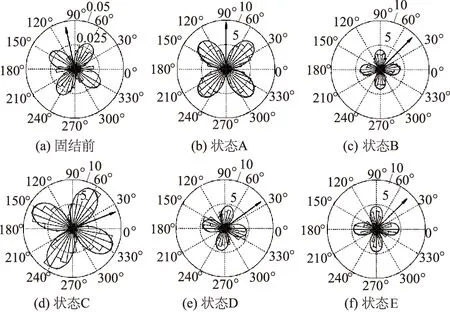
图8 切向接触力分布Fig.8 Distribution of tangential contact force

数字均为接触力(N);接触法向指标为接触切面法线在对应方向上的接触数目；法向接触力和切向力为对应接触法向上法向接触力和切向力的平均值；粗实线即为式(1)中傅里叶分布函数的拟合曲线。可发现剪切前试样内粒间接触法向分布较为均匀，而剪切破坏了试样接触法向分布的均匀性。随着剪切位移增加，0°～60°内的接触数逐渐增多，而120°～180°内的后粒间的接触数逐渐减少。达到峰值应力状态时，接触法向分布的形状由圆形变为椭圆形，主轴偏转至45°左右。峰值后的软化阶段与残余阶段，接触法向的主轴方向基本不发生变化，形状只有微小的改变。

接触力可分解为法向和切向接触力。剪切过程中切向接触力比法向接触力小一个量级，二者矢量叠加所得接触力的大小和方向实际与法向接触力非常相近。因此，理论上可认为法向接触力分布的演变与力链网络的演变本质上是非常相近的。由模拟结果可知，剪切过程中法向接触力分布近似呈“花生状”或椭圆形，主轴方向的演变近似为：90°→60°→25°→35°→40°，与力链网络的演变情况基本一致，也可发现法向接触力在达到峰值前逐渐增大的现象。切向接触力分布呈对称的“花瓣状”，在剪切过程中也发生了大小变化与类似的主轴偏转现象。

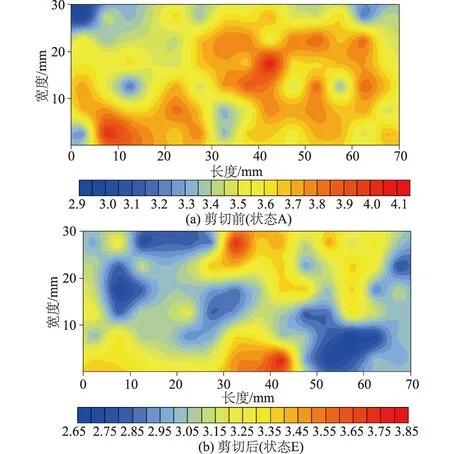
图9 配位数分布演变Fig.9 Evolution of coordinate number distribution

4.1.3 配位数

配位数指颗粒的平均接触数，配位数越大，颗粒间的受力传递越充分[15]。砂土剪胀性本质上是由砂土颗粒在荷载作用下发生重排列而导致的，颗粒的滑移、转动和重组必然会导致试样内配位数的变化。剪切前后的配位数分布如图9所示。

若将试样分成如图10所示的6个宽度相等、距盒底高度不同的条带，由下到上分别编号为Z1，Z2， Z3，Z4，Z5，Z6，可得到剪切过程中各个条带区域内的平均配位数变化情况。

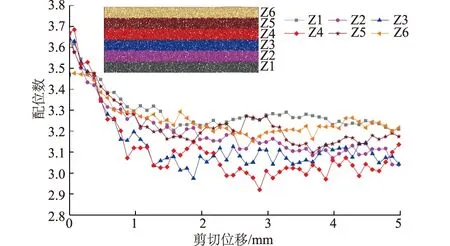
图10 6个条带的配位数变化曲线Fig.10 Curves of coordination number in six zones

由图9可以看出，剪切作用下试样内配位数的大小及分布发生变化，剪切后试样内多数区域内配位数都有所降低。由图10可以看出，各条带内的配位数在剪切开始后随剪切位移的增大而逐渐减小，当剪切位移达到1.5 mm后基本保持不变，稳定在3.0～3.3之间。同时也可看出，剪切带内配位数相对于带外降低更显著。

4.1.4 滑动接触百分比

滑动接触百分比是颗粒间发生滑动的接触数占总接触数的比例。剪切前后的滑动接触百分比分布如图11。

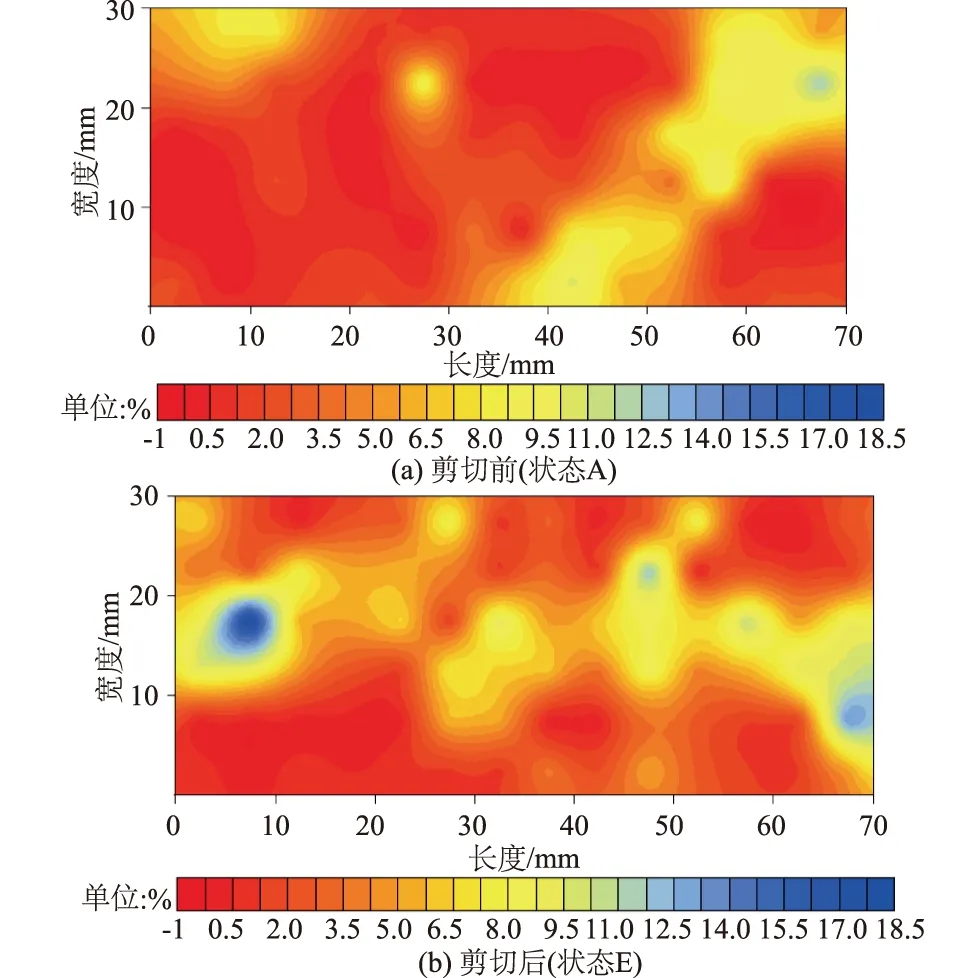
图11 滑动接触百分比分布Fig.11 Evolution of sliding contact distribution

图11中出现了滑动接触百分比为-1%的情况，这是由于云图网格计算方法导致的，实际并不会出现此种情况。对比剪切前后的滑动接触百分比分布图可知，剪切完成后剪切面附近区域接触滑动比例明显增大，意味着剪切作用下剪切面附近区域内颗粒间的接触发生了相对更为剧烈的滑动，可认为此条带即为剪切带。

4.2 局部孔隙率演化分析

剪切过程中试样孔隙率分布的变化情况如图12所示。从图12中可以看出，剪切开始后，试样由剪切面两端附近的局部区域开始发生孔隙率增大现象，并随着剪切位移的增大逐渐向内发育直至贯通。最终，试样在剪切面附近形成了明显的孔隙率增大的条带区域，可认为其即为剪切带，孔隙率增大的现象本质上是由密砂的剪胀性导致的。由图12(c)得到剪切带厚度近似为(10～15)d50。

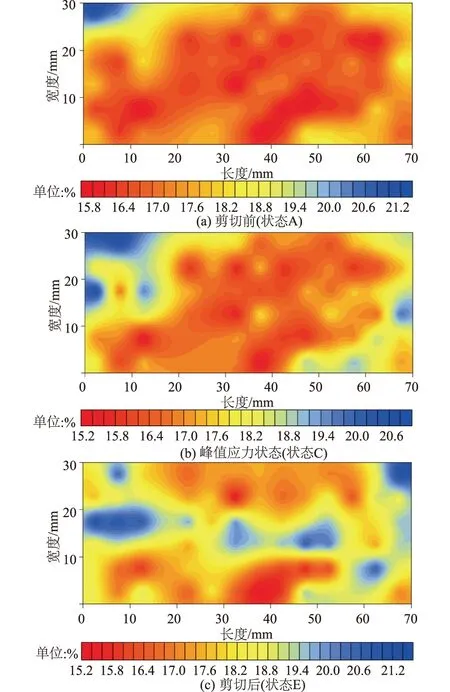
图12 孔隙率分布Fig.12 Distribution of porosity

按与图10一致的形式进行分区，得到剪切过程中各个条带内的孔隙率演化情况如图13所示。可以看出，剪切面附近的条带Z3和Z4发生了明显的孔隙率增大现象，其他条带内的孔隙率变化量相对较小，验证了上述的孔隙演变分析。因此，密砂在剪切过程中，剪切面附近区域由外向内逐渐发育孔隙率增大区域，贯通形成剪切带，剪切带内发生剪胀，导致试样整体的剪胀；带剪切带外发生轻微剪胀或剪缩，对试样的剪胀性质影响不大。

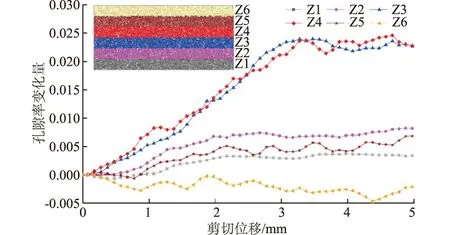
图13 6个条带内的孔隙率变化Fig.13 Porosity changes in six zones

4.3 颗粒运动状态分析

4.3.1 颗粒速度场

砂样在B和C这2个特征状态的瞬时速度场如图14所示。由峰值前B状态的速度场可以看出，刚开始剪切时，试样除了4个角的区域外，整体速度较均匀，符合峰值前统一纯剪变形模式。达到图14(b)所示的峰值应力状态时，试样内速度出现上盒大下盒小的现象，剪切面附近尤其是两端的颗粒大多都有竖向速度分量，此时颗粒发生上下错动，会促进剪胀现象的发生。认为剪切面附近的剪切带为速度过渡区域，不仅发生速度大小的过渡，方向也发生变化。试样在剪切面左侧边界和右侧边界局部区域内出现了速度涡旋现象。

图14 速度场Fig.14 Velocity fields

4.3.2 颗粒累计转动量

基于颗粒流程序的累计转动量函数统计颗粒的累计转动量，以特定转动量(本数值试验设为15°)为界限，将转动量大于特定值和不大于特定值的颗粒分别设定为黄色和红色。得到剪切过程中的颗粒累计转动情况如图15。可发现，峰值前试样内颗粒累计转动量很小，达到峰值应力状态时，在剪切面两侧的边界形成了剧烈转动区域。峰值应力状态后，随着剪切位移的增大，剧烈变形区域由两侧逐渐向内部发育，贯通后形成初始的带状区域，进一步发育，条带的厚度逐渐增大。

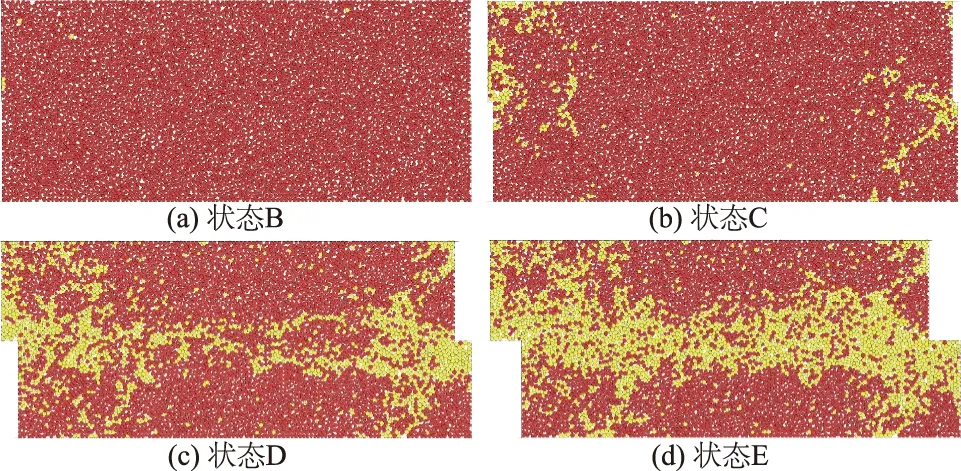
图15 颗粒累计转动量演变Fig.15 Evolution of particle’s cumulative rotation

结合变形和孔隙演变可知，刚开始剪切时，剪切带并未形成，随着剪切位移的增大，变形不断增大，颗粒转动不断加剧，变形、转动和膨胀由剪切面两侧的局部区域逐渐向内发育贯通，最终形成了变形、颗粒转动和体胀集中的剪切带区域。

4.4 主应力场分析

基于二向应力状态解析法计算各测量圈内的主应力和主方向，并以测量圈的圆心为基点计算主应力矢量的端点，建立表示2个主应力相对大小和分布方向的可视化墙单元，以实现主应力的可视化。得到砂样在直剪过程中主应力分布如图16所示。

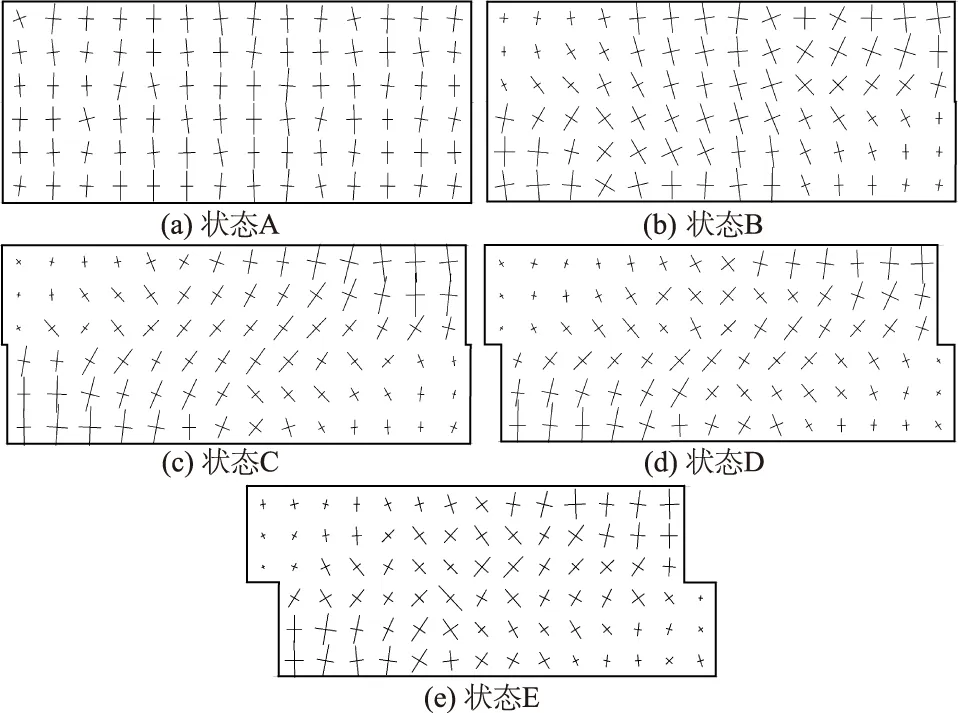
图16 主应力场分布Fig.16 Distribution of principal stress field

剪切前试样的初始应力场分布较为均匀，主应力分布反映的试样内部受力状态与力链网络一致。随着剪切位移的增大，主应力场开始出现明显的偏转并且变得不均匀，左上角和右下角的主应力相对减小。峰值应力状态时，主应力的偏转最明显且统一。结合力链网络及接触组构分布变化可知，峰值应力状态时，接触组构的主轴方向及强力链的方向与主应力偏转后的方向基本一致，此时砂样的剪切抗力能得到最大发挥。这表明，主应力场、接触组构分布和力链网络反映的细观受力机制在本质上是一致的，剪切中三者发生了近似一致的主方向偏转。

5 结 论

(1) 直剪过程中砂样的应力、应变分布都存在不均匀性。剪切过程中，试样变形集中于剪切带内；主应力和力链分布区域化且发生了主方向的偏转。强力链、接触组构主轴及主应力方向发生了一致的偏转，三者本质上具有一致性，反映了颗粒体系在外荷载作用下的内部响应。

(2) 受剪切力和法向力综合作用，试样由剪切面两端开始发育局部变形，颗粒发生剧烈转动及上下错动，导致孔隙率的增大和接触的滑动，随着剪切位移增大逐渐向内贯通形成剪切带。带内外颗粒处于不同的运动状态，导致了变形局部化区域的发育，剪切带的厚度近似为(10～15)d50。

(3) 直剪试验条件下剪切带内外颗粒处于不同的运动状态，带内颗粒发生转动和上下错移，带外颗粒发生平动，导致试样组构、孔隙率、配位数、滑动接触百分比等细观参量分布的变化，这些细观参量的变化也反映了剪切带宏观应变局部化现象与剪胀现象。

[1] 史旦达, 周 健, 刘文白, 等. 砂土直剪力学性状的非圆粒模拟与宏细观机理研究[J]. 岩土工程学报, 2010, 32(10): 1557-1565.

[2] 蔡正银, 李相崧. 无黏性土中剪切带的形成过程[J]. 岩土工程学报, 2003, 25(2) : 129-134.

[3] 张 兆, 刘元雪. 应变局部化理论及在岩土工程中的应用[J]. 后勤工程学院学报, 2004, (2):12-15.

[4] 刘文白, 张 辉, 邓一兵. 基于DPDM技术的砂土直剪试验剪切过程中的应力场分析[J]. 中国水运, 2008, 8(7): 235-239.

[5] POTTS D M, DOUNIAS G T, VAUGHAN P R. Finite Element Analysis of the Direct Shear Box Test[J]. Geotechnique, 1987, 37(1): 11-23.

[6]TEJCHMAN J, BAUER E. FE-simulation of a Direct Shear and a True Simple Shear Test within a Polar Hypoplasticity[J]. Computers and Geotechnics, 2005, 32(1):1-16.

[7] THORNTON C, ZHANG L. Numerical Simulation of the Direct Shear Test[J]. Chemical Engineering and Technology, 2003, 26(2): 153-156.

[8] LIU S H, SUN D A, MATSUOKA H. On the Interface Friction in Direct Shear Test[J]. Computers and Geotechnics, 2005, 32(5):317-325.

[9] MASSON S, MARTINEZ J. Micromechanical Analysis of the Shear Behavior of a Granular Material[J]. Journal of Engineering Mechanics, 2001, 127(10): 1007-1016.

[10]WANG J, GUTIERREZ M. Discrete Element Simulation of Direct Shear Specimen Scale Effects[J]. Geotechnique, 2010, 60(5): 359-409.

[11]蒋明镜, 王富周, 朱合华. 单粒组密砂剪切带的直剪试验离散元数值分析[J]. 岩土力学, 2010, 31(1): 253-257.

[12]MISHRA B K, MEHROTRA S P. Modeling of Particle Stratification in Jigs by the Discrete Element Method[J]. Minerals Engineering, 1998, 11(6): 511-522.

[13]ODA M. Initial Fabrics and Their Relations to Mechanical Properties of Granular Material[J]. Soils and Foundations, 1972, 12(1):17-36.

[14]ROTHENBRUG L, BATHURST J. Analytical Study of Induced Anisotropy in Idealized Granular Materials[J]. Geotechnique, 1989, 39(4):601-614.

[15]刘 洋, 吴顺川, 周 健. 单调荷载下砂土变形过程数值模拟及细观机制研究[J]. 岩土力学, 2008, 29(12): 3199-3204.

(编辑：姜小兰)

Exploring Mesoscopic Deformation Mechanism of Sand in Direct ShearTest by Numerical Simulation Using Discrete Element Method

LI Shuang, LIU Yang, WU Ke-jia

(School of Civil and Resource Engineering, University of Science and Technology Beijing,Beijing 100083, China)

Direct shear test of sand was simulated using discrete element method and the macro-and-mesoscopic responses of sand during shearing were analyzed in this research. The development of sand deformation was observed through strip partition method; and the relationship between shear stress and shear displacement was recorded to analyze the macroscopic behaviors of sand. In mesoscopic scale, the development of contact status was researched through analyzing contact force chain, contact fabric distribution, coordination number and sliding contact percentage; the evolution of granular distribution under shearing was observed through the analysis of porosity variation;the granular motion state and the mesoscopic formation mechanism of shear band were studied through observing the cumulative rotation and velocity of particles. Furthermore, principal stresses and their inclinations in specimen were visualized through secondary development of PFC2D. The study shows that strain is concentrated in the shear band in which particle rotation, contact sliding and obvious dilatancy are observed. Different motion state of particles inside and outside the shear band leads to the changes of mesoscopic parameters, and the thickness of shear band is 10-15 times ofd50. Contact force chain network, contact fabric distribution and principal stress distribution are essentially consistent, and the principal direction changes consistently during shearing.

sand; discrete element method; direct shear test; meso-mechanics; shear band

2015-11-27；

2015-12-21

国家自然科学基金项目(51178044)；北京高校青年英才计划资助项目(YETP0340)

李 爽(1993-)，男，安徽滁州人，硕士研究生，主要从事散粒体细观力学研究与数值模拟，(电话)15201451398(电子信箱)ls19931014@126.com。

10.11988/ckyyb.20151006

2017,34(4):104-110,116

TU43

A

1001-5485(2017)04-0104-07