基于Matlab-GUI的数值积分界面设计
张建斌, 赵 静, 许晓晴
(长安大学 经济与管理学院, 西安 710064)
基于Matlab-GUI的数值积分界面设计
张建斌, 赵 静, 许晓晴
(长安大学 经济与管理学院, 西安 710064)

为了解决原函数完全未知、原函数已知但其形式复杂、原函数已知且存在解析解3种情况下的复杂积分计算问题,提出了关于数值积分界面的设计。将Matlab中可开发的GUI工具结合数值积分计算中的典型算法构造开放式的用户界面,设计出数值积分求解器并实现数值积分可视化功能;同时通过采用自定义方式设置积分区间等分数的思路,提高了梯形、辛普森、复合梯形、高斯-勒让德数和自适应5种积分方法的计算精度。最后,用所设计的数值积分GUI界面对3种类型复杂积分函数进行验证和求解,结果表明,该设计能在同一界面同时实现用5种积分方法按用户任意设定的精度进行积分求解并能将计算结果可视化,因此该界面具有适应性强、使用方便、界面友好、操作简洁的优点。
数值积分; 图形用户界面; Matlab; 积分求解器; 可视化
0 引 言
Matlab是一个基于矩阵运算,有强大的数据处理能力的工具箱。它既能进行科学计算,又能开发出所需的图形界面。Matlab-GUI是指图形用户界面,用户可以根据自己的需要,通过构思和编辑GUI,创建方便快捷的窗口,执行一些如计算、绘图和仿真等可视化操作。在当今科学研究和工程实践过程中,模型建立结果通常涉及诸如e-x^2等复杂函数的积分问题,其原函数不能用初等函数表达,从而积分基本定理牛顿-莱布尼茨(Newton-Leibniz)公式[1]
则不能求解出其积分值。而数值积分理论提供了多种求解被积函数近似积分值的方法,因此,在实际生活中数值计算已经发展成为一个重要的研究方法。
Matlab-GUI设计模块受到了许多研究者的青睐,在各个领域中都有它的应用。利用Matlab-GUI与其他学科的融合,大大方便了研究者的深入学习和 研究。鲁晓东[2]利用Visual C++与Matlab-GUI混合编程,提高了软件交互界面的友好性;张鸣[3]把Matlab-GUI融入到通信原理的课程中,丰富了实验教学手段;李彤等[4]把Matlab-GUI应用到了材料力学中,对力学教学提供了方便的演示手段;钟可君等[5]采用Matlab-CUI对光学实验进行仿真,为光学理论分析提供了方便;谢丽蓉[6]更是采用Matlab-GUI开发出了研究异步电机特性的虚拟平台。兰红等在应用Matlab-GUI进行图像处理、飞机下滑控制、车辆路径及过程控制等问题的建模与仿真方面进行了相关研究[7-10]。在数学方面,有关GUI可视化功能在求解线性方程组和高等数学教学实验及图形用户界面系统开发方面的应用[11-14],而数值积分研究理论知识与Matlab-GUI设计相结合的讨论则相对较少。其中2009年于育民[15]在Matlab-GUI数值积分中的应用一文中写过相关内容,但是他没有充分利用Matlab-GUI设计所涉及到的一些细节问题,诸如:没有个性化的数值积分界面设计;没有导入音乐功能,不能为用户提供轻松快乐的操作环境;没有设计菜单板块,不能实现积分结果的输出和积分界面退出功能;忽略了GUI中指针功能,没能实现在有限积分界面中为用户传递更多信息,操作更加便捷的功能;没有将各种积分方法结果同时呈现于同一界面,使用户无法比较不同方法积分结果的差异程度。本文将集成Matlab系统的ODE suite及自定义的常见数值积分方法,设计一个数值积分求解器。为用户提供一个简单、便捷的可视化操作界面。
1 Matlab-GUI积分界面功能
将Matlab-GUI应用于设计积分界面,为没有深入学习过数值积分理论知识和不了解Matlab-GUI相关知识的人提供了极大的方便,实现可视化果。主要功能如下:
(1) 个性化的数值积分界面,能够吸引用户的眼球。
(2) 该界面能够同时求解被积函数在5种数值积分方法下任意精度的积分结果,并能同时比较不同积分方法求解结果的准确程度。
(3) 该界面能够绘制出被积函数在自变量取值范围内的函数图,并在图中标注出积分区间部分。
(4) 该界面能绘出被积函数在积分区间上的函数图,并进行左矩形积分动画演示,让用户对数值积分的几何意义有直观、形象的理解。
(5) 该界面利用指针功能实现多个GUI界面相结合的方法,不但节省了积分界面空间,而且使界面设计更具有人性化和条理化。
(6) 该界面利用指针导入音乐,并且可以实现随时播放和停止的功能,为用户操作提供了轻松愉快的环境。
2 Matlab-GUI界面设计
GUI界面的制作包括前台界面设计和后台程序编写两部分,其制作过程需要进行反复修改,才能实现相应的功能。它的一般制作过程如图1所示。

图1 GUI制作流程图
2.1 主界面设计
设计的主要目的是实现Matlab-GUI与数值积分的结合,得到相应的积分界面。为了使设计的GUI更加人性化,让用户对该设计的目的有更清晰的了解。专门设计了个性化的主界面,其设计思路为:像其他开发软件拥有自己个性的主界面一样,将设计标题嵌入主界面,当运行该程序时,伴随着10 s的优美音乐。另外设置了Start按钮,单击它时可跳过音乐直接进入积分界面。实现上述功能的核心控件代码如下:
II=imread(‘启动页面.bmp’);
image(II)
colormap gray
set(ha,‘handlevisibility’,‘off’,‘visible’,‘off’);
global p %音乐播放
[y,fs,bits]=wavread(‘启动音乐.wav’);
p=audioplayer(y,fs);
play(p)
设计的GUI主界面如图2所示。
图2 GUI主界面
2.2 界面菜单项设计
Matlab-GUI中菜单项设计包括下拉式菜单编辑和现场菜单编辑两部分。本文在文件主菜单下设计了两个子菜单项,分别为积分和关闭。用户可以通过积分界面菜单项实现相应的功能。以积分菜单项的设计为例,其设计过程如下,首先在两种菜单编辑下编辑文件主菜单,并正确调用其相应函数。然后将子菜单项积分的Tag设置为“jifen”,用于求得函数的积分,设置其调用函数为:
Function jifen_Callback(hObject, eventdata, handles)
pushbutton3_Callback(hObject, eventdata, handles);
设计界面过程如图3所示。
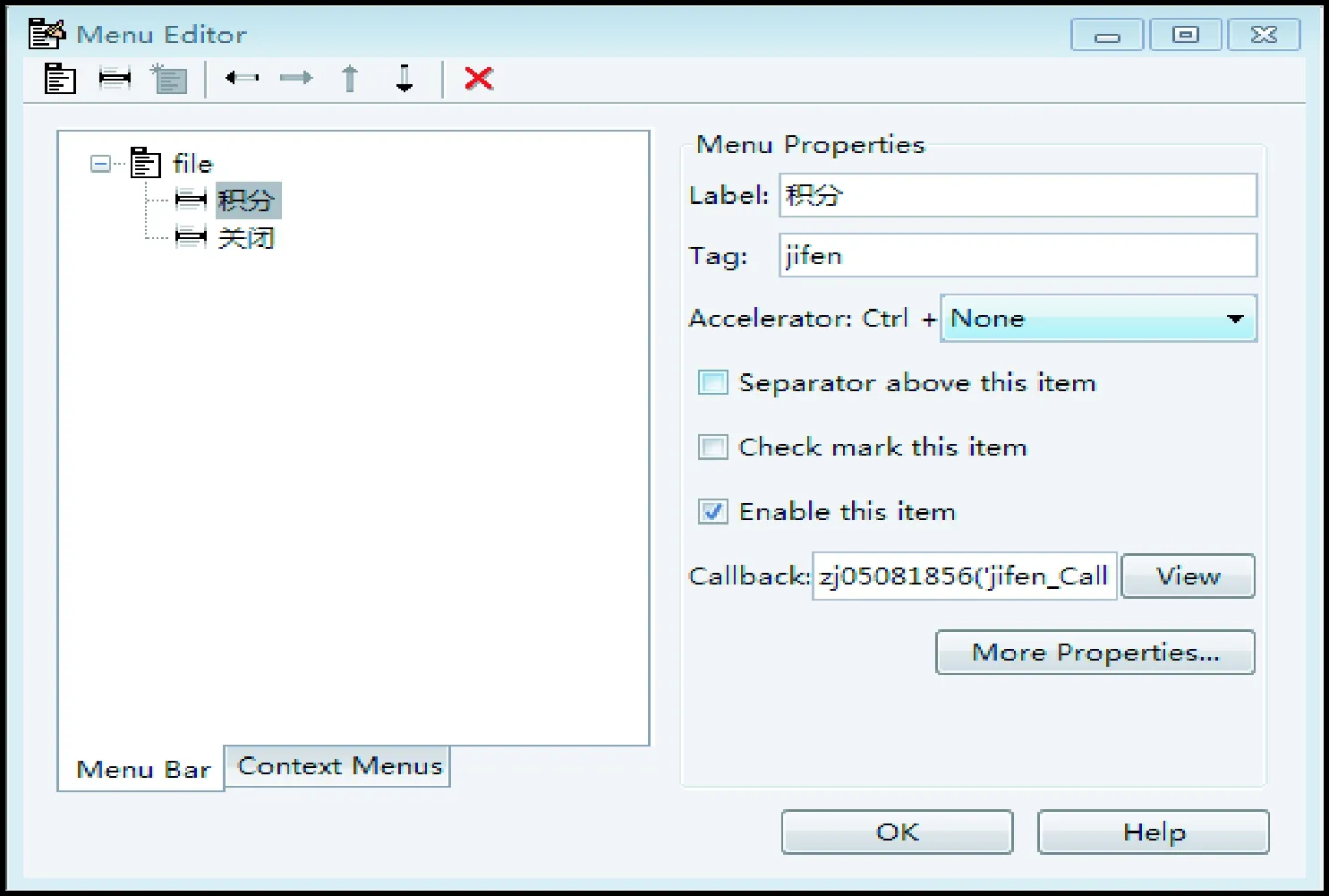
图3 GUI菜单项设计图
2.3 积分界面设计
积分界面的主要功能为实现求解一元函数分别在梯形法、Simposon、复合梯形、高斯-勒让德和自适应数值积分方法下的积分值,其中精度设计由等分数n来确定。其中涉及到的求解过程均是根据理论编写相应代码,而不是Matlab自带的求解命令。设计左矩形动画演示程序,使用户清楚理解积分的几何意义。编辑绘图区域,方便用户得到被积函数在积分区间下的函数图。同时,利用GUI与GUI之间的调用功能,设计说明和注意事项按钮,为用户提供了方便使用说明及如何应对使用过程中可能出现的问题。最后设计背景音乐区域,该区域设计了音乐下拉菜单,用户可以选择喜欢的音乐,并能够实现随时播放和停止的功能。其GUI控件布局结构如图4所示。
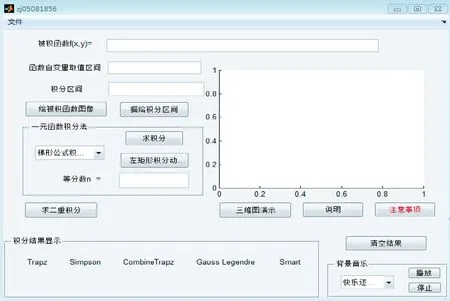
图4 GUI积分界面
积分方法选择及其相应积分结果控件实现的核心代码实现过程为:首先通过输入一元函数或二元函数,并给出自变量的取值范围记为a,b,将函数表达式及相应参数值传递给积分方法选择控件,该控件为下拉菜单,通过选择积分方法,并调用与该方法对应的程序,最后将运行结果显示在积分结果区域。
其中获得函数及积分区间的代码为:
a=str2num(get(handles.kj3,‘string’));
b1=a(1); b2=a(2); d=0.001;
x=b1:d:b2;
c=get(handles.kj1,‘string’);
f=inline(c,‘x’);
积分方法选择中主要使用了switch语句,其中的核心代码为:
switch var
case 1
m=trapr1(f,b1,b2,n);
⋮
case 4
m = Gauss_Legendre(f,b1,b2,10)
⋮
case 5
m=SmartSimpson(ff,b1,b2);
⋮
end
音乐功能区域实现包括播放和停止两个部分,其相应的回调函数分别为:
音乐播放按钮的回调函数:
function pushbutton7_Callback(hObject, eventdata, handles)
global p
[y,fs,bits]=wavread(‘背景音乐.wav’);
p=audioplayer(y,fs);
play(p);
音乐停止按钮的回调函数:
function pushbutton8_Callback(hObject, eventdata, handles)
global p
pause(p);
其中GUI与GUI的调用说明部分设计如图5所示。
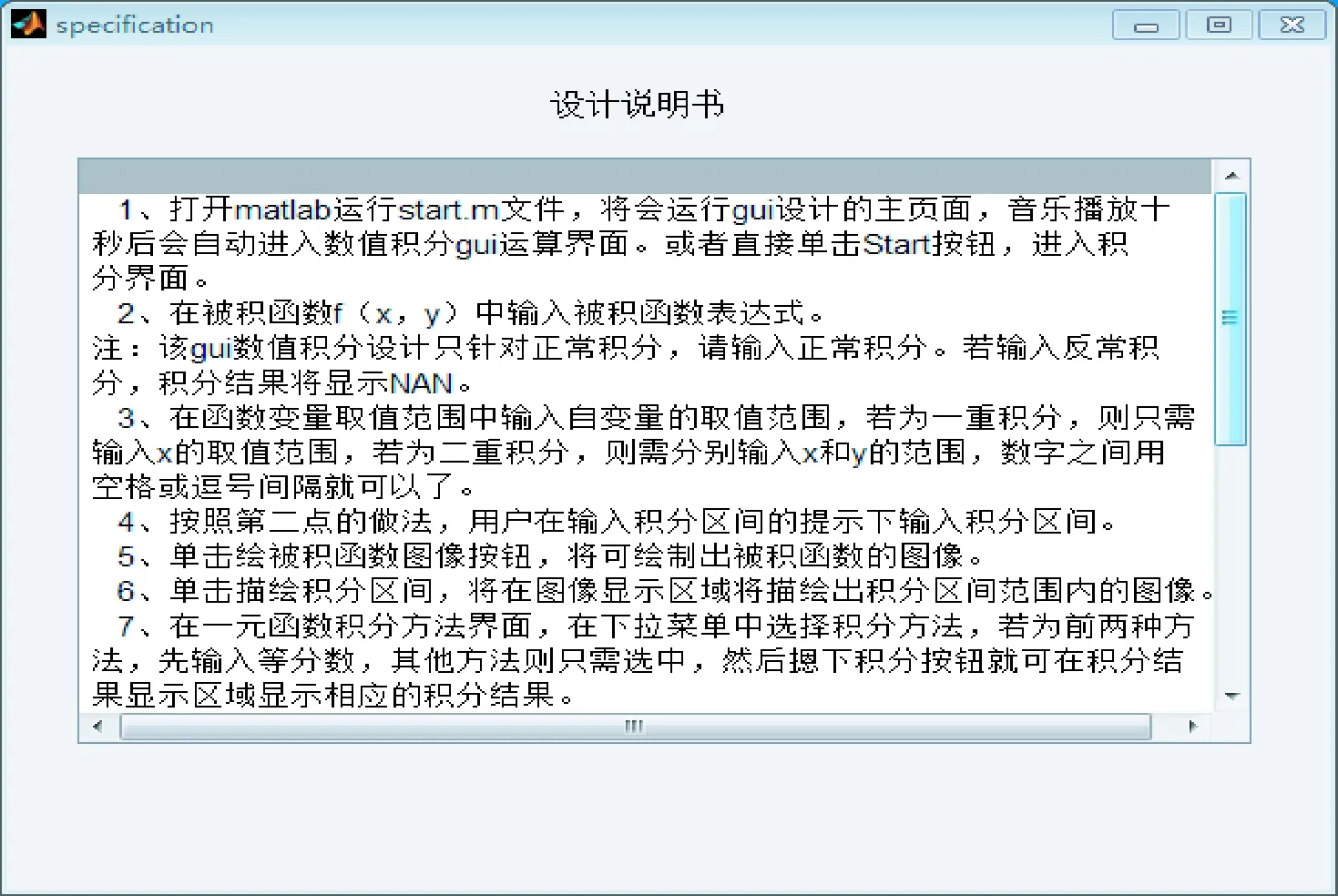
图5 GUI设计说明书
3 实例分析
Matlab-GUI积分界面主要解决数值积分理论中如下3种积分问题:求解被积函数在积分区间内解析解积分问题;求解被积函数原函数未知时的积分问题;求解即使被积函数原函数已知,但其形式非常复杂时的积分问题。对于上述问题,运用积分界面分别进行求解。
(1) 对于能够求出原函数的被积函数,并且其积分结果为的解析解的情况。运行所设计的GUI界面,比较5种数值积分方法的积分结果。
令y=sin(x),x∈(0,2π),积分区间为[0,0.5π],n=100时的结果如图6所示。

图6 计算结果显示图

积分的几何意义为曲边梯形的面积,随着所分成的子区间数目不断增加,所求积分的面积和就越来越接近被积函数在积分区间上曲边梯形的面积,其变化的动画演示过程如图7所示。
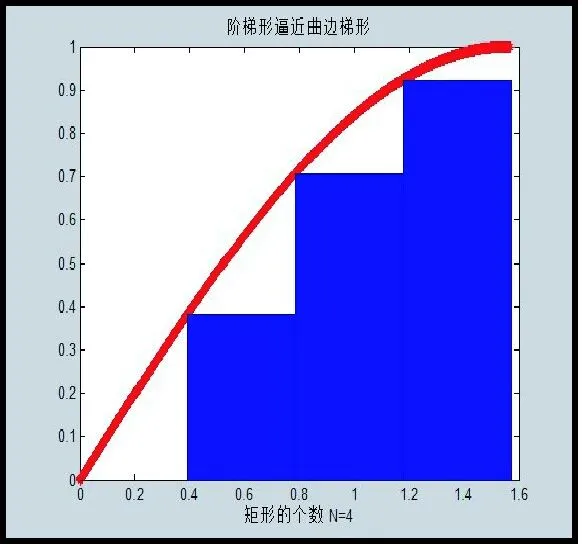
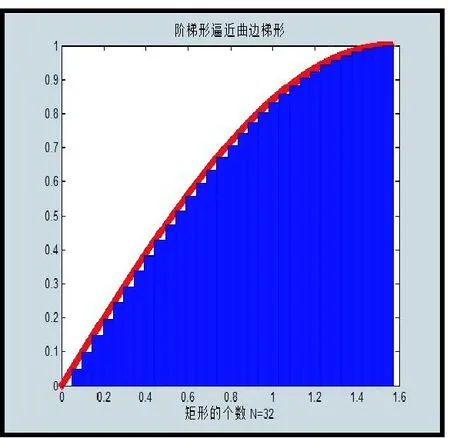
(2) 求解被积函数原函数未知情况下的积分结果。令y=sin(x)/x,x∈(1,10),积分区间为[2,7],n=100时的数值积分GUI运行结果和动画显示如图8所示。5种数值积分方法的积分结果如表1所示。


序号积分方法积分结果1Trapz-0.1507062Simpson-0.1508163CombineTrapz-0.1495044GaussLegendre-0.1508165Smart-0.151072
(3) 求解被积函数原函数已知,但原函数结构复杂因此难以求出积分结果的函数积分值。令y=1/(1+x6),x∈(-5,5),积分区间为[-2,1],n=7时的结果显示。
其原函数为:

因此很难求出其积分结果,运用数值积分GUI运行结果和动画显示如图9所示。5种数值积分方法的积分结果如表2所示。
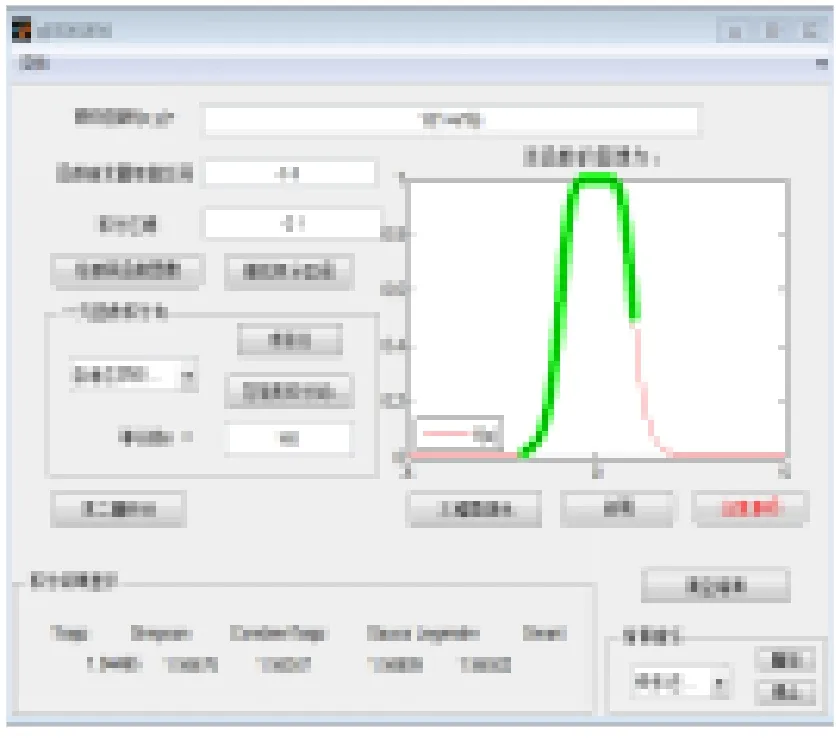

序号积分方法积分结果1Trapz1.919272Simpson1.945283CombineTrapz1.943474GaussLegendre1.946095Smart1.94502
(4) Matlab-GUI积分界面计算二重积分。当所给函数是二元函数,积分区间为体积时,便涉及到二重积分计算问题。这里采用矩形法计算二重积分。设f(x,y)=sin(x)+x·cos(y),x∈(0,3),y∈(0,3),积分区间为x∈(1,2),y∈(0,3),其运行结果如图10所示。

4 结 语
将Matlab—GUI应用于设计积分界面,设计出了GUI积分界面,为未掌握数值积分理论知识和不了解Matlab-GUI相关知识的人提供了极大的方便,为他们提供可视化的积分结果。另外,该界面使得被积函数不管为哪种积分类型,都能计算出积分结果。
仍需完善的方面是由于系统对输入法不兼容,可能导致用户在使用过程中出现一些输入法上的问题。该设计可用于工程模型及高校建模过程中涉及到的积分求解问题。
[1] 陈垚光.精通Matlab GUI设计(3版)[M].北京:电子工业出版社,2013.
[2] 鲁晓东. Visual C++与Matlab的界面混合编程[J]. 实验室研究与探索, 2011, 30(7):76-78.
[3] 张 鸣. 基于Matlab GUI的通信原理演示系统设计[J]. 实验技术与管理, 2013(9):111-113.
[4] 李 彤, 项四通, 李吉宗. 基于Matlab的材料力学图形用户界面系统开发[J]. 实验室研究与探索, 2010, 29(8):42-44.
[5] 钟可君, 张海林..基于Matlab GUI设计的光学实验仿真[J]. 实验室研究与探索, 2010, 29(10):52-53.
[6] 谢丽蓉.基于Matlab GUI异步电动机人机界面设计[J]. 实验技术与管理, 2014(8):50-53.
[7] 兰 红,田 进.基于Matlab GUI的图像处理平台设计[J]. 江西理工大学学报,2014,35(3):79-84.
[8] 曲东才, 卢建华, 谢孔树. 飞机下滑定高控制GUI设计与仿真实验[J]. 实验室研究与探索, 2015, 34(10):111-115.
[9] 杨 娟,郭海湘,杨文霞,等.基于 Matlab 的 GUI 设计车辆路径问题的仿真优化平台[J].系统仿真学报,2012, 24(3):722-727.
[10] 王红梅, 张厚升, 邢雪宁. 基于 Matlab GUI的过程控制仿真实验系统设计[J]. 山东理工大学学报(自然科学版), 2015(6):58-60.
[11] 高红兵.GUI可视化功能在求解线方程组中应用研究[J]. 内江科技,2014(11):53-54.
[12] 杨传胜, 曹金亮. Matlab大学数学实验[M]. 北京:中国人民大学出版社, 2014.
[13] 沈 静, 黄登斌. 基于Matlab的GUI在高等数学教学中的应用[J]. 高等继续教育学报, 2012(3):45-46.
[14] 唐世星. 基于Matlab的高等数学实验图形用户界面系统开发[J]. 实验室研究与探索, 2012, 31(9):202-203.
[15] 于育民,连冬艳.Matlab-GUI在数值积分中的应用[J].南阳理工学院学报,2009(6):116-120.
[16] 石学军. 基于Matlab GUI软件制作方法的研究与实现[J]. 信息系统工程, 2015(2):46-46.
The Numerical Integration Design Based on Matlab-GUI
ZHANGJian-bin,ZHAOJing,XUXiao-qing
(School of Economics and Management, Chang’an University, Xi’an 710064, China)
This paper puts forward the problem about the design of numerical integral interface, to solve the complex integral calculation under three situations: first, the function is completely unknown; second, the function is known while its form is complex; third, the function is known and the analytical solutions exist. Combining the GUI tool which can be developed in Matlab with typical algorithm in the calculation of numerical integration, this paper constructs an open users' interface, and designs the numerical integral solver even realize visualization of the numerical integration. At the same time, the thinking of using a custom way to set integral interval equivalent fractions has improved the computational accuracy of five integral methods. Finally, the designed numerical integration GUI interface is used to verify three types of complex integral function. The results show that the design can solve the integration at any set accuracy by using the five methods in the same interface, and visualizes the computed results. Therefore, the designed interface has advantages of strong adaptability, convenience, friendliness and simple operation.
numerical integration; graphical users' interfaces; Matlab; integral solver; visualization
2016-03-14
张建斌(1967-),男,陕西合阳人,博士,副教授,硕士生导师,主要研究方向:统计学;
Tel.:13909208719; E-mail:zhangjb@d.edu.cn
TP 317
A
1006-7167(2017)01-0127-05

