抗滑桩土拱效应的离散元分析

张 婧，赵 波

(1.重庆建工市政交通工程有限责任公司，重庆 400021;2. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059;3.重庆建工集团股份有限公司设计研究院，重庆 400074)

抗滑桩土拱效应的离散元分析

张 婧1，赵 波2,3

(1.重庆建工市政交通工程有限责任公司，重庆 400021;2. 成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059;3.重庆建工集团股份有限公司设计研究院，重庆 400074)

采用离散元方法对抗滑桩的土拱效应进行研究。结果表明：随着土拱效应的发育，抗滑桩的承载力随之增加，并在土拱效应最为发育时，抗滑桩的承载力达到最大，随后土拱效应遭到破坏，承载力随之降低形成残余承载力，并随着坡体的持续变位趋于稳定；随着桩间距的增大，抗滑桩的土拱效应逐渐减弱；当摩擦系数增大时，离散土颗粒之间的相互作用力增大，使得土拱效应得到增强；随着孔隙率的升高，离散土颗粒的致密性降低，使得土拱效应逐渐减弱。

抗滑桩；土拱效应；离散元；影响因素

抗滑桩以离散的修筑来实现连续的支挡，在离散实现连续的过程中土拱效应作用显著[1-3]。很多学者对土拱效应进行研究：赵明华[4]、周德培[5]、周应华[6]、杨雪强[7]、李邵军[8]等对土拱效应的力学机理进行推导和分析，得到了很多结论和公式；张永兴[9]、杨明[10]等从不同的试验角度探讨了土拱效应的存在及其作用；Chen C Y[11]，张建华[12]通过数值模拟的方法对抗滑桩的土拱效应分别进行了验证、探讨和分析。但是以上分析理论、物理实验和数值模拟等绝大部分均是考虑连续介质情况下，而现实中滑体是由大量的离散颗粒组成，具有明显的离散特征，故采用离散方法对土拱效应进行研究分析更符合实际情况。目前关于抗滑桩土拱效应的离散元分析很少，仅有向先超[13]、詹永祥[14]、李明明[15]等采用离散元对其进行了初步的分析和探讨，这些研究还远远不够。为此本课题组采用离散元软件PFC对抗滑桩的土拱效应进行探讨和分析，研究抗滑桩土拱效应从开始形成发育到最后破坏的整个过程，同时对土拱效应可能的影响因素进行分析。

1 软件及模型介绍

本文采用基于离散元理论的软件PFC2d，它是通过模拟圆形颗粒介质的运动及其相互作用来研究颗粒介质的特性，通过一种非连续的数值方法来解决含有复杂变形模式的实际问题。

抗滑桩离散元分析模型见图1。取自坡面以下z处的桩-土平面进行分析，为了简化，根据对称性取相邻两个抗滑桩中心作为计算模型边界，抗滑桩桩身横截面为方形，其边长为c=0.1 m，两榀抗滑桩间距为3c，同时为了降低加载对土拱效应的影响，抗滑桩前后各取5c的长度作为模拟长度；桩身和计算模型边界采用“墙”单元进行模拟，其中左右墙采用光滑墙体，桩前设置自由边界(不加约束)，为了模拟桩后土体的蠕变变形，桩后边界采用一个匀速运动的光滑“墙”(加载墙)，加载墙速度为0.000 5 m/s。PFC离散元计算模型见图2。为了便于观察土体颗粒的变位情况，把土体颗粒设置成不同颜色。

图1 土拱效应离散元分析模型 图2 土拱效应的离散元模型

通过颗粒流双轴试验和室内土工试验进行参数标定[16]，土颗粒的微观参数见表1。

表1 模型细观参数

2 土拱效应形成变化过程

土拱效应并不是一个位移拱而是一个力学拱，它是土体颗粒在位移变化过程中为了抵抗位移变化而自发形成的。因此，分析抗滑桩的土拱效应主要从抗滑桩桩后的力学拱效应进行分析研究。

图3为土体在蠕变过程中抗滑桩土拱效应的力链图。力链的粗细代表着颗粒间接触力的大小。由图3可知，在土体蠕变刚刚开始时，颗粒间的作用力分布相对比较均匀，看不出桩后的土拱效应(图3(a))，随着坡体蠕变的增加，在抗滑桩桩后形成一个拱形区域的力链组，此力链拱在拱脚处(抗滑桩桩背)，力链较为粗密，中间处力链较为稀松，此种特征正是抗滑桩为抵抗坡体变形而形成的土拱效应(图3(b))，随着土颗粒蠕变的不断增加此土拱效应(力链组)不断发育，并最终达到最大(图3(c))；此后由于土颗粒的蠕变超过了土拱效应所承载的极限，桩后的土拱效应逐渐被削弱，并最终基本消失(图3(d) 、图3(e))，此时说明当滑坡推力或坡体变形超过土拱效应的承载极限后，土拱效应便会遭到破坏。

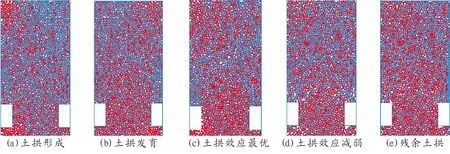
图3 抗滑桩土拱效应的形成-发育-破坏过程

图4为桩后土颗粒的位移变化图。由图4可知，抗滑桩附近的土体呈现两侧位移较小，而中间位移较大的位移拱，此位移拱与应力拱方向相反。由于左右两侧为光滑墙面，抗滑桩的前端土体为临空面，故可以认为在加载墙上荷载即为抗滑桩所承受的荷载。

图5为加载墙和抗滑桩的荷载随坡体蠕变的变化图。由图5可以看出，随着加载墙位移的增大，加载墙所承受的荷载在快速增大，这说明土拱效应正在发挥作用(对应图3(a)、图3(b))，并当加载墙位移在2.95 mm时，加载墙所承受的荷载达到最大，说明此时抗滑桩所产生的阻挡力达到最大，也说明此时土拱效应达到最强(对应图3(c))；此后随着加载墙位移的增大，作用在加载墙上荷载在逐渐降低，这说明抗滑桩的承载效果在降低，说明抗滑桩的土拱效应正在逐渐削弱(对应(图3(d))，在加载墙位移达到4.51 mm后达到最小，并且随着加载墙位移的增大，作用在加载墙的荷载保持基本不变(对应图3(e))，此时的荷载成为残余荷载。同时，左、右抗滑桩桩背面的荷载值的变化趋势与加载墙上作用的荷载变化趋势基本相同，从而可以进一步验证桩后土拱的形成-发育-破坏过程的真实性。

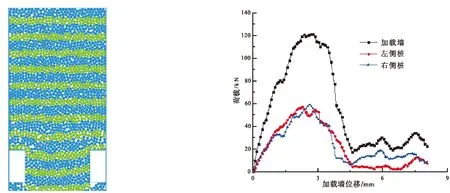
图4 土体颗粒的位移变化图 图5 加载墙和抗滑桩的荷载随坡体蠕变变化图

3 土拱效应影响因素分析

3.1 桩间距对土拱效应的影响

桩间距往往是影响抗滑桩支挡效果的主要因素。为此，考虑抗滑桩的实际布置桩间距，取n=D/d为2、3、4、5四种情况(D—两榀抗滑桩桩间距，d—抗滑桩横截面宽度)。

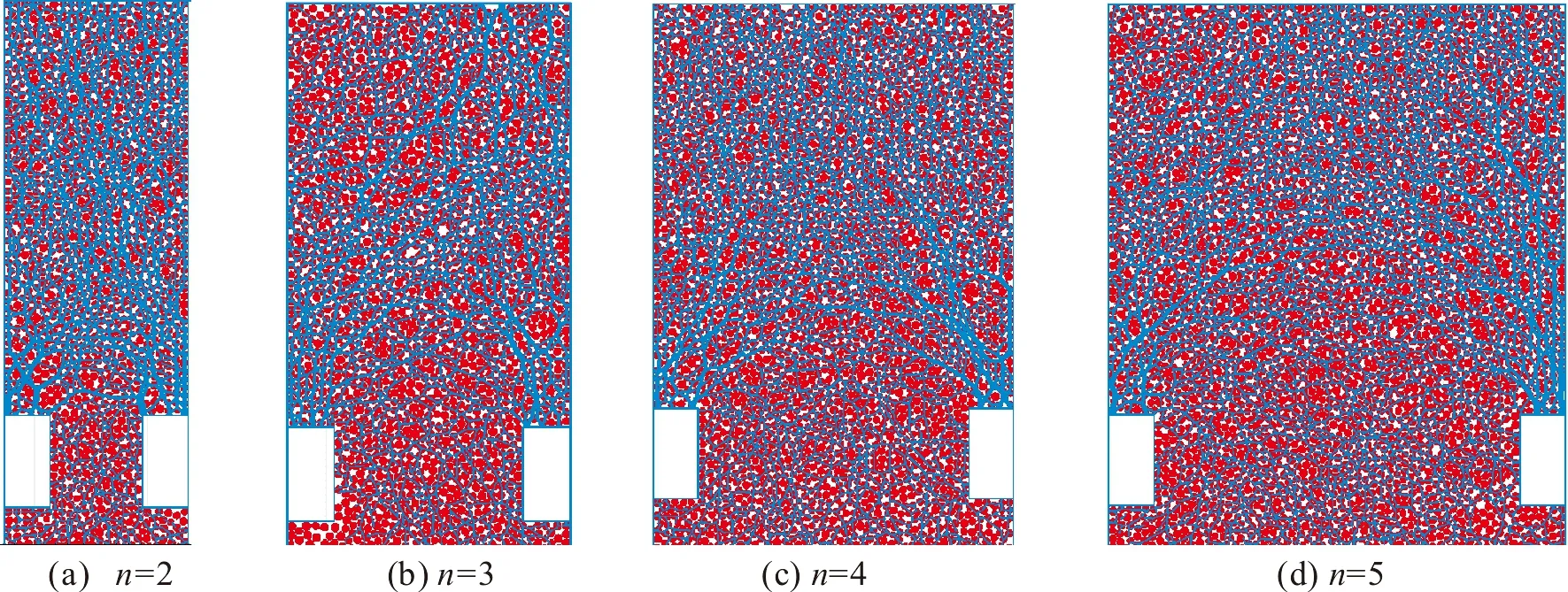
图6 不同桩间距桩后力链图

当桩间距n=2时，抗滑桩桩后的力链比较密实，桩后出现了明显的拱形力链图，说明此时桩后已经形成土拱效应，并且在发挥作用；而随着桩间距的持续增大(n=3、4、5)，抗滑桩桩后的力链拱被逐渐削弱，在桩间距n=5时，力链拱已经不明显了，说明此时桩后形成的土拱效应也相对较弱。从以上分析可知，随着抗滑桩间距的增大，桩后形成的土拱效应逐渐被削弱，也可以从侧面反映出抗滑桩支挡效果在逐渐减弱。

图7 不同桩间距下荷载变化图 图8 不同桩间距下极限荷载值

由图7可知，随着桩间距的不断增大，加载墙上作用的荷载增加幅度和所能达到的最大值均在逐渐降低，同时，达到最大荷载值土体所需要的蠕变值也在不断减小，这说明随着桩间距n的增大，抗滑桩的支挡效果在逐渐减弱。

由图8可知，随着桩间距的增大，抗滑桩的极限荷载不断降低，这与前面所得到的结果完全吻合，这说明随着桩间距的增大，抗滑桩桩后的土拱效应逐渐被削弱，抗滑桩的支挡效果逐渐降低。

3.2 摩擦系数对土拱效应的影响

土体颗粒间的摩擦系数可以反映出土颗粒的粗糙程度，不同土体具有不同的粗糙度，对抗滑桩的支挡效果有很大的影响，为此，在保证模型其他参数不变的前提下，单独改变颗粒间的摩擦系数，研究系数对土拱效应的影响。分别取摩擦系数μ=0.5、0.8、1.1、1.4四种情况进行分析。

由图9可知随着颗粒间摩擦系数的增大，桩后的力链密实度逐渐增大，同时，桩后力链拱效应也逐渐明显；根据前述，力链的粗细代表着作用力的大小，所以随着摩擦系数的增大，桩后的作用力在逐渐增大，土拱效应不断被加强，支挡效果在不断提高。

图10、图11分别表示了在不同摩擦系数下抗滑桩桩土拱的承载值和土拱极限承载值的大小。由图10、图11可知随着土体颗粒间摩擦系数的增大，土拱效应愈加明显，抗滑桩土拱的极限承载力随之增大，说明在一般情况下，土体颗粒间的摩擦系数(粗糙程度)对土拱效应影响较为明显。细观上颗粒间的摩擦系数，可以在一定程度上表征宏观松散土体的内摩擦角(内摩擦角还受到其他因素的影响)[16]。

图9 不同摩擦系数下力链图

图10 不同摩擦系数下荷载变化图 图11 不同摩擦系数下极限荷载值

3.3 密实度对土拱效应的影响

在自然条件下，土体颗粒的密实度有所不同，可以近似用土体的空隙率来表示。为此在保证模型其他条件不变的前提下，单独改变土颗粒间的孔隙率来研究(孔隙率分别取0.17、0.21)密实度对土拱效应的影响。图12为不同孔隙率下，加载墙上作用的荷载值的变化曲线图。

由图12可知，孔隙率对桩后土拱效应的影响较为显著，当孔隙率较小时，土体较为密实，可以形成较为明显的土拱效应，抗滑桩的支挡效果也相对较好；当孔隙率较大时，土体要先经历一个密实的过程，密实后才能形成土拱效应，且形成土拱后的极限承载力与较为密实时的残余承载力基本相当。

图12 不同孔隙率下荷载变化图

同时，孔隙率的大小可以反映土体的初始应力，孔隙率越小初始应力越大[16]。表层土体初始应力较低，而随深度增加初始应力逐渐增加，说明随着深度的增加，桩后的土拱效应会逐渐明显，这也说明随着深度的增大抗滑桩所起到的支挡作用越大。

4 结论

(1)随着土体颗粒的蠕变，首先会在桩背面处进行累积，造成土体颗粒不断由桩背向桩中心土体“锲紧”并最终形成土拱效应，随着“锲紧”的不断进行，土拱效应不断提高，直到达到极限，此时土拱的承载力达到极限，支挡效果达到最优，而后土拱效应遭到破坏，抗滑桩的支挡效果随之下降；土拱效应的强弱，直接决定着抗滑桩支挡效果的好坏。

(2)随着抗滑桩间距的增大，抗滑桩桩后的力链拱越来越不明显，即抗滑桩的土拱效应越来越弱，致使抗滑桩极限承载力越来越低，直接导致抗滑桩的支挡效果越来越差。

(3)土颗粒间的摩擦系数增大，滑土体的粗糙程度增大，使得桩后土体相互作用力增大，力链拱(土拱效应)越发明显，土体的极限承载力也在不断增大，抗滑桩的支挡效果在不断增大。

(4)土体颗粒越为密实，抗滑桩的土拱效应越发明显、极限承载力越大，其支挡效果也越好，同时抗滑桩下层土体的支挡效果比上层好。

[1] WANG W L,YEN B C.Soil arching in slopes[J].journal of the geotechnical engineering division ASCE,1974, 100(GT1):61-78.

[2] 贾海莉,王成华,李江宏. 关于土拱效应的几个问题[J]. 西南交通大学学报, 2003,38(4): 398-403.

[3] 蒋良潍, 黄润秋, 蒋忠信. 粘性土桩间土拱效应间与桩间距分析[J].岩土力学,2006,27(3): 445-451.

[4] 赵明华, 陈炳初, 刘建华. 考虑土拱效应的抗滑桩合理间距分析[J],中南公路工程,2006,31 (2):1-3.

[5] 周德培, 肖世国, 夏雄. 边坡工程中抗滑桩合理间距的探索[J].岩土工程学报, 2004, 26(1): 132 -135.

[6] 周应华, 周德培, 冯君. 推力桩桩间土拱几何力学特征及桩间距的确定[J].岩土力学.2006, 27(3): 455- 462

[7] 杨学强, 吉小明, 张新涛. 抗滑桩桩间土拱效应及其土拱模式分析[J].中国公路学报,2014, 27(1): 30-38.

[8] 李邵军, 陈静, 练操. 边坡桩-土相互作用的土拱力学模型与桩间距问题[J].岩土力学,2010, 31(5): 1352-1359.

[9] 张永兴, 董捷, 文海家，等. 考虑自重应力的悬臂式抗滑桩三维同效应及合理桩间距研究[J].中国公路学报, 2009, 22(2): 18-26.

[10] 杨明, 姚令侃, 王广军. 抗滑桩宽度与桩间土拱效应的影响研究[J],岩土工程学报,2007，29(10):1477-1482.

[11] CHEN C Y, MARTING R. Soil structure interaction for landslide stabilizing piles[J]. Computers and Geotechnics, 2002, 29(5): 363- 386.

[12] 张建华, 谢强, 张照秀. 抗滑桩结构的土拱效应及其数值模拟[J].岩石力学与工程学报, 2004, 23(4):699-674.

[13] 向先超, 张华, 蒋国盛, 等. 基于颗粒流的抗滑桩土拱效应研究[J]. 岩土工程学报, 2011(3):386-391.

[14] 詹永祥, 姚海林, 董启朋, 等. 松散体滑坡抗滑桩加固的土拱效应分析[J]. 上海交通大学学报, 2013, 47(9):1372-1376.

[15] 李明明, 程雪松, 郑刚. 基坑排桩桩间土拱效应的颗粒流模拟研究[J]. 三峡大学学报(自然科学版), 2012(1):46-53.

[16] 罗勇. 土工问题的颗粒流数值模拟及应用研究[D]. 杭州：浙江大学, 2007.

On soil arching effect of anti-sliding pile based on DEM

ZHANG Jing1, ZHAO Bo2,3

(1.ChongqingConstructionEngineeringMunicipalTrafficEngineeringCompany,Chongqing400000,China; 2.StateKeyLaboratoryofGeo-hazardPreventionandGeo-environmentProtection,ChengduUniversityofTechnology,Chengdu610059,China; 3.DesignandResearchInstituteofChongqingConstructionEngineeringGroupCo.Ltd.,Chongqing400000,China)

The discrete element method is used to study the soil arching effect of sliding pile considering the discrete characteristics of sliding body. The results show that with the development of soil arching effect, anti slide pile bearing capacity increases. When the soil arching effect develops, the bearing capacity of anti slide piles reaches the maximum. Then the soil arching effect is destroyed, and the bearing capacity decreases to form the residual bearing capacity. With the continuous displacement of the slope, the residual bearing capacity tends to be stable. With the increase of pile spacing, the soil arching effect of anti slide piles gradually weakened. When the friction coefficient increases, the interaction force between the discrete soil particles increases, so that the soil arching effect is enhanced. Finally, with the increase of porosity, the compactness of the dispersed soil particles decreases, which makes the soil arching effect weaken gradually.

anti-sliding piles; soil arching effect; discrete element method; influence factors

2016-07-15

国家自然科学基金(51408086)

张 婧(1989—)，女，河南许昌人，助理工程师。

1674-7046(2017)01-0041-06

10.14140/j.cnki.hncjxb.2017.01.008

TU4

A