《集合的基本运算》教学设计

张福庆

教学目的：

（1）理解并集、交集、全集、补集的概念，会用文字语言、符号语言及图形语言来描述这些概念。

（2）了解并集、交集、补集的一些简单性质，学会求两个简单集合的并集与交集，学会求给定集合的补集。

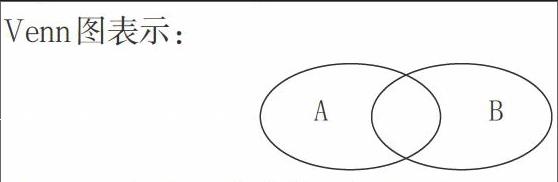
（3）能借助Venn图来探讨集合之间的关系及运算规律。

课型：新授课。

教学重点：集合的交集与并集、补集的概念。

教学难点：集合的基本运算的性质的理解与运用。

教学过程：具体如下。

一、引入课题

我们知道，实数有加法运算。类比实数的加法运算，集合是否也可以“相加”呢？

思考（书本P₆思考题），引入并集概念。

二、课堂教学

（一）并集

说明：两个集合求并集，结果还是一个集合，是由集合A与B的所有元素组成的集合（重复元素只看成一个元素）。

例题讲解（书本P₈例4、例5）。

说明：连续的（用不等式表示的）实数集合可以用数轴上的一段封闭曲线来表示。

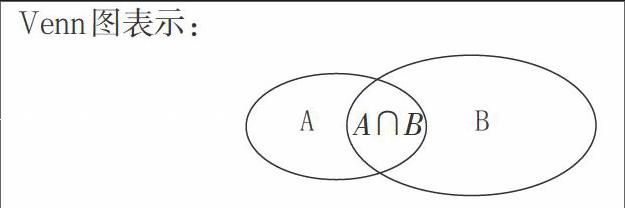
（二）交集

一般地，由属于集合A且属于集合B的所有元素组成的集合，称为集合A与B的交集。

说明：两个集合求交集，结果还是一个集合，是由集合A与B的公共元素组成的集合。

例题讲解（书本p₀例6、例7）。

说明：当两个集合没有公共元素时，两个集合的交集是空集，而不能说两个集合没有交集。

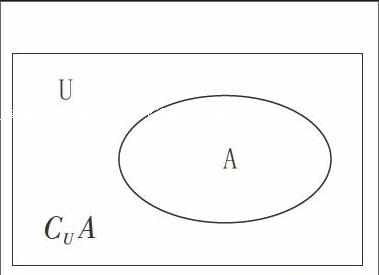
（三）补集

全集：一般地，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集，通常记作u。

说明：补集的概念必须要有全集的限制。

例题讲解（P₁₁例8、例9）。

1.知识小结。求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法。

三、归纳小结

（1）理解两个集合交集与并集的概念和性质。

（2）求兩个集合的交集与并集，常用数轴法和图示法。

（3）注意灵活、准确地运用集合的运算性质解题。

四、作业布置

作业：P₁₃习题1.1，第6、7、10题