像移残差对图像技术调焦的影响

（海军航空工程学院青岛校区，山东 青岛 266041）

像移残差对图像技术调焦的影响

李明珠，张玉叶，徐国锋，王颖颖

（海军航空工程学院青岛校区，山东 青岛 266041）

像移残差是影响航空相机图像质量的重要因素，应用图像法对航空相机实时检调焦过程中，由于像移残差的存在，调焦精度降低。当前关于像移残差和调焦精度两者的之间关系没有通用性的理论性研究。从理论上分析了航空图像线性像移残差模型，给出了像移残差模型对评价函数的影响，得到像移残差与调焦曲线极大值呈负相关的关系。图像的像移残差量越大，调焦函数曲线的最大值下降越显著。

像移残差；图像技术；调焦精度

航空相机在实际像移补偿过程中，由于速高比、扫描角姿态角、飞机姿态角度存在引入误差，以及补偿控制系统性能及补偿精度的影响，所拍摄的图像往往会存在像移残差。然而，航空相机应用基于图像处理技术的检调焦方法时，往往直接使用航空相机获取到的图像，因此该方法对图像质量的依赖性较强。带有像移残差的图像往往图像质量不高，它会导致应用基于图像法检调焦时，系统的调焦准确率下降。因此像移残差的存在对高分辨率航空图像实时检调焦技术的影响不可忽略。研究像移残差对航空相机实时检调焦技术的影响有重要的意义。

1 航空相机像移残差

航空相机在拍摄过程中，由于受飞行运动、姿态运动的影响产生像移，其中横向像移由飞机横滚角速度ϕ′产生，飞行纵向像移是由飞行速度ν、偏流角速度ψ′、俯仰角速度θ′产生。在航空相机工作状态下，飞机保持匀速平直飞行，姿态角变化不大于±5°，对于摆扫成像的TDICCD相机，纵向像移速度xν、横向像移速度yν可近似表示为：

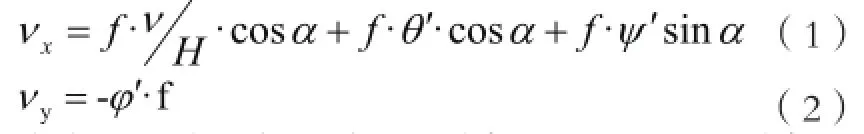
式中，v为飞行速度；f为相机焦距；α为相机摆扫角度；H为飞行高度。

航空相机拍照时，通过控制扫描反射镜的摆动速度补偿纵向像移。由于反射镜反射光线的变化角度与其入射光线转动角度成2倍关系，因此当反射镜摆动角速度为时，所产生的像移补偿速度由式(1)可得补偿角速度为

飞机横滚角速度引起的横向像移可以通过TDICCD行转移频率控制实现补偿，随着横滚角速度的变化，由式（2）可得到行转移频率增加的补偿转移频率fm为：

式中， b为像元尺寸。

经过理论分析可知，航空相机产生的横向和纵向相移可以获得完全补偿，但是在实际的像移补偿过程中，由于存在数据的引入误差，如速高比v/H、扫描角姿态角α等等，以及补偿控制系统精度的影响，导致系统的最终补偿结果存在误差。纵向补偿速度误差以及横向补偿速度误差分别用表示，曝光时间t内产生的剩余像移量称为像移补偿残差δ（简称像移残差），像移残差的存在使成像质量下降，同时也对后续图像技术调焦精度造成影响。

2 像移补偿残差对评价函数的影响

2.1 图像调焦评价函数模型

一幅良好的航空图像应包含有丰富的细节和清晰的边缘信息。因此，航空相机在自动调焦时通常采用提取图像中的边缘和细节部分，并依据这些信息作为评价图像是否清晰的依据。图像的细节和边缘信息经过频域变换后成为频谱中的高频部分。变换后的频谱图像如果含有较多的高频分量，则说明图像本身成像质量较好。因此，一幅图像清晰度的判断可以通过检测这幅图像傅里叶变换频谱中的高频信息是否丰富来实现。假设一幅图像表示为则图像的调焦评价函数可以表示为：

区间(ξ1，ξ2)表示频谱中的高频分量区间。

2.2 航空图像线性像移残差对评价函数的影响

在分析图像像移残差对航空相机自动调焦的影响时,垂直于成像平面的z轴方向上也会存在像移，并对图像质量造成影响。如果相机系统控制精度不高，z轴像移也会导致图像放大倍率的改变，同时距离的变化也会影响离焦量的大小。而对于长焦距航空相机来讲，相机成像距离远，所以z轴像移及像移残差的影响非常小，可以忽略不计。因此，往往只考虑x-y平面上像移残差而忽略z轴方向的影响。

航空图像的线性像移残差只在移动方向上使图像产生拖尾效应，而在垂直于飞机移动方向上对图像质量没有影响。线性像移残差的模型可以看作是图像在像移残差方向上与矩形函数的卷积：

当航空相机检调焦控制系统利用图像法进行调焦时，通过计算相机获取图像的评价函数值，得到像的调焦评价函数曲线，评价曲线最高点对应的位置即为图像对焦最佳点。为了计算图像的评价函数曲线，选择图像傅里叶变换后频谱中的高频分量作为评价函数，当系统存在线性像移残差时，计算有残差图像的傅里叶变换，得到：

式中矩形函数h (x,y)的傅里叶变换函数为sinc函数

针对航空图像存在的线性像移残差，残差只在一个方向上，因此，可以简化为由此可见，有残差的图像经过傅里叶变换后频谱中频率分量与无残差图像的频率相同，但频谱中增加了函数项，频率的权重改变了。图像经过傅里叶变换后频谱分量不变，但每个频率分量都乘以函数。因此，频率值越大的函数曲线下降越快，频谱中的高频分量与函数相乘后下降的更明显。函数只与像移残差δ相关，对于有相同像移残差的图像，图像质量下降的程度是相同。

3 残差对图像调焦精度分析

当航空相机焦面位置不同时，图像所对应的离焦量不相同，评价函数值也不同，选择图像傅里叶变换后频谱中的高频分量信息作为评价函数，在控制系统应用基于图像处理技术的调焦方法时，函数曲线上两点之间的差值表示两幅航空图像清晰度的差异。当系统无残差存在时，两幅图像评价函数差值Δ表示为：

当相机控制系统在补偿后依然存在残差时，航空图像经傅里叶变换后频谱中多了与残差的有关项。假设系统的像移为线性像移，残差也为线性，图像傅里叶变换后评价函数差值的结果可表示为：

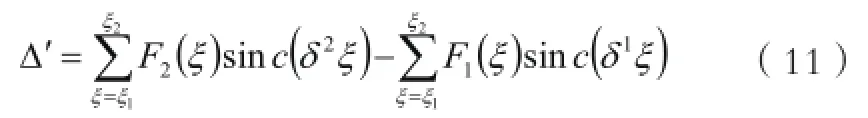
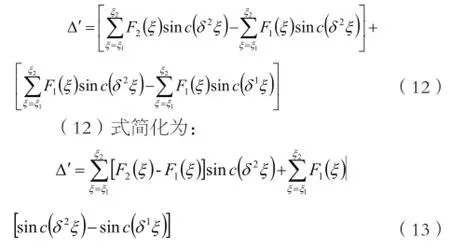
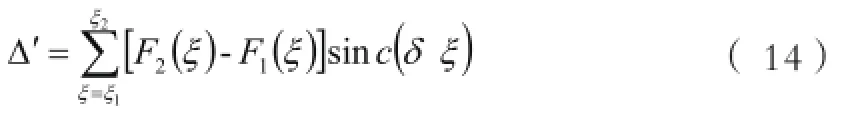
如图1所示，当系统存在像移残差时，评价函数差值的结果多了函数项，该项的影响使得频评价函数的差值变小，评价函数曲线趋于平滑，但函数曲线的峰值位置不改变，对最终的调焦结果并无影响。如图2所示，当两幅图像的像移残差量接近时，则对评价函数差值的影响越小，此时的调焦结果愈加接近图像像移残差相同时的调焦结果，如果两幅图像的残差量不相同，则(13)式中第二项差值不为零，该项数值受到图像残差量大小的影响。当两幅图像的像移残差量相差较大时，(13）式中第二项的值也较大，对评价函数差值的影响也越大，图像法调焦结果不准确。

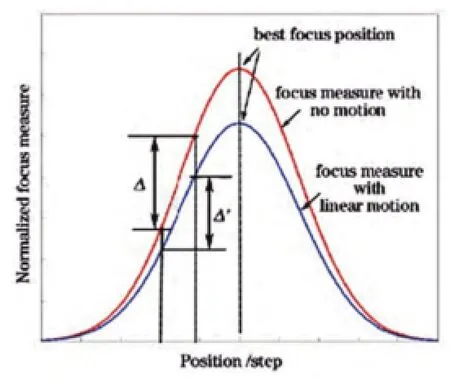
图1 像移残差图像评价函数曲线图

图2 不同像移残差sinc函数差值曲线

4 结语

针对航空相机在像移补偿后依然存在像移残差的现象，分析了像移残差对图像法调焦精度的影响。通过分析建立的控制系统线性像移残差模型，从理论上分析存在残差时对调焦评价函数的影响。系统像移残差量越大，评价函数曲线下降越明显，图像法调焦结果的准确性越差。

[1]孟繁浩，丁亚林，王德江等.像移对长焦距高分辨率航空相机检调焦精度影响的分析[J].光学学报，2015,35(6):0611001-1- 0611001-8.

[2]李英杰，李开端. 图像频谱分析在像移残差检测中的应用[J].四川兵工学报，2015,36(7):86-89.

TP391.41

：A

：1671-0711（2017）04（上）-0135-03