住院患儿医院感染发生率ARIMA时间序列模型
刘海鹏,金玉莲,刘光辉,倪 虹,张秀平,崔 伟
(安徽省儿童医院,安徽 合肥 230051)
·论著·
住院患儿医院感染发生率ARIMA时间序列模型
刘海鹏,金玉莲,刘光辉,倪 虹,张秀平,崔 伟
(安徽省儿童医院,安徽 合肥 230051)
目的 初步探索和评价儿童患者医院感染发生率的自回归滑动平均混合模型(ARIMA)预测模型。方法 以某院2011年1月—2014年12月4年医院感染发生率数据建立ARIMA模型,依据信息量准则,确定最优模型;以2015年医院感染发生率数据作为验证样本,评价模型的可行性。结果 ARIMA(0,1,1)为医院感染率最优预测模型,其最小信息量准则(AIC)、贝叶斯信息准则(BIC)值分别为66.61、70.76,模型残差序列的Ljung-Box统计量Q=14.14,差异无统计学意义(P=0.658),提示残差为白噪声序列,模型拟合良好。医院感染率实际值与预测值的平均绝对百分误差值(MAPE)为22.4,实际值均在预测值95%可信区间内,未见超出点。结论 ARIMA时间序列模型拟合医院感染率效果良好,具有预测住院患儿医院感染发生情况的实际价值。
儿童; 医院感染; ARIMA模型; 预测
[Chin J Infect Control,2017,16(3):243-246]
世界范围内,医院感染都是威胁患者安全的最常见不良事件。患者在接受住院医疗服务时发生感染,导致患者病情加重,住院时间延长,死亡风险相应增加,此种情况在发展中国家更明显[1]。儿童由于各系统和器官发育尚未成熟,各种生理功能尚未完善,免疫机制尚不健全,对大多数致病病原体抵抗力弱,特别是呼吸道病原体,获得医院感染的机会更大[2]。了解儿童患者医院感染发生发展规律,并在此基础上采取可能的预防措施尤为重要。有学者采用时间序列等方法进行分析,预测成人综合性医院医院感染现患率发生发展规律[3-4];也有学者通过横断面调查方法描述儿童专科医院的医院感染发生情况[5-6],但是尚未见住院患儿医院感染情况的预测研究。本研究回顾分析一所省级儿童医院近4年医院感染月度现患率数据,应用自回归滑动平均混合模型(autoregressive integrated moving average model,ARIMA)时间序列模型方法进行分析,试图探索一种医院感染发生率新预测模型,为住院患儿医院感染预防关口前移提供新的思路和方法。
1 对象与方法
1.1 资料来源 收集2011年1月—2015年12月安徽省儿童医院相关临床科室上报并经感染管理科专职人员确认的住院患儿实际发生医院感染例次数据,以及汇总形成的月度医院感染发生率数据。
1.2 诊断标准 以卫生部2001年颁布的《医院感染诊断标准(试行)》为医院感染诊断依据。
1.3 ARIMA模型构建 ARIMA是Box-Jenkins方法中的重要时间序列分析预测模型[7]。该模型试图应用相应的数学模型,将预测对象随时间推移形成的数据序列描述出来,并在该基础上选择合适的模型进行预测。实际运用中,首先通过平稳性和纯随机性检验进行序列预处理,然后确定ARIMA(p、d、q)模型中的3个参数,其中p为自回归的阶,d为差分次数的阶,q为滑动平均的阶,最后通过残差序列检验拟合模型是否有效,并可通过最小信息量准则(Akaike information criterion,AIC)和贝叶斯信准则(Bayesian information criterion,BIC)判断多个模型中最优模型。
1.4 建模分析方法 应用SPSS16软件ARIMA 模块进行建模和分析,以2011—2014年月度医院感染发生率数据作为训练样本,以2015年数据作为验证样本。
2 结果
2.1 医院感染情况 2011—2015年分月统计医院感染发生率,范围为0.58%~2.6%,结果见图1。
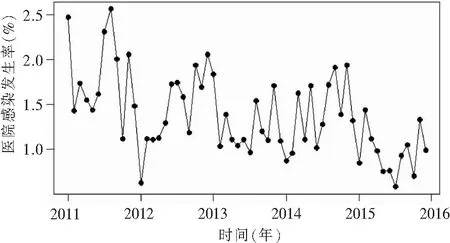
图1 2011—2015年月度医院感染发生率(%)
2.2 模型定阶 应用ARIMA方法的前提条件是作为预测对象的时间序列是零均值的平稳随机序列。对原序列作线图,发现2011—2014年数据变异较大,因此首先对数据采取差分,以平稳序列的方差。对原序列进行一阶差分经过差分后得到的相关图及偏相关图见图2。同时依据信息量准则判断模型的优劣,见表1。比较各模型信息量准则,最终确定ARIMA(0,1,1)为最优模型。

图2 医院感染差分后序列自相关图与偏相关图
Table 1 Comparison of goodness of fit among different ARIMA models
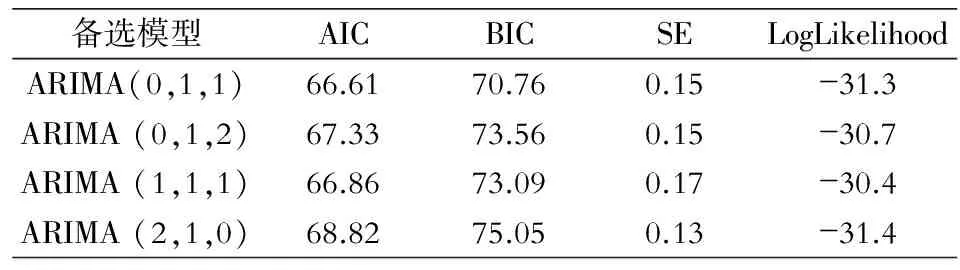
备选模型AICBICSELogLikelihoodARIMA(0,1,1)66.6170.760.15-31.3ARIMA(0,1,2)67.3373.560.15-30.7ARIMA(1,1,1)66.8673.090.17-30.4ARIMA(2,1,0)68.8275.050.13-31.4
2.3 模型诊断 对模型进行检验,对完整模型的残差再次做ACF (autocorrelation factor)和PACF (partial autocorrelation factor) 分析。模型拟合统计量R2=0.77,残差序列的Ljung-Box统计量Q=14.14,差异无统计学意义(P=0.658),显示残差是白噪声序列,模型拟合较好。2011—2014年医院感染发生率实际值与拟合值的平均绝对百分误差值(Mean Absolute Percent Error,MAPE)为22.4,对应的拟合图见图3,可见拟合值和实际值匹配较好,实际值均在拟合值95%可信区间内,未见超出点,模型效果比较理想。
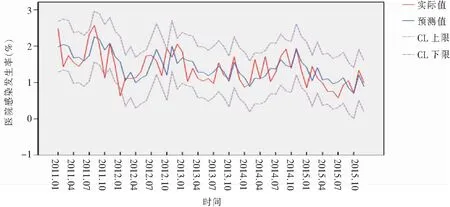
图3 医院感染发生率实际值与ARIMA模型拟合值匹配图
2.4 模型预测 2015年月度医院感染发生率实际值与模型预测值比较,结果见表2。模型预测值的动态趋势与实际情况基本一致,各月实测值均位于预测值95%可信区间范围。
表2 2015年1—12月医院感染发生率实际值与预测值比较
Table 2 Comparison of the incidence of HAI between actual value and predictive value in January-December, 2015
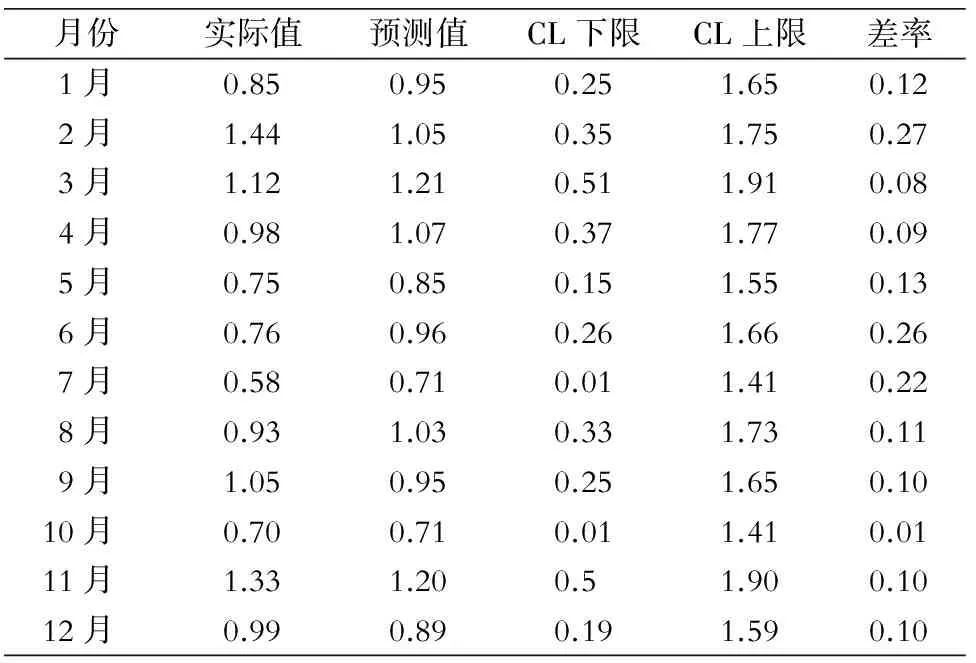
月份实际值预测值CL下限CL上限差率1月0.850.950.251.650.122月1.441.050.351.750.273月1.121.210.511.910.084月0.981.070.371.770.095月0.750.850.151.550.136月0.760.960.261.660.267月0.580.710.011.410.228月0.931.030.331.730.119月1.050.950.251.650.1010月0.700.710.011.410.0111月1.331.200.51.900.1012月0.990.890.191.590.10
差率=(|实际值-预测值|)/实际值
3 讨论
医院感染的发生会给患儿和家庭,以及医院带来额外的负担。卫生部于2006年颁布《医院感染管理办法》,明确要求开展医院感染监测,为医院感染控制提供科学依据。近年来,针对医院感染发病情况进行前瞻性预测也成为了一个重要的研究方向,核心目的是主动监测,发现和干预医院感染危险因素,进一步降低患者医院感染风险。时间序列线性模型、人工神经网络模型、灰色模型等方法均已逐渐应用于医院感染危险度的预测研究中,并取得了一定的成果[8-9]。
ARIMA时间序列模型[ARIMA(p, d, q)]是Box-Jenkins方法中的重要时间序列分析预测模型,也称为自回归滑动平均混合模型。通过分析时间序列的随机性、平稳性,可以识别出最适宜模型,并可以利用时间序列的过去值、现在值,预测未来值。
本研究应用ARIMA时间序列模型分析医院感染发生率,综合考虑了序列的随机性、平稳性、周期性等因素的影响,依据不同模型信息量准则的比较筛选,基于4年的数据优选出适宜的预测模型ARIMA(0,1,1)。使用当前模型对2015年数据进行预测,发现实际值与预测值重合较好,实际值均在预测值95%可信区间内,预测拟合效果较可靠。而且,对当前模型进行拟合优度检验,残差序列的Ljung-Box统计量Q=14.14,残差值达到白噪声序列,也显示预测拟合结果较好。
本研究的结果亦需要更多的医院感染发生率实际数据进一步验证。同时,为增强模型预测的稳定性和准确性,未来也需要更多的数据积累,进一步修正和优化,直至拟合出更加稳定的ARIMA预测模型。由于医院感染的发生是诸多因素综合影响的结果,我们也会尝试将其他影响因素的作用融入建模过程,并结合多种预测方法进行综合分析,以期为实现医院感染控制“零级预防”目标提供可量化、更可靠的管理工具。
[1] Allegranzi B, Bagheri Nejad S, Combescure C, et al. Burden of endemic health-care-associated infection in developing countries: systematic review and meta-analysis[J]. Lancet, 2011, 377(9761): 228-241.
[2] 蒋最明,彭俊,顾敏,等.1 410例儿童呼吸道感染病原体分析[J].中国感染控制杂志, 2013, 12(2): 129-131.
[3] 李红,梁沛枫,潘东峰,等.自回归滑动平均混合模型在医院感染发病率预测中的应用研究[J].中华医院感染学杂志,2013,23(11):2693-2695.
[4] 管利华.ARIMA模型预测医院感染发病状况研究[J].实用预防医学, 2013,20(10):1247-1249.
[5] 印爱珍,马乐龙,邓莉,等.儿童医院医院感染横断面调查[J].中国感染控制杂志, 2015, 14(11):769-771.
[6] 张艳丽,周新歌,孙琳,等.2014年某儿童医院医院感染现患率调查[J].中国感染控制杂志,2015,14(9):629-632.
[7] 孙振球.医学统计学[M].3版.北京:人民卫生出版社,2005: 390-393.
[8] 陈立兵,刘运喜,杜明梅,等.BP神经网络在预测血液病患者医院感染中的应用[J].中华医院感染学杂志, 2014,24(6):1542-1544.
[9] 李红,潘东峰,郭忠琴,等.灰色GM(1, 1)模型在医院感染发病率预测中的应用[J].宁夏医学杂志, 2013, 35(3): 221-223.
(本文编辑:付陈超)
Construction of ARIMA time series model for healthcare-associated infection in hospitalized children
LIUHai-peng,JINYu-lian,LIUGuang-hui,NIHong,ZHANGXiu-ping,CUIWei
(AnhuiProvincialChildren’sHospital,Hefei230051,China)
Objective To investigate the applicability of autoregressive integrated moving average (ARIMA) model in predicting healthcare-associated infection(HAI) in children. Methods The ARIMA model was constructed according to the incidence of HAI in a hospital from January 2011 to December 2014. With the use of information criterion, optimal model was determined; HAI data in 2015 was as test samples, the feasibility of the model was evaluated. Results ARIMA (0,1,1) was the optimal prediction model for HAI rate, the Akaike Information Criterion(AIC)and Bayesian Information Criterion(BIC)of the ARIMA(0,1,1) were 66.61 and 70.76, respectively. The Ljung-Box statistics valueQ= 14.14 was not significantly different (P= 0.658), suggesting a white noise sequence of residuals with a good model fitting. The mean absolute percent error(MAPE) between actual and fitting value of HAI was 22.4, the actual values were within the 95% confidence interval. Conclusion ARIMA model fits the time series data, and can achieve satisfactory effect on predicting the incidence of HAI in hospitalized children.
child; healthcare-associated infection; ARIMA model; predict
2016-05-30
安徽省2016年软科学研究专项(1607a0202055);北京儿童医院集团2015年度科研课题(北儿集团学字[2015]33号(01))
刘海鹏(1970-),男(汉族),安徽省合肥市人,主治医师,副研究员,主要从事儿科与医院感染管理研究。
金玉莲 E-mail:etyykejiaoke@126.com
10.3969/j.issn.1671-9638.2017.03.014
R181.3+2
A
1671-9638(2017)03-0243-04

