通缝拼装盾构隧道横向刚度有效率计算方法及其影响因素

黄大维，周顺华，冯青松，狄宏规，舒　瑶

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌　330013；2.同济大学 道路与交通工程教育部重点实验室，上海　201804)

目前，国内外研究人员主要采用梁—弹簧模型和修正均质圆环模型(修正惯用法)对地铁盾构隧道进行横向内力与变形分析[1-2]。在梁—弹簧模型中，将管片纵缝接头等效为包括具有剪切刚度、拉压刚度及转动刚度的三维弹簧，这与管片环的实际性能最为接近，其关键参数为纵缝接头刚度k。既有关于k的研究主要集中在对k的影响因素[3-5]及k对隧道横向内力与变形结果的影响[6-9]，两方面研究方法有数值仿真、理论分析与模型试验，但由于研究方法自身的局限性导致结果存在不同程度的偏差。同时，梁—弹簧模型的建模过程相对复杂。修正均质圆环模型的建模过程相对较为简单，其关键参数为横向刚度有效率η。现有对η的研究主要集中在η的取值[10-12]及对η的影响因素[13-14]两方面，研究手段以理论分析和模型试验为主。在确定η的取值过程中，一般可选用修正均质圆环模型的水平或竖向收敛变形与对应的梁—弹簧模型[15]或模型试验实测的收敛变形[16-17]相等作为依据，但更多的是凭经验确定。采用这些方法确定η的取值，要么过程复杂，要么缺乏理论依据。同时，现有的η与管片环直径、管片厚度、管片环接头数量等参数之间的关系式都是基于曲线拟合所得的计算公式[14,18]，并无明确关系的解析表达式，更没有建立η与纵缝接头刚度k之间的关系式，因此有必要对上述问题展开研究。

本文基于η的定义，分析k与η之间的关系，推导根据k计算η的公式；通过对梁—弹簧模型与修正均质圆环模型仿真所得变形结果的比较，验证η计算公式的可行性；根据推导的η计算公式，分析η的影响因素。

1　通缝拼装盾构隧道横向刚度有效率计算

将η定义为修正均质圆环的横向截面抗弯刚度E′I′与拼装管片环横向截面抗弯刚度EI的比值，即

(1)

式中：E′为修正均质圆环的弹性模量；I′为修正均质圆环横向截面的惯性矩；E为拼装管片环的弹性模量；I为拼装管片环横向截面的惯性矩。

由于确定修正均质圆环的抗弯刚度E′I′比较困难，也没有成熟的方法，因此以往主要凭经验确定。本文基于η的定义，通过评价修正均质圆环与拼装管片环横向抗弯性能的等效性(管片环为曲梁结构，弯矩导致管片环的变形为其主要变形)，推导η的计算公式。

当拼装管片环与修正均质圆环的刚度等效时，修正均质圆环模型所有截面抗弯刚度均相同，则这2种环形结构的位移具有等效性，且这2种环形结构均为超静定结构(其超静定次数为3)。因此，将拼装管片环和修正均质圆环均从拱底块中间位置(图1(a)中的180°位置)切断，即解除3个约束，使其结构变为静定结构，再将其展开成为直梁；以两者的展开直梁两端在纯弯矩作用下具有相同的相对转角位移作为这2种环形结构刚度等效的条件，计算修正均质圆环的横向截面抗弯刚度与拼装管片环的横向截面抗弯刚度之比，此比值即为η。

以上海通缝拼装盾构隧道的管片环为例，拼装管片环和均质圆环及其展开直梁如图1所示。图1中：D1和D2分别为拼装管片环的外径和内径；h为管片的厚度；L为拼装管片环展开直梁的长度；D1′和D2′分别为修正均质圆环的外径与内径；h′为修正均质圆环的厚度；L′为修正均质圆环展开直梁的长度。

图1　拼装管片环与修正均质圆环及其展开直梁

以拼装管片环外径与内径的平均值作为直径计算拼装管片环的周长，以此作为拼装管片环展开直梁的长度，即

(2)

由胡克定律可知，直梁在弯矩M作用下的弹性弯曲应变(即单位长度发生的转角)κ为

(3)

拼装管片环展开直梁在两端弯矩M作用下其两端的相对转角是由2种因素导致的：一是直梁的弯曲，二是纵缝接头的转角。其中，因直梁的弯曲导致直梁两端截面产生的相对转角θ1为

(4)

因1个刚度为k1的纵缝接头转角导致直梁两端截面产生的相对转角θ2′为

(5)

图1中的拼装管片环展开直梁包括6个纵缝接头，其中拱顶块两边2个纵缝接头的刚度均为k1，拱腰部2个纵缝接头的刚度均为k2，拱底块两边2个纵缝接头的刚度均为k3；则6个纵缝接头转角导致直梁两端截面产生的相对转角θ2为

(6)

因此，拼装管片环展开直梁在两端弯矩M作用下其两端截面产生的相对转角θ为

(7)

对于修正均质圆环，其展开直梁在两端弯矩M作用下其两端截面所产生的相对转角θ′为

(8)

修正均质圆环与拼装管片环的刚度等效条件为：两者展开直梁在相同弯矩作用下两端截面产生相同的相对转角，即θ=θ′。因此由式(7)和式(8)可得

(9)

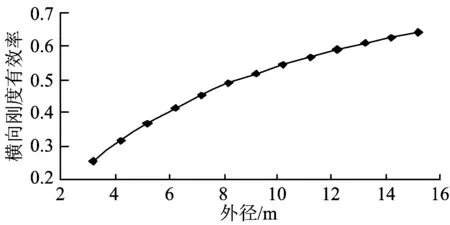
可采用2种方法将拼装管片环截面的抗弯刚度EI折减得到修正均质圆环的截面抗弯刚度E′I′：第1种方法，保持横向截面惯性矩不变，即I′=I，减小管片的弹性模量，即E′

对于第1种方法，修正均质圆环与拼装管片环的几何尺寸完全相同，即L′=L。由式(9)可得

(10)

根据式(1)和式(10)可得

(11)

对于第2种方法，可近似地认为L′=L，由等式(9)可得

(12)

同样，根据式(1)和式(12)可得

(13)

对比式(11)与式(13)发现两式完全相同，说明无论是减小拼装管片环的弹性模量还是减小拼装管片环的截面惯性矩，拼装管片环横向刚度有效率的计算式是相同的。

一般的，当拼装管片环由n个接头组成时，根据式(13)可得η的计算公式为

(14)

式中：ki为拼装管片环第i个纵缝的接头刚度；n为拼装管片环的纵缝数量，也即拼装管片环的分块数。

2　计算公式的验证分析

仍以图1(a)所示的上海地铁盾构隧道通缝拼装管片环为例，验证式(14)的可行性。

2.1　管片纵缝接头刚度确定

隧道外径为6.2 m，管片厚度为0.35 m，管片宽度为1.2 m。管片采用高强混凝土制成，其强度等级为C55，弹性模量为35.5 GPa，泊松比为0.18。管片环由6块管片拼接而成，管片间均采用M30直螺栓连接，直螺栓的机械性能等级为5.8级。

足尺试验：通过24个均匀分布的加载点施加集中荷载来模拟盾构隧道周围土体的分布荷载，将24个加载点分成3组，其中6个加载点的荷载为P1，10个加载点的荷载为P2，8个加载点的荷载为P3，如图2所示[19]。加载过程中：P2=0.5P1，P3=0.5(P1+P2)=0.75P1；P1的加载过程：从0开始，每级荷载增量为15 kN，分为10级，直至150 kN；然后，每级荷载增量减小为5 kN，直至结构发生破坏。选取其中的4个加载工况进行分析，详见表1。

图2　集中荷载分布与管片环分块方式[19]

表1　足尺试验中不同加载工况对应的理论加载值

位移测点分别布设在0°，74°，105°，180°，255°，286°位置处，共有6个测点；位移均为径向位移，以测点向外侧移动为正、向圆中心方向移动为负。

在荷载足尺试验加载过程中，针对4个加载工况，实测的荷载加载值和6个测点的径向位移见表2[19]。对比表1和表2可知，荷载的实测加载值与理论加载值稍有偏差，但偏差很小。

表2　足尺试验中不同加载工况下实测的荷载和位移[19]

基于足尺试验得到4个加载工况下的实测荷载与径向位移，利用数值仿真方法反演计算管片纵缝接头刚度，计算分为以下2步。

第1步，采用ANSYS有限元软件建立盾构隧道管片环结构的梁—弹簧模型。模型含有结点366个，曲梁单元360个，弹簧单元6个，且弹簧单元只考虑转动刚度；考虑到隧道结构与荷载的对称性，设8°和352°位置的管片纵缝接头刚度为k1，73°和287°位置的管片纵缝接头刚度为k2，138°和222°位置的管片纵缝接头刚度为k3，即转动刚度为k1，k2，k3的各有2个；在0°和180°位置(即顶部与底部)加水平向约束，在90°和270°位置加竖向约束，如图3所示。

第2步，根据建立的梁—弹簧模型进行反演计算。数值模型所施加的荷载采用4个加载工况下的实测荷载；由已有的研究成果可知[1]，接头抗弯刚度的数量级约为106～107N·m·rad-1，故基于此数量级不断调整管片接头抗弯刚度k1，k2，k3的取值；采用建立的梁-弹簧模型反演计算6个测点的径向位移，直至与表2中各测点的实测径向位移接近(反演计算得到的最终位移见表3)，此时对应的管片纵缝接头抗弯刚度就是该加载工况下的管片纵缝接头刚度，详见表4。同时得到了接头位置的弯矩和轴力，也列于表4中。

图3　梁—弹簧模型

表3　反演分析得到不同加载工况下的位移

表4　反演分析得到不同加载工况下管片纵缝接头的刚度、弯矩、轴力

由表4可知，随着加载荷载的增加，管片纵缝接头刚度呈现出非线性变化。在加载过程中，影响管片纵缝接头刚度主要因素为接头的内力(如接头处的轴力、弯矩)。因此，盾构隧道横向刚度有效率与地层的土体力学性能和隧道埋深有关，是因为在不同地层和不同隧道埋深状态下，盾构隧道受到的土压力不同，所以管片纵缝接头处的内力也不同，从而使得管片纵缝接头刚度不同，最终导致盾构隧道横向刚度有效率不同。

2.2　计算公式的验证

分别取E=3.55×104MPa，I=4.287 5×10-3m4，n=6；管片接头刚度按照表4取值；针对4种加载工况，采用式(14)分别计算可得η=0.415，0.212，0.103，0.072。施加足尺试验中4种加载工况下的实测荷载，分别采用梁—弹簧模型和修正均质圆环模型模拟计算结构的变形，结果如图4所示(为了更明显地看到结构变形的形态，将结构变形值放大了15倍)。考虑到数值模型节点的约束，竖向位移以90°与270°位置为参考点，水平位移以0°与180°位置为参考点。从图4可以得出如下结论。

(1)采用2种模型模拟得到的结构变形的轮廓形状不同，采用梁—弹簧模型时水平位移最大值发生在73°与287°位置，且轮廓线在纵缝接头位置出现了明显的折角；采用修正均质圆环模型时水平位移最大值发生在90°与270°位置，且轮廓线非常平顺。这是由对管片纵缝接头处理方式的不同导致的。

(2)采用2种模型模拟得到的结构水平与竖向收敛变形非常接近。由此说明，本文提出的根据管片纵缝接头刚度k计算盾构隧道横向刚度有效率η的方法是可行的，而且更加简单，计算公式及计算原理更加明晰。

图4　不同加载工况下管片环的变形(单位：mm)

3　横向刚度有效率影响因素分析

由式(14)可知影响横向刚度有效率的因素有：管片环的外径D1(L=[D1-(h/2)]π，D2=D1-h)、管片环分块数量n、管片纵缝接头刚度ki、管片横截面刚度I(包括管片宽度b、管片厚度h)和混凝土弹性模量E。仍以上海通缝拼装盾构隧道为例，拼装管片环的各纵缝接头刚度取为加载工况1对应的纵缝接头刚度，即k1=3.4×107N·m·rad-1，k2=2.8×107N·m·rad-1，k3=5×107N·m·rad-1，则单位弯矩作用下接头转角之和为8.512 6×10-8rad。D1=6.2 m，D2=5.5 m，n=6，h=0.35，E=35.5 GPa，I=4.287 5×10-3m4。采用式(14)分别计算单一因素变化对盾构隧道横向刚度有效率的影响，结果如图5—图9所示。 从图5—图9可以看出：管片环的直径越大，盾构隧道的横向刚度有效率越大；管片截面的抗弯刚度越大、管片纵缝接头刚度越小、管片环分块数量越多，盾构隧道的横向刚度有效率越小。

在此需要指出的是，图5—图9中仅考虑了单一参数的改变对横向刚度有效率的影响，而在实际中，当单一参数改变时，有的不影响其他参数，如增大管片环直径，可以近似认为k不变，则可直接采用式(14)；有的则可能对k有不同程度的影响，从而导致单位弯矩作用下接头转角之和受到影响，如增大管片厚度时，则需要通过足尺试验或理论计算，分析管片接头受力，在得到接头刚度k后，再采用式(14)计算η。

图5　管片环外径对横向刚度有效率的影响

图6单位弯矩作用下接头转角之和对横向刚度有效率的影响

图7　管片厚度对横向刚度有效率的影响

图8　管片宽度对横向刚度有效率的影响

图9　混凝土弹性模量对横向刚度有效率的影响

从横向刚度有效率η的计算公式推导过程可知，影响盾构隧道横向刚度有效率的因素包括梁结构的弯曲变形和纵缝接头位置的转动变形，也即管片环横向总变形是由两部分所导致的，一是由梁结构的弯曲变形所导致的管片环横向变形，二是由纵缝接头的转动变形所导致的管片环横向变形。当管片环的直径增大时，梁结构弯曲变形增大，隧道横向刚度有效率增大，如图5所示；当管片纵缝接头刚度减小时，则盾构隧道横向刚度有效率减小，如图6所示；当管片截面的抗弯刚度EI增大时，管片环梁结构弯曲变形减小，则盾构隧道横向刚度有效率减小，如图7—图9所示。因此，盾构隧道横向刚度有效率不但表征纵缝接头对盾构隧道横向刚度的削弱程度，也反映纵缝接头的转动变形所导致的管片环横向变形占管片环横向总变形的比例，此比例越大，盾构隧道横向刚度有效率越小，反之亦然。

4　结　论

(1)根据盾构隧道横向刚度有效率的定义，推导得到根据管片纵缝接头刚度计算通缝拼装盾构隧道横向刚度有效率η的解析计算公式，并以上海地铁盾构隧道拼装环管为例，验证了计算公式的可行性。

(2)通过反演分析结果可知：盾构隧道的横向刚度有效率与隧道所处地层的土体力学性能和隧道埋深有关，实际是在不同地层土体力学性能、不同隧道埋深状态下，隧道周围土压力不同使得管片纵缝接头刚度不同，从而导致盾构隧道横向刚度有效率不同。

(3)利用刚度有效率η的解析计算公式分析多个单因素对横向刚度有效率影响的结果表明：管片环的直径越大，盾构隧道的横向刚度有效率越大；管片截面的抗弯刚度EI越大、管片纵缝接头刚度越小、管片环分块数量越多，盾构隧道的横向刚度有效率越小。

(4)盾构隧道横向刚度有效率η既表征管片纵缝接头对隧道横向变形刚度的削弱程度，也反映纵缝接头的转动变形所导致的管片环变形占管片环总变形的比例，此比例越大，盾构隧道横向刚度有效率越小；反之亦然。

[1]张鹏. 地铁盾构隧道管片接头的理论分析与应用研究 [D]. 北京：北京交通大学，2011.

(ZHANG Peng. Research on the Theoretical Analysis and Application of the Metro Shield Tunnel Segment Joint[D]. Beijing： Beijing Jiaotong University，2011. in Chinese)

[2]黄大维，周顺华，王秀志，等. 模型盾构隧道管片纵缝接头设计方法[J]. 岩土工程学报，2015，37(6)：1068-1076.

(HUANG Dawei，ZHOU Shunhua，WANG Xiuzhi， et al. Design Method for Longitudinal Segment Joints of Shield Tunnel Model[J]. Chinese Journal of Geotechnical Engineering，2015, 37(6): 1068-1076. in Chinese)

[3]张厚美, 过迟, 付德明. 圆形隧道装配式衬砌接头刚度模型研究[J]. 岩土工程学报, 2000, 22(3): 309-313.

(ZHANG Houmei, GUO Chi, FU Deming. A Study on the Stiffness Model of Circular Tunnel Prefabricated Lining[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(3): 309-313. in Chinese)

[4]朱合华，崔茂玉，杨金松. 盾构衬砌管片的设计模型与荷载分布的研究[J]. 岩土工程学报，2000，22(2)：190-194.

(ZHU Hehua，CUI Maoyu，YANG Jinsong. Design Model for Shield Lining Segments and Distribution of Load[J]. Chinese Journal of Geotechnical Engineering，2000，22(2)：190-194. in Chinese)

[5]蒋洪胜，侯学渊. 盾构法隧道管片接头转动刚度的理论研究[J]. 岩石力学与工程学报，2004，23(9)：1574-1577.

(JIANG Hongsheng，HOU Xueyuan. Theoretical Study of Rotating Stiffness of Joint in Shield Tunnel Segments[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(9)：1574-1577.in Chinese)

[6]钟小春, 朱伟, 秦建设. 盾构隧道衬砌管片通缝与错缝的比较分析[J]. 岩土工程学报, 2003, 25(1): 109-112.

(ZHONG Xiaochun, ZHU Wei, QIN Jianshe. The Comparison of Shield Tunnel with Segment Seams in Sequence and in Stagger[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(1): 109-112. in Chinese)

[7]KOYAMA Y, NISHIMURA T. Design of Lining Segment of Shield Tunnel Using a Beam-Spring Model[J]. Quarterly Report of RTRI, 1998, 39(1): 23-27.

[8]侯公羽，杨悦，刘波. 盾构管片接头模型的改进及管片内力的数值计算[J]. 岩石力学与工程学报，2007，26(增2)：4284-4291.

(HOU Gongyu, YANG Yue, LIU Bo. Improved Joint Model of Shield Tunnel Segments and Numerical Calculation of Inner Forces[J]. Chinese Journal of Rock Mechanics and Engineering, 2007，26(Supplement 2)：4284-4291. in Chinese)

[9]NGOC-Anh Do, DANIEL Dias, PIERPAOLO Oreste, et al. The Behaviour of the Segmental Tunnel Lining Studied by the Hyperstatic Reaction Method[J]. European Journal of Environmental and Civil Engineering, 2014,18(4):489-510.

[10]葛世平，谢东武，丁文其，等. 盾构管片接头简化数值模拟方法[J]. 岩土工程学报，2013, 35(9): 1600-1605.

(GE Shiping, XIE Dongwu, DING Wenqi, et al. Simplified Numerical Simulation Method for Segment Joints of Shield Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(9): 1600-1605. in Chinese)

[11]LEE K M，HOU X Y，GE X W，et al. An Analytical Solution for a Jointed Shield-Driven Tunnel Lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(4): 365-390.

[12]封坤, 何川, 夏松林. 大断面盾构隧道结构横向刚度有效率的原型试验研究[J]. 岩土工程学报, 2011, 33(11):1750-1758.

(FENG Kun, HE Chuan, XIA Songlin. Prototype Tests on Effective Bending Rigidity Ratios of Segmental Lining Structure for Shield Tunnel with Large Cross-Section [J].Chinese Journal of Geotechnical Engineering, 2011, 33(11):1750-1758. in Chinese)

[13]曾东洋，何川. 地铁盾构隧道管片接头刚度影响因素研究[J]. 铁道学报，2005，27(4)：90-95.

(ZENG Dongyang, HE Chuan. Study on Factors Influential in Metro Shield Tunnel Segment Joint Bending Stiffness[J]. Journal of the China Railway Society，2005，27(4)：90-95. in Chinese)

[14]彭益成，丁文其，闫治国，等. 修正惯用法中弯曲刚度有效率的影响因素分析及计算方法[J].岩土工程学报，2013，35(增1)：495-500.

(PENG Yicheng, DING Wenqi, YAN Zhiguo, et al. Analysis and Calculation Method of Effective Bending Rigidity Ratio in Modified Routine Method[J]. Chinese Journal of Geotechnical Engineering，2013，35(Supplement 1): 495-500. in Chinese)

[15]YUKINORI Koyama. Present Status and Technology of Shield Tunneling Method in Japan[J]. Tunneling and Underground Space Technology, 2003(18): 145-159.

[16]黄宏伟，徐凌，严佳梁，等. 盾构隧道横向刚度有效率研究[J]. 岩土工程学报，2006，28(1)：11-18.

(HUANG Hongwei, XU Ling, YAN Jialiang, et al. Study on Transverse Effective Rigidity Ratio of Shield Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 11-18. in Chinese)

[17]YE Fei, GOU Changfer, SUN Haidong, et al. Model Test Study on Effective Ratio of Segment Bending Rigidity of Shield Tunnel[J]. Tunneling and Underground Space Technology, 2014(41)：193-205.

[18]刘建航，侯学渊. 盾构法隧道[M]. 北京：中国铁道出版社，1991.

(LIU Jianhang, HOU Xueyuan, Shield-Driven Tunnels[M]. Beijing: China Railway Publishing House，1991. in Chinese)

[19]鲁亮，孙越峰，柳献，等. 地铁盾构隧道足尺整环结构极限承载能力试验研究[J]. 结构工程师，2012，28(6)：134-139.

(LU Liang, SUN Yuefeng, LIU Xian, et al. Full-Ring Experimental Study on the Ultimate Bearing Capacity of the Lining Structure of the Metro Shield Tunnel[J]. Structure Engineers，2012，28(6)：134-139.in Chinese)