铁路隧道横通道临界风速研究

姜学鹏，张剑高，何　超，王　洁

(1.武汉科技大学 资源与环境工程学院，湖北 武汉　430081；2.武汉科技大学 消防安全技术研究所，湖北 武汉　430081)

横通道是指2条单线铁路隧道之间设置的互为连通、用来疏散旅客的通道。当铁路隧道发生火灾时，人员经横通道疏散至非事故隧道避难[1]。为保证疏散安全，需对横通道进行送风防烟，其中恰好能抑制烟气侵入横通道的风速称为横通道的临界风速[2]。

部分学者对隧道横通道临界风速进行了研究。Tarada[2-3]建议韩国Young Don铁路隧道中横通道门洞处的风速至少为2 m·s-1，认为横通道临界风速与隧道纵向风速、横通道防火门尺寸有关，并基于临界Froude数为4.5的思路提出了计算横通道临界风速的方法；Li[4]通过1/20的缩尺寸模型试验建立了以隧道高度为隧道断面特征尺寸的横通道临界风速计算公式。上述研究均默认横通道垂直于隧道，且均考虑隧道无列车停驶情况，而忽略横通道与隧道夹角及列车阻塞对横通道临界风速的影响，将隧道高度作为特征尺寸仅适用于矩形隧道，不具有普适性。

本文针对铁路隧道列车火灾，根据π定理，推导无量纲横通道临界风速与隧道纵向风速、火源热释放速率、横通道防火门的高度及宽度、横通道与隧道夹角这5个影响参数的量纲关系式。采用数值模拟方法研究这5个影响参数与横通道临界风速之间的量化关系，进而提出以隧道水利直径为特征尺寸的铁路隧道横通道临界风速的无量纲计算公式。

1　横通道临界风速的量纲分析

影响铁路横通道临界风速vcc的因素有[5-6]：隧道纵向风速vt、火灾热释放率Q、空气密度ρ0、空气定压比热cp、空气温度T0、重力加速度g、隧道水利直径HD、横通道防火门的高度Hb及宽度W、横通道与隧道夹角θ。铁路隧道及横通道的坡度[7]一般不超过3%，故忽略坡度的影响，则可列出如下关系式为

f(vcc,Q,vt,ρ0,cp,T0,g,HD,Hb,W,θ)=0

(1)

[M]，[t]，[L]，[T]为4个基本量纲，上述11个物理量均可由该基本量纲表示，式(1)所对应的量纲公式为

f(Lt-1,ML2t-3,Lt-1,ML-3,T,L2t-2T-1,

Lt-2,L,L,L,1)=0

(2)

选取HD，vt，ρ0，T0为基本物理量，根据π定理[8]，式(1)可变为

f(π1,π2,π3,π4,π5,π6,π7)=0

(3)

其中，

通过量纲方程求解可得下列7个无量纲项，分别为

(4)

则式(3)可变为

(5)

根据相似理论的规则，式(6)可变为

(6)

则式(6)可化为

(7)

θ*=θ

将式(7)写成函数形式，则得

(8)

式中：k1，k2，k3，k4，k5和k6均为系数。

2　数值建模及网格敏感性分析

2.1　数值模型及相关参数

以拱形断面隧道为例建立数值模型，采用FDS(Fire Dynamics Simulator)软件进行仿真模拟。隧道模型的长×宽×高为700.0 m×7.0 m×7.5 m，如图1所示；隧道横通道与隧道的夹角为90°；在横通道入口2.0 m处设有矩形防火门，防火门的宽×高为3.0 m×3.0 m；火源热释放率为20 MW，火源位于整列列车纵向中心点的车厢底部，距横通道20.0 m处；横通道的断面尺寸等效为与防火门相同的断面尺寸；隧道的纵向风速为1 m·s-1；列车模型的长×宽×高为213.0 m×3.0 m×3.5 m。

图1　隧道模型示意图(单位：m)

2.2　网格敏感性分析

网格尺寸直接影响着FDS计算的精度和效率。文献[9]研究表明，在火灾特征直径D*≤0.1 m的情况下，FDS能够对火灾烟气流动做出较精确的模拟；文献[10]研究认为，火源区对于网格密度最为敏感，加密火源区可以在控制计算时间的同时有效提高计算精度。火灾特征直径D*的计算公式为[11]

(9)

将火源至横通道附近区域视为重点关注区域，其余区域则为非重点关注区域；将重点关注区域的网格比非重点区域的网格加密1倍，由此建立的隧道模型的三维网格图，如图2所示。为了确定最佳的网格尺寸，取5种不同的网格尺寸作为5种工况(见表1)，分别模拟计算不同工况下防火门门前1 m处竖向空间的温度分布，结果如图3所示。由图3可见：随着网格的加密，模拟计算结果之间的差异越来越小，当重点区域网格尺寸加密至0.067D*时，模拟结果已经与0.005D*时的基本一致。同时，考虑到网格越密，需要的模拟计算时间就越长，因此，综合考虑精度和效率，选取重点区域的网格尺寸为0.067D*，非重点区域的网格尺寸为0.133D*。

图2　隧道模型的三维网格图

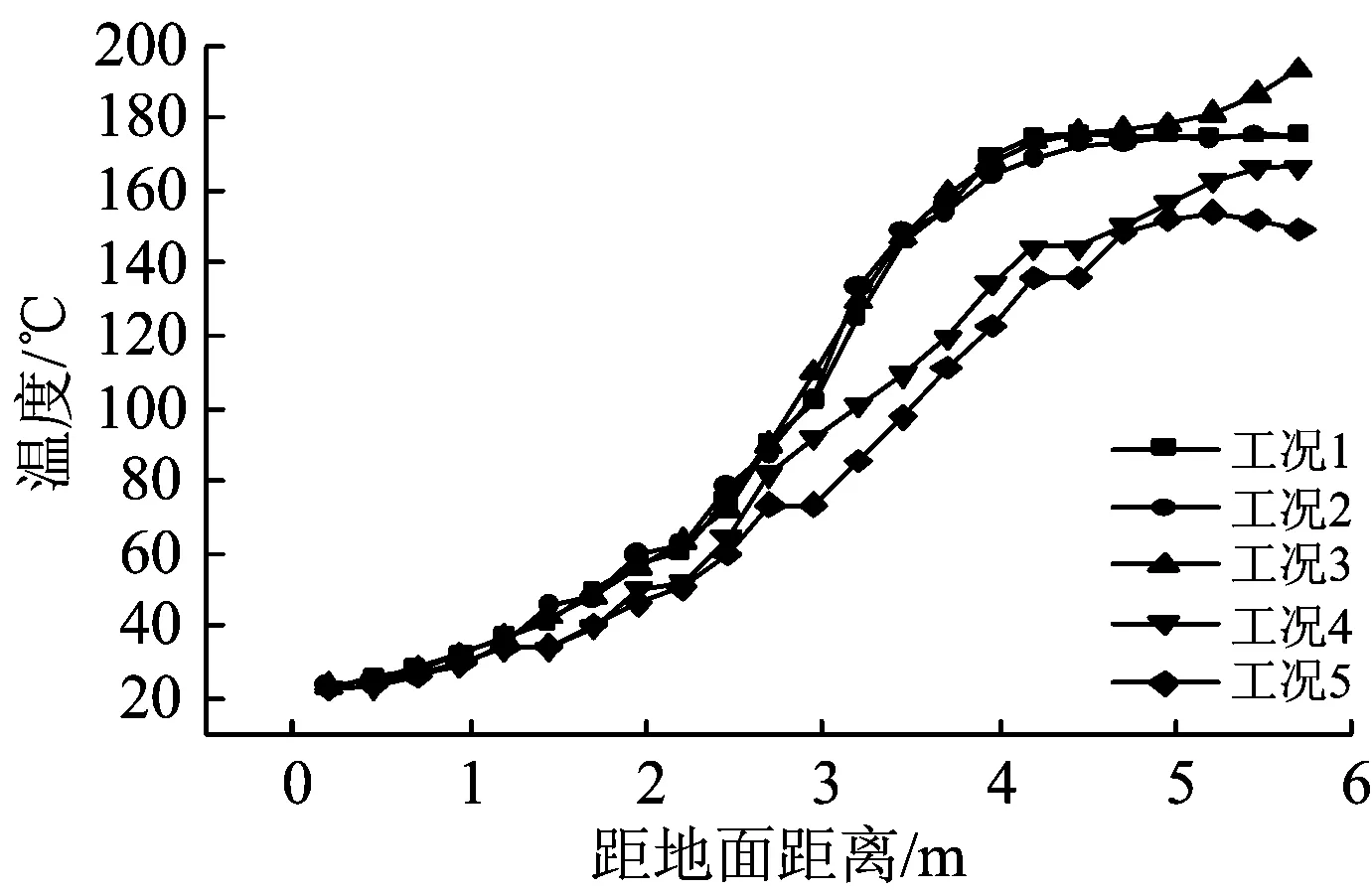
图3　防火门附近竖向温度分布

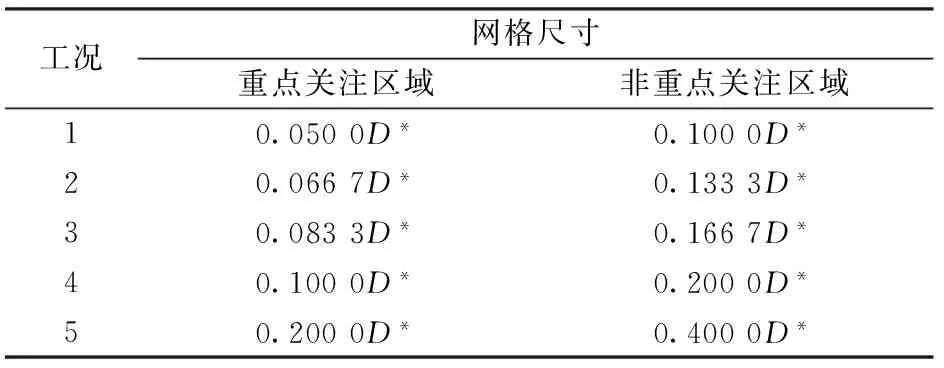
工况网格尺寸重点关注区域非重点关注区域10.0500D*0.1000D*20.0667D*0.1333D*30.0833D*0.1667D*40.1000D*0.2000D*50.2000D*0.4000D*

采用该网格模型和网格尺寸，针对文献[4]中的试验条件数值模拟计算横通道临界风速，并将该模拟值与文献[4]的试验值进行对比，结果见表2，以验证该网格尺寸的合理性。由表2可知：试验值与模拟值的误差在1.69%～5.53%之间，模拟结果与试验结果吻合较好，表明设置的该网格尺寸适用于横通道临界风速的模拟计算，且有较高的可靠性。因此，确定采用该网格尺寸进行数值模拟。

表2　数值模拟计算结果与试验结果[4]对比

2.3　横通道临界风速确定方法

采用直接观测法和逆流长度外推法综合判定横通道临界风速。直接观测法：根据模拟时横通道内烟气的蔓延情况，首先以0.1 m·s-1的风速间隔不断加大横通道送风风速v2，当烟气逆流长度接近0 m时再以0.01 m·s-1的风速间隔不断加大风速v2，直至肉眼观察烟气恰好不侵入防火门，将此时的送风风速v2确定为横通道临界风速，具体操作步骤如图4所示。逆流长度外推法：通过横通道顶板设置的温度测点获得顶板处温度分布情况，以得到横通道内烟气的逆流长度，根据逆流长度外推可得逆流长度为0 m时的横通道送风风速v2，即

图4　直接观测法

横通道临界风速，逆流长度外推法如图5所示。为减小模拟计算的误差，横通道临界风速取以上2种方法所得结果的平均值。

图5　逆流长度外推法

3　数值模拟结果与分析

3.1　隧道纵向风速vt的影响

图6　无量纲隧道纵向风速与无量纲横通道临界风速的关系

3.2　火源热释放率Q的影响

在隧道纵向风速为1.0和1.5 m·s-1时，不同无量纲火源热释放率对无量纲横通道临界风速影响的模拟结果如图7所示。由图7可知：随着火源热释放率的增大，横通道临界风速逐渐增大；2条拟合曲线均为1/3次方增长曲线，相关系数分别为0.999 5和0.998 6，表明拟合曲线函数具有很好的可靠性。这是因为在不改变火源位置及隧道纵向风速的情况下，火源热释放率越大，横通道防火门处的热压也越大，即所需临界风速也越大。由此可得：k3=1/3。

图7　无量纲火源热释放率与无量纲横通道临界风速的关系

3.3　防火门高度Hb的影响

图8　无量纲防火门高度与无量纲横通道临界风速的关系

3.4　防火门宽度W的影响

在火源热释放率为10和20 MW时，不同防火门宽度对横通道临界风速影响的模拟结果如图9所示。由图9可得：无量纲横通道临界风速不随无量纲防火门宽度的变化而变化。这是因为烟气侵入横通道的驱动力主要是烟气的热压和动压，在横通道与隧道夹角及其他因素一定的情况下，动压也为一定值，而门宽的改变基本不会使防火门附近的热压产生改变，即门宽对横通道临界风速基本无影响。由此可得：k5=0。

图9　无量纲防火门宽度与无量纲横通道临界风速的关系

3.5　横通道与隧道夹角θ的影响

在火源热释放率为10和20 MW时，横通道与隧道不同夹角对横通道临界风速影响的模拟结果如图10所示。由图10可知：随着横通道与隧道夹角的增加，临界风速逐渐减小；2条拟合曲线均为-3/8次方曲线，其相关系数分别为0.990 3和0.987 8。这是由于随着夹角的增大，烟气侵入横通道的动压不断减小，从而导致抑制烟气侵入的风速也会随之减小，即横通道临界风速变小。由此可得：k6=-3/8。

图10　无量纲夹角与无量纲横通道临界风速的关系

3.6　量纲公式的确定

根据上述分析可知，k2，k3，k4，k5，k6分别为3/7(或-3/40)，1/3，7/10，0，-3/8。则式(8)可转化为

(10)

(11)

图11　横通道临界风速模拟结果

3.7　公式对比

为验证式(11)的可靠性，在参照本文计算参数和模型设置的前提下，仅改变火源热释放率或防火门高度，将式(11)的计算结果、Li公式的计算结果[4]和数值模拟结果均列于图12中。由图12可知：式(11)的计算结果与数值模拟结果一致，而Li公式的计算结果较式(11)预测的结果偏小。这主要是由于：列车的阻塞作用，使得烟气层的厚度增大，横通道防火门处的热压也相对变大，从而需要更大的临界风速来抑制烟气侵入横通道；Li公式选用隧道高度作为特征尺寸，在用于一般拱形隧道横通道临界风速的预测时，使得预测值偏小；Li的试验模型为复合结构(内衬钢板，外覆混凝土)，在实验过程中会存在一定的热损失，而相较于数值模拟中设置为绝热材料的隧道、列车，在防火门处烟气的热压相对减小，导致Li公式的预测值较小。

图12　模型结果与公式对比

4　结　论

(1)横通道临界风速随隧道纵向风速的增大呈现3/7次方增长关系，但当纵向风速超过0.114时，横通道临界风速随纵向风速的增大而减小，与其呈现-3/40次方关系；同时，横通道临界风速与火源热释放率呈现1/3次方关系与横通道防火门的高度近似成6/5次方关系，与宽度无关，与横通道及隧道之间的夹角成-3/8次方关系。

(2)明确了铁路隧道列车火灾时横通道无量纲临界风速与5个无量纲参数之间的关系，建立了以隧道水利直径为隧道特征长度的无量纲横通道临界风速计算公式，为横通道防烟风速的确定提供理论支持。

[1]李琦,王明年,于丽. 长大铁路隧道火灾模式下人员疏散试验研究[J]. 中国铁道科学, 2015,36(6):78-84.

(LI Qi, WANG Mingnian, YU Li. Experimental Study on Evacuation under Fire Mode in Long and Large Railway Tunnel[J]. China Railway Science, 2015,36(6):78-84. in Chinese)

[2]TARADA F. Critical Velocities for Smoke Control in Tunnel Cross-Passages[C]//Proceedings of the First International Conference on Major Tunnel and Infrastructure Projects. Taiwan: ITC, 2000: 22-24.

[3]TARADA F, BOPP R, NYFELER S, et al. Ventilation and Risk Control of the Young Dong Rail Tunnel in Korea[C]//International Conference on Major Tunnel and Infrastructure Project. Taiwan: ITC, 2000: 22-24.

[4]LI Y Z, LEI B, INGASON H. Theoretical and Experimental Study of Critical Velocity for Smoke Control in a Tunnel Cross-Passage[J]. Fire Technology, 2013, 49(2): 435-449.

[5]李颖臻,雷波. 隧道间联络通道临界风速模型[J]. 铁道学报,2008,30(3):87-90.

(LI Yingzhen, LEI Bo. Model of Critical Velocity in a Tunnel Cross-Passage[J]. Journal of the China Railway Society, 2008,30(3):87-90.in Chinese)

[6]姜学鹏,张剑高,丁玉洁. 隧道阻塞比对临界风速影响的模型试验研究[J]. 中国铁道科学, 2015,36(4):80-86.

(JIANG Xuepeng, ZHANG Jiangao, DING Yujie. Model Test Study on Effect of Blockage Ratio on Critical Wind Velocity in Tunnel[J]. China Railway Science, 2015,36(4):80-86. in Chinese)

[7]易思蓉,聂良涛,陈彦恒. 电气化铁路隧道最大坡度系数研究[J]. 中国铁道科学,2013,34(6):42-48.

(YI Sirong, NIE Liangtao, CHEN Yanheng. Research on the Maximum Gradient Coefficient of Electrified Railway Tunnel[J]. China Railway Science, 2013, 34(6):42-48. in Chinese)

[8]毛军,郗艳红,杨国伟. 列车编成辆数对高速列车横风气动特性影响的数值分析[J]. 中国铁道科学, 2012,33(1):78-85.

(MAO Jun, XI Yanhong, YANG Guowei. Numerical Analysis on the Influence of Train Formation on the Aerodynamic Characteristics of High-Speed Trains under Crosswind[J]. China Railway Science, 2012,33(1):78-85. in Chinese)

[9]WENG M C, LU X L, LIU F, et al. Study on the Critical Velocity in a Sloping Tunnel Fire under Longitudinal Ventilation[J]. Applied Thermal Engineering, 2016, 94: 422-434.

[10]祝实,霍然,胡隆华,等. 网格划分及开口处计算区域延展对FDS模拟结果的影响[J]. 安全与环境学报,2008,8(4):131-135.

(ZHU Shi, HUO Ran, HU Longhua, et al. Influence of Mesh Grid and Computational Domain on FDS Simulation[J]. Journal of Safety and Environment, 2008,8(4):131-135. in Chinese)

[11]LIN C J, CHUAH Y K. A Study on Long Tunnel Smoke Extraction Strategies by Numerical Simulation[J]. Tunnelling and Underground Space Technology, 2008, 23(5): 522-530.