基于活塞效应的隧道埋深对地铁车站通风换气性能的影响

陈　超，李小娜，李　琼，袁浩庭，王陆瑶，李亚茹

(1.北京工业大学 建筑工程学院，北京　100124；2.北京工业大学 绿色建筑环境与节能技术北京市重点实验室，北京　100124)

随着城市地铁的迅速发展，地铁环境问题已经愈来愈引起人们的关注[1-2]。地铁列车在区间隧道内高速行进过程中产生活塞效应，从而带动区间隧道和车站内空气流动，并通过车站出入口、风井与外界进行通风换气[3]。如果对活塞效应加以有效利用，将对地铁车站空气环境改善起到积极作用。

基于活塞效应对地铁车站空气环境改善的积极作用，国内外学者做了许多相关的研究。杨晖[4]通过计算分析列车进出站过程中车站各区域空气的流速变化和流场分布，提出活塞效应的有效利用不仅可以减少乘客的不舒适感、改善车站内的空气质量，而且对地铁节能有积极作用。孙云雷等[5]关于活塞风与空调送风共同作用下地铁车站的气流耦合模型试验结果表明，活塞风对地铁车站内空气环境的影响起主导作用。Peng Xue[6]通过CFD模拟分析，认为活塞风在各流动通道以特定的流出和吸入比流动，列车进站端风井比出站端风井对活塞风的影响更大。T. Moreno[7]通过对巴塞罗那市地铁车站的空气质量(PM, CO2和CO)进行高精度监测，发现单轨道的站台结构主要依赖强制隧道通风减少车站的PM浓度，而双轨道站台结构仅依赖活塞效应即可维持车站内稳定的PM浓度。杨伟超等[8]采用室内污染物浓度演化单箱物理模型建立了地铁空气污染物控制方程，对站台和区间隧道的CO2浓度变化特性进行了分析与评价。 Zhang Lin等[9]采用CFD模拟软件针对地铁车站换乘站内的CO和CO2浓度以及地铁车站的通风效果进行分析，提出了1种可改善室内空气品质和热舒适性的通风模式。Chi-Ji Lin等[10]针对地铁环控系统中开式系统活塞效应的影响因素进行了实测和模拟研究，指出在考虑利用活塞效应进行隧道通风时，通风井的长度是很重要的参数。Pope[11]等通过分析地铁系统中影响通风的因素和空气温度后发现，当通风井的截面积为20 m2时，活塞风的空气流动及地铁车站的空气温度是令人满意的。Zhao Yang[12]等人提出1种新型的地铁环境控制系统，通过CFD模拟方法，分析了该控制系统下活塞风对车站舒适性及其节能效果的影响，并指出在不同城市应用该系统时节能效果不同。这些研究成果表明，活塞风对地铁车站及隧道通风换气有积极作用，而活塞风流动特性会受到列车运行速度、隧道结构(隧道长度及截面尺寸)、风井设置模式及尺寸等因素的影响[13]。但是关于隧道埋深对地铁活塞效应及地铁车站通风换气性能影响的研究还较少。

本文以北京地铁4号线灵境胡同车站及其两侧的区间为例，针对单风井设置模式[14]，根据所构建的隧道通风性能评价指标，采用计算流体力学软件FLUENT 15.0[15]计算不同隧道埋深处地铁车站及区间隧道各断面空气流动的压力场和速度场，研究隧道埋深、风井横截面积对地铁车站通风换气性能的影响规律，以期为地铁系统活塞效应的有效利用提供设计依据和参考。

1　地铁车站及区间隧道空气流动压力场和速度场的数值模拟

1.1　计算车站及其区间隧道的几何结构及尺寸

灵境胡同车站为双层岛式车站，如图1所示。站台的长×宽×高为130 m×20 m×4.85 m；站台两端设有楼梯通向站厅，站厅的长×宽×高为90 m×20 m×3.3 m；站厅设有CB，CC和CD共3个地面出入口通道(简称通道)通向室外地面，CB通道横截面的宽×高为6.0 m×2.5 m, CC和CD通道横截面的宽×高均为4.5 m×2.5 m。

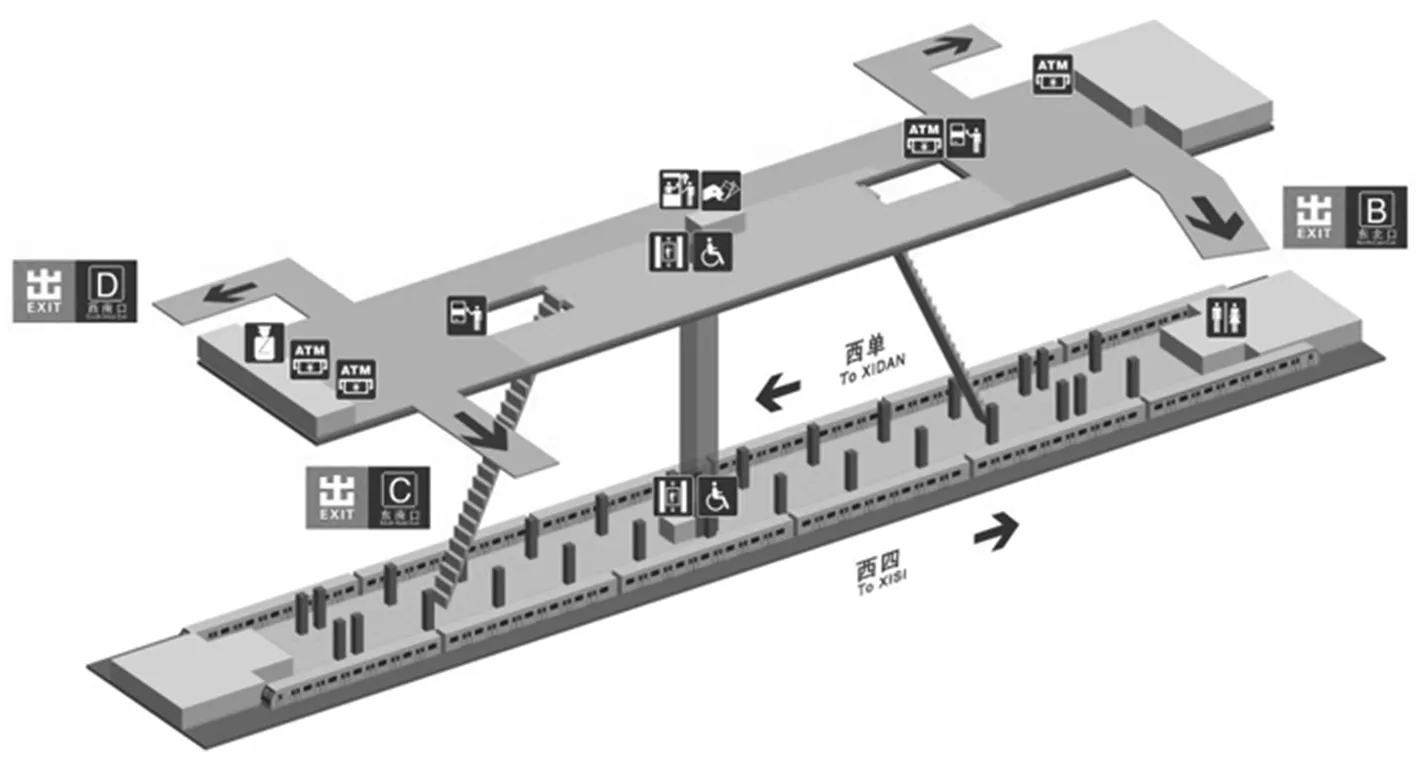
图1　灵境胡同车站构造示意图

图2为该计算车站及其连接区间隧道的示意图。车站左侧区间隧道长982 m，隧道内净空的宽×高为4.4 m×4.6 m；车站右侧区间隧道长879 m，隧道内净空的宽×高为4.4 m×4.6 m。车站两端各设置1个风井，位置分别在距离车站站台进站端100 m的区间隧道内(简称为风井VSA和风井VSB)，风井横截面面积均为16 m2。

图2　灵境胡同车站及其区间隧道相对位置示意图(单位：m)

1.2　数值建模及网格划分

采用Gambit软件建立计算车站的全尺寸网格模型，如图3所示。区间隧道采用结构型网格划分，网格的长×宽×高为0.5 m×0.4 m×0.4 m；地铁车站内部结构采用非结构性网格划分，并且在气流流动复杂区域进行网格加密处理[16]；模型的总网格数为3.1×106个。

图3　车站及区间网格模型

1.3　边界条件及模型求解

根据列车实际运行过程，应用FLUENT 15.0软件的动网格模型，对列车运行过程中活塞效应随时间的变化规律进行模拟。网格更新采用动态分层方式；区间与站台的交界面采用滑动交界面进行耦合；列车运行速度均按照图4所示实际高峰时段的列车运行速度进行赋值。西单站上行线(西单站→灵境胡同站→西四站)的列车先于西四站下行线(西四站→灵境胡同站→西单站)的列车行驶；自上行线列车起动开始计时，在52 s时上行线列车车头开始经过风井VSB，在56 s时下行线列车车头开始经过风井VSA；在82 s时2列列车均完全停靠在灵境胡同站站台，在112 s时上行线列车驶离灵境胡同站；直至181和191 s时，2列列车均走完全程。

图4　列车运行速度时程曲线

两列车的运行时长分别为181和191 s，考虑到列车停止运行后活塞风会再继续流动一段时间，故将动网格模拟时长设置为200 s。时间步长为0.02 s，每时间步长迭代运算20次，残差收敛标准设为0.001；在t=0时，地铁车站及隧道区间内的相对大气压力及速度均为0；t>0时，车站地面出入口及风井地面出口都为大气压力边界，入口处边界为动网格与静网格耦合Interface面，即动网格区域(隧道)内的空气受活塞压力作用可以通过此面流至静网格区域(风井及站台站厅等)；忽略人员走动对空气流动的影响。

采用k—ε湍流模型计算地铁列车运行过程中产生的活塞效应；采用PISO算法计算瞬态运算中的速度与压力的耦合问题。对流与扩散项的离散采用二阶迎风格式，瞬态运算的时间离散采用一阶隐式[14]。

1.4　模拟计算工况

灵境胡同站的埋深为15 m，风井的横截面面积为16 m2。为分析隧道埋深和风井结构尺寸对地铁活塞效应的影响，在实际隧道埋深及风井横截面积的基础上共设置7种计算工况，见表1。

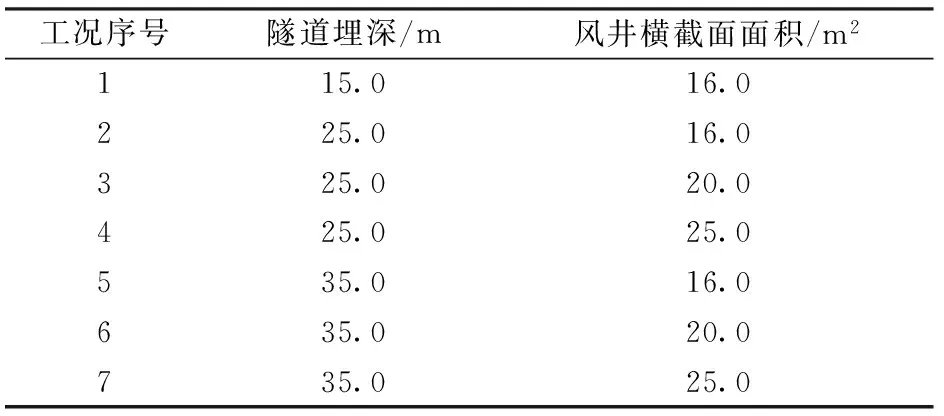
表1　计算工况(Case set)

1.5　模拟计算方法的验证(工况1)

1.5.1车站空气速度分布特性

工况1条件下地铁区间隧道和计算车站各断面(沿列车行驶方向)平均瞬时风速随时间的变化规律如图5所示，图5中正值表示向室外排风，负值表示从室外引入新风。由图5可知：当两列车相向驶向计算车站过程中(0～82 s)，由于上行线的列车先行，上行区间风井VSB处的风速先于其他断面增大，各断面排风速度也随着列车运行速度的增加而增加，在两列车经过风井VSA和VSB时，风井断面风速会出现骤降，这时大部分空气从计算车站站台通过通道向室外排风；当两列车同时停泊在计算车站的站台上时(82～112 s)，各断面仍处于排风状态，这主要是由空气流动的延迟性导致的；在两列车同时驶离车站进入区间隧道过程中，处于排风状态的风井和通道排风的风速骤减为0，然后变为进风状态，室外空气通过风井和通道被引入，直至列车完全停止并延后一定时间(200 s)止，地铁区间隧道及车站各断面的风速才逐渐降低为0。

图5地铁区间隧道和车站各断面平均风速随时间变化的曲线

1.5.2计算方法有效性验证

为了验证应用FLUENT软件的网格模型进行模拟的有效性，仿真模拟通道CB的平均瞬时风速；然后实测通道CB的平均瞬时风速，实测时采用Testo-435型风速仪(量程范围为0～500×10-6m·s-1，精度为±50×10-6m·s-1，分辨率为1×10-6m·s-1)，测点选取通道CB断面中心距地面高度1.5 m处，数据记数频率为1次·s-1；将模拟值与实测值进行比较，结果如图6所示。由图6可知：两者随时间变化的趋势一致，只是实测值稍大于模拟值。出现误差的原因有：一是因为实测过程中人员走动对空气流动的扰动作用；二是因为受现场实测条件限制，实测结果的精准性稍差。由此说明，该模型是正确的、合理的，可以用于模拟分析隧道埋深和风井截面面积对地铁活塞效应的影响。

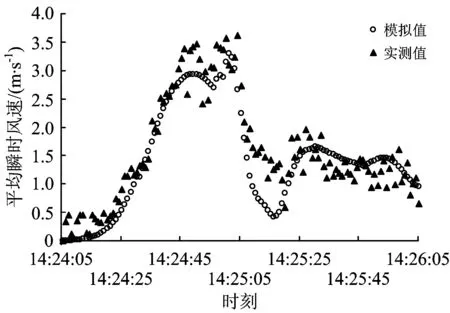
图6　实测断面平均瞬时风速的模拟值与实测值对比

2　地铁车站通风换气性能评价指标

(1)

(2)

(3)

(4)

3　模拟计算结果分析

3.1　隧道埋深对车站通风换气性能的影响

3.1.1隧道埋深与活塞风速

取工况1、工况2和工况5，即只改变隧道埋深，不改变风井的横截面面积，采用上述模拟方法，模拟得到各风井和通道断面的平均瞬时风速随隧道埋深的变化规律分别如图7和图8所示。由图7和图8可知：风井与通道断面的平均瞬时风速随时间的变化规律相同，均随着隧道埋深的增加而降低。

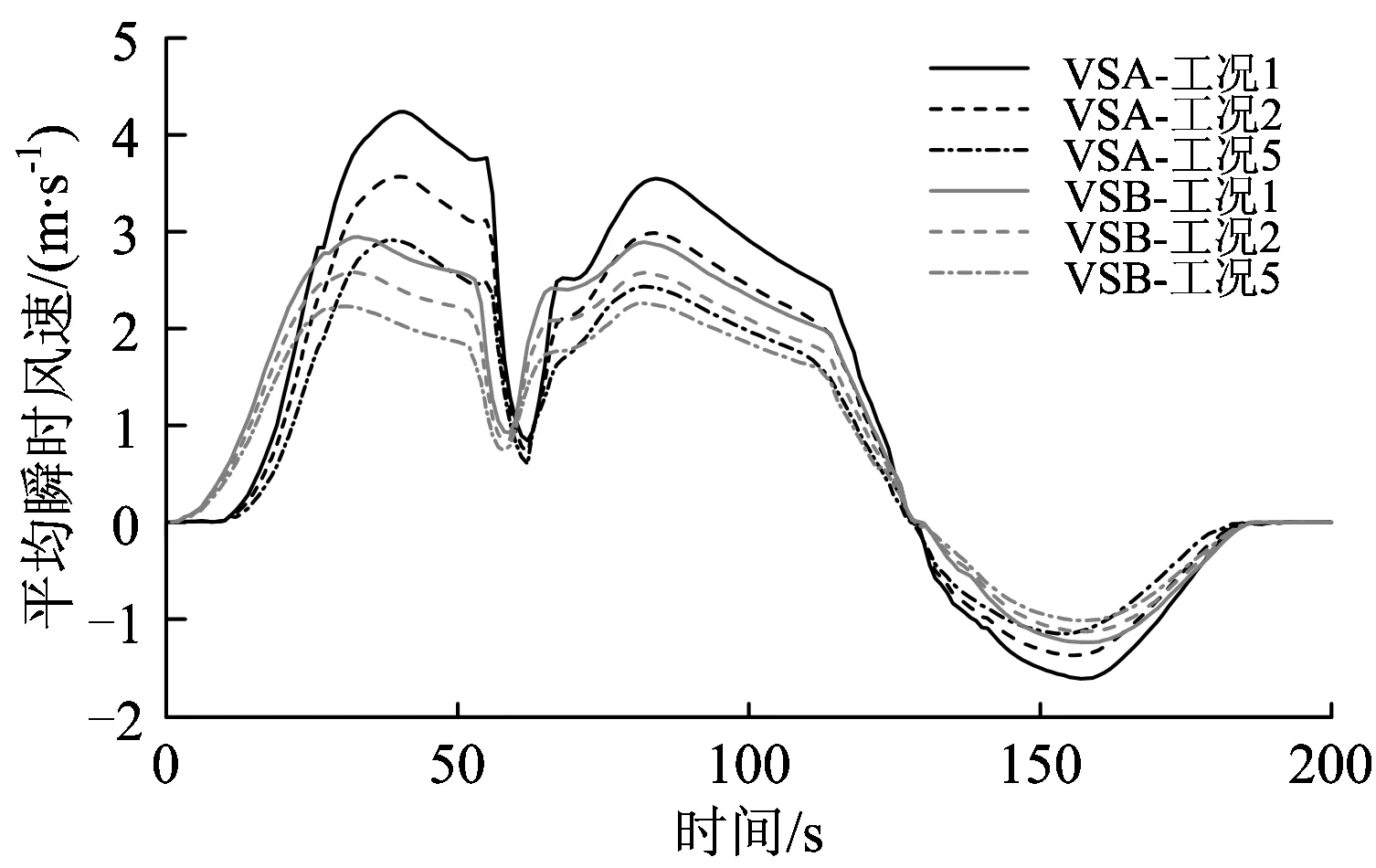
图7不同风井断面平均瞬时风速与隧道埋深的关系曲线

图8　不同通道断面平均瞬时风速与隧道埋深的关系曲线

3.1.2隧道埋深与隧道进/排风量

根据图8和图9所示平均瞬时风速曲线，分别采用式(1)—式(4)计算得到不同隧道埋深时各风井和通道的排风量和进风量，见表2。

表2　不同隧道埋深时风井和通道的通风量(工况1、工况2及工况5)

由表2可知：随着隧道埋深的增加，风井、通道的进风量及排风量，以及总排风量和总进风量均逐渐减少；当隧道埋深由15 m(工况1)增加到35 m(工况5)时，风井的排风量从9 141 m3减少到6 558 m3，减少了28.3%；风井和通道的总进风量从5 222 m3减少到3 834 m3，减少了26.6%，说明活塞风对地铁车站通风换气的积极作用被削弱。

3.2　风井横截面面积对车站通风换气性能的影响

3.2.1风井横截面面积与活塞风速

取工况2、工况3及工况4，即隧道埋深不变，只改变风井的横截面面积；采用上述模拟方法，模拟得到各风井和通道断面的平均瞬时风速随风井横截面面积的变化规律如图9和图10所示。由图9和图10可知，风井横断面的活塞风速由于横截面面积的增加而有所降低，而通道横载面的平均瞬时风速变化不大。

图9不同风井横截面面积时风井断面平均瞬时风速变化曲线

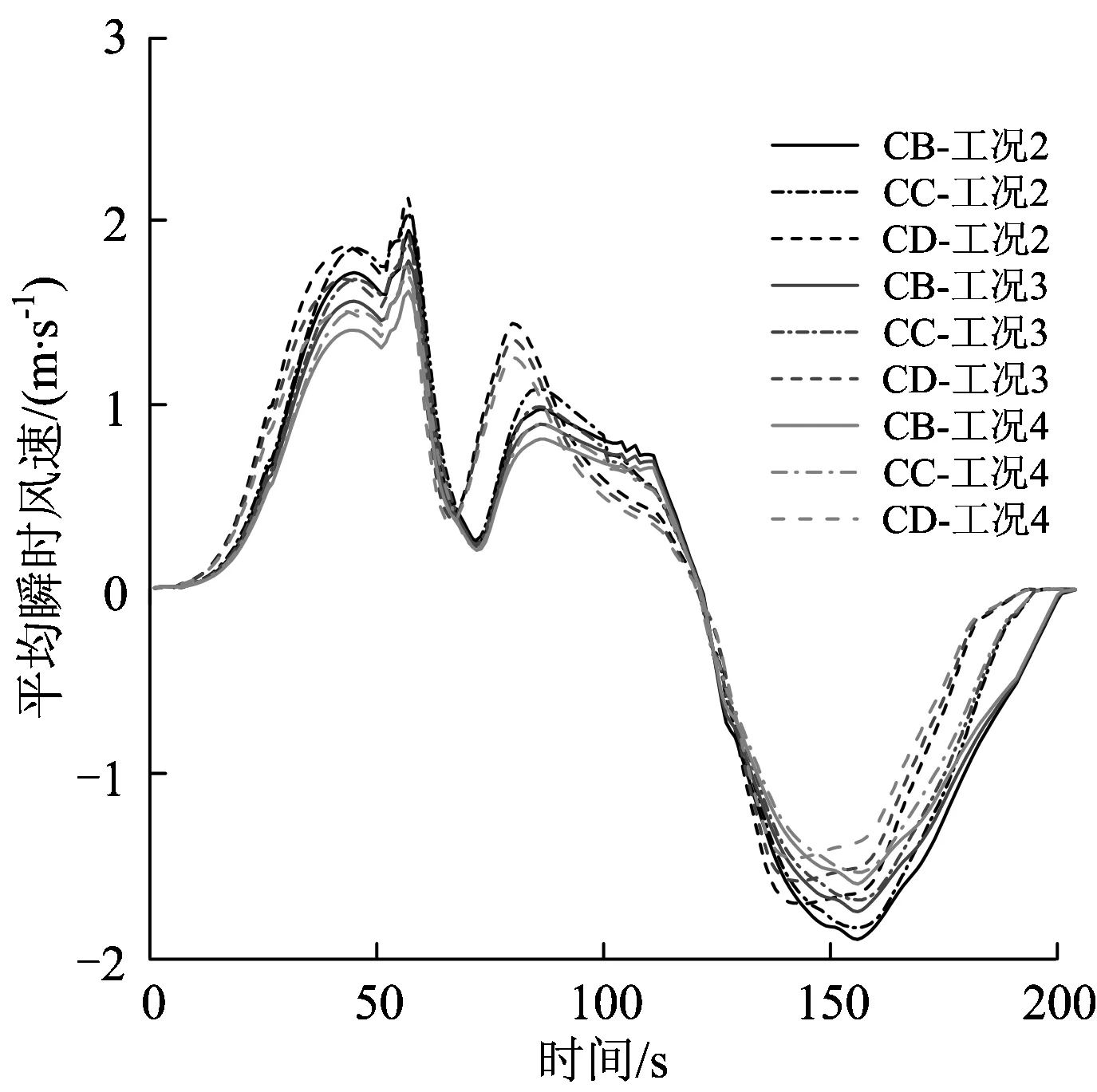
图10不同风井横截面面积时通道平均瞬时风速变化曲线

3.2.2风井横截面面积与隧道进/排风量

根据图9和图10所示平均瞬时风速曲线，分别采用式(1)—式(4)计算得到风井及通道的排风量和进风量，见表3。由表3可知：随着风井横截面面积的增加，风井、通道的进风量和排风量，以及总排风量和总进风量均逐渐增加；当风井横截面积由16 m2(工况2)增加到25 m2(工况4)时，风井的排风量由7 849 m3增加到9 814 m3，增加了25%；风井和通道的总进风量由4 527 m3增加到4 921 m3，增加了8.7%。说明增加风井的横截面面积，对有效利用活塞风改善地铁隧道通风换气性能具有积极作用。

表3　不同风井横截面面积时风井和通道的通风量(工况2、工况3及工况4)

3.3　基于隧道通风性能的隧道埋深—风井横截面面积取值的平衡

由以上分析可知，隧道埋深的增加将直接导致活塞风对地铁隧道通风换气积极作用的削弱，而适当增加风井的横截面面积可有效平衡隧道埋深带来的不利影响。因此，对工况1—工况7，模拟各风井和通道断面处的平均瞬时风速，再根据式(1)—式(4)计算得到各工况下风井的排风量及风井和通道的总进风量，如图11所示。由图11可知：当隧道埋深由15 m分别增加到25和35 m时，如果将风井横截面面积相应地从16 m2增加到20和25 m2(工况1，工况3和工况7)，风井的排风量分别为9 141， 9 005， 8 462 m3；风井和通道的总进风量分别为5 222， 4 745， 4 238 m3。可见，适当增加风井横截面面积，可有效平衡由于隧道埋深增加而引发活塞风对地铁系统通风性能的减弱。

图11　各工况下风井的排风量及风井和通道的总进风量

4　结　论

(1)隧道埋深由15 m增加到35 m，风井的横截面面积不变，则风井的排风量从9 141 m3减少到6 558 m3；风井和通道的总进风量从5 222 m3减少到3 834 m3。说明隧道埋深的增加不利于地铁车站的通风换气。

(2)隧道埋深不变，风井的横截面积由16 m2增加到25 m2，则风井的排风量由7 849 m3增加到9 814 m3；风井和通道的总进风量由4 527 m3增加到4 921 m3。说明增加风井横截面面积，对有效利用活塞风改善地铁车站的通风换气性能具有积极作用。

(3)隧道埋深由15 m分别增加到25和35 m，如果将风井横截面面积从16 m2增加到20和25 m2，则可有效平衡由于隧道埋深增加而引发的活塞风对地铁系统通风性能作用的减弱。

[1]叶晓江，连之伟，蒋淳潇，等. 上海地铁站台环境质量分析[J]. 建筑热能通风空调，2009,28(5):61-63.

(YE Xiaojiang, LIAN Zhiwei, JIANG Chunxiao, et al. Analysis on Environmental Quality in Shanghai Metro Stations[J]. Building Energy & Environment, 2009,28(5):61-63.in Chinese)

[2]王子甲,陈锋,施仲衡. 北京城市轨道交通中远期能耗预测研究[J]. 中国铁道科学, 2013,34(3):133-136.

(WANG Zijia, CHEN Feng, SHI Zhongheng. Prediction on Medium and Long Term Energy Consumption of Urban Rail Transit Network in Beijing[J]. China Railway Science, 2013,34(3):133-136.in Chinese)

[3]陈超，潘嵩，李真真，等. 地铁活塞效应对地面出入口引入新风流动特性的影响[J]. 重庆大学学报，2011,34(增刊)：100-105.

(CHEN Chao, PAN Song, LI Zhenzhen, et al. The Influence of Subway Piston Effect on the Fresh Air Introduced from Entrances[J]. Journal of Chongqing University,2011,34(Supplement):100-105.in Chinese)

[4]杨晖. 地铁列车活塞风对站台空气环境影响的数值模拟[J]. 北京建筑工程学院学报，2007，23(2)：8-13.

(YANG Hui. Numerical Simulation of Piston Wind on Platform Air Environment[J]. Journal of Beijing University of Civil Engineering and Architecture, 2007，23(2)：8-13.in Chinese)

[5]孙云雷，王丽慧. 地铁活塞风与空调送风耦合的温度场的试验研究[J]. 流体机械，2012，40(11)：54-58.

(SUN Yunlei,WANG Lihui. Experimental Study of Temperature Field of the Piston Wind and Air-Conditioning Airflow Coupling[J]. Fluid Machinery,2012, 40(11):54-58.in Chinese)

[6]XUE P, YOU S J, CHAO J Y, et al. Numerical Investigation of Unsteady Airflow in Subway Influenced by Piston Effect Based on Dynamic Mesh[J]. Tunnelling and Underground Space Technology, 2014, 40 (2): 174-181.

[7]MORENO T，PéREZ N，RECHE C，et al. Subway Platform Air Quality: Assessing the Influences of Tunnel Ventilation, Train Piston Effect and Station Design[J]. Atmospheric Environment, 2014, 92: 461-468.

[8]杨伟超, 彭立敏, 艾小冬. 地铁内空气品质的动态变化特性分析[J]. 铁道科学与工程学报，2009，6(6)：54-58.

(YANG Weichao,PENG Limin,AI Xiaodong. Analysis of Dynamic Evolution Characteristics on Air Quality inside Subway[J]. Journal of Railway Science and Engineering，2009,6(6):54-58.in Chinese)

[9]ZHANG Lin, FENG Jiang, T T Chow, et al. CFD Analysis of Ventilation Effectiveness in a Public Transport Interchange[J]. Building and Environment, 2006，41(3)：254-261.

[10]LIN C J,CHUAH Y K,LIU C W. A Study on Underground Tunnel Ventilation for Piston Effects Influenced by Draught Relief Shaft in Subway System[J]. Applied Thermal Engineering，2008,28(5/6)：372-379.

[11]POPE C W,NEWMAN D G, Henson D A. The Factors Affecting Draught Relief and Air Temperature in an Underground Metro System[C]//Tenth International Symposium on Aerodynamics and Ventilation of Vehicle Tunnels. November, Boston, USA：BHRG, Publication，2000：43.

[12]YANG Zhao, SU Xiangchao, MA Feng, et al. An Innovative Environmental Control System of Subway[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147:120-131.

[13]王韦,王建宇,陈正林. 隧道中高速列车活塞风及空气阻力的计算[J].中国铁道科学, 1999，20(1): 9-16.

(WANG Wei, WANG Jianyu, CHEN Zhenglin. Piston Wind of High-Speed Train in Tunnel and Air Resistance Calculation[J]. China Railway Science, 1999，20(1): 9-16.in Chinese)

[14]陈超，严乐，潘嵩，等.基于活塞效应的地铁隧道风井设置优化方法[J].中国铁道科学，2015,36(6): 70-77.

(CHEN Chao,YAN Le,PAN Song, et al.Optimal Setting of Air Shafts for Subway Tunnel Based on Piston Effect[J].China Railway Science，2015,36(6):70-77.in Chinese)

[15]冯炼,刘应清.地铁通风网络的数值分析[J].中国铁道科学, 2002,23(1): 133-135.

(FENG Lian, LIU Yingqing[J]. Numerical Simulation Analysis of Ventilation Network in Subway [J]. China Railway Science, 2002,23(1): 133-135.in Chinese)

[16]MARTA López González, MóNICA Galdo Vega, JESúS Manuel Fernández Oro, et al. Numerical Modeling of the Piston Effect in Longitudinal Ventilation Systems for Subway Tunnels[J]. Tunnelling and Underground Space Technology，2014, 40:22-37.