高寒地区高速铁路桥梁下部结构模态参数的变化规律研究

闫宇智，战家旺，张　楠，夏　禾，强伟亮

(北京交通大学 土木建筑工程学院，北京　100044)

桥梁结构由上部结构和下部结构组成，近年来铁路桥梁健康状态的相关研究主要集中在上部结构，下部结构的研究往往被忽视。桥梁下部结构的工作状态直接影响整个桥梁的安全，若桥墩基础状态不良，即使上部结构状态良好，整个桥梁的使用性能也会受到影响。鉴于此，桥墩健康状况的检测与评估逐渐成为学术界和工程界关注的热点[1]。

自振频率是最容易测量的模态参数，因此基于自振频率的健康状态评判方法被广泛采用[2]。桥墩频率的传统测试方法主要包括结构余振自由衰减振动法[3]和激励模态分析法[4-5]。余振法是目前国内铁路桥梁检定部门最常用的方法，然而该方法采用的振动信号成分较为复杂，很容易造成自振频率的误判，一般仅适用于振动形式较为单一的结构。模态分析法对人力、物力消耗较大，当需要对大量桥墩进行频率测试时具有很大的局限性。战家旺等[6]提出了基于冲击振动试验法的模态参数辨识方法。然而其只适用于桥墩的各阶自振频率相间比较稀疏，墩—梁耦合不强的情况。随着现代桥梁的逐步发展，特别是高速铁路桥梁的出现，墩—梁强耦合现象也逐渐显现出来，这也给桥墩频率的准确识别造成了极大的困难。

高寒地区的气象特点是年温差和昼夜温差均较大，气候条件恶劣。在典型的高寒地区[7]，土体冻融循环和冻胀问题突出，容易导致地基破坏、结构刚度下降、耐久性和承载力不足等服役性能方面的问题，进而引起墩身和基础约束刚度的下降，并表现为桥梁下部结构自振频率等模态参数的变化。

本文针对高寒地区高速铁路多跨简支梁桥墩—梁振动强耦合的特点，采用复合随机子空间模态分析法(简称随机子空间法)和冲击振动试验法相结合的信号处理方法，对桥梁下部结构的模态参数进行识别。并分析了一个冻融循环周期内不同因素对桥墩自振频率的影响规律。

1　桥梁下部结构模态参数识别方法

由于冲击荷载施加简便，且能激起结构较宽频带的响应，因此本文将其作为高速铁路桥梁下部结构模态参数识别的激振力。

结构的模态参数主要包括频率、振型和阻尼比。由于实际结构中阻尼比变化较小，因此暂不对阻尼比进行讨论。

冲击振动试验法是基于频域的模态识别方法，仅需要在墩顶布置1个传感器即可得到结构的自振频率，且可以利用行车间隙进行试验，故相对而言试验比较容易，当对大量桥墩进行频率测试时，该方法具有方便、快捷等优点。

冲击振动试验法的基本原理是用重锤击打桥墩，根据桥梁的振动响应求得其自振频率。由于输入激励相对较小，可以认为体系的响应是线性的。此时，应用振型叠加法可将传递函数Tmk(iω)表示为

(1)

式中：ω为各阶频率的圆频率；φmr和φkr分别为第r阶振型中提取响应位置处(m点)和施加冲击荷载位置处(k点)的位移幅值；xm(iω)和fk(iω)分别为提取响应的Fourier变换和施加冲击荷载的Fourier变换；Hr(iω)为位移频响函数。

实际中，冲击荷载在一般桥墩结构的自振频率范围(<20 Hz)内满足白噪声条件，因此冲击荷载谱密度函数在频域内为定值C0，m点的响应可以表示为

(2)

从式(2)可以看出，当施加冲击荷载时，响应位置处的响应谱与其频响函数之间是倍数关系，两者具有相同的曲线形状，因此可以采用响应谱近似表示频响函数。

在采用速度响应谱的幅值和相位确定桥梁下部结构的自振特性时，在结构自振频率处，相位角为0°或180°[8]。

但冲击振动试验法并不能得到结构振型，而且冲击振动试验法只适用于桥墩各阶模态相间比较稀疏，相邻模态之间耦合性不强的情况，此时多自由度结构的频响函数可用一系列等于原结构各阶自振频率的单自由度结构的频响函数近似，如图1所示。当相邻模态之间耦合性较强，如果仍用单自由度频响函数近似表达多自由度频响函数，如图2所示，将很难准确识别下部结构的自振频率。然而高速铁路桥梁下部结构的频谱在低频段往往存在较密集模态，这为冲击振动试验法的应用造成了困扰。

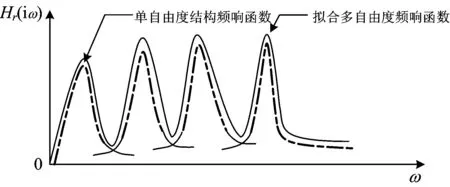
图1　模态相间稀疏时的单自由度和拟合多自由度频响函数

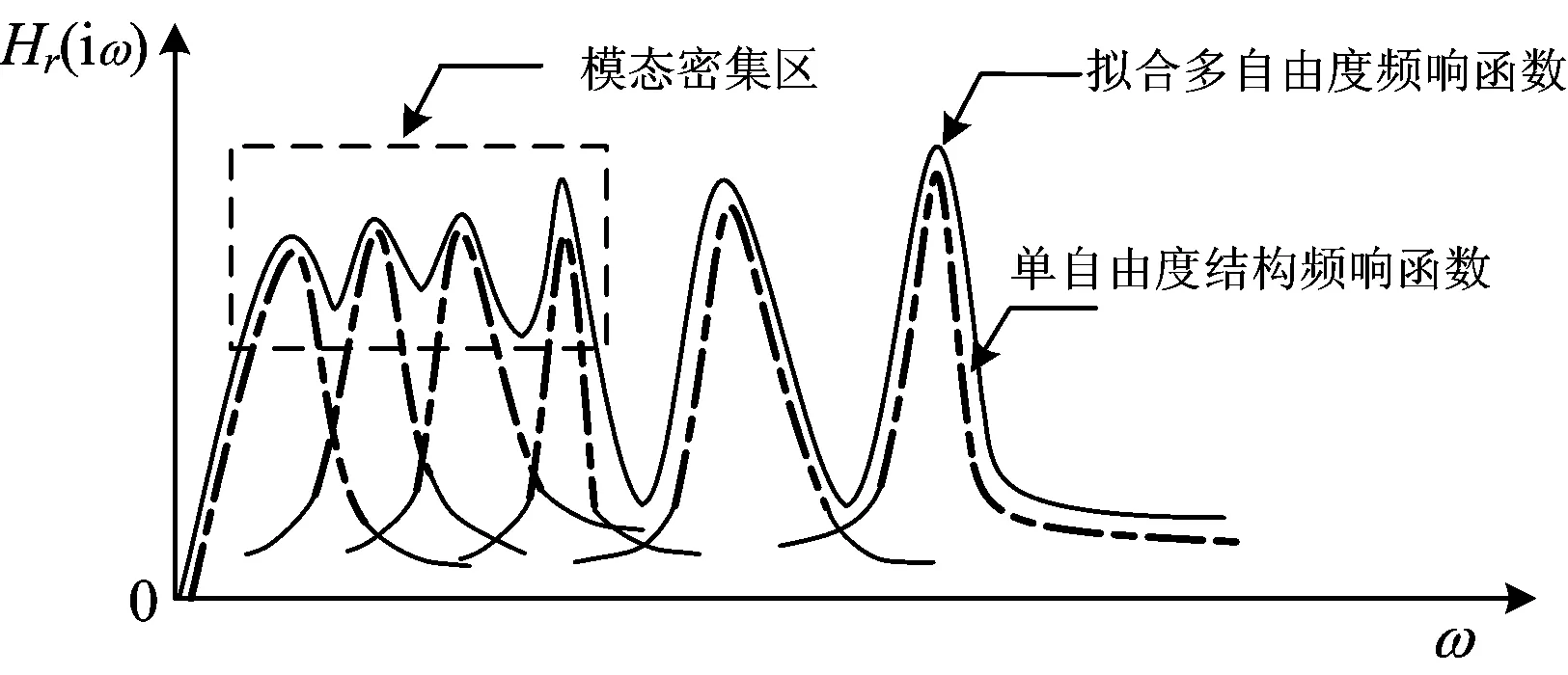
图2　模态相间密集时的单自由度和拟合多自由度频响函数

随机子空间法[9]是基于时域的模态分析方法，不依赖响应的频谱图。在求解过程中，引入卡尔曼滤波、奇异值分解(SVD分解)和正交三角分解(QR分解)等数学工具，得到系统矩阵，最终可直接确定结构的频率和振型。因此对于模态频率相间比较密集的情况，也能得到较好的结构频率和振型识别结果。

随机子空间法在实际工程应用中，由于受噪声等不确定因素的影响，系统矩阵模态阶次的获取较为困难。本文选取稳定图法[10]对系统阶次进行确定，具体方法如下。

(1)假定系统矩阵具有不同的阶次，得到多个不同阶次的状态空间模型。

(2)对每个状态空间模型进行模态参数识别，并将得到的所有模态参数绘制在稳定图中，以便确定正确的模态阶次和模态参数。

(3)将相邻2阶状态空间模型识别的模态参数进行对比，当模态频率、模态振型和阻尼比的差异小于预设值时，可将这个点作为稳定点，由稳定点组成的轴即为稳定轴，相应的模态即为结构的模态。

在绘制稳定图时，为了得到稳定的模态，需应用如下收敛准则：

(3)

其中，

式中：f，ξ和Φ分别为结构的频率、阻尼、振型；r为模态阶次；MAC为模态置信准则；εf，εξ和εΨ分别为频率容差、阻尼容差和振型容差。

频率容差、阻尼容差和振型容差的具体取值可根据实际工程情况和经验确定。当选取合理容差时，即可对各阶模态精确识别。

可见，随机子空间法较为繁琐，需要多个测点的响应信号，当对大量桥墩进行模态辨识时效率较低。

本文融合冲击振动试验法和随机子空间法的各自优势，采用多墩多测点(在相邻多个桥墩的墩顶、墩身、跨中、梁端等位置同时布置测点)和单墩单测点(在被测墩的墩顶布置测点)测试方案相结合，进行强耦合作用下高速铁路的多个桥梁下部结构的模态参数识别。

首先选择几组典型桥墩，采用图3所示流程对其振动模态进行精确识别，找到各阶频率和各阶振型的映射关系，进而得到典型桥墩各阶模态参数的数据样本。

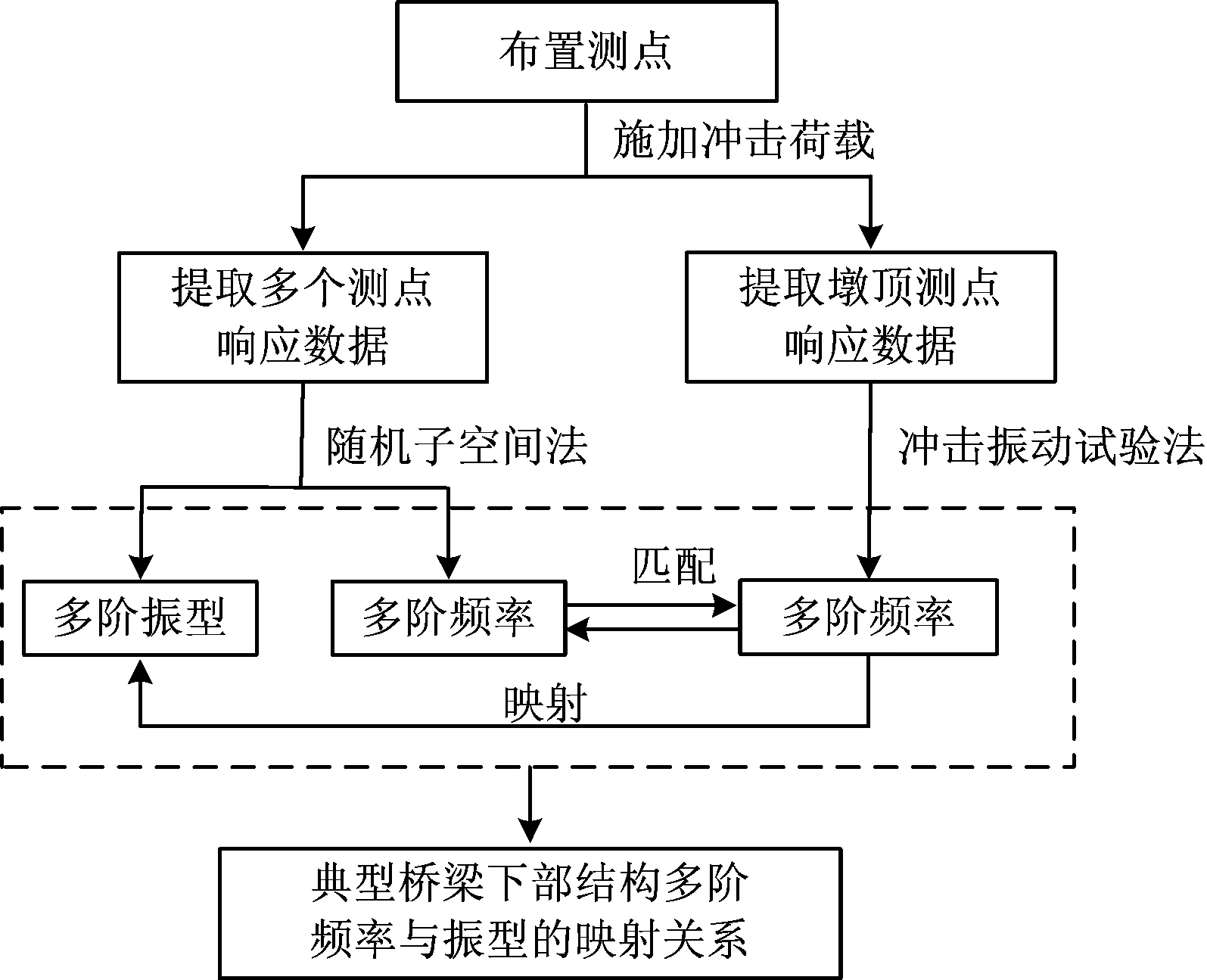
图3　桥梁下部结构模态识别流程图

然后通过冲击振动试验法得到其他桥墩各阶振动频率，再与数据样本对比，从而实现对其他桥墩模态的快速识别。

需要注意的是，本文方法主要适用于同结构体系多跨简支梁的多个桥梁下部结构的模态参数识别。

2　高寒地区高速铁路桥梁下部结构模态参数识别

选取高寒地区1座高速铁路多跨简支梁桥进行下部结构模态识别。测试区段内所选梁均为标准32 m简支箱梁，下部结构为圆端形桥墩，基础形式为桩基础，桩径均为1 m，桩长为32～44 m，桩的根数为8～10根。大部分桥墩所处地质条件均为黏质黄土或者砂土，仅有少量的桥墩基础布置在水中；试验所选桥墩的墩高为3～20.5 m。

该地区全年温度变化曲线如图4所示。依据图4可知该试验地区的冻土类型属于季节性冻土，且可将土体冻融过程分为4个阶段，具体见表1。

图4　2015—2016年测试区段月最高和最低温度曲线图

阶段土体状态时间1非冻土期 2015-05—2015-102冻胀快速发展期2015-11—2015-123冻胀稳定发展期2016-01—2016-024融化回落期 2016-03—2016-04

为了研究季节性冻土对桥梁下部结构模态参数的影响，对非冻土期(10月份，平均气温10 ℃)、冻胀稳定发展期(1月份，平均气温-20 ℃)、融化回落初期(3月份，平均气温0 ℃)和融化回落后期(4月份，平均气温10 ℃)的高铁桥梁进行现场测试。

经过多次实地考察，在充分考虑了墩身高度、桩长、桩的个数和地质条件等因素的基础上，除冻胀稳定发展期仅对其中一部分桥墩进行测试外，其他3次测试均选取相同的108个桥墩进行测试，其中对7组典型区段内的桥墩进行了多墩多测点测试，对73个非典型桥墩进行了单墩单测点测试，图5给出了453#—457#墩多点测试拾振器的布置情况。单墩单测点测试和多墩多测点测试分别采用INV3062T型24位4通道采集仪和INV3020型24位28通道采集仪进行数据采集。

试验中，以桥墩中间的上人梯为挂锤点，用外包硬质橡胶的重锤横向击打桥墩顶部，得到信噪比较高的冲击信号。

在455#墩的墩顶施加冲击荷载，并拾取该墩顶的横向速度响应，采用冲击振动试验法对其进行响应谱分析，结果如图6所示。由图6可见，该响应谱中存在多个峰值点且都满足相位角条件。

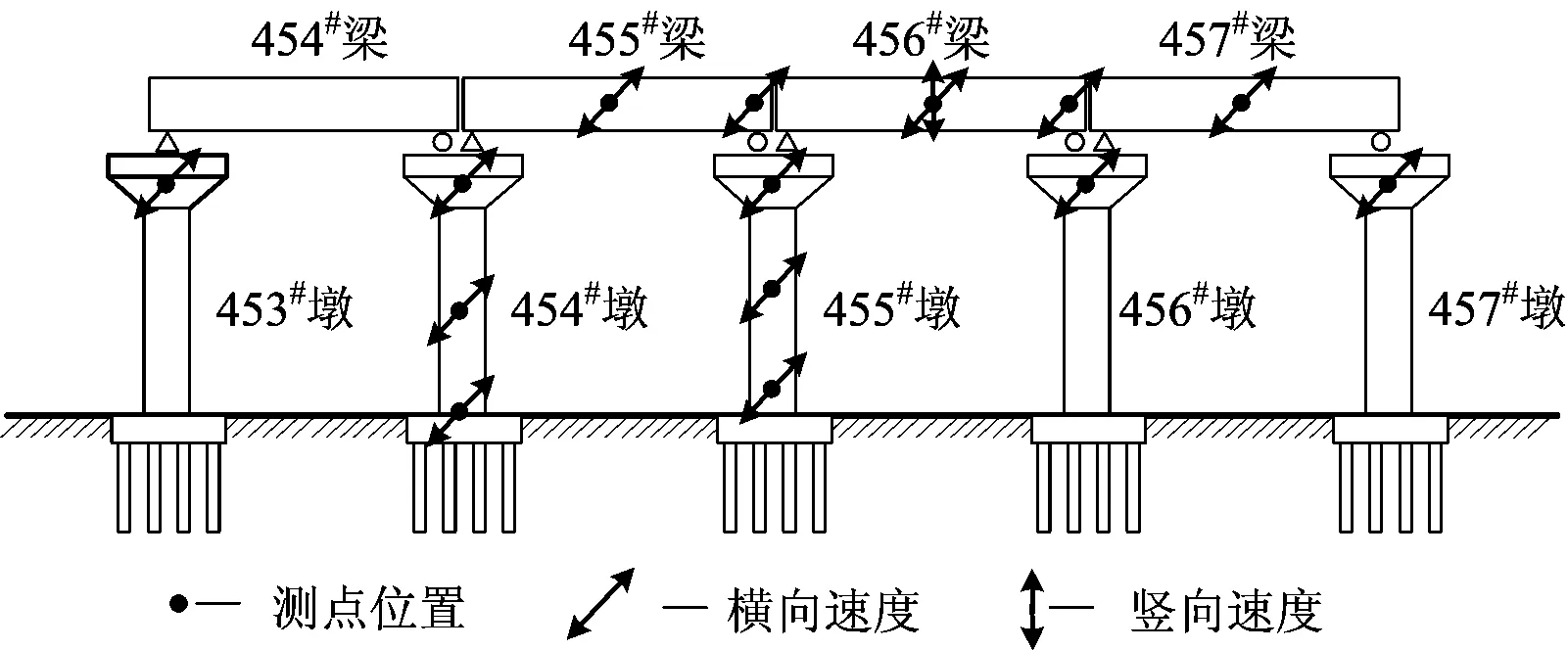
图5　多墩多测点测试拾振器布置图

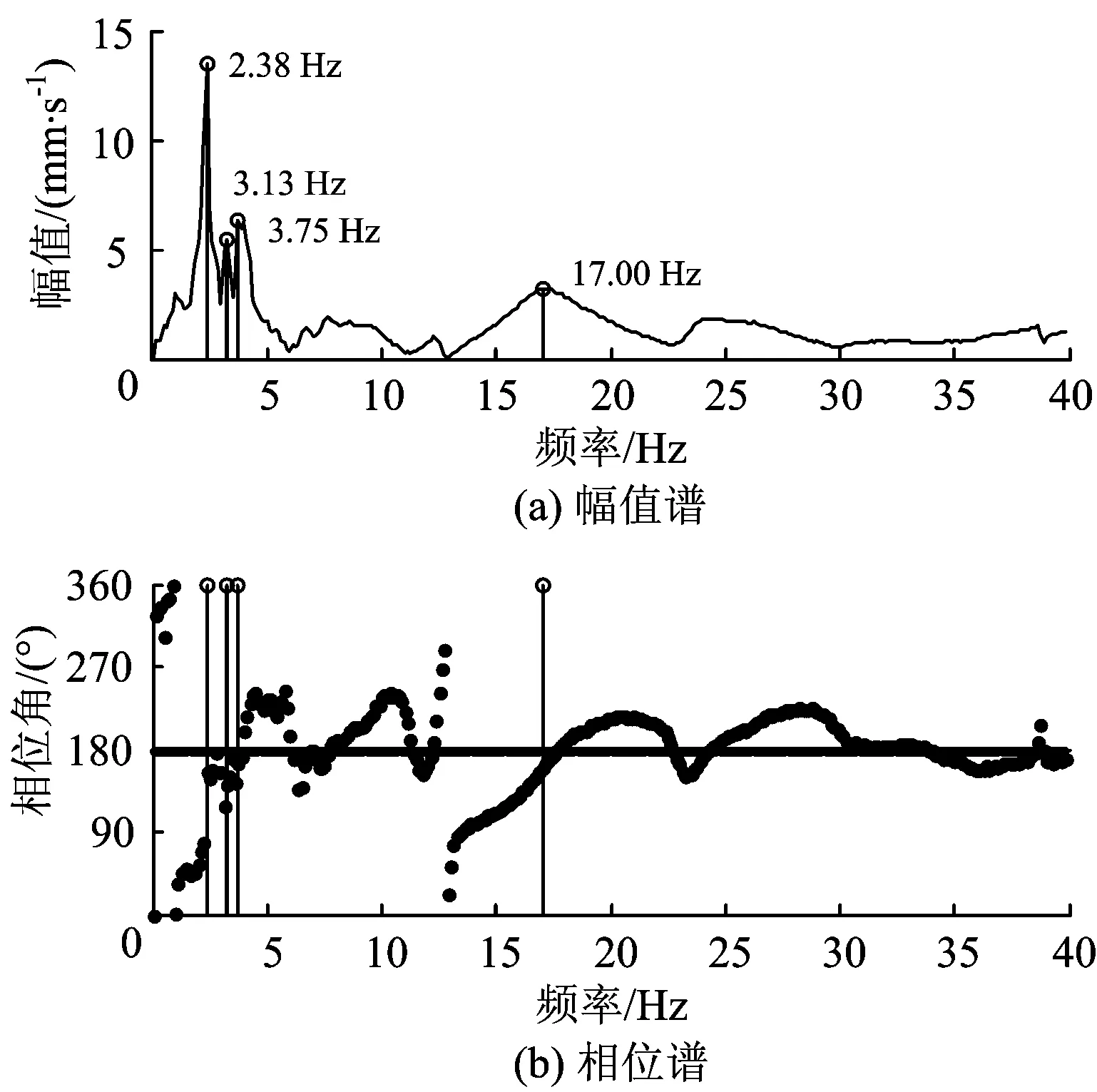
图6　455#墩的墩顶横向速度测点响应谱

根据非冻土期453#—457#桥墩多测点测试所得的桥梁速度响应，采用随机子空间法对桥梁下部结构进行模态参数识别，得到的稳定图如图7所示，其中频率、振型和阻尼比的容差分别取为1%，2%和5%，此时图中不同模态阶次的各稳定点组成的稳定轴即为桥梁各阶振动频率。综合各测点数据，即可得到各阶模态频率下的模态振型。

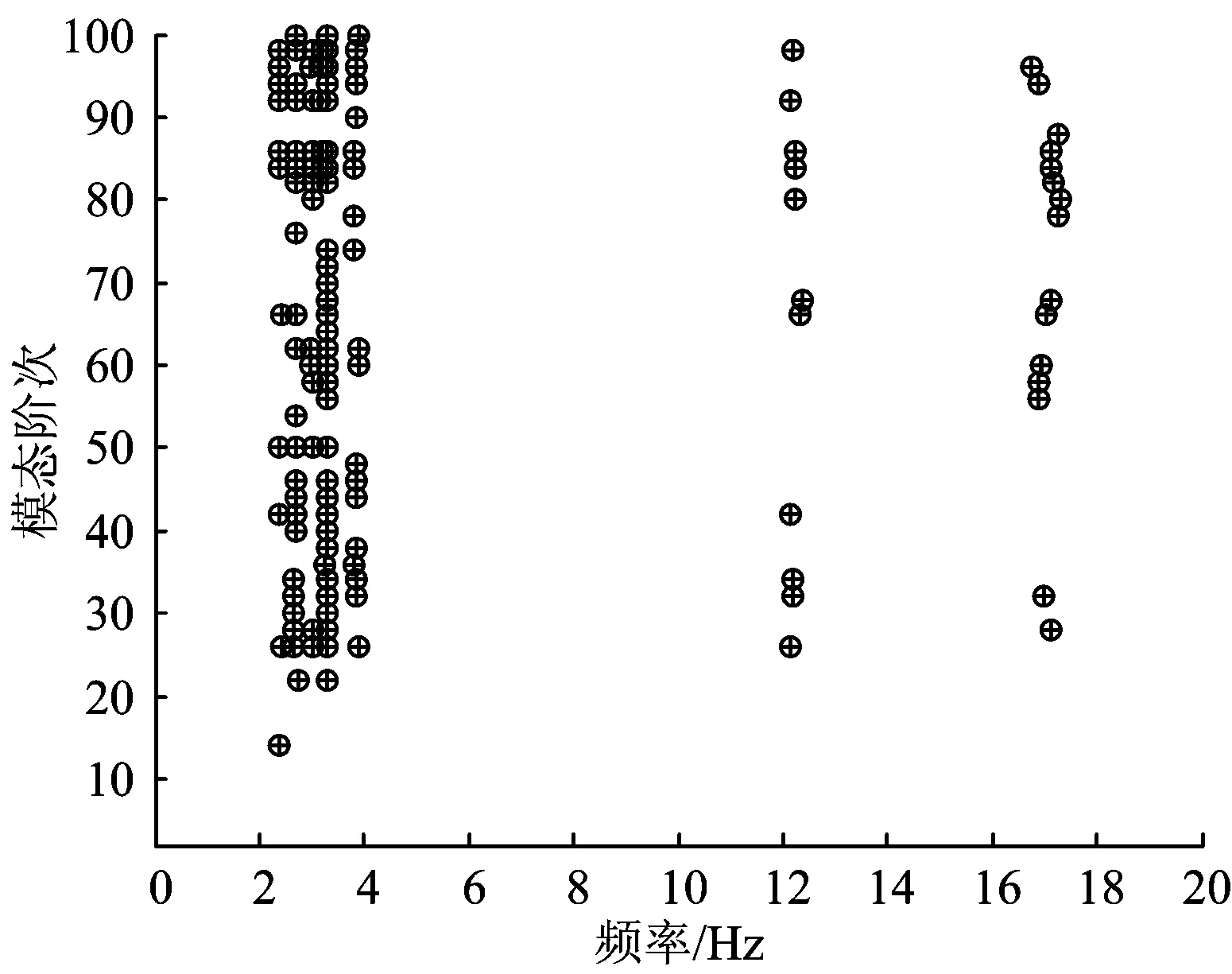
图7　稳定图

排除虚假模态的干扰(12 Hz左右为梁的扭转模态)，可得到以桥墩横向振动为主的4阶振动模态：全桥横向整体摆动模态、单墩横向整体振动模态(墩、梁同向)、全桥横向交错振动模态和单墩横向局部振动模态(墩、梁反向)。4种以桥墩为主的模态振动形式如图8所示。图8中数字代表横向速度测点编号：1～5号测点分别代表453#—457#墩顶测点；6号和7号测点分别为454#墩中和墩底测点；8号和9号测点分别为455#墩中和墩底测点；10号和11号测点分别为455#和456#梁跨中测点；12号测点为455#墩支座上方梁端测点。

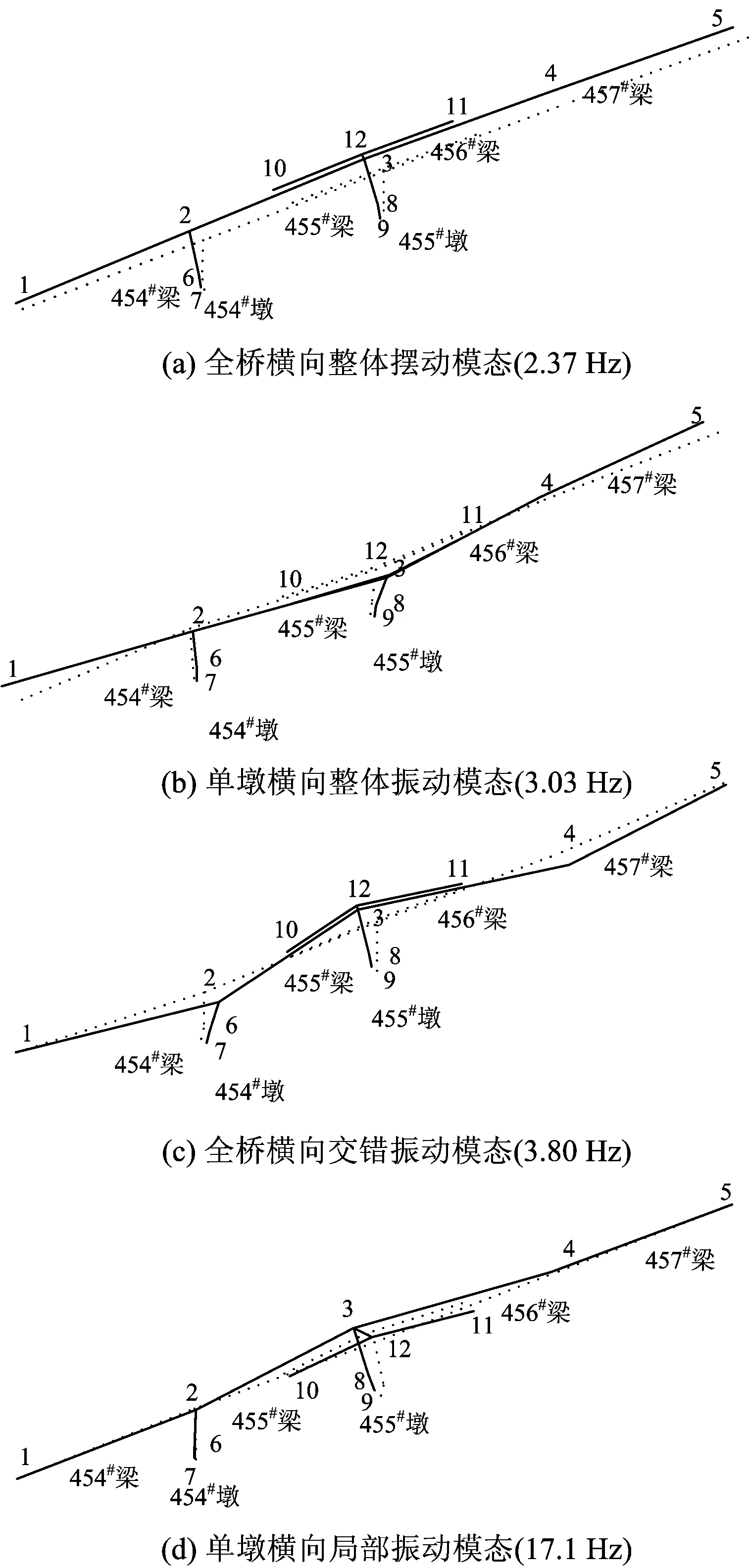
图8　桥墩实测振动模态

从图6和图8可知，模态分析得到的全桥横向整体摆动模态(2.37 Hz)、单墩横向整体振动模态(3.03 Hz)、全桥横向交错振动模态(3.80 Hz)和单墩横向局部振动模态(17.1 Hz)分别对应冲击振动试验法求得的响应谱中多个峰值中的4个峰值点2.38，3.13，3.75和17 Hz。

这2种方法的识别误差主要来自于以下几个方面：①采用冲击振动试验法对冲击响应信号进行分析时，频率分辨率的限制；②采用随机子空间法对信号进行处理时，矩阵运算的误差以及稳定图中稳定点的选取误差；③选取信号长度不同引起的误差。

根据455#墩响应谱峰值点的分布，可匹配得到其他桥墩的振动频率。456#墩墩顶横向速度响应谱如图9所示，其4阶横向振动频率分别为2.38，3.13，4.00和16.88 Hz。据此即可采用冲击振动试验法对单墩单测点测试方案下各桥墩的各阶模态进行快速、准确的识别。

图9　456#墩墩顶横向速度测点响应谱

3　冻融循环对下部结构模态参数的影响规律

3.1　基础冻结工况对桥墩模态参数的影响规律

高寒地区年温差较大，对于桥墩来说，模态参数的变化主要来源于基础冻结状况的变化，进而影响桥梁和列车的运营安全。

为了研究高寒地区基础冻结状况对高速铁路桥梁下部结构动力参数的影响规律，仍以455#墩为例，将未冻土期和冻胀稳定发展期的响应谱分析结果绘于图10。

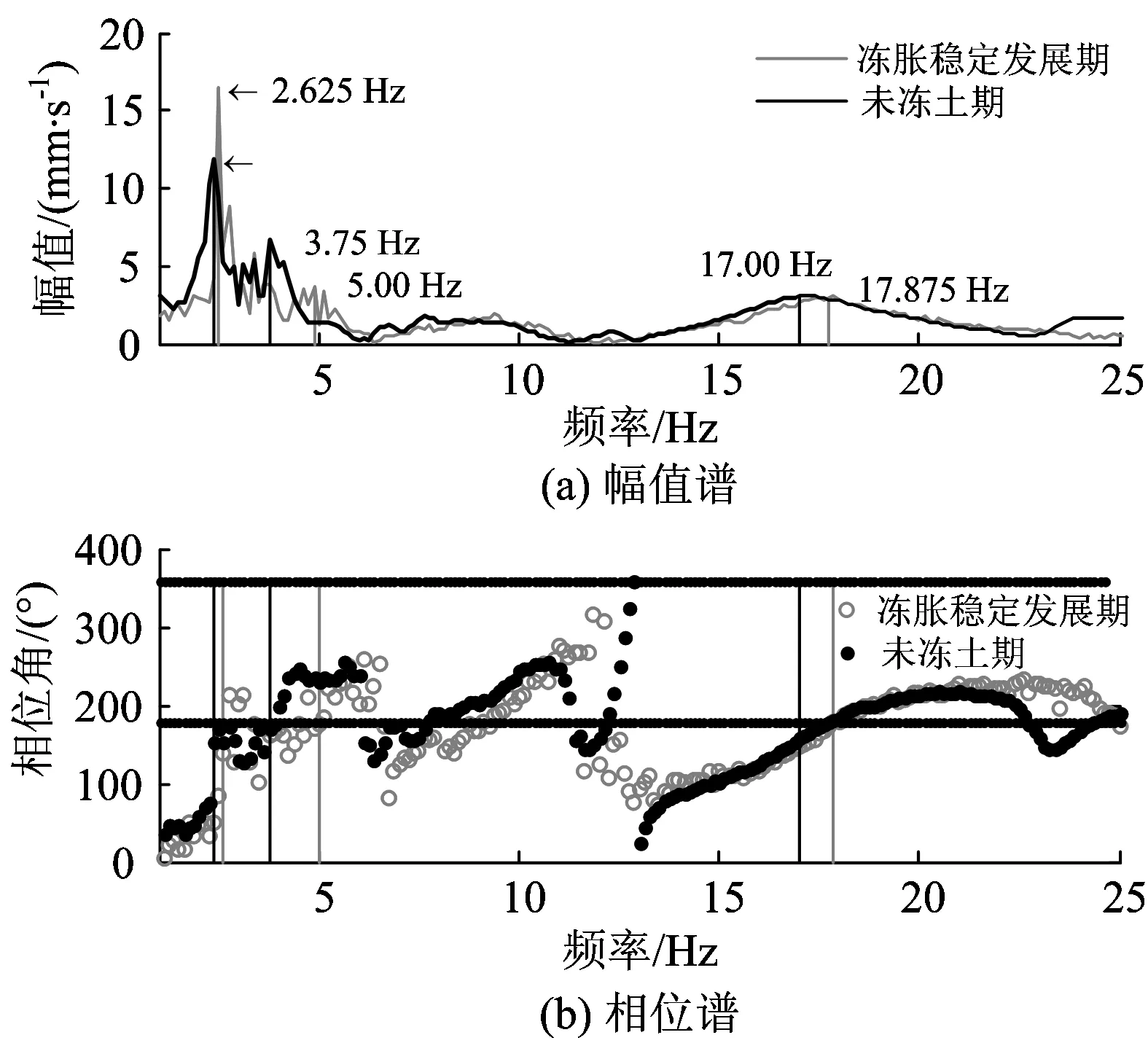
图10　不同时期455#墩响应谱

从图10可以看出，当土壤冻结时，桥梁下部结构的各阶频率均会发生较为明显的增大，且相位也会相应滞后。将455#墩不同时期的测试结果汇总于表2。根据前述频率和振型的映射关系，由测试模态分析结果得到了桥梁下部结构的4阶振动模态。其中1—4阶模态分别代表全桥整体摆动模态、单墩整体振动模态、全桥横向交错振动模态和单墩局部振动模态；频率增幅均以未冻结期的实测频率值为基准。

从表2可知，随着环境温度的变化，各阶模态均会发生周期性的变化。随着环境温度的降低，基础冻结深度不断增大，全桥横向交错振动模态的频率增大最为显著，冻结深度最大的1月份其频率增幅达到36.8%；其次是全桥整体摆动和单墩整体振动频率，增幅最小的是单墩局部振动频率，最大增幅仅有5%左右。

表2　455#墩不同时期模态识别结果

实际测试表明，单墩整体振动模态的信号幅值较小，在多数情况下较难测得。单墩横向局部振动模态指的是墩、梁发生相对振动时桥墩的振动模态，其频率与支座刚度有直接关系。当环境温度降低时，支座刚度和基础刚度均会增大，共同导致了该阶频率的增大。但是由于高铁桥梁支座刚度较大，获取该阶模态所需的能量也较大，一般也较难测得[11]。因此后文仅对全桥横向整体摆动模态和全桥横向交错振动模态进行讨论分析。

将68#墩、81#墩、186#墩和425#墩不同时期的模态识别结果绘于图11。从图11可以看出，随着基础冻结条件的改变，4个时期桥墩的全桥整体摆动模态和全桥横向交错振动模态均在发生变化，且冻胀稳定发展期频率最高，其次是融化回落初期、融化回落后期，频率最低的为未冻结期，其中，全桥整体摆动模态的变化范围在0.2～0.7 Hz，全桥交错振动模态的变化范围在0.8～2 Hz。

从组织学上看，8例显示黏膜病变，2例在HE染色下可见明显的伸入运动（图1A，B）现象，即组织细胞吞噬淋巴细胞、浆细胞或中性粒细胞的现象。高倍镜下可见，淡染区的组织细胞弥漫性增生，体积较大，胞浆丰富、淡染嗜酸性，其内可见淋巴细胞，浆细胞等（图1C）。低倍镜下，病变表现为明显的淡染区和深染区明暗交替相间（图1D），两种成分比例在不同病例上略有不同。

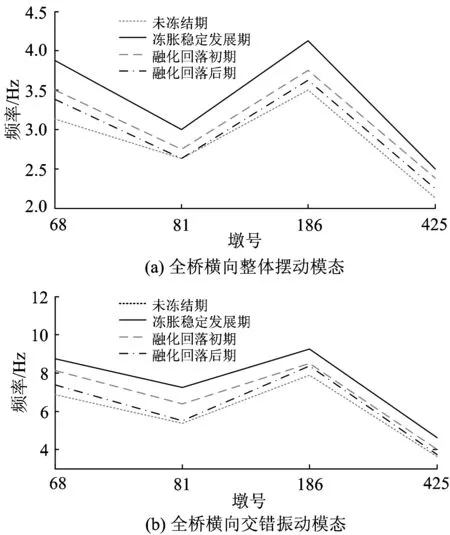
图11　桥墩4个时期的模态分析结果

3.2　桥墩设计参数对桥墩模态参数的影响规律

桥墩作为桥梁的重要组成部分，其各设计参数对冻融循环作用下桥梁下部结构模态参数变化规律有不同程度的影响。为了研究不同设计参数(墩高、桩长、桩的根数)对桥墩模态参数的影响程度，将测量得到的所有数据进行汇总，并采用数理统计中的R值检验法对设计参数与实测频率的相关程度进行分析，结果见表3。2个变量的相关系数由下式计算。

(4)

式中：cov(f1,f2)是变量f1和f2的协方差；D(f1)和D(f2)分别为变量f1和f2的标准差；f1和f2分别为桥梁下部结构各阶频率及其设计参数等变量。

从表3可以看出：①全桥整体摆动模态与全桥交错振动模态之间有很强的正相关性；②全桥整体摆动模态和全桥交错振动模态与墩身高度之间呈现明显的负相关关系，且其相关程度达到了80%以上；③全桥整体摆动模态和全桥交错振动模态与桩长、桩的个数之间的相关程度较低，基本维持在10%左右。

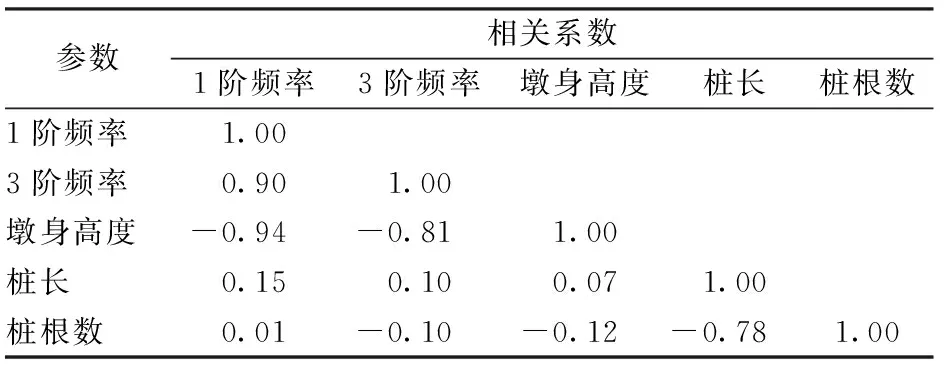
表3　相关系数汇总结果

当数据量大于62、置信度为95%时，相关系数临界值R0.95≤0.25，数据量越大相关系数的临界值越小。当计算所得的相关系数R>R0.95时，表明在置信度95%下具有显著相关性，且R值越接近1说明相关性越好[12]。本次测试的各组数据量都在100个左右，根据表3分析结果，说明墩高对高速铁路桥梁下部结构频率的影响十分显著，其他桥墩设计参数对其影响可忽略不计。为此，仅就墩高对桥墩模态参数的影响规律进行分析研究。

为了研究墩高在冻融循环作用下对桥梁下部结构模态参数的影响规律，将不同时期典型桥墩的全桥横向整体摆动模态和全桥横向交错振动模态的分析结果进行汇总。由于在冻胀稳定发展期只对少量桥墩做了现场测试，数据量较少，在这里不作统计。

为了更加直观地显示各阶模态频率与墩高之间的统计关系，对各组数据进行回归分析，回归方程为

fy=β1-β2lnh

(5)

式中：β1和β2分别为回归系数；h为各桥墩墩高；fy为线性回归后各墩高下各阶频率的预测值。

通过以上回归，可得到各阶频率的回归表达式，实测频率值和频率回归曲线如图12所示。对各墩高下的拟合频率值与实测频率值进行相关系数分析，可得其相关程度均在85%以上，说明该回归结果能够较好地反映实测频率随墩高的发展趋势。

从图12中可以看出：

(1) 无论是全桥横向整体摆动频率还是全桥横向交错振动频率，同一时期随着墩身高度的增加，桥梁下部结构的各阶频率都有逐渐减小的趋势。再次验证了墩高对桥梁下部结构模态参数有较大影响。

(2) 不同墩高的全桥横向整体摆动频率均处于2～4 Hz之间，全桥横向交错振动频率处于3～9 Hz之间，说明墩高对全桥横向交错振动模态的影响大于全桥横向整体摆动模态。

(3) 对比3个时期模态分析结果，融化回落初期的频率最高，其次是融化回落后期，未冻结期的频率最低。说明当环境温度降低时，桥梁下部结构的频率会有显著增大的趋势，这是由于冻土对桥墩基础约束增强导致的。

(4) 随着墩高的增加，冻融循环对全桥横向整体摆动模态的影响逐渐降低。这是因为当墩高较高时，墩身刚度较小，该阶模态主要受到墩身刚度的制约，对冻结深度并不敏感；对于全桥横向交错振动模态来说，冻融循环对不同墩高的桥墩均有较为明显的影响。

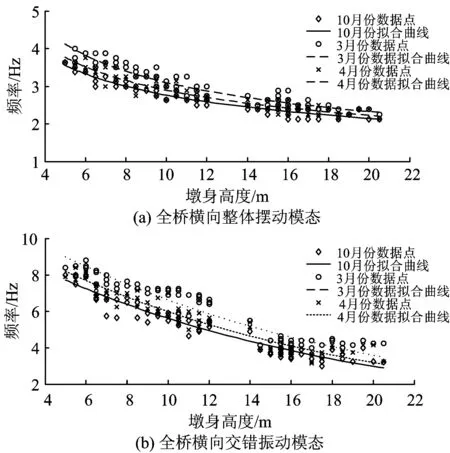
图12　不同时期模态分析结果汇总

3.3　桥墩基础环境对桥墩模态参数的影响规律

冻融循环作为一种温度变化的具体形式，可以被理解为是一种特殊的强风化作用形式，对土体的物理力学性质有着强烈的影响。地质条件不同，冻融循环对其作用的机理也不尽相同。

本次试验所选区段内大部分桥墩所处的地质条件均为黏质黄土或者砂土，仅有少量的桥墩基础布置在水中。高寒地区高速铁路在设计修建过程中，为避免基础承受冻胀力的破坏作用，要求基础底面埋深在土壤最大冻结深度(205 cm)以下。图13为现场某水中桥墩。为了提高水中桥墩混凝土抗冻等级，在其底部安装了耐候钢板，但该桥墩的承台裸露在外，不满足抵抗冻胀力的要求。

图13　水中墩现场照片

为了研究不同地质条件对桥梁下部结构模态参数的影响规律，对其他条件相同的水中墩和非水中墩(墩高均为20 m)进行分析，分析结果如图14所示。

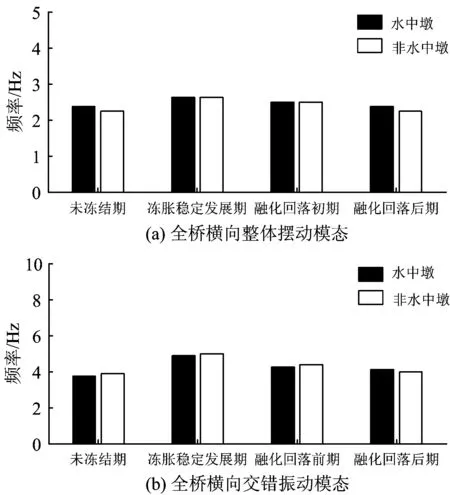
图14　水中墩与非水中墩各时期的频率对比图

从图14可以看出：

(1) 当基础冻结条件发生改变时，水中墩和非水中墩的各阶频率变化差异不大，说明冻融循环作用下地质条件对桥墩的频率几乎没有影响。

(2) 相同时期水中墩的各阶频率均与非水中墩的测试结果较为一致。说明目前来看，该水中墩并未发现较为严重的病害。这是因为高速铁路在我国运营时间较短，桥梁结构出现的问题还不是特别突出，但随着运营时间加长、桥梁服役年限增加以及自然条件和各种因素的影响，尤其对于水中桥墩，高速铁路桥梁很容易出现状态退化的现象，从而影响桥梁的整体服役性能。因此需要对水中墩进行长期密切监测。

4　结　论

(1) 随着冻结深度的增加，桥墩各阶横向振动频率均会增大，且全桥横向交错振动频率的增大趋势最为显著，最大增幅达到36.8%。

(2) 随着基础冻结条件的改变，4个时期桥墩的全桥整体摆动模态和全桥横向交错振动模态均在发生变化，其中全桥整体摆动频率的变化范围为0.2～0.7 Hz，全桥横向交错振动频率的变化范围为0.8～2.0 Hz；4个时期中，冻胀稳定发展期的频率最高，其次是融化回落初期、融化回落后期，频率最低的为未冻结期。

(3) 墩身高度是影响高铁桥梁下部结构模态频率的主要设计参数，其相关系数达到了80%以上，随着墩身高度的增加，桥梁下部结构的各阶频率逐渐减小，且冻融循环对全桥横向交错振动模态的影响大于全桥横向整体振动模态，其中全桥横向交错振动频率的范围为3～9 Hz，全桥横向整体振动频率的范围为2～4 Hz。

(4) 地质条件对桥墩模态参数的影响并不明显，但在后续的桥梁运营维护中，需对冻融循环作用下的水中墩进行长期密切的监测。

[1]魏召兰. 高速铁路大型桥梁结构健康监测与状态评估研究[D].成都：西南交通大学,2012.

(WEI Zhaolan. Research on Health Monitoring System and Condition Assessment of Large-Scale High-Speed Railway Bridge Structure [D]. Chengdu：Southwest Jiaotong University, 2012. in Chinese)

[2]RICARDO Perera, ANTONIO Ruiz. A Multistage FE Updating Procedure for Damage Identification in Large-Scale Structures Based on Multi Objective Evolutionary Optimization[J]. Mechanical Systems and Signal Processing,2008,22:970-991.

[3]中华人民共和国铁道部.铁运函[2004]120号 铁路桥梁检定规范[S].北京：中国铁道出版社,2004.

[4]辛峻峰，盛进路，张永波. 数据驱动随机子空间法矩阵维度选择与噪声问题研究[J]. 振动与冲击,2013,32(16),152-157.

(XIN Junfeng, SHENG Jinlu, ZHANG Yongbo. Relation between Noise and Matrix Dimension of Data-Driven Stochastic Subspace Identification Method[J]. Journal of Vibration and Shock, 2013,32(16),152-157. in Chinese)

[5]李中付，宋汉文，华宏星，等. 一种白噪声环境激励下模态参数辨识方法[J]. 振动工程学报,2002,15(1)：52-56.

(LI Zhongfu, SONG Hanwen, HUA Hongxing,et al. A Method of Modal Parameter Identification under White Noise Excitation [J]. Journal of Vibration Engineering, 2002,15(1)：52-56. in Chinese)

[6]战家旺. 既有铁路桥墩健全度评估和试验方法研究[D]. 北京：北京交通大学, 2006.

(ZHAN Jiawang. Soundness Evaluation and Experiment Method Studies on Existing Railway Piers [D].Beijing：Beijing Jiaotong University, 2006. in Chinese)

[7]闫宏业，蔡德钩，杨国涛，等. 高寒地区高速铁路路基冻深试验研究[J]. 中国铁道科学,2015,36(3)：1-6.

(YAN Hongye, CAI Degou, YANG Guotao, et al. Experimental Study on Frost Depth of High Speed Railway Subgrade in Cold Region [J]. China Railway Science, 2015,36(3)：1-6. in Chinese)

[8]战家旺，夏禾，姚锦宝. 既有桥梁墩台自振频率测试的冲击振动试验法[J]. 北京交通大学学报,2005,29(1)：14-17.

(ZHAN Jiawang, XIA He, YAO Jinbao. An Impact Vibration Test Method for Measuring Natural Frequencies of Existing Piers[J]. Journal of Beijing Jiaotong University, 2005,29(1)：14-17. in Chinese)

[9]秦世强. 桥梁健康监测与工作模态分析的理论和应用及系统实现[D]. 成都：西南交通大学,2013.

(QIN Shiqiang. Bridge Health Monitoring and Operational Modal Analysis: Theory, Application and Implementation [D]. Chengdu:Southwest Jiaotong University, 2013. in Chinese)

[10]刘东霞. 基于随机子空间法的梁桥模态识别[D]. 成都： 西南交通大学,2005.

(LIU Dongxia. Modal Parameter Identification of Girder Bridge Based on Stochastic Subspace Algorithm[D]. Chengdu:Southwest Jiaotong University,2005.in Chinese)

[11]战家旺，王伟，张楠，等. 基于模型修正理论的铁路桥墩损伤定量评估方法[J]. 中国铁道科学,2015,36(5)：28-35.

(ZHAN Jiawang, WANG Wei, ZHANG Nan, et al. Quantitative Damage Evaluation Method for Railway Piers Based on Model Updating Theory [J]. China Railway Science, 2015,36(5)：28-35. in Chinese)

[12]焦志钦，胡利平，韩大建. 温度对桥梁动力特性的影响研究[J]. 科学技术与工程,2010,10(31)：7685-7689.

(JIAO Zhiqin, HU Liping, HAN Dajian. Research on the Influence of Temperature Effects on Bridge Modal Properties[J]. Science Technology and Engineering, 2010,10(31)：7685-7689. in Chinese)