低体积含量的钢纤维混凝土三折线拉应变软化曲线的确定

安蕊梅， 段树金

(石家庄铁道大学 土木工程学院，河北 石家庄 050043)

低体积含量的钢纤维混凝土三折线拉应变软化曲线的确定

安蕊梅， 段树金

(石家庄铁道大学 土木工程学院，河北 石家庄 050043)

以带切口的钢纤维混凝土三点弯曲梁为研究对象，假定钢纤维混凝土的拉应变软化曲线为三折线形式，根据材料基本力学性能指标和初始裂纹失稳时实测的应变分布，建立韧带所在截面的力平衡方程，通过联立方程求解，得到钢纤维混凝土的拉应变软化曲线系数，并可以直接通过韧带上距裂尖第二道应变片拉断时的应变分布和对应荷载，利用弯矩平衡方程验证计算系数的正确性；最后以一低体积含量的钢纤维混凝土试验梁为计算实例，验证了这种方法的可行性。

钢纤维混凝土；拉应变软化曲线；三折线模型；力平衡方程

0 引言

钢纤维混凝土做为一种新型的混凝土材料，在桥梁、隧道、路面工程中应用越来越广泛。由于钢纤维对混凝土基体的阻裂、增韧效果，材料的拉压性能与普通混凝土有所不同，抗拉强度和极限拉应变都有明显提高[1-2]，拉压强度比比普通混凝土要小，而且材料性能与钢纤维体积含量、钢纤维的种类以及直径的影响非常明显。钢纤维混凝土的拉伸软化曲线，作为材料的一项基本性能，能直观反映材料对裂缝的抵抗能力和受拉破坏的延性，软化曲线的形状和规律成为当前对钢纤维混凝土研究的一个焦点内容。研究方法与普通混凝土的研究方法类似。混凝土拉伸软化曲线确定的方法，目前常见的有根据荷载-裂纹嘴张开位移的逆推法、直接拉伸法和基于实测COD和加权积分法的半解析法[3]。文献[3-4]通过试验研究了钢纤维混凝土的材料性能和断裂性能基本特点；文献[5]利用反分析法(逆推法)，根据试验的荷载位移曲线，对钢纤维混凝土的拉伸软化曲线进行了研究，并将软化曲线近似为三折线，认为计算结果比较吻合，但没有软化曲线的表达式，关键控制点没有给出；文献[6]对钢纤维混凝土构件破坏过程进行了观测，得到了应力和裂纹尖端张开位移的一些有用的结论，但依然没有表达式；文献[7]通过试验和数值模拟，分析了钢纤维的布置方式和长度对拉伸软化曲线的影响。可以看出，因为钢纤维混凝土拉伸软化曲线的影响因素很多，很难给出一个合理的表达式，要获得钢纤维混凝土的拉应变软化曲线的表达式，需要进行针对不同参数的大量试验。

本文力求寻找一个比较简便、合理的方法，得到钢纤维混凝土软化曲线的表达式，然后通过将来大量的试验验证和数值分析，力求能得到一个适用于任一钢纤维体积含量对应的软化曲线表达式。通过对一片低体积含量的钢纤维混凝土三点弯曲梁在裂纹失稳时的实测数据，以力平衡条件为基础，提出一种新的获得拉应变软化曲线的方法，同时实测数据能直接验证拉应变软化曲线的正确性。

1 钢纤维混凝土带切口三点弯曲梁的受力过程和裂纹失稳特点

试验证明[8-11]，混凝土类材料的梁，受拉边缘达到抗拉强度后，不会马上开裂，而是在最大拉应力附近区域发生拉应变软化，出现裂纹的亚临界扩展，形成了断裂过程区；随着拉应变的不断增加，断裂过程区基体混凝土之间的粘结应力不断减小直至零，真实裂纹出现或失稳。断裂过程区中混凝土之间的粘结应力与拉应变之间的关系曲线称为拉应变软化关系曲线。拉应变软化曲线是材料的基本力学性能，它体现在结构的任何受力情况下。

当梁的缝高比较小且梁高达到一定值时，三点弯曲梁的断裂试验数据稳定，塑性区可以被弹性区完全包围[1]，得到的试验现象和结果能比较好地反映材料的断裂性能。

根据钢纤维混凝土梁的试验[2-5]和虚拟裂纹理论，在较小的竖向荷载作用下，裂纹所在截面处于弹性阶段，裂尖的拉应力和拉应变均大于名义值，即有很大的应力和应变集中，且两种集中系数相同。随着荷载的加大，裂尖的应力超过了钢纤维混凝土抗拉强度，拉应变达到了峰值拉应变，此时钢纤维的阻裂作用开始体现，同时裂尖混凝土进入塑性工作阶段，拉应力不断减小，拉应变增加加快，中性轴不断向受压边移动，整个裂纹所在截面发生了应力重分布。荷载继续加大，裂纹尖端拉应力减小至零，此时钢纤维混凝土达到了极限拉应变，应变片拉断，同时钢纤维与基体混凝土的粘结发生破坏，裂纹尖端张开位移(COD)达到临界值，三点弯曲梁的断裂过程区长度发展到最大，此时的荷载为开裂荷载，裂纹失稳并延伸。

图1 三点弯曲梁

当裂纹尖端出现塑性时，韧带截面上裂尖附近的拉应变明显加大同时韧带以外正截面的拉应变明显由于弹性回缩而减小，这也是判断裂尖出现塑性的一个标志。

改变初始裂纹长度、钢纤维体积含量，断裂性能会有所改变，但规律基本一致。

在韧带截面垂直于韧带粘贴合适标距的应变片同时，在距离韧带较近的另一个正截面也粘贴足量的应变片，可以获得荷载不断加大时韧带截面和旁边截面的应变分布规律，获得韧带截面中性轴位置和裂纹失稳时的平均极限拉应变，也可以获得构件断裂的裂纹临界长度和破坏时的受拉、受压区长度。

2 由裂纹失稳时的实测数据确定三折线拉应变软化曲线

对于带切口的钢纤维混凝土三点弯曲梁，当裂纹初始长度和钢纤维特征参数均一定时，拉应变软化曲线和开裂荷载存在对应关系。

如果梁的缝高比较小，裂纹开始扩展至失稳，裂纹尖端的塑性区都被弹性区完全包围，则荷载作用下裂纹尖端的塑性区、断裂过程区发展均比较完整，裂纹失稳时裂尖拉应变即为材料的极限拉应变εtu0，裂纹失稳时的荷载为开裂荷载，对应的弯矩为开裂弯矩Mcr。

设混凝土拉应变软化曲线为三折线。根据试验梁的应变和荷载测试结果，结合虚拟裂纹模型的观点，可以得到开裂弯矩的计算图式，见图2。

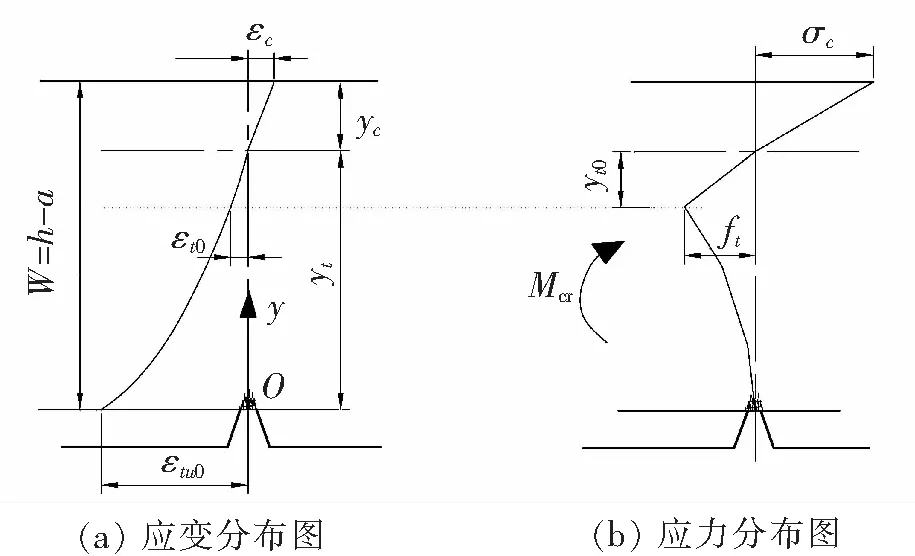
图2 开裂弯矩计算图式

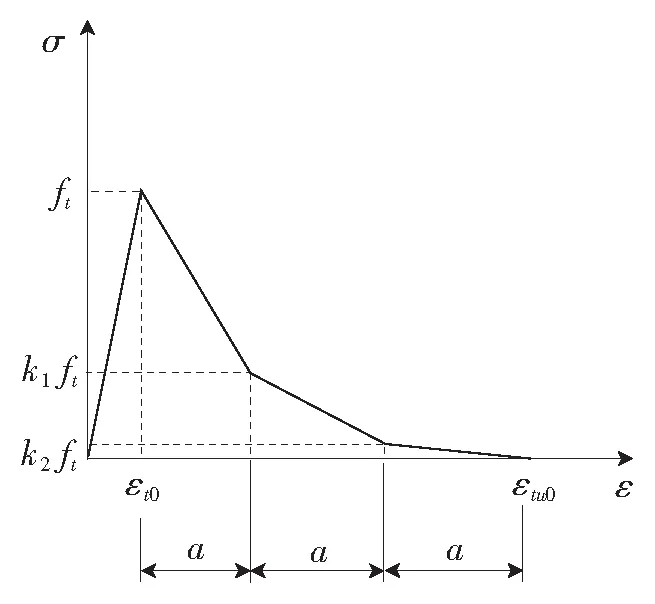
图3 混凝土应力应变关系曲线

计算假定：

(1)裂纹失稳时受压混凝土应力呈线性分布[6]，受压边缘δc=εcEc；

(2)混凝土拉应力-应变关系曲线如图3所示，表达式为

(1)

式中，系数k1、k2待定；εt0为峰值拉应变，由实测的ft和混凝土弹模算得；εtu0为实测极限拉应变。

(3)根据测试结果，得到混凝土拉应变沿梁高分布规律ε=ε(y)。

由力平衡条件计算，有

(2)

对中性轴求力矩，有

(3)

各参数yt、yc、εc、εtu0由裂纹失稳时应变分布得到，yt0由实测的ft、Ec和应变分布规律求得。由式(1)、式(2)、式(3)联立可得到系数k1、k2。

初始裂纹失稳后，裂纹继续扩展延伸至断裂。记录任一时刻韧带上应变片的应变分布和对应的荷载，将计算得到的软化曲线表达式代入式(3)，可以直接验证软化曲线的正确性。

改变梁的尺寸参数，如初始裂纹长度、宽度、高度，改变材料参数，如强度、钢纤维体积含量、钢纤维直径等，结合试验结果，会得到不同尺寸和材料参数下的拉伸软化曲线的特点和规律。

3 计算实例

为了保证数据的稳定性，保证塑性区能完全被弹性区包围，梁的宽度b和韧带长度W应该足够大[1]。为此，设计试验梁尺寸为b×h=150 mm×200 mm，计算跨度为620 mm，在跨中截面埋设薄钢片预制正裂纹，裂纹长度a0=50 mm，缝高比a0/h=0.2。

梁的钢纤维体积掺量为0.5%，乱向分布，钢纤维长度为3 cm，直径为1 mm，钢纤维的特征参数V/d=0.5。

制作了立方体和棱柱体试块，测得的钢纤维混凝土的材料性能参数为:fcu=51.5 MPa，fc=41.07 MPa，弹性模量Ec=2.65×104MPa。

在梁两侧面粘贴应变片11个，其中裂纹尖端近距离布置两个应变片以准确测定裂纹尖端应变发展特点，应变片标距应该大于裂纹尖端塑性区尺寸，本试验取5 cm，数据分析时取两面对应应变片测试值的均值；梁底安装数字位移计测试位移随荷载变化规律。

梁尺寸及应变片的布置如图4所示，B截面为预制裂纹所在截面，应变由1～7应变片测得；A截面应变由8～11应变片测得。

为了捕捉裂纹发展过程中裂纹尖端塑性区，荷载采用逐级缓慢加载的方式施加，用压力传感器记录施加的荷载大小。测得的应变分布发展情况如图5所示。图5(a)中的每一条曲线代表对应荷载下韧带截面的正应变分布，正值在水平轴上方，表示拉应变，负值表示压应变；曲线越靠近水平轴，对应的荷载越小，随着荷载的加大，曲线越来越远离水平轴，表明正应变越来越大；荷载增加到一定程度，拉应变片断裂，表明裂纹发展到了应变片位置处。图5(b)中的曲线为韧带以外A截面的正应变分布图，从图中可以看出，裂纹尖端出现塑性区之前，荷载增加，应变也增加；出现塑性区以后，荷载加大，A截面的正应变减小，黑色粗虚线表示荷载增加到裂纹失稳时的应变，应变值非常小。

图4 三点弯曲梁及应变片布置图(单位：mm)

图5 两个截面的不同荷载下的应变分布

试验中初始裂纹失稳时，7号应变片拉断，由韧带上实测应变分布拟合的应变分布曲线为：

ε=-0.001 1y3+0.489 4y2-83.726y+4 689(y为距离裂尖的高度，单位取mm)；εc=0.000 418，εtu0=0.004 598，yt=106.17mm，yc=43.83mm，ft=5.6MPa，Ec=2.65×104MPa，由测试的应变规律得到εt0=0.000 214，开裂荷载为16.16kN，开裂Mcr=2.52kN·m。

由式(1)、式(2)、式(3)联立求得： k1=0.252,k2=0.118。

下面是对计算结果的验证。距离裂纹尖端19mm的6号应变片拉断时的应变分布规律为：

ε=-0.002y3+0.790 9y2-117.47x+616 0.3(145mm>y>19mm)，yt=119.7mm，yc=30.3mm，εc=0.000 453，εt0=0.000 214，yt0=13.8mm。此时实测的弯矩为2.14kN·m。将计算的软化曲线表达式代入式(3)，计算得到的开裂弯矩Mcr=1.93kNm，与实测的弯矩比较，相对误差小于10%。

分析计算结果有误差的原因，主要有以下几点：

(1) 应变片的标距长度和应变片的间距决定应变分布规律。垂直于韧带的应变片长度范围内，拉应变变化剧烈，尤其在裂纹尖端附近，裂纹尖端拉应变最大，离裂纹尖端越远，拉应变迅速减小。在保证应变片能跨越裂纹的条件下，应变片长度越短，越能反映韧带截面的真实拉应变。应变片间距越小，测试的应变分布越准确。这项误差是主要原因。

(2)试验梁的各项尺寸误差。初始裂纹实际长度与设计时的误差、梁的实际跨度和计算跨度的误差都会影响计算结果。试验梁制作时应保证制作质量和精度。

(3) 材料性能测试误差。试块测试的材料性能和试验梁的材料性能的差异对计算结果有一定影响。

(4)基本假定带来的误差。将受压区和受拉区断裂过程区以外区域简化为弹性工作会带来一定误差。

4 结论

根据裂纹失稳时的荷载和应变分布确定拉应变软化曲线的方法适用于所有准脆性材料。对于不同尺寸、不同缝高比、不同钢纤维体积含量情况下的拉应变软化曲线，还需要更多的试验研究。

使用这种方法确定拉应变软化曲线，有几点需要注意：

(1) 要比较准确测试韧带和韧带附近正截面的应变分布及对应的荷载大小。应变片标距长度宜大于粗骨料直径且小于裂纹尖端塑性区宽度， 应变片布置间距要尽量小。

(2) 试验梁的初始裂纹的缝高比要比较小，保证裂纹尖端的塑性区能被弹性区完全包围而充分发展。

(3) 试验梁制作要保证尺寸精度。

(4) 测试材料性能的试块要严格保证和试验梁在制作、养护、加载方面条件相同。

[1]易成，谢和平，孙华飞. 钢纤维混凝土疲劳断裂性能与工程应用[M]. 北京：科学出版社，2003：21-31.

[2]刘永胜,王肖钧,金挺，等.钢纤维混凝土力学性能和本构关系研究[J].中国科学技术大学学报，2007，37(4)：717-722.

[3]朱海堂,高丹盈,谢丽,等. 钢纤维高强混凝土弯曲韧性的研究[J].硅酸盐学报，2004，32(5)：657-660.

[4]Ruimei An, Shujin Duan, Quanming Guo. New method to determine tensile strain softening curve of quasi-brittle materials[C]//ASEA-SEC-2, Sustainable Solutions in Structural Engineering and Construction.[S.l.]:[s.n.],2014:897-903.

[5]Ali Nour, Bruno Massicotte, Renaud de Montaignac, Jean-Philippe Charron. Development of an inverse analysis procedure for the characterisation of softening diagrams for FRC beams and panels[J]. Construction and Building Materials,2015,94(9):35-44.

[6]Ng T S, Htut t N S, Foster S J. Mode I and II fracture behaviors of steel fiber reinforced high strength geopolymer concrete: an experimental investigation [C]//Preceeding of Fracture Mechanics of Concrete and Concrete Structures. Korea:[s.n.],2010:1504-1511.

[7]Doo-Yeol Yoo, Su-Tea Kang, Young-Soo Yoon. Effect of fiber length and placement method on flexural behavior, tension-softening curve, and fiber distribution characteristics of UHPFRC[J].Construction and Building Materials, 2014,64(8):67-81.

[8]赵志方,王刚,周厚贵，等.混凝土拉伸软化曲线确定方法的对比研究[J]. 浙江工业大学学报，2015，43(4)：455-459.

[9]李夕兵,罗章,赵伏. 中应变率下钢纤维混凝土受拉全过程实验研究[J]. 实验力学，2004，19(3):301-309.

[10] 胡少伟，安康. 不同尺寸混凝土三点弯曲梁试件断裂过程试验研究[J]. 水利水电技术，2015,46(6):120-125.

[11]Elices M, Rocco, Roselló C. Cohesive crack modelling of a simple concrete: Experimental and numerical results [J]. Engineering Fracture Mechanics,2009,76(10)：1398-1410.

Determination of the Trilinear Tension Softening Curve of Reinforced Concrete with Steel Fiber in Low Volumn-ratio

An Ruimei, Duan Shujin

(Civil Engineering Institute ,Shijiazhuang Tiedao University, Shijiazhuang 050043，China)

A notched three-point bent beam is researched about the tension strain softening curve that is made from reinforced concrete with steel fiber. The trilinear model is assumed for the tension softening curve. According to the tested typical value of material performance and strain distribution when the initial crack is instable, the balance equation is set up on the ligament section, and then the undetermined coefficient is solved and the strain softening curve is gotten. The result can be verified by the bent balance equation and tested strain distribution when the second strain gauge is broken. As an example, a test beam with low volume-ratio steel fiber is analyzed and the method is verified.

reinforced concrete with steel fiber;tension strain softening curve;trilinear model;equilibrium equation

2016-02-21 责任编辑:车轩玉

10.13319/j.cnki.sjztddxxbzrb.2017.01.03

河北省自然科学基金(A2015210029)；河北省高等学校科学技术研究重点项目(ZH2012040)；河北省教育厅自然科学类青年基金(QN2014062)

安蕊梅(1974-)，女，博士，副教授，硕士生导师；主要从事混凝土结构设计、施工理论的研究。E-mail: armarmarm@163.com

TU528.57

A

2095-0373(2017)01-0014-05

安蕊梅，段树金.低体积含量的钢纤维混凝土三折线拉应变软化曲线的确定[J].石家庄铁道大学学报:自然科学版,2017,30(1):14-18.