岛礁地形畸形波演化过程的试验及小波谱分析

邹丽, 王爱民， 宗智， 裴玉国, 赵勇

(1.大连理工大学 工业装备结构分析国家重点试验室,辽宁 大连 116024；2.大连理工大学船 舶工程学院,辽宁 大连 116024；3.高技术船舶与深海开发装备协同创新中心,上海 200240；4.大连海事大学 交通运输装备与海洋工程学院，辽宁 大连116026)

岛礁地形畸形波演化过程的试验及小波谱分析

邹丽, 王爱民， 宗智， 裴玉国, 赵勇

(1.大连理工大学 工业装备结构分析国家重点试验室,辽宁 大连 116024；2.大连理工大学船 舶工程学院,辽宁 大连 116024；3.高技术船舶与深海开发装备协同创新中心,上海 200240；4.大连海事大学 交通运输装备与海洋工程学院，辽宁 大连116026)

为研究某岛礁周边波浪演化过程及其特征，本文选取西太平洋的一个典型岛焦地形为研究对象，在试验水池中建立了礁地形三维模型(1∶100)。造波机输入谱为Goda改进的JONSWANP谱，谱峰升高因子γ取2.0，对不同有效波高和有效周期的定向随机波工况进行了试验。在岛礁周围布置多个浪高仪测定波浪的时间序列,并基于小波变换分析波面序列的小波谱特征。通过分析试验中的波浪演化过程，发现多个工况在地形突变处存在畸形波。通过分析小波能谱发现在畸形波近后方出现波群时，该波群会获得畸形波的能量，导致该波群的波能增大，并生成二次畸形波。试验发现地形突变会增大畸形波发生的概率。畸形波的形成与波浪的群性有关，且单次畸形波与二次畸形波演变特点存在差异。

畸形波；岛礁地形；波浪演化；小波变换；随机波；三维模型

畸形波又叫怪波或者凶波，Dean[1]建议定义波高为有义波高二倍以上的波浪为畸形波。在一些文献中也可以看到其他的有关畸形波的定义和条件[2-3]。畸形波是一个单波，具有非常大的波峰且陡峭，严重危害船只和离岸结构的安全[1,4]。由于畸形波的破坏性极强，近些年也一直是研究热点，得到了很多学者的关注和研究。波浪在变水深水域传播时，受地形变化的影响，其传播方向、大小以及剖面形状都要随传播距离而变化，当沿波峰线水深不一样时，波会生成折射，波的折射可引起波向线的汇聚或发散，从而使波能集中或分散[5]。Trulsen等通过试验研究了地形对畸形波生成概率的影响[6-7]。LI Jin-xuan等在二维试验水槽中观测了随机波中的畸形波，在BFI(Benjamin-Feir index)较大的情况下，畸形波生成的概率较大[8]。

小波分析被看成调和分析数学领域半个世纪以来的工作结晶，它在时域和频域同时具有良好的局部化特征，这也是它优于傅里叶变换的地方。在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合于探测正常信号中夹带的瞬态反常现象并展示其成分[9]。Torrence 等给出了一个小波变换的实用性指南，对小波函数、小波变换以及小波谱等做了介绍[10]。近年来，随着小波变换的不断发展与成熟，许多学者将小波变换成功应用于畸形波的研究之中，并取得了许多成果[11-13]。柳淑学等利用小波变换，对随机波浪中的二维畸形波的群效应进行了研究，发现畸形波的生成与群效应有关，是高频波群追赶低频波群的结果[14]。Cihan-Bayndr利用小波变换对畸形波进行了早期诊断研究，他发现小波谱不仅能在畸形波初期进行识别，而且可以得到时间-空间位置[15]。

探索海洋的畸形波，最困难的是缺乏实际海况测量的畸形波数据。本文基于某岛礁实际地形的三维模型试验，对试验的各个工况波浪演化过程进行分析，意外发现了畸形波的存在。我们根据试验结果，基于小波变换研究了畸形波的演化过程。值得注意的是，本试验中波浪演化是在实际岛礁模型中进行的，且畸形波并不是人为预设生成的，符合实际海况。因此本文研究具有重要的实际意义。

1 试验简介

1.1 试验模型

本试验是在大连理工大学海岸和近海工程国家重点试验室的多功能综合水池中完成，该水池有效使用尺度为55 m×34 m×0.7 m。水池一端安装液压伺服造波机，有70块造波板，另一端设有消波设施以减少波浪反射(如图1)。

所研究的岛礁位于中国周边某海域，长700 m，宽300 m，面积约为0.21 km2，高度为6.4 m。岛的一侧海床延伸几十米后水深急剧加大，另一侧为泻湖，水深较浅且变化缓慢。试验采用1∶100的比例建造该地形，其中包括岛体以及其周围陡坡、部分泻湖地形。

试验在岛礁周围共布置了50个浪高仪，记录各个工况下波高以及波浪周期，以测量波浪的整个演化过程，具体布置点如图2。

图1 多功能综合水池及岛礁模型Fig.1 Multi-function integrated basin and model of the reef

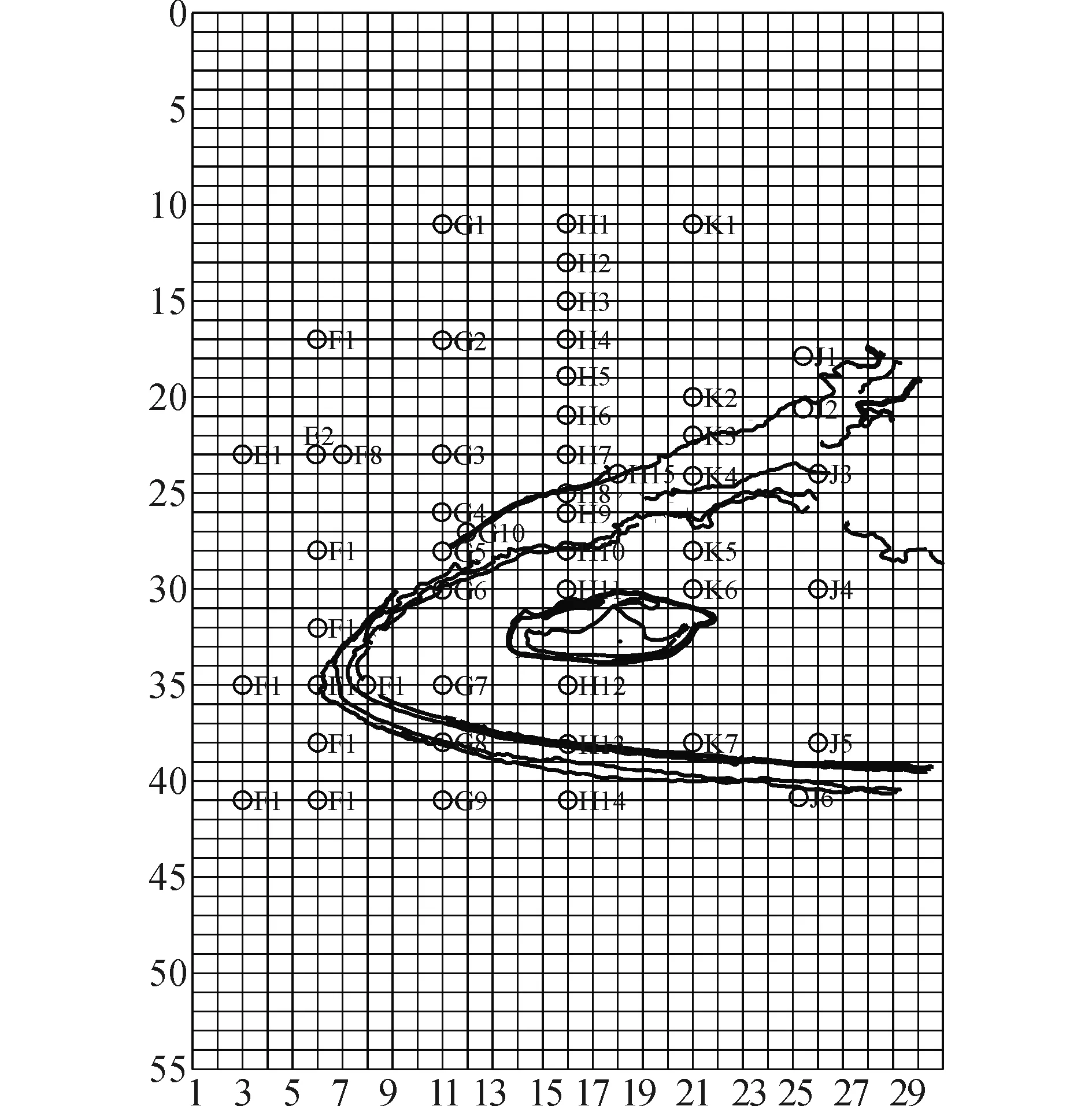
图2 试验地形及浪高仪布置图Fig.2 Test terrain and arrangement of wave height meter

1.2 试验波浪参数

模型安装前，在预设模型中心点设置浪高仪，将按模型比尺换算后的特征波要素输入计算机，生成造波信号，控制造波机生成相应的不规则波序列。经数次迭代修正后得到模型设计确定的波浪要素。

波浪模拟采用不规则波进行，选择国际上公认的JONSWAP谱进行模拟。

合田改进的JONSWAP谱可描述为[16]

(1)

(2)

(3)

(4)

式中：Hs为有效波高；Tp为谱峰值周期；fp为谱峰值频率，谱峰升高因子γ取2.0。

表1 不规则波试验工况(波浪模型参数39个工况)

Table 1 Working conditions of irregular wave test (39 cases) wave model parameters

试验共进行了39个不规则波工况的测量，统计了在多个造波工况(不同波高、不同浪向、不同周期)下岛礁周边不同地点的时历浪高数据(如表1)。试验中，在正确布置、精确测量、重复性良好的前提下，每个工况重复三遍，以排除试验的偶然性，采样时间为81.92 s，采样频率为50 Hz。

2 结果分析与讨论

2.1 畸形波存在的典型工况

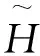
图3为波浪演化产生畸形波的两个典型工况的波面时间序列。图3(a)为造波机有义波高为6.35 cm，有义周期Ts=0.87 s时波浪演化波面时间序列。由图3(a)可以看出，在距造波机17 m，浪高仪H4处，34 s时观测到一个明显的畸形波。图3(b)为有义波高Hs=8.05 cm，有义周期Ts=0.8 s时波浪演化波面时间序列。由图3(b)看以看出，在距造波机13 m，浪高仪H2处，3 s时观测到一个畸形波波形；在距造波机17 m，浪高仪H4处，18 s时观测到一个二次畸形波波形。

2.2 地形对畸形波生成的影响

图4中选取存在畸形波的工况次数作为样本容量。由图4可以看出浪高仪H2、H4和H6处有畸形波出现。浪高仪H6，位于距离造波机21 m，水深为0.293 5 m，畸形波生成的概率也有一个突然的增加，且该位置为出现畸形波概率最大的位置。当距离造波机的距离大于25 m时，水深变浅，成为浅水区，波浪发生破碎，波能衰减，没有出现畸形波。岛礁后方波浪为绕射生成，波高较小，波能相应较小，难以形成能量集中的畸形波。并且由上图我们可以明显的看出，地形对波浪演化生成畸形波有很大的影响。

在浪高仪H6前方1 m处，即距离造波机20 m处的位置水深也变浅，该处水深为0.163 m，变化较大。由此可知地形水深突然变浅，增大了畸形波形成的概率。这与Trulsen等关于试验室中非均匀水深引起畸形波结论[6]及Gramstad等研究的浅水中底部有坡度对畸形波的影响的结果[7]相似。经过验算，水深为0.163 m时：

(5)

式中：h为水深，λ为波长。

此时为有限水深。因此本试验表明当波场在有限水深中传播时，非线性的底部同样大大增加了畸形波生成的可能性。因此应避免在H6点作业，船只航行时也应尽力避开这个位置。

2.3 基于小波变换对试验中波浪演化过程分析

本文选取了图3所示的试验工况的波浪演化过程，利用小波变换分析了畸形波形成前后，及生成畸形波时的特征，并对试验中生成二次畸形波的原因进行了分析。

表2 波浪演化过程产生畸形波的工况

图3 试验中浪演化的波面时间序列图Fig.3 Waves evolution of time series in the experiment

图4 波浪演化过程生成畸形波与地形的关系Fig.4 The relationship between freak wave produced evolution process of wave and terrain

2.3.1 波浪演化生成畸形波前后小波谱分析

为了更加清晰的观察到畸形波形成前后小波谱的特征，对图3(a)，取H2到H6浪高仪的波面高程做局部小波能谱分析，如图5所示。

由图5可以看出，畸形波形成前，在距离造波机13 m处，H2浪高仪的时间序列小波谱能量集中度不高，小波谱在25～32 s段有三个波群，具有相对较高频率的波群在具有相对较低频率的波群前。由H2～H3的小波能谱可以看出，低频波群传播快，在传播到浪高仪H3时追赶上了高频波群，波浪传播到距离造波机15 m处，H3浪高仪的小波谱能量集中度提高，且浪高仪时间序列小波谱能量都集中在低频阶段。在距离造波机15 m的H4处，生成了畸形波，畸形波发生时，小波谱能量等值线呈现近似三角形形态，在时域小波谱能量集中，且成对称分布。这与黄玉新等基于小波变换对畸形波的时频特性的研究结论相似[12]。在距离造波机17 m的H5处畸形波消失，由小波谱看出，波群解调，低频波群在波群前，这与柳淑学等研究结果相似[14]。波浪的群特性与畸形波的关系在实际岛礁地形模型试验中得到验证。

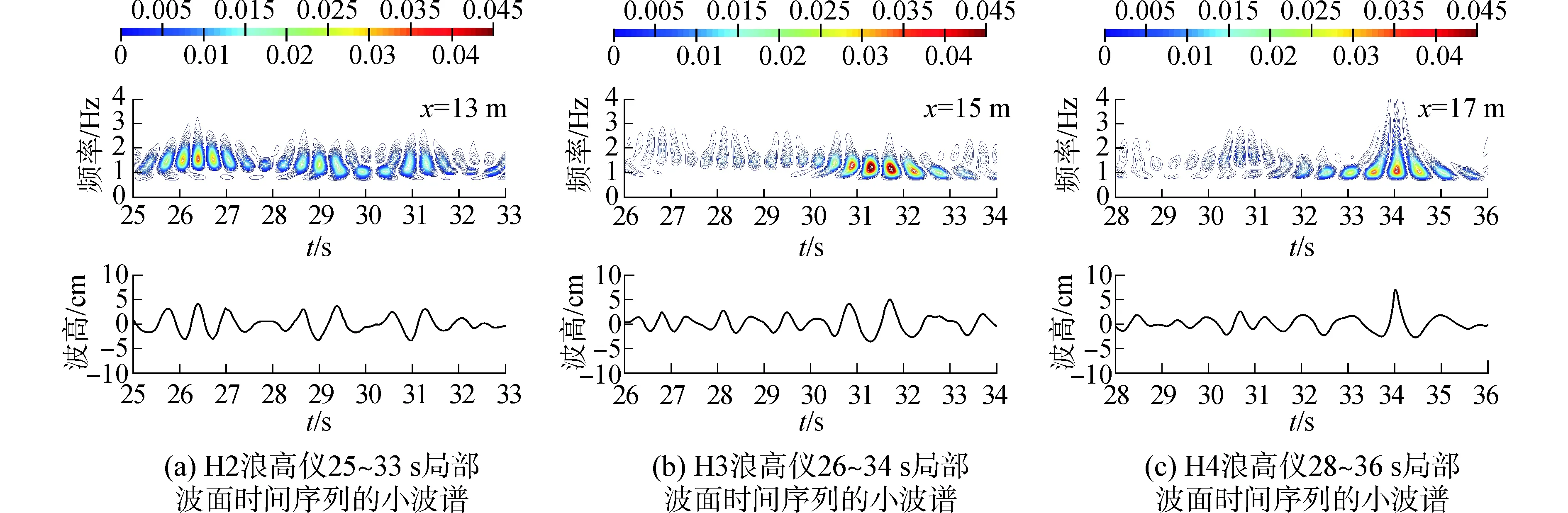
图5 Hs=6.35 cm， Ts=0.87工况时，H2～H6浪高仪局部波面时间序列的小波能谱 Fig.5 Wavelet energy spectrum of local wave time series of wave height meters H2～H6 for Hs =6.35 cm, Ts=0.87 s

虽然畸形波出现时能量集中。但是，这种集中是时域的集中，在频域上，能量集中度降低，低频能量减少，向高频转移。从浪高仪H3～H6波面时间序列的小波谱序列可以看出，这种转移是持续的，畸形波消失后，低频部分小波谱能量持续降低，高频部分小波谱能量耗散。

2.3.2 波浪演化生成二次畸形波的小波谱分析

图6表示的是浪高仪H2～H7局部小波谱。清晰的看到，第一次畸形波生成在距离造波机13 m的H2处，3 s左右时间；第二次畸形波生成在距离造波机23 m的H7处，18 s左右时间。二次畸形波生成时，前后两次畸形波的小波谱特性与上文提到的畸形波小波谱特性基本相似。小波谱等值线呈现近似三角形形态，在时间序列上小波谱能量集中。但是在能量分布上存在区别，图5中，浪高仪H4处单次畸形波小波谱呈对称分布。而图6中，二次畸形波的第一次畸形波的能量集中在前半部分，而第二次畸形波的能量集中在后半部分。第一次畸形波消失后没有演化成大波谷，畸形波波能转移到其前方的波群中。

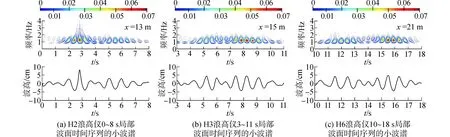
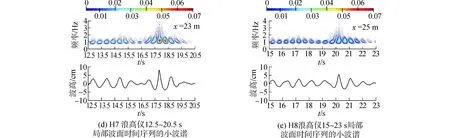
图6 Hs=8.05 cm，Ts=0.8 s 工况时，H2～H3，H6～H8浪高仪局部波面时间序列的小波谱Fig.6 Wavelet energy spectrum of local wave time series of wave height meters H2～H3 and H6～H8 for Hs=8.05 cm，Ts=0.8 s

由图6可以看出，H2处0～7 s时间段有两个波群，具有畸形波特性的波群在前。它们传播到H3时，具有畸形波特性波群的畸形波特性消失，小波谱能量降低。但是这种现象不是从低频转移到高频，而是波群之间的能量传递。从H2和H3时间序列小波谱可以明显的看到，两个波群小波谱能量和变化不大，具有畸形波特性波群后的波群小波谱能量增大，这说明能量是从具有畸形波特性波群传递到了其后的另一个波群。另外，小波谱能量在时间序列上的集中度有所降低，在频率上的集中度增加。而且在畸形波消失后，小波谱的解变质现象没有发生，这与柳淑学等研究结果不同[14]。第一次畸形波生成后，小波谱能量不再是从低频转移到高频，然后消失，这一点与前文提到的单次畸形波生成后现象不同。

波浪演化生成第二次畸形波前，没有出现高低频两个波群追赶现象，从浪高仪H6～H7波面时间序列的小波谱来看，第二次畸形波生成的原因是能量在时域的集中，有一小部分低频能量向高频转化，这与上文波浪演化生成单次畸形波是不同的。从浪高仪H8波面时间序列的小波谱可以看出，二次畸形波消失后，低频部分小波谱能量持续降低，高频部分小波谱能量耗散消失。但是小波谱没有出现波群解调，低频波群在波群前的现象。从波高来看，波高两次畸形波的波高大部分集中在水平面以上，且两次波高的高度相差仅为7.8%，说明第二次畸形波危害性依然很大。

3 结论

1)本文在对某实际岛礁地形的随机波浪演化试验中，发现波浪演化的过程中产生了畸形波。试验中波浪演化生成的畸形波，与试验室预设生成畸形波进行研究是不同的。目前，还没有在实际岛礁地形中对畸形波进行试验研究的文献报道。因此，本文的研究更符合实际情况，更具有实际意义。

2)有限水深情况下，地形对畸形波的生成有很大影响，地形突然的非线性变化，会增加畸形波生成的概率。这是Gramstad等研究的，在浅水中底部有坡度时，对畸形波影响的结果在有限水深中的推广。

3)单次畸形波生成是低频波群追赶高频波群生成的，与文献[14]研究结果相似。对于二次畸形波，其第二次畸形波的生成是能量在时域上的集中，部分能量向高频转移的结果。演化生成二次畸形波时，其第一次畸形波消失后波能从具有畸形波特性波群大部分转移到了另一个波群，这是二次畸形波成因的新特征。第二次畸形波消失后，低频部分小波谱能量持续降低，高频部分小波谱能量耗散消失，没有出现的波群解调现象。二次畸形波的前后两次畸形波都具有波峰尖瘦、能量集中的特点，由此可见其破坏力也会相当。

[1]DEAN R G. Freak waves: a possible explanation[M]//TØRUM A, GUDMESTAD O T. Water Wave Kinematics. Netherlands: Springer, 1990: 609-612.

[2]SOARES C G, CHERNEVA Z, ANTO E M. Characteristics of abnormal waves in North Sea storm sea states[J]. Applied ocean research, 2003, 25(6): 337-344.

[3]KHARIF C, PELINOVSKY E, SLUNYAEV A. Rogue waves in the ocean[M]. Berlin Heidelberg: Springer-Verlag, 2009: 2-8.

[4]MORI N, LIU P C, YASUDA T. Analysis of freak wave measurements in the Sea of Japan[J]. Ocean engineering, 2002, 29(11): 1399-1414.

[5]邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005: 231-241. ZOU Zhili. Water wave theories and their applications[M]. Beijing: Science Press, 2005: 231-241.

[6]TRULSEN K, ZENG H, GRAMSTA O. Laboratory evidence of freak waves provoked by non-uniform bathymetry[J]. Physics of fluids, 2012, 24(9): 097101.

[7]GRAMSTAD O, ZENG H, TRULSEN K, et al. Freak waves in weakly nonlinear unidirectional wave trains over a sloping bottom in shallow water[J]. Physics of fluids, 2013, 25(12): 122103.

[8]LI Jinxuan, LI Pengfei, LIU Shuxue. Observations of freak waves in random wave field in 2D experimental wave flume[J]. China ocean engineering, 2013, 27(5): 659-670.

[9]胡昌华, 李国华, 周涛. 基于MATLAB 7.x的系统分析与设计—小波分析[M]. 3版. 西安: 西安电子科技大学出版社, 2008: 1-7.

[10]TORRENCE C, COMPO G P. A practical guide to wavelet analysis[J]. Bulletin of the American meteorological society, 1998, 79(1): 61-78.

[11]KWON S H, LEE H S, KIM C H. Wavelet transform based coherence analysis of freak wave and its impact[J]. Ocean engineering, 2005, 32(13): 1572-1589.

[12]黄玉新, 裴玉国, 张宁川. 基于小波变换的畸形波生成过程时频特性研究[J]. 水动力学研究与进展, 2009, 24(6): 754-760. HUANG Yuxin, PEI Yuguo, ZHANG Ningchuan. Time-frequency characteristics analysis of generating process of freak waves based on wavelet transform[J]. Chinese journal of hydrodynamics, 2009, 24(6): 754-760.

[13]VELTCHEVA A, SOARES C G. Wavelet analysis of non-stationary sea waves during Hurricane Camille[J]. Ocean engineering, 2015, 95: 166-174.

[14]LI Jinxuan, YANG Jiqing, LIU Shuxue, et al. Wave groupiness analysis of the process of 2D freak wave generation in random wave trains[J]. Ocean engineering, 2015, 104: 480-488.

[15]BAYINDIR C. Early detection of rogue waves by the wavelet transforms[J]. Physics letters A, 2016, 380(1/2): 156-161.

[16]俞聿修, 柳淑学. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2011: 149-150. YU Yuxiu, LIU Shuxue. Random wave and its applications to engineering [M]. Dalian: Dalian University of Technology Press, 2011: 149-150.

Experiment and wavelet analysis of the evolution process of freak waves around reefs

ZOU Li1,2,3, WANG Aimin2, ZONG Zhi2,3, PEI Yuguo2, ZHAO Yong4

(1. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China; 2. School of Naval Architecture, Dalian University of Technology, Dalian 116024, China; 3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China; 4. Transportation Equipment and Ocean Engineering College, Dalian Maritime University, Dalian 116026, China)

To study the evolution process and the characteristics of waves around some reefs, the terrain of a typical reef in the western Pacific was chosen as the research object in this paper. The three-dimensional model on the reef terrain (1∶100) was set up in the test tank. The Goda-improved JONSWAP spectrum was applied as the input of a wave maker, with the spectral peak elevation factorγequalto2.0.Thebehaviorsofthedirectedrandomwavewithvarioussignificantperiodsandwaveheightsweretested.Manywavegaugeswerelaidoutaroundthereef.Inaddition,thecharacteristicsofthewaveletspectrumofthewavesurfacesequenceswereanalyzedonthebasisofthewavelettransform.Byanalyzingtheevolutionprocessofwavesinthetest,itwasfoundthatfreakwavesexistattheterrainbreakundermanybehaviors.Byanalysisofthewaveletenergyspectrum,whenawavegroupappearsnearthebackoffreakwaves,thewavegroupgetstheenergyofthefreakwave,andtheenergyofthewavegroupincreases;inaddition,secondaryfreakwavescouldform.Also,theterrainmutationcouldresultinahighprobabilityoffreakwaves.Thegenerationoffreakwaveshasacertainrelationshipwiththefeaturesofthewavegroup;inaddition,theevolutioncharacteristicsofsinglefreakwavesandsecondaryfreakwavesaredifferent.

freak waves; reef terrain; wave evolution; wavelet transform; random wave; three-dimensional model

2016-03-29.

日期：2017-03-03.

国家重点基础研究发展计划 ( 2013CB036101)；国家自然科学基金项目 ( 51379033，51522902).

邹丽(1981-)，女，教授，博士生导师； 宗智(1964-)，男，教授，博士生导师.

邹丽,E-mail:lizou@dlut.edu.cn.

10.11990/jheu.201602007

P731.22

A

1006-7043(2017)03-0344-07

邹丽, 王爱民， 宗智，等.岛礁地形畸形波演化过程的试验及小波谱分析[J]. 哈尔滨工程大学学报, 2017, 38(3):344-350.

ZOU Li, WANG Aimin, ZONG Zhi，et al.Experiment and wavelet analysis of the evolution process of freak waves around reefs[J]. Journal of Harbin Engineering University, 2017, 38(3):344-350.

网络出版地址：http://kns.cnki.net/kcms/detail/23.1390.U.20170306.1359.002.html