电抗器铁芯振动噪声多物理场研究

刘骥　何亚倩　李凯

摘要：在磁致伸缩和麦克斯韦方程相关理论研究的基础上，采用有限元方法利用有限元软件COMSOL，在瞬态电磁场耦合、结构力场耦合以及声场耦合基础上建立了一台三相串联铁芯电抗器模型，针对三相串联铁芯电抗器在工频工作状态下的磁场分布、铁芯磁致伸缩位移、铁饼间的麦克斯韦力位移和声压级进行分析研究。根据仿真中电抗器的瞬态磁场分布，得到电抗器内部磁通密度分布、振动位移分布，进而得到声场分布。实验表明，多物理场仿真得到的结果与实测数据基本一致，证实运用多物理场耦合对噪声进行预估是一种有效的方法。

关键词：铁芯电抗器；噪声；磁致伸缩；有限元

中图分类号：TM477 文献标志码：A 文章编号：1007-2683（2017）01-0035-06

0 引言

铁芯电抗器作为在电力系统中不可缺少的基础设备之一，具有漏磁小、节省空间等优点。随着城市中新能源和配电系统飞速发展，电抗器已经广泛使用在城市。与此同时铁芯电抗器运行中产生的振动噪声严重污染周边环境，此外电抗器在运行过程中的振动噪声过大对电抗器安全运行也会构成威胁。电抗器铁芯结构中存在气隙，导致电抗器的振动噪声问题比同容量电力变压器更加严重，针对铁芯电抗器振动噪声的分析研究与控制的问题急需解决。

目前，针对电抗器振动噪声的研究一般是依据实际测量到电抗器振动噪声数据对现有电抗器结构加以改进，并没有在设计电抗器结构模型环节中考虑其引起的振动噪声问题，因此并没有电抗器模型所引起的振动噪声的定量参数。国内外关于铁芯电抗器和变压器的研究一般集中在测试技术与电磁计算分析模块。魏亚军针对三相电力变压器建立多物理场二维模型研究振动噪声，研究分析了在空载和负载两种情况下的铁芯振动和绕组振动，提出在负载情况下的绕组振动不可忽视。汪金刚等针对直流偏磁情况下电力变压器振动进行了理论分析仿真，并验证了模型建立的可靠性。周金标等分析了串联电抗器运行中的异常噪声。刘旺玉等利用ANSYS软件研究分析了干式串联电抗器振动噪声，并提出降噪措施。孙国志等针对变电站电抗器噪声进行了测试、分析和研究。

本文利用有限元软件COMSOL在瞬态电磁场耦合、结构力场耦合以及声场耦合基础上建立一台三相干式串联铁芯电抗器模型。本文主要研究在磁致伸缩效应和麦克斯韦力作用下的电抗器振动噪声问题，不考虑绕组以及其他元件的振动，针对电抗器铁芯的振动位移以及噪声进行分析，得到电抗器铁芯的振动位移与噪声分布，并与实际测量到的數据进行对比。

1 模型建立及多物理场耦合原理

1.1 模型建立

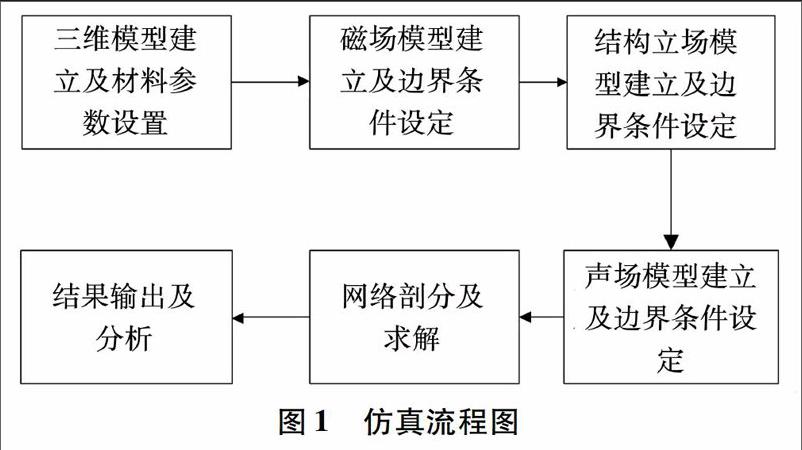
本文选用有限元软件COMSOL对电抗器进行仿真分析，有限元仿真过程如图1所示。

建立三维模型，考虑到网格过密导致计算时间过长或不收敛，将铁芯简化为由一块硅钢片构成；考虑铁芯结构对涡流的抑制作用，适当减小铁芯材料的电导率；考虑到结构件对铁芯夹紧力作用，设置上下面为固定约束，即振动位移为零。简化模型如图2所示：

其中铁心电抗器主要参数如表1所示：

设置铁心、绕组、气隙和空气材料参数如表2所示。

1.2 多物理场耦合

电抗器在正常工作状态下，电抗器绕组电流在铁芯构成的磁体中产生交变的磁场，其中磁场微分方程为：

（1）其中μ₀为真空磁导率，其值为4π×10^-7H/m，μ^r为相对磁导率，A为矢量函数磁矢位。

将软件计算得到电抗器磁体中的磁感应强度B、磁场强度H以及M代入到求解域方程中，以实现磁场和结构力场的耦合。建立方程如下：

（2）其中m为质量矩阵，三为阻尼系数矩阵，K为刚度矩阵，u为位移向量。

将铁芯中计算得出的磁致伸缩和麦克斯韦力与结构力场进行耦合，其中磁致伸缩线性弹性方程为：

▽·σ=-F_V （3）式中，σ为应力张量，F_V为体积力。

将磁致伸缩力设定为电抗器铁芯初始应变参数，其中磁致伸缩力是在任何方向都可以磁化的函数，其中方程可表示为：

（4）

将麦克斯韦力设定为电抗器铁芯初始应变参数，其中电抗器铁芯中存在气隙，在任何时刻相邻铁芯都是异性磁极，因此相邻铁芯中麦克斯韦力为吸引力，其方程为：

（5）

在结构力场模块中计算得到铁芯体积应变，并将其带作为振动初始值代入到铁芯中，在铁芯振动所产生的声音传播到空气域，实现了结构力场与声场的耦合。其中微分方程如下：

（6）式中，ρ₀为空气密度，p为声压，q为偶极源，Q为单极源。

2 仿真结果与分析

2.1 铁芯中磁通密度分布与气隙关系

设定电抗器三相绕组额定电流分别为：

（7）

与变压器铁芯不同，电抗器铁芯存在气隙，气隙的存在使得电抗器的漏磁远远大于同容量同电压的变压器的漏磁，因此电抗器的振动噪声问题比变压器更加严重。仿真可以得到，t=0.005 s中铁芯中磁通密度的分布如图3所示：

由式（9）可以得出t=0.005 s时B相电流达到最大值。由图3可知，t=0.005 s铁芯中柱磁通密度最大，在铁芯拐角和气隙处可以看出磁通密度集中现象，气隙是电抗器振动噪声问题的主要原因。

2.2 加载不同载荷下的振动噪声分析

磁致伸缩效应是指磁体在被外磁场磁化时，其体积和长度将发生变化的现象，由于体积变化微小，本文只研究线磁致伸缩效应。铁芯中各个方向的振动与各个方向磁致伸缩力有关，而磁致伸缩力与铁芯中的磁通量相关。单在磁致伸缩载荷作用下的铁芯位移如图4所示。

由于仿真中对铁轭的上下两面设定为固定约束，因此对中柱的振动位移起到一定限制作用，而对两侧铁芯柱的振动位移量并没有产生很大影响。

对铁芯只施加麦克斯韦力时铁芯位移分布如图5所示。

由图4、图5可以验证得知铁芯的位移分布与磁通密度的分布密切相关，而且可以看出铁芯在气隙处的振动比较大，这是由于电抗器铁芯存在气隙导致漏磁增大，因而使得气隙处的振动比其他结构处的更加明显。由磁致伸缩力与麦克斯韦力引起的振动位移相差两个数量级。磁致伸缩引起的铁芯振动位移远远大于麦克斯韦力。

如图6所示为只有磁致伸缩载荷作用下的铁芯振动噪声声压级分布。在麦克斯韦载荷作用下产生的铁芯振动所引起的噪声声压级分布如图7所示。

由图6、图7比较可得，磁致伸缩效应所产生的振动噪声远远大于麦克斯韦力作用下的，电抗器铁芯的振动噪声是由磁致伸缩效应作用产生的，麦克斯韦力作用下的电抗器振动噪声很小。

2.3 线圈电流与振动噪声关系

对绕组施加電流分别为30 A、40 A、50 A、60 A时，分析磁场分布、振动位移分布和声场分布。

为了对铁心和绕组中的磁通密度分布进行深入分析，分别选取铁心柱A、B、C中点位置截点，得到电抗器铁芯的磁通密度、振动位移以及声压随激励电流的变化分别为图8、图9、图10所示。

由图8可知，不同电流下的铁心磁通密度分布不同，随着电流增大，铁心的磁通密度逐渐增大；由图9可知，随着电流增大，电抗器的振动位移增大；由图10可知，随着激励电流的增大，电抗器噪声声压级逐渐增大。

2.4 铁芯内部位移变化

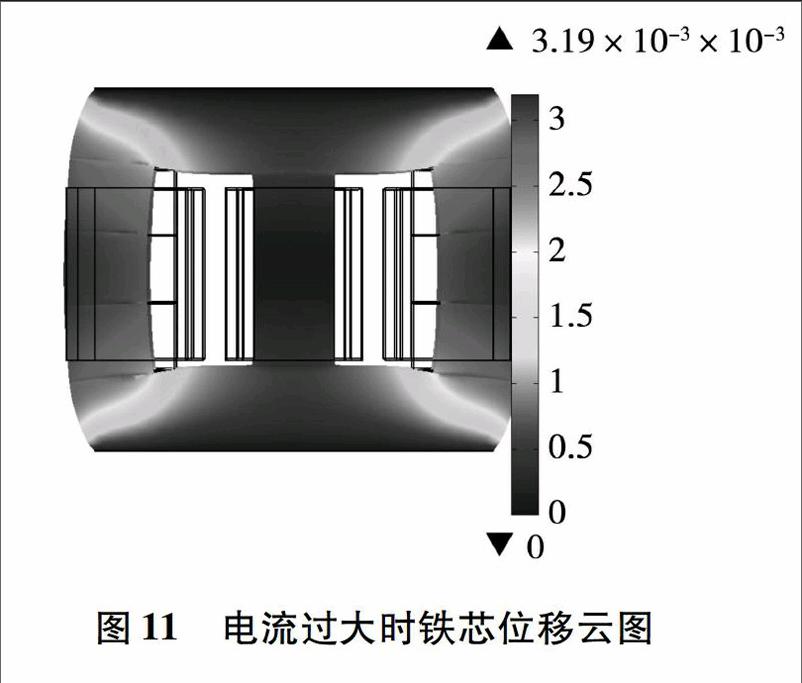
随着绕组电流的增大，铁芯的振动位移越来越大，加大绕组线圈电流就能看到明显的铁芯振动位移变化，如下图11所示：

考虑到结构件对铁芯夹紧力作用，设置上下面为固定约束，即振动位移为零，所以对铁心中柱的位移有明显的抑制作用。可以看出两侧铁芯内部振动位移与表面一致，都是向外侧拉伸变形。

3 实验验证

本文利用DT-8852专业高精度采样分析电抗器噪声声级以求证仿真实验的可靠性，声压级的计算精度为±0.1 dB。分别在距离铁芯15 cm和30 cm处选择一点检测三相串联铁芯电抗器噪声声压级，如下图12所示。记录下来的实测噪声与仿真结果相对比，如下表3所示。

将数据对比可知，实际测到的噪声数据与仿真结果基本相符合，误差在工程允许范围内。且由于空气阻抗等原因使声音在传播中能量逐渐减小，因此30 em处检测到的声压级相对15 cm处的声压级小，与实际情况相符合。

4 结论

本文利用COMSOL有限元软件通过多物理场耦合方法分析电抗器铁芯振动噪声，得到以下结论：

1）磁致伸缩效应和麦克斯韦力造成电抗器振动主要集中在铁芯气隙处，所以气隙是造成电抗器振动噪声的主要原因。与变压器相比，变压器铁心没有气隙，因此电抗器的噪音要大得多。

2）磁致伸缩效应远大于麦克斯韦力导致铁芯振动的作用，且相差两个数量级，铁芯振动主要是磁致伸缩效应产生的，且集中在气隙处。

3）随激励电流逐渐增大，铁心中磁通体密度逐渐增大，电抗器振动逐渐增大，从而使电抗器振动噪声增大。

4）电抗器铁芯内部位移与表面位移一致，向外侧拉伸变形。

由于磁致伸缩效应和麦克斯韦力作用，电抗器铁芯在运行过程中会产生振动引发噪声，此外绕组的振动与其他结构件元件的振动也引起了一定量的噪声，今后也可以利用有限元软件通过多物理场耦合的方法分析绕组以及其他元件所导致的振动噪声问题。

（编辑：关毅）