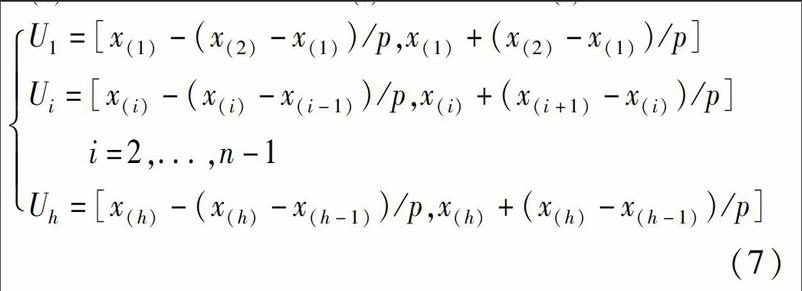小样本情况下参数区间估计的改进方法

孙慧玲　胡伟文　刘海涛

摘要：小样本情况下实验数据的概率分布较难确定，传统小样本估计方法无法提供准确的参数估计；针对工程上常用的Bayes Bootstrap方法对小样本可靠性参数估计仅仅是原样本的重复，在参数区间估计上精度不够高的问题；在不改变原样本数据的基础上，依据时间序列将原样本分组并扩充，对扩充后的样本进行参数点估计和区间估计，提出针对小样本情况下参数区间估计的改进方法，给出了改进方法的算法。运用蒙特卡罗仿真方法进行建模仿真，结合具体算例分析，验证新方法对小样本情况下参数的区间估计精度有显著提高。

关键词：小样本；Bayes Bootstrap方法；区间估计

中图分类号：0211 文献标志码：A 文章编号：1007-2683（2017）01-0109-05

0 引言

样本容量n≤30在工程上一般被认为是小样本.如果是正态分布，小样本的样本量界定可能更小，甚至小于10。随着高新技术在武器系统中的广泛应用，武器装备是否能保证每次成功完成任务与其可靠性直接相关，因此，可靠性是衡量装备性能的一个重要指标；导致在研制武器装备的过程中，其精度及可靠度要求越来越高；使得技术更复杂，造价更昂贵成为整个研制系统的大趋势。特别是某些破坏性试验，一次实验往往要付出巨大的代价。针对这类试验的传统鉴定方法已不再适用。因为传统鉴定方法是以经典统计理论为基础的，也就意味着较大的样本量必不可少，而昂贵的武器装备从安全以及节约的方向考虑，显然不适合进行大量试验。

从统计学角度分析，武器装备的可靠性研究是参数估计的范畴，是参数估计的具体实例。目前，工程上已经积累了不少方法来处理小样本问题，根据有无先验信息这点进行界定，它们大致可以被分为两大类：一类是以Bayes方法为代表的传统估计方法。该方法仅利用原始积累实验数据也即历史信息来估计参数。另一类是以Bootstrap和BayesBootstrap方法为代表的方法。该方法仅仅利用当前实验数据，在样本量较小的情况下，可以对参数进行比较准确的估计。

本文先介绍Bayes Bootstrap方法的基本思想和基本步骤；随后分析该方法的不足之处，针对不足提出改进意见；最后通过具体算例验证改进方法的可行性。

1 小样本参数估计Bayes Bootstrap方法

1.1 Bayes Bootstrap方法的基本步骤

定义1 观测样本X=（x₁，x₂，…，x_n）为总体样本，其样本量是有限的，称该样本为原生样本，设x_i～F（x），i=1，2，…，n，F（x）未知，则这些原生样本构造的经验分布函数为

（1）式中：x_（1）≤x_（2）≤…≤x_（n）是顺序统计量，是按x₁，x₂，…，x_n从小到大的排序后得到的。

步骤1：假设θ=θ（F）是总体的某个参数（例如均值或方差），θ=θ（F_n）是总体参数θ的估计值，记：

1.3 Bayes Bootstrap方法的分析

根据1.1的介绍可知Bayes Bootstrap方法没有添加任何样本以外的信息，仅仅是在原样本的基础上的重复抽样，对样本点进行了一定的修正，并且扩大了样本容量对原有参数进行估计。据已有的成果，小样本情况下（样本量为10），Bayes Boot-strap方法明显优于经典统计法，不仅在参数点估计更接近真实值，并且得到的估计置信区间更短。

研究中发现，Bayes Bootstrap方法对Dirichlet分布和原生样本依赖性较大。另外，Bayes Boot-strap方法的再生样本是取自Dirichlet分布随机数与原样本的加权平均，在（0，1）区间生成一序列的随机数结果有多种可能，一旦生成的随机数均匀性不好就会导致实验结果出现很大差别。鉴于以上局限性，有专家学者对Bayes Bootstrap方法提出了改进意见，一是对经验函数提出改进意见，重新构造更为合理的经验分布函数；二是对小样本的Boot-strap抽样方法进行改进，目的在于调整抽样方法，增大样本容量。在具体工程问题中，这些改进方法都有较好的适应性。

3 算例

前面介绍了小样本参数估计的传统方法和Bayes Bootstrap方法，本文提出了基于Bayes Boot-strap方法的改进意见并给出了仿真流程，下面通过具体实例来比较3种方法在实际问题中的适应性，验证改进方法的优越性。

例计算机生成服从正态分布N（2，0.5）的10个随机数1.7837，1.1672，2.0627，2.1438，1.4268，2.5955，2.5946，1.9812，2.1636，2.0873，取置信度1-α=0.95，分别用传统小样本估计方法、BayesBootstrap方法以及改进Bayes Bootstrap方法对参数μ作点估计和区间估计。

解：用传统方法计算，根据式（4）可得μ的点估计μ=2.006，μ的置信度为0.95的置信区间为[1.7388，2.2625]。由于n=10是小样本数据，考虑运用Bayes Bootstrap方法和改进Bayes Bootstrap方法对μ进行估计，方法如下：

构造并产生N=10 000组自助统计量（可以更大），根据式（5）、（6），运用Bayes Bootstrap方法得到参数μ的点估计值和区间估计（见表1），μ的参数分布如图2所示。根据改进方法增大样本容量的思想，可将原样本数据分为2组，运用式（8）、（9），改进Bayes Bootstrap方法得到μ的估計值和区间估计（见表1），μ的参数分布如图3所示。

4 改进方法的评价

鉴于原Bayes Bootstrap方法对原始数据及Dirichlet分布的依赖性较大，在样本量较小情况下很难得到满意的估计，改进方法在以下方面克服了原方法的不足：第一，先将样本按时间序列分组，在每一组中重构顺序统计量，克服了Bayes Bootstrap方法中再生样本数据向中间点集中的趋势；第二，调整了抽样方法从而扩展了样本容量，将每一组的样本容量都进行了扩充，并且将最大最小顺序统计量延拓至非观测点，极大地降低了再生样本与原样本的相似性。

5 结论

表1的数据显示，改进方法对参数μ的点估计与原方法相差不大。而在相同置信度的情况下对参数μ的区间估计精度明显比Bayes Bootstrap方法更好，原因是改进方法对样本的延拓必然增大了样本信息，从理论上讲，在置信度一定的情况下，提高区间估计精度只能依靠增加样本容量，所以，改进方法的实际建模效果与统计学原理也是一致的。

本文并未对参数σ进行估计，那么，改进方法对参数σ是否也具有良好的适应性还有待进一步研究。

（编辑：温泽宇）