探究食物网中食物链的数量

郭进宏

食物链和食物网的相关概念及数量计算，出现在人教版高中生物教材必修III中第五章第一节中。是高考必考的内容。探究食物链的数量问题，是对于食物网相关的考查首先要解决的问题，有利于学生较快把握题目的结构，准确解答相关问题，也有利于教师有效地教学。

食物链食物网数量

一、引言

随着新一轮高考改革的进行，对于学生的学习能力有了更深层次的要求，特别是对于探究能力、解决实际情况的能力的考查。探究食物链的数量，是解决有关生态系统的稳定性、物质循环、能量流动、信息传递的先决条件。在实际的教学中，因为没有相关的、系统的食物链数量的教学方法，使教师及学生在教学此问题时，往往会因为疏忽而导致食物链数量的错误，进而影响后续的解题。本课题正是结合多年的教学经验及高考的考查，总结出相关的方法。

二、探究食物链的数量

方法一：传统的路径法

以第一营养级为起点，以最高营养级为终点，注意每条路径上的分岔点。

例1.2014江苏卷。如图，食物链有8条。

食物链1：甲→乙→辛；

食物链2：甲→乙→丁→辛；

食物链3：甲→丙→乙→辛；

食物链4：甲→丙→乙→丁→辛；

食物链5：甲→丙→丁→辛；

食物链6：甲→丙→已→庚；

食物链7：戊→丁→辛；

食物链8：戊→已→庚。

方法二：树状图法

以第一营养级为起点，最高营养级为终点，每种捕食关系对应一条分支。最高营养级出现的次数即为食物链的条数。

识图可知，辛和庚作为最高营养级在食物链的结尾共出现8次，即8条食物链。

从图中，可知，同一列为同一营养级，第几列即為第几营养级。同时，可反映出，同一种生物可处于不同营养级，如辛，可处于第三、第四、第五营养级。

方法三：计算法

第一营养级：在生态系统中，生产者只会被捕食，所以可描述为只出不进，0进n出，计n；最高营养级：同理，只进不出，m进0出，计0（因为在倒数第二营养已经计算在内）；其他营养级：X进Y出；Y-1代表此路径已经被利用一次；X代表利用次数；Σ表示所有的集合求和。

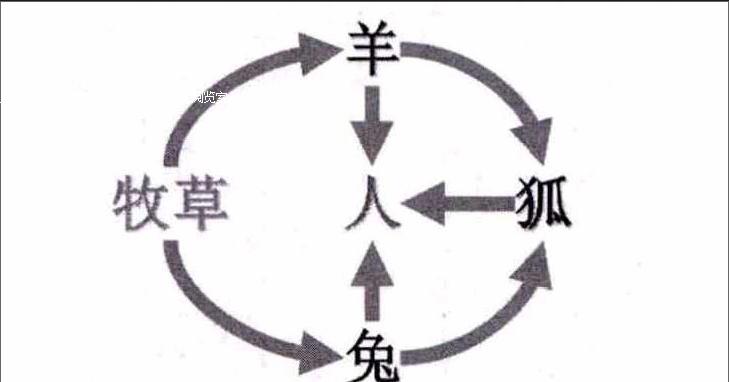
例2.2011年新课标卷。如图，食物链有4条。

如上题：第一营养级的牧草可被羊和兔食用，0进2出，计n=2；最高营养级的人，可捕食羊、兔、狐，3进0出，计0；其他营养级的羊，只能捕食牧草，但被人和狐捕食，1进2出，套用X羊（Y羊-1）=1（2-1）=1；同理，兔，X兔（Y兔-1）=1。求和：N=

对于有多个第一营养级的食物网，采用拆分法，把食物网拆分为相应数量的食物网后，分类讨论后求和。拆分的依据为：凡是和某第一营养级相关的生物，全为同一食物网。

例3.2014江苏卷改编。

由于此食物网中有两个第一营养级，且乙同时捕食两种第一营养级，对于此类食物网，必须先拆分为两个食物网进行分类讨论。

和甲相关的物种有乙、丙、丁、已、辛和庚；和戊相关的物种有乙、丁、已、辛和庚。分解为两图。

情况一：第一营养级的甲，0进2出，计2；最高营养级有辛和庚，总计3进0出，计0；其他营养级的乙，2进2出，所以X乙（Y乙-1）=2；其他营养级的丙，1进3出，所以X丙（Y丙-1）=2；其他营养级的丁，2进1出，所以X丁（Y丁-1）=0；其他营养级的乙，1进1出，所以X已（Y已-1）=0；N1=Σ{n}+Σ{X（Y-1）}=2+（2+2）=6

情况二：第一营养级有戊，0进3出，计3；最高营养级有辛和庚，总计3进0出，计0；其他营养级的乙，1进2出，所以X乙（Y乙-1）=1；其他营养级的丁，2进1出，所以X丁（Y丁-1）=0；其他营养级的已，1进1出，所以X已（Y-已1）=0；N2=Σ{n}+Σ{X（Y-1）}=3+1=4；∴N=N1+N2=10

三、解题规律

1.凡是X进1出的营养级，X（Y-1）=0。所以，在熟练之后，先确定并计算第一营养级，再排除最高营养级和X进1出的营养级。其他的逐个计算。

2.并不是所有的含有多个第一营养级的食物网都需要拆分，如上题，亦可不拆分。但为了方便学生理解和教学的深入浅出，在这里不讨论多个营养级不拆分的情况。

四、结束语

食物链的数量问题是高考的必考内容，也是学生必须要掌握和应用的能力。以上讨论的方法，有助于教师的教学和学生的学习。在实践操作中，应就每种方法进行逐一的介绍，让学生掌握每种方法的本质和内涵，进行对比，从而掌握应用。然后，根据题目要求，采用适合的方法，快速解答此类问题。

参考文献：

＼[1＼]人民教育出版社、课程教材研究所、生物课程教材研究开发中心.普通高中课程标准实验教科书·生物必修3·生态系统的结构.2016.88-92.