基于时间序列的长沙市PM2.5的统计分析

李波+朱恩文+冯倩

摘要通过对长沙市2015年AQI检测指标数值PM2.5与SO2，NO2，PM10，CO，O3间相关性进行分析，得到PM2.5与SO2，NO2，PM10，CO间存在正相关关系，与O3间为负相关关系.后建立自回归移动平均模型（ARMA）对长沙市2015年的PM2.5进行短期预测，得到最优模型为ARMA（3，2）.最后对长沙治理PM2.5提出相关建议.

关键词PM2.5；AQI ；多元回归模型； ARMA

中图分类号 O213；X501 文献标识码A

1引言

大气中的灰霾微粒对人们的身体健康带来了巨大的威胁，经有关部门监测研究发现，PM2.5是导致灰霾天气的罪魁祸首[1].长沙市环境监测部门表示，2015年11月1日至2015年12月18日的长沙市的空气质量极差，长沙市的空气质量在全国重点城市的排名为：11月份1至11月份18日排名居中，其他12天均排名为全国倒数十名之内长沙市被列入全国空气污染较严重的城市[2].

孫斌对西安市大气污染因子（可吸入颗粒物、NO2、SO2）的年际变化进行分析，并采用基于灰色系统理论和灰色预测模型的方法进行灰色关联度分析，揭示西安市大气环境质量近10年的变化趋势，还对未来的大气环境质量状况进行了预测[3].

本文首先分析PM2.5与SO2，NO③求复相关系数.经过MATLAB运行求解，得到复相关系数R=0.966 0.

通过上述分析，可以得到如下结论：PM2.5与其他5个监测指标之间均存在不同程度的显著性，PM2.5与SO2，NO2，PM10，CO间为正相关关系，与O3间的相关性为负相关.具体表现为：PM2.5与PM10的相关系数最高（高达0.743），说明PM10对PM2.5的影响最大；其次PM2.5与CO的相关系数为0.732，说明它们二者间的相关性较高；除此之外PM2.5与NO2及SO2的相关系数分别为0.688和0.618，表明PM2.5与它们二者间的也存在较大的相关性.说明已有的研究结论是存在合理性的，即二氧化硫（SO2），二氧化氮（NO2），一氧化碳（CO）是在一定环境条件下形成PM2.5前的主要气态物体；而PM2.5与O3间呈负相关关系，说明O3对于PM2.5可能有一定的抑制作用，因此保护大气中的臭氧层对于PM2.5的减少有着重要意义.

2.3PM2.5与其他指标的多元回归分析

多元回归分析可以分析一个因变量与多个自变量间相关性[7].对不同因子组合的数值进行多元统计分析，能够得到因变量与自变量的数量关系.本文针对PM2.5与其他5个因子进行多元统计分析，进而分析PM2.5与其他5个因子之间的具体数量关系.

通过上文分析发现，PM2.5与其他5个因子间存在较为显著的相关性，但直接建立PM2.5与其他5个指标的多元回归时，SO2会由于显著性检验不显著而被剔除，这与SO2与PM2.5的相关性很高相违背，为了使SO2能够更好的解释PM2.5，故需对SO2、CO等5个指标进行主成分分析，然后再建立PM2.5与主成分之间的多元回归模型.因此对SO2、CO等5个指标进行主成分分析结果见表3.

2与PM2.5成正比例关系，这与PM2.5和NO2相关性很高相一致.当主成分F1不变时，主成分F2每增加或减少一个单位，PM2.5减少或增加2.948个单位，这从侧面也反映了O3与PM2.5成反向关系，这也与PM2.5和O3相关性为负相一致.

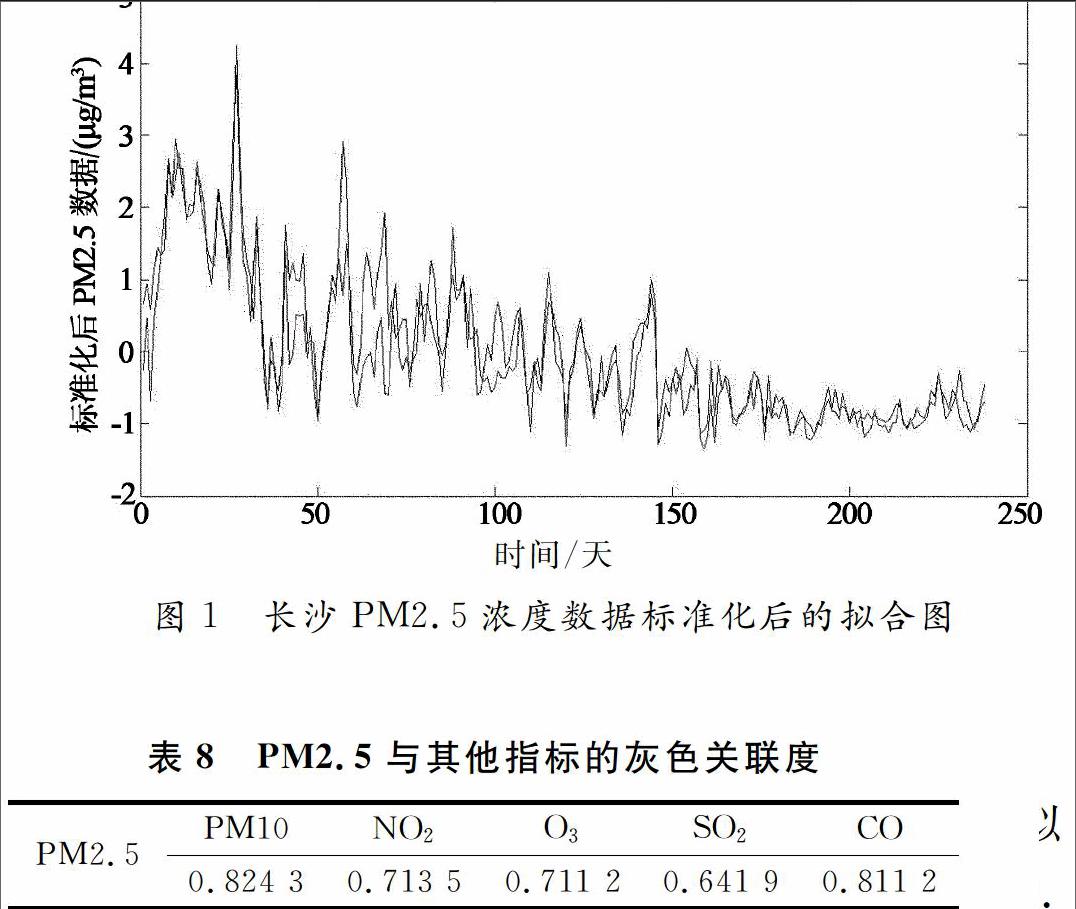
本文采用2013～2014年的AQI的相关数据[8]，用MATLAB软件对于长沙市PM2.5拟合标准化后的数据绘制成图得到图1.图1表示2015年中PM2.5浓度随时间的变化图像.观察图像可发现，PM2.5随时间变化波动较大，其中PM2.5在第一季度浓度较大，在第二、三季度的变化波动幅度较小.从一定程度上说明春节期间，长沙居民对于烟花爆竹的使用量较大，特别是橘子洲烟火节，在一定程度上对空气造成较严重的污由于防爆剂中的重金属在燃烧过程中会被吸附在含碳的颗粒物上，使得空气中PM2.5的含量更高.尽管PM2.5的波动变化不均匀，但从图形拟合效果图来看，多元回归模型拟合效果很好，这也充分说明先对指标采取主成分分析后再建立多元回归模型的合理性.

时间/天

观察表8中的数据可以发现，PM2.5与PM10的关联度最大，说明它们两者之间存在极强的相关性.也就是说PM2.5含量伴随着PM10的增加而增加、减少而减少.分析这一现象产生的原因可知，它们两者本质上属于同一种物质，仅仅由于微粒直径不同因此使得PM2.5与PM10相关性较大.这也从侧面反映了，在进行某些研究分析时，可以利用PM10的数据进行近似分析.同时，可以看出PM2.5与CO的灰色关联度为0.8112，由此可见一氧化碳对PM2.5的形成产生较大的影响；接着看出NO2的灰色关联度为0.7135，可见氮化物对PM2.5的浓度变化也存在相当大的影响；再次O3的灰色关联度为0.7112，说明O3对PM2.5也是有一定关系；最后看到PM2.5与SO2的灰色关联度为0.641 9，通过此种方法得出CO与PM2.5的灰色关联度比较低.

综上所述，采用灰色关联分析的方法可以看出，PM2.5与PM10的关联度最大，与SO2的关联度最小.从一定程度上说明了PM2.5的形成主要是由于氮类化合物以及硫化物.但总体来说，PM2.5与这5个因子之间存在较强的相关性.

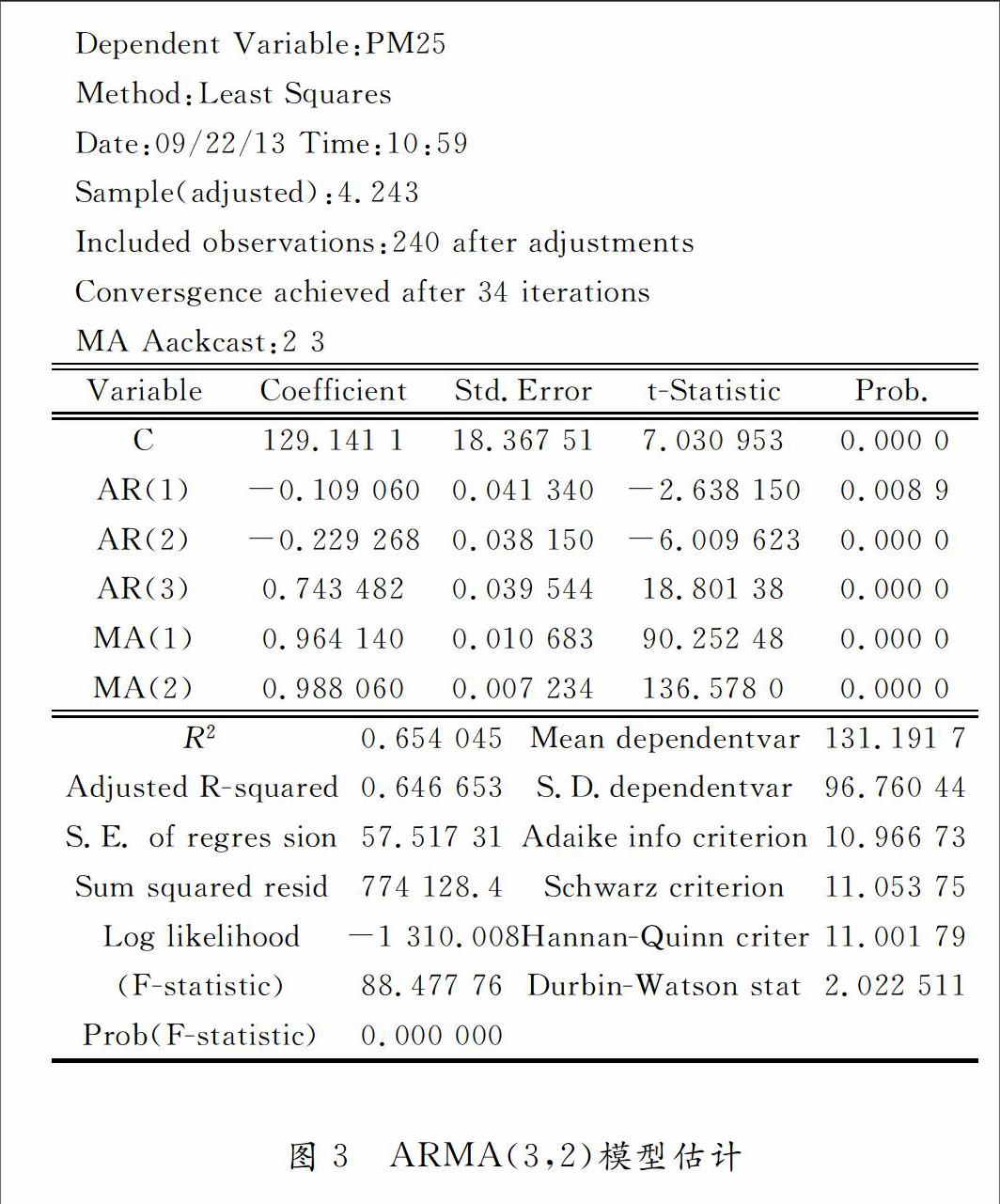
3PM2.5的预测模型

本章节通过对长沙地区2015年期间的PM2.5的数据进行统计分析，采用时间序列预测分析的方法，建立了自回归移动平均模型（ARMA）对PM2.5数值进行短期预测.经分析后发现，ARMA模型对PM2.5浓度的波动变化拟合效果较好，除此之外也有较强的短期预测效果.

3.1PM2.5时间序列分析模型建立

3.1.1时间序列模型简介

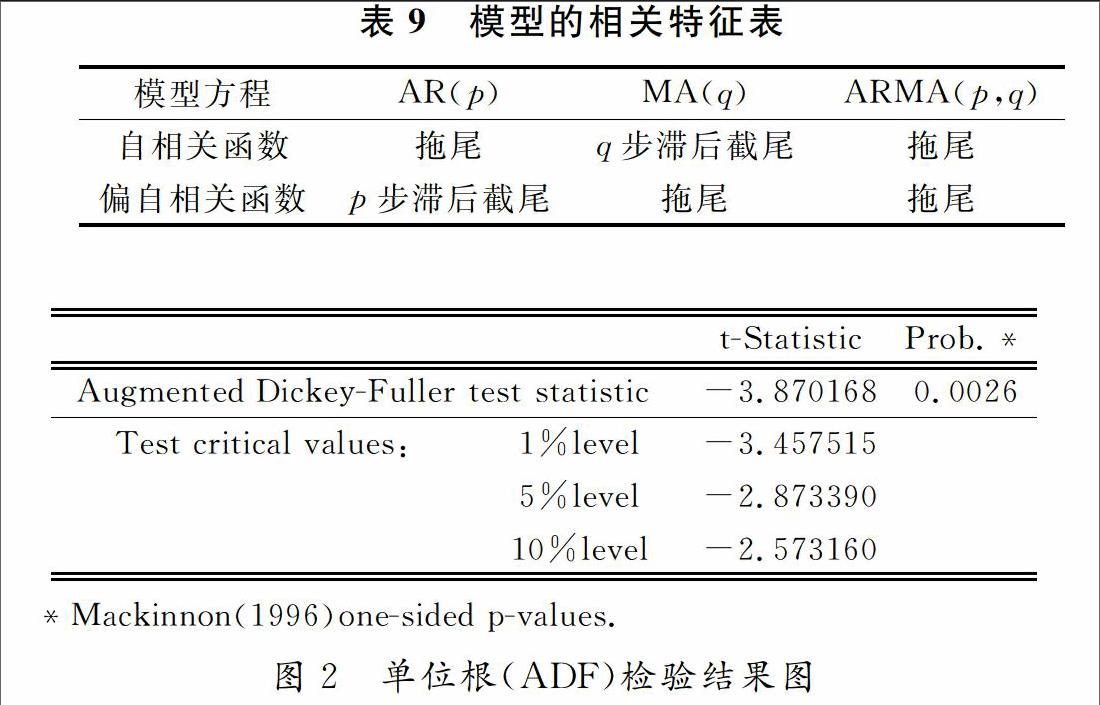
时间序列模型分为ARIMA和ARMA两种表现形式.其中前者是自回归移动平均结合模型的简写，可采用它对利用差分的方法对序列的平稳性作出分析.后者是建立在AR（p）和MA（q）这2种模型基础上的.但是在学术研究过程中，合理的使用ARMA模型比单纯使用AR或MA模型更加方便.

此模型的一般形式為：

3.2模型检验

经过上文模型建立部分的分析，最终完成出了9月21号和27号预测值，其值为50和48；而8月30号和31号的真实值分别为52和50，可以计算出其相对误差分别为4.8%和3.7%.由此可以看出，采用模型（ARMA）较好的预测分析了PM2.5浓度的波动变化情况以及短期的预测情况，显而易见表明通过建立时间序列模型对PM2.5波动变化进行预测、分析的合理性.然后，本文结合长沙市的实际情况以及季节因素给出了实际环境与PM2.5浓度波动变化情况进行定性分析.最终，通过前期的准别以及中期的建模部分，证明了本文建模思路的正确性，从一定程度上说明了较为成功的对于长沙市PM2.5的实际情况进行分析.有效的建立模型，为政府的相关决策可以提供可行性建议.

4空气质量控制管理建议

上文从统计分析的角度对长沙市PM2.5的相关问题进行分析，得知PM2.5与SO2、NO2、PM10、CO、O3间的相关关系.除此之外，对全市2015年度的PM2.5数值进行分析，发现其随季节展现出的不同波动性.结合本地区实际自然环境状况、季节特点等因素对PM2.5的成因进行分析，由此对我国政府的相关政策提供可行性建议如下：

①加强汽车油品提升，促进新能源使用

提升汽油、柴油油品，加大对燃气等新能源的替代使用.鼓励推动新能源之外，长沙地区工厂、公司及居民区应该加强对燃煤锅炉的清洁能源替代，同时大力监管市内其他燃煤锅炉的清洁能源替代，推进无燃煤街道创建，使长沙市创建为无燃煤市.

②加强扬尘监管，建设文明城市

加强对于城市建筑建设的环保处理，大力采用洒水装置车的使用.继续加大市容保洁能力建设，通过增加机械化保洁设备治理产生的扬尘，规范市场行为.改进道路保洁作业方式，强化渣土运输管理，扩大机扫率及冲洗率等方式提高市容道路保洁能力.

③加强大气污染监管

加强对大气环境污染源的执法力度，强化堆场、码头，合理规划与调整堆场.加大现场监察和监测频次，重点开展区域内工地负责人，强化规范化整治.继续加强对污染道路及周边的保洁作业，对重点单位实施“关改并举”的原则，明确湘江区域规划时序，指定主要大气污染物排污许可制度，整合各项管理资源，形成条块合力，严控排放总量，推广高压冲洗保洁工艺，对不符合区域发展定位，超标单位实施限期治理.

参考文献

[1]杨新兴， 冯丽华， 尉鹏. 大气颗粒物 PM2.5 及其危害[J]. 前沿科学， 2012， 6（21）： 22-30.

[2]陈伟. 基于小波分解和SVM的城市大气污染浓度预测[J]. 现代电子技术，2011，34（13）：146-148.

[3]孙斌. 基于灰色系统理论对西安市大气主要污染物的变化趋势分析及预测[J]. 上海环境科学，2015，34（3）：117-121.

[4]晓开提·依不拉音. 乌鲁木齐大气污染与循环系统疾病日住院人数的时间序列分析[J]. 卫生研究，2013，42（4）：682-685.

[5]王爱平， 张功营， 刘方. EM 算法研究与应用[J]. 计算机技术与发展， 2009， 19（9）： 108-110.

[6]欧阳钧， 王爱枝. 基于Matlab 的 BP 神经网络在大气污染物浓度预测中的应用[J]. 环境科学与管理， 2009， 34（11）： 176-180.

[7]刘文军，郑国义，田学. 西安市PM2.5相关因素多元回归分析模型[J]. 经济数学，2015，32（1）：85-88.

[8]吴健生，廖星，彭建，等.重庆PM2.5浓度空间分异模型及影响因子[J].环境科学，2015，6（3）：760-767.

2.4PM2.5与其他指标的灰色关联分析

灰色关联分析是根据系统变化发展趋势的相似或相异程度定量衡量因素间关联程度的一种方法.关联度描述系统发展过程中因素间的关联程度，它是指对2个系统之间的因素，随不同时间变化而产生的相对变化情况，其理论工具是灰色关联度.在体系发展中，倘若2个因素在发展过程中具有一致的变化趋势，则表示两者间的灰色关联度大；反之，则较低.与此同时，也可以用计算得出灰色关联度的大小情况判断因素之间的相关性程度.通过查阅文献，灰色关联分析的具体步骤如下：

①确定反映系统行为特征的分析序列

定性分析问题之前，确定因素间的关系.设因变量数据构成分析序列{x′i（k）}，各自变量数据构成比较序列，表示为：

2，PM10，CO和O3之间的相关性[4]，然后利用时间序列分析理论对长沙市PM2.5问题的数据进行分析，建立合理的时间序列模型并对长沙市PM2.5进行预报.