基于组合赋权与贝叶斯模型的建设风险评价

陈蓉

（陕西国防工业职业技术学院建筑与热能工程学院，陕西户县 710300）

基于组合赋权与贝叶斯模型的建设风险评价

陈蓉

（陕西国防工业职业技术学院建筑与热能工程学院，陕西户县 710300）

针对传统工程建设质量风险评价中存在的不确定性，提出一种基于灰色关联算法和贝叶斯模型的工程风险挖掘与评价算法。运用组合赋权的灰色关联法从工程项目中挖掘质量风险因素，并对这些因素进行顺序排序。在得到的风险权重指标中引入区间数，通过可能度矩阵对贝叶斯模型借助模型概率进行修正，实现对不同施工方案的整体质量评价。最后，以湖南常张高速作为背景，应用Matlab软件对评价算法进行可行性验证。

灰色关联法；贝叶斯模型；工程项目；风险评价；算法

随着现代计算机技术的不断发展，信息技术开始逐步应用到各个领域之中，为各领域的发展奠定了坚实的基础。而在工程建设中，对于质量风险的识别和判断，通常具有较大的主观性。风险评估是从施工源头查清风险因素，合理确定风险等级，但当前在对项目风险评估中，大部分都是依靠专家经验打分。即便存在对数据的客观分析，但很多都是以大量的数据作为基础，并很难将不同的数据指标进行量化处理。因此，如何利用现代信息技术，从有限的信息中提取和分析不确定性的风险，并客观地进行分析是本文研究的重点。对此，本文提出一种基于灰色关联和贝叶斯模型算法，就如何实现功能风险评估进行探讨。

一、研究思路

结合相关算法，本文对工程建设项目的风险评价中，首先采用主观和客观组合的方式对风险因素进行识别；其次，利用引入区间定义数，利用可能度矩阵求解排序向量，并利用贝叶斯模型的概率修正能力，对计算误差与实际误差进行修正，从而提高风险评价的质量。具体思路则（如下图所示）。

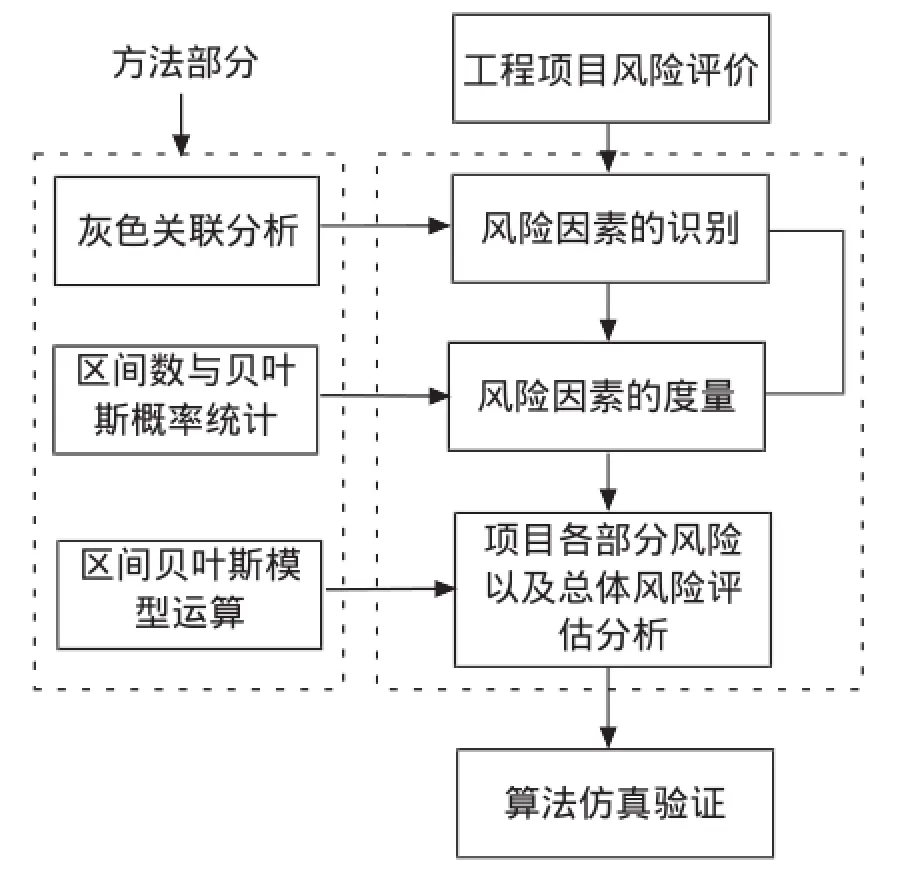
本文研究思路设计图

二、基于灰色关联算法的权重识别

（一）传统灰色关联算法

作为一种常用的多因素关联分析方法，通常对序列之间的几何相似度进行计算，从而作为主要的评价参照。因此，在该算法中，首先会在大量的数据中找到其可参考的序列，通常的方法是找一个极值序列X0j={X01，X02，……，X0m}作为参考，其余序列则作为比较序列Xij={Xi1，Xi2，……，Xij}。由此，可得到灰关联系数εij的计算公式为：

其中，灰色关联度为：

（二）灰色关联算法的改进

在公式（2）中，分辨系数ρ的主要作用是数据中出现的异常值，从而给关联度计算结果带来的误差。通常，在对灰色关联算法的应用中，将ρ的值设定为0.5，但设定该值通常没有考虑数值本身具备的特征，从而削弱了该系数的作用。因此，本文结合上述的研究，提出一种组合赋权的方法，即将专家的评定作为主观权重a，将客观风险定义为权重β。

而对于β值的计算，本文则采用变异系数法，其具体的计算为：

1.根据数据信息，构造一个指标矩阵Y=（Yi）jnm。其中，n、m分别为评价对象和指标的数量。

2.根据上述构建的指标矩阵，计算不同指标的均值及其标准差s（j），具体计算为：

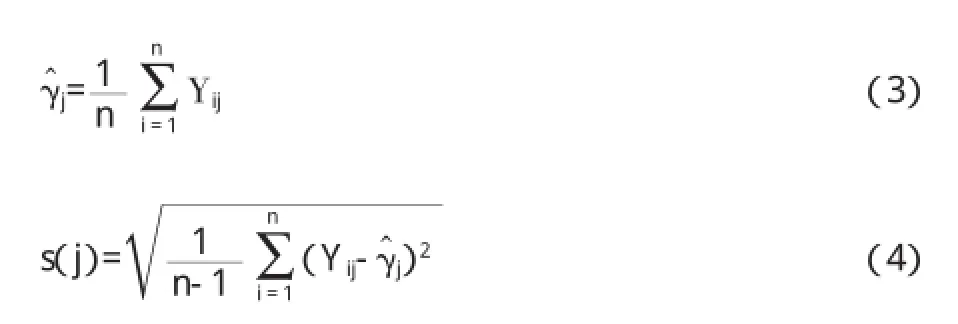
3.利用前面的计算结果，计算指标的标准差系数，将计算的结果采用归一化的方式处理，从而得到各个不同指标的客观权重：

因此，通过主观和客观的权重计算后，可得到组合赋权，计算公式为：

三、基于贝叶斯模型的风险评价模型

当前，在建设工程项目的信息化管理中，大部分还是基于建设经验来判定，但这种方式很难客观的评价风险。因此，本文引入贝叶斯模型，在对风险进行识别的基础上，还需要对风险指标的权重进行进一步的排序和修正，从而提高方案风险评价的质量。

（一）区间数定义

记A=[a-，a+]={x|a-≤a≤a+，x∈R}，其中A为一区间数，当a-=a+时，表示A退化为实数。其基本的运算法如下：记A=（aL、aU）和B=（bL、bU），且β≥0，则有如下：（1）A+B=（aL+bL，aU+bU）

（2）βA=（βaL，βaU），特别当β=0时，则βA=0。

通过上述的定义，将原本的项目风险问题描述为区间数，而通过贝叶斯模型计算得到的结果，其仍然为区间数。而对区间数大小的比较，必须要因素区间数比较方法。

（二）基于可能度比较的区间数排序方法

在对区间数中的向量进行排序中，首先要求解出一个可能度矩阵，并通过该矩阵中的行数据，才能对相应的向量进行排序，其具体运算为：

假设G=（gi，j）n*n表示n阶模糊判断矩阵，通过计算可得到可能度矩阵P=（pij）n*n的排序向量，记作v=（v1，v2，……，vm），由此根据计算可以得到所有排序向量的集合，记为∧。

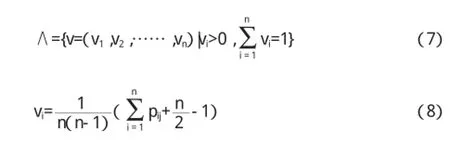
（三）基于区间排序的贝叶斯风险评估步骤设计

结合建设项目的实际需求，将该算法的步骤设计为：

1.首先确定某工程项目的建设方案集合，表示为{ai（}i=1，2，……，m），以及其自然状态集合{θj（}j=1，2，……，n）。

2.采用专家估计和对历史数据的分析，可得到自然态的先验概率π（θ）j。

3.根据对某类型工程项目历史数据的分析，并参考相应的专业数据库，得到对应的条件概率，由此将上述求解的先验概率和条件概率代入贝叶斯模型中：

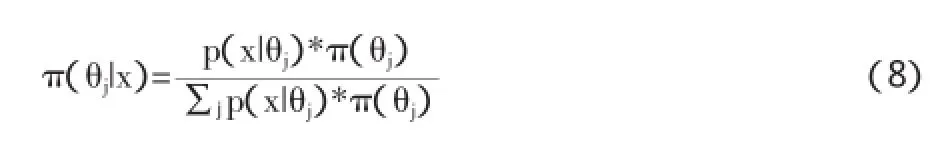
根据公式（8），即可求解出不同风险因素可能引发的后验概率值。

4.根据历史数据，得到每个项目方案的在自然状态下的风险影响值，同时以（fθj，a）j作为风险损失的函数，采用区间数的方式对不确定性风险进行表示。

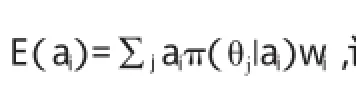
6.在得到不同方案的风险期望值后，运用可能度矩阵算法对数值进行比较，从而比较不同方案的可能度pij=p（E（a）i≥E（a）j）的大小，将比较结果构建成可能度矩阵P=（pi）jn*n。

7.根据上述的可能度矩阵，运用排序公式求解出矩阵的排序向量v=（v1，v2，……，vm），并根据分值的大小进行排序，从而求解出最优的选择方案。

四、算法验证

为进一步验证上述算法，通过对湖南建工常张高速建设项目的相关数据（数据量大，省略）的统计分析，得出各个因素引发事件的先验概率和条件概率。同时，在常张高速项目中，设计三个不同的施工方案。因此，应用Matlab软件建立设计模型，比较不同方案的建设风险。根据统计分析，可计算得到贝叶斯概率矩阵：

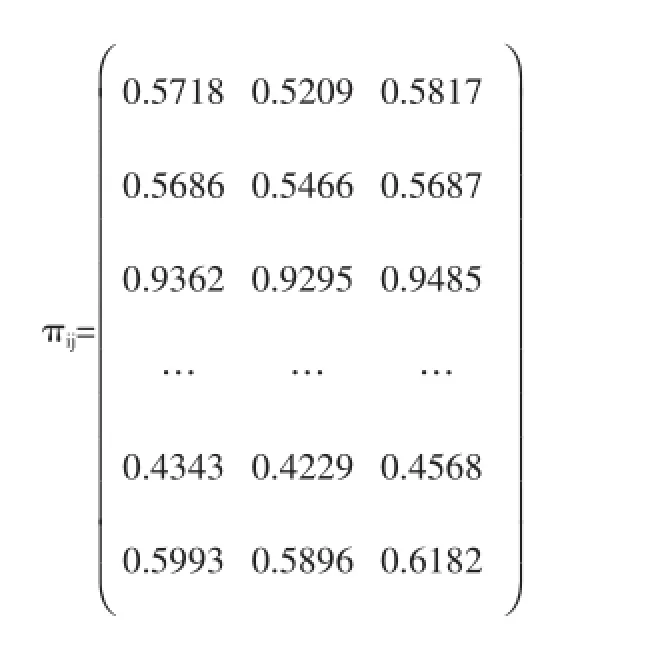
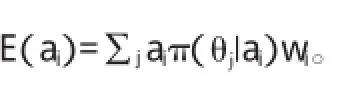
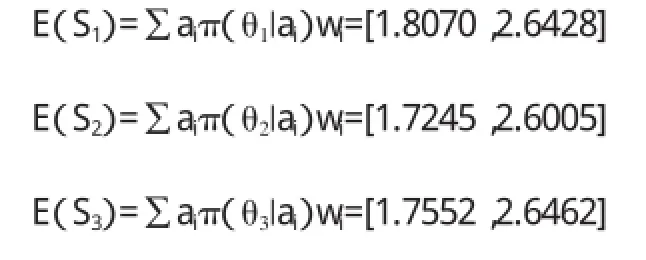
利用可能度法，对区间数进行排序，从而得到：

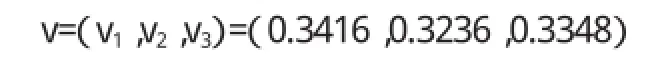
通过上述的分析可以看出，对于方案二的风险最小，整体风险为0.3236，因此可推荐方案二作为整体的建设施工方案。

但该评价结果只代表整体风险，并不代表方案为最佳方案。对此，运用组合赋权算法将整体建设风险划分为人员风险、施工风险、管理风险、环境风险等四个不同风险，并分别利用贝叶斯模型对不同方案的这些风险进行比较分析。如通过对管理因素的风险值、各个因素的权重值以及贝叶斯概率等，计算得到三个方案的不同施工风险影响值，并通过可能度法得到排序向量：

由上述计算得到，三套方案中，方案二和方案三在管理方面的因素存在的风险要高，而方案一的管理因素产生的质量风险要低，由此看出方案一更利于对团队的管理。

五、结论

本文针对工程建设中存在的风险不确定性问题，在传统风险评估的基础上，引入贝叶斯模型，从而对整体建设方案的风险质量进行评估分析，并通过对不同方案风险的分析，让建设项目的管理者能够找到不同方案的优势和不足，从而更好地弥补建设方案，提高信息化与建设施工的效果。

[1]王俊华，左万利，闫昭.基于朴素贝叶斯模型的单词语义相似度度量[J].计算机研究与发展，2015，(7)：149-150.

[2]李明亮.基于贝叶斯统计的水文模型不确定性研究[D].北京：清华大学，2012.

[3]王建，邓卫，赵金宝.基于改进型贝叶斯组合模型的短时交通流量预测[J].东南大学学报：自然科学版，2012，(1)：162-167.

[责任编辑 李晓群]

C931

A

1673-291X（2017）09-0178-04

2016-12-18

陈蓉（1982-），女，陕西眉县人，讲师，硕士研究生，从事工程造价与管理方面的教学与研究。