考虑泥页岩黏弹性的钻井液密度计算方法

屈展王萍吴学升崔莹张燕娜

1. 西安石油大学石油工程学院；2.西安石油大学机械工程学院；3.中国石油长庆油田公司油气工艺研究院

考虑泥页岩黏弹性的钻井液密度计算方法

屈展1王萍2吴学升3崔莹2张燕娜3

1. 西安石油大学石油工程学院；2.西安石油大学机械工程学院；3.中国石油长庆油田公司油气工艺研究院

泥页岩地层受到外来流体侵入后，岩石具有明显的流变效应，易造成井壁坍塌。为了研究泥页岩井壁受入井流体影响产生的黏弹性力学行为对井壁稳定性的影响，建立了黏弹蠕变本构模型来反映井壁流变失稳破坏的力学机理与演化规律。根据井壁围岩受力推导出平衡方程、几何方程，结合物理方程和边界条件，得到考虑泥页岩黏弹性特性的钻井液密度方程。结合现场钻井数据给出不同时间、不同收缩速率下泥页岩的钻井液密度图版。结果表明：泥页岩地层钻进时，井眼的收缩速率越小，则所需的钻井液密度越大；井越深，钻井时间越长，所需钻井液密度越大。

泥页岩；黏弹性；井壁稳定；钻井液密度；计算方法

井壁失稳问题是石油钻井过程中普遍存在的一个复杂问题。从力学角度来说，井壁岩石所受到的破坏应力大于原始强度是井壁失稳的主要原因。1940年H. M. Westergard［1］对直井周围弹-塑性井眼的应力分布情况进行了描述，发表了关于井壁稳定问题的正式文献。1964年Faithurst［2］给出了考虑倾斜地层、倾斜井眼、三向不均匀应力场下线弹性的应力状态解。Terzaghi［3］提出了有效应力原理，随后的研究人员将其运用到井壁稳定分析中，对孔隙压力的影响进行了修正。Carroll［4］给出了统一的表达式：有效应力=总压力– C×孔隙流体压力（常数C≤1）。Biot［5］在1955年提出了多孔弹性介质理论，并应用到井壁稳定的研究中。国内对井壁稳定的力学研究以石油大学的黄荣樽［6］、陈勉［7］、邓金根［8］、金衍［9］等教授为代表。多年来，根据多孔弹性介质力学理论、岩石力学、声学及地质力学理论，系统研究了孔壁围岩的受力状态，岩石强度的测定方法，地应力的测量技术，泥页岩水化应力及其分布、相应计算方法等。以上研究将井壁围岩考虑成弹性多孔介质来进行研究。然而随着对井壁失稳问题的深入研究，可以发现，对于泥页岩地层按照弹性或弹塑性理论来描述和处理岩石材料与时间相关的黏弹性属性方面，存在一定的缺陷。井壁岩石处于地下流体环境中，受到入井流体侵蚀的强化学作用，具有明显的黏弹性效应，引入流变力学的方法来进行研究，才会更为确切［10-11］。油气钻井过程中，入井流体通过对岩石结构和力学参数的影响［12］，使得泥页岩的软化临界荷载或长期强度降低；而且在钻井过程中，由于岩石的含水率变化及流固耦合的影响，使岩石的力学参数和结构进一步恶化，使岩石黏弹性变形大大增加。当泥页岩吸水膨胀产生黏弹性时，井壁岩石往往产生缩径破坏，常造成卡钻、井眼失稳、固井后挤毁套管等事故，给钻井带来重大经济损失［13］。

依据所钻地层的坍塌压力与破裂压力来确定钻井液密度，保持井壁处于力学稳定状态，是现场钻井中防止井壁发生坍塌或塑性变形常用的方法［9，13-17］。因此针对泥页岩的黏弹性力学行为，通过黏弹蠕变本构模型来研究泥页岩井壁蠕变失稳破坏的力学机理与演化规律，给出考虑黏弹性后泥页岩层钻进的钻井液密度图版，具有非常重要的现实意义。

1 泥页岩物理模型

Physical model of mud shale

对岩石的黏弹性特性研究一般是通过蠕变实验来实现的。蠕变是指在恒定载荷作用下，试件的变形随时间的增加而增加的现象。

按行业标准将试样加工成直径为25 mm、长为50 mm的圆柱体，将试样浸泡在蒸馏水中饱和24 h；然后对试样进行三轴蠕变实验，在固定围压条件下对试件施加轴向预载，缓慢加载至额定荷载后停止，保持压力不变，记录瞬时应变量，并连续观测其位移；经过一段时间后，当蠕应变的速率趋于稳定，每隔1～2 h记录1次；当连续2 h内变形增量低于了0.001 mm/h，可以开始施加下一级载荷，重复上述步骤直到试样被破坏。

典型的蠕变曲线如图1所示。试件受力产生在初始点（在t=0时刻）的变形为弹性变形，Ⅰ段是蠕变的第Ⅰ阶段，在这一阶段中，应变速率随时间的增加而减小，称为过渡蠕变阶段；Ⅱ段其应变速率不随时间而变化，是一常数，称为稳态蠕变阶段；Ⅲ段的蠕变曲线稍上翘，蠕变速率逐渐增加，岩样随即发生剪切破坏，称为加速蠕变阶段。

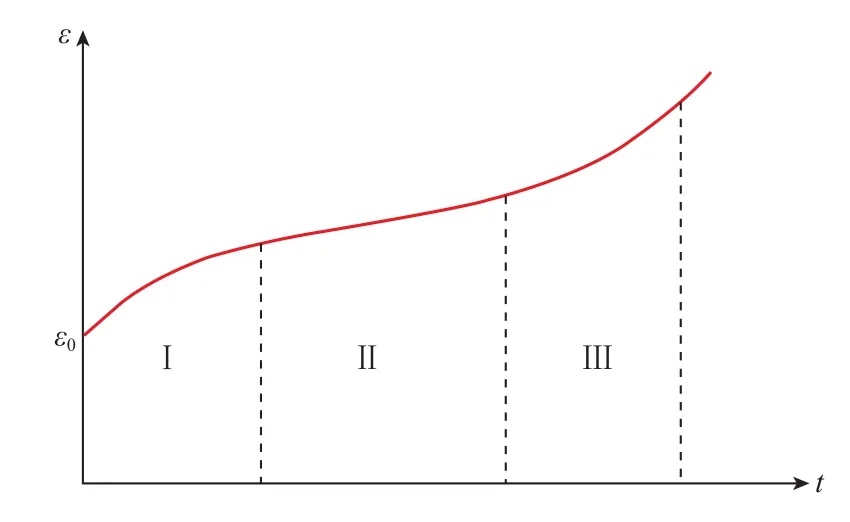
图1 典型的蠕变曲线Fig.1 Typical creep curve

对于钻井工程来说，第Ⅰ、Ⅱ阶段蠕变很重要，一般第Ⅰ阶段经历时间较短，第Ⅱ阶段持续的时间很长。第Ⅲ阶段持续时间也较短，岩石到了这一阶段后，将快速破裂，井壁围岩将很快发生失稳破坏。因此，在工程中主要考虑岩石变形呈黏弹性状态的稳态蠕变阶段对井壁稳定的影响。

实验结果进行分析，建立适合描述泥页岩蠕变特性的本构模型［18］

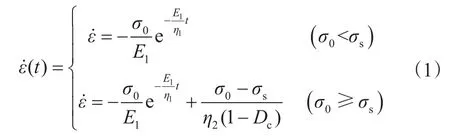
式中，E1为黏弹性模量，GPa；η1为黏弹性体的黏滞系数，GPa·h；η2为黏塑性黏滞系数，GPa·h；σ0为应力偏量，MPa；σs为屈服应力，MPa；Dc为岩石蠕变损伤量，无量纲；t为时间，h。

当岩体内的应力大于屈服应力σs时，将出现加速蠕变，其变形呈黏弹塑性状态，井壁围岩将很快发生失稳破坏。所以这里主要考虑应力小于屈服应力σs时，井壁围岩长时间处于稳定蠕变阶段，其变形呈黏弹性状态，据此可对上述模型进行简化。当井壁上应力差小于井壁泥页岩屈服应力时，井壁发生稳态蠕变， 黏弹性变形对钻井安全产生的影响。

2 井壁围岩受力模型

Force model of rocks around wellbore

岩石剪切破坏与否主要受岩石所受到的最大σ1、最小主应力σ3控制，两者的差值越大，井壁越易坍塌。井壁处岩石最大和最小主应力分别为周向应力和径向应力，这说明导致井壁稳定的关键是井壁岩石所受的周向应力σθ与径向应力σr的差值，即（σθ-σr）大小。则将式（1）变换得物理方程

主要考虑垂直井具有均匀水平地应力岩层的情况。井眼围岩的受力情况参照图2。

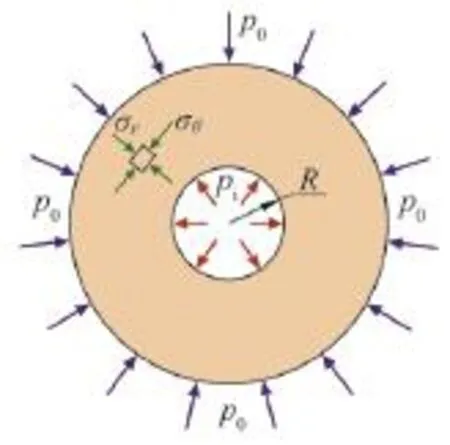
图2 井壁围岩受力模型Fig. 2 Force model of rocks around wellbore

由于岩层较厚，井筒较深，可以不考虑垂直方向产生的应变，简化成平面应变问题。设泥页岩地层地应力为均匀的，其值p0=（σH+σh）/2， σH、σh为最大、最小水平地应力，井内钻井液柱压力为pi，井眼半径为R；根据上述假设，可得井眼围岩受力模型的基本方程［9］。

对于轴对称问题，平衡方程为

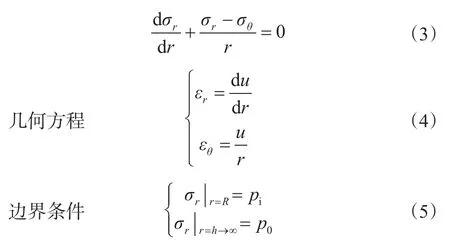
式中，σr为径向应力，MPa；σθ为周向应力，MPa ；u为位移，m。

将几何方程中径向和周向的应力分量对时间t求导，然后将两式合并得，又有，解得

式中，c为待定常数。

将式（3）和式（6）代入式（2）中，根据边界条件式（5）求解可以得到

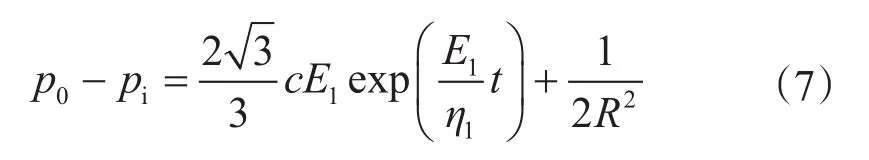
定义井眼的收缩速率n为

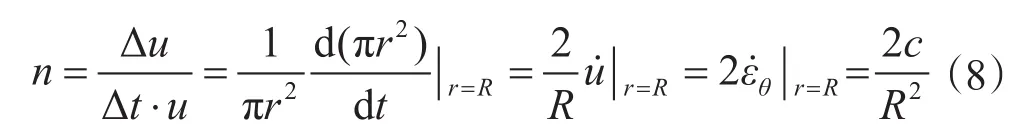
变换式（8）得：c=R2n/2。将c代入式（7）得

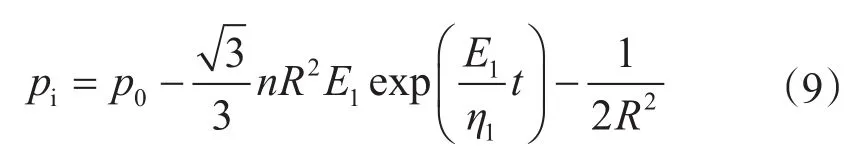
pi与p0均为井深H的函数，pi直接与钻井液密度有关。将式（9）给出稳定井眼所需的钻井液液柱压力，除以井深H，即得到所需的钻井液密度。

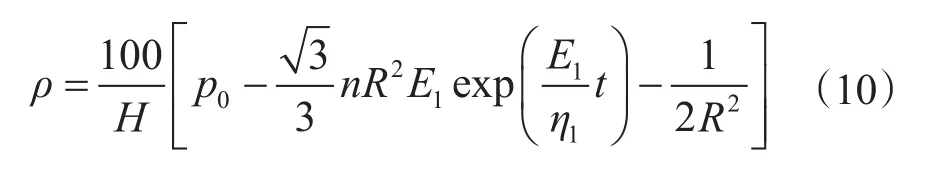
3 工程应用

Engineering application

某井现场数据：井深H为2 420 m；井眼半径R为139.7 mm，地应力取平均水平地应力p0=（σH+σh）/2=42.8 MPa，地层黏弹性模量E1取平均值40.65 GPa，黏弹性黏滞系数η1取平均值68.31 GPa·h，代入式（10），得到该地层不同井眼收缩速率下泥页岩层钻井所需的密度图版。

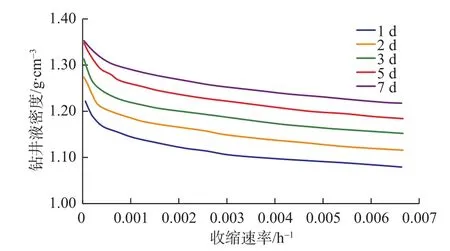
图3 不同时间、不同收缩速率下泥页岩的钻井液密度图版Fig. 3 Density chart of drilling fluid in mud shale with different shrinkage rates and times

从图3不同时间、不同收缩速率下泥页岩的钻井液密度图版可以看出，井眼的收缩速率越小，则所需的钻井液密度越大；随着钻井时间的延长，则所需的钻井液密度越大。

若控制井眼收缩速率n=0.001 h-1，得到该地层不同井深条件下泥页岩层钻井所需的密度图版，如图4所示。随着井深的增加，则所需的钻井液密度越大；同时随着钻井时间的延长，所需的钻井液密度越大。

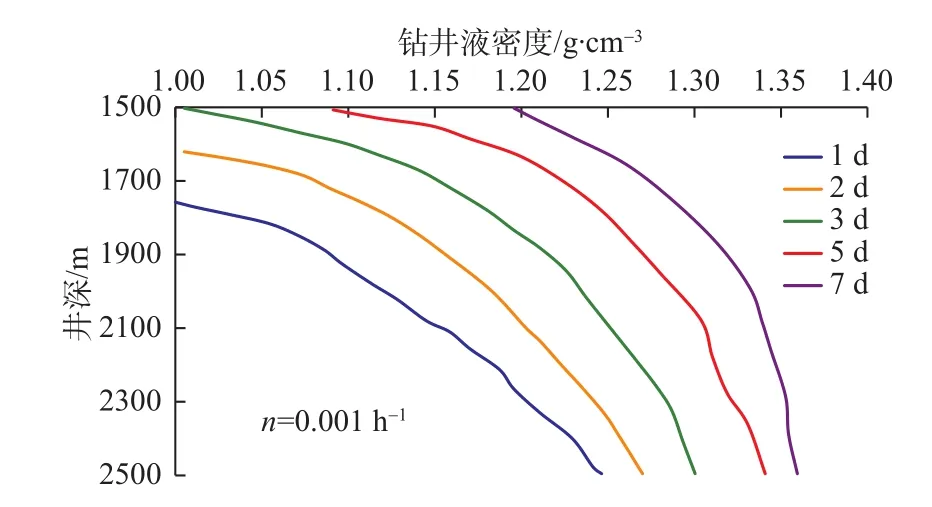
图4 考虑黏弹性特性后泥页岩层的钻井液密度图版Fig. 4 Density chart of drilling fluid in mud shale with consideration of viscoelastic characteristics

实际钻井中上部地层（井深小于1 600 m）的井径扩大率达到15%～40%，这是由于实用钻井液密度小于剪切坍塌压力当量密度所致。按设计计算结果，将钻井液密度1.12 g/cm3调整1.3 g/cm3后，井壁坍塌掉块现象明显改善。

在2 000 m以下虽然钻井液密度大于剪切坍塌压力当量密度，仍有20%～30%的井径扩大率，这是因为钻井液液柱压力仍小于泥页岩中的孔隙压力，从而产生了井壁拉伸崩落的结果。根据设计计算结果，随着井深的增加，钻井时间的增长，所需的钻井液密度越大。经过调整后，现场应用效果明显，保证了钻井的正常进行。计算结果经过现场使用验证，与实际情况符合很好，表明所用计算方法正确。

4 结论

Conclusions

（1）针对泥页岩的黏弹性力学行为，通过黏弹蠕变本构模型研究了井壁流变失稳破坏的力学机理与演化规律。

（2）根据井壁围岩受力推导出平衡方程、几何方程，结合物理方程和边界条件，得到考虑泥页岩黏弹性特性的钻井液密度方程。

（3）不同时间、不同收缩速率下泥页岩的钻井液密度图版可以看出井眼的收缩速率越小，则所需的钻井液密度越大；井深越大，钻井时间越长，所需的钻井液密度越大。

References:

［1］ WESTERGARD H M. Plastic state of stress around a deep well［J］. Boston Society of Civil Engineers, 1940, 27（1）: 1-5.

［2］ FAIRHURST C. Measurement of in SITU rock stress, with particular References to hydraulic fracturing ［J］. Rock Mechenggeol, 1964, 11（2）: 129-147.

［3］ TERZAQHI K. Theoretical soil mechanics［M］. New York: Wiley and Sons, 1943: 16-18.

［4］ CARROLL M M. Mechanics response of fluid-saturated porous materials［J］. In Heoretical and Annlied Mechanics, 1980, 12（5）: 17-23.

［5］ BIOT M A. Theory of elasticity and consolidation for a porous anisotropic solid［J］. Journal of Applied Physics, 1955, 26（2）: 182-185.

［6］ 黄荣樽. 泥页岩井壁稳定力学与化学的耦合研究［J］.钻井液与完井液，1995，12（3）： 18-24，28. HUANG Rongzun. Study on shale stability of wellbore by mechanics coupling with chemistry method［J］. Drilling Fluid and Completion Fluid, 1995, 12（3）: 18-24, 28.

［7］ 陈勉，金衍. 深井井壁稳定技术研究进展与发展趋势［J］. 石油钻探技术，2005，33（5）：28-34. CHEN Mian, JIN Yan. Advances and developmental trend of the wall stability technique［J］. Petroleum Drilling Techniques, 2005, 33（5）: 28-34.

［8］ 邓金根，程远方，陈勉，蔚宝华. 井壁稳定预测技术［M］.北京：石油工业出版社，2008：150-151. DENG Jin’gen, CHENG Yuanfang, CHEN Mian, WEI Baohua. Shaft stability prediction technology ［M］. Beijing: Petroleum Industry Press, 2008: 150-151.

［9］ 金衍，陈勉. 井壁稳定力学［M］. 北京：科学出版社，2012：56-58. JIN Yan, CHEN Mian. Shaft stability mechanics ［M］. Beijing: Science Press, 2012: 56-58.

［10］ 孙钧. 岩石流变力学及其工程应用研究的若干进展［J］. 岩石力学与工程学报，2007，26（6）：1081-1106. SUN Jun. Rock rheological mechanics and its advance in engineering applications［J］. Chinese Journal of Rock Mechanics and Engineering, 2007, 26（6）: 1081-1106.

［11］ 赵雄虎，韩斅，徐同台.微流变学研究钻井液静态黏弹性特征［J］. 钻井液与完井液，2015，32（1）：7-9. ZHAO Xionghu, HAN Xiao, XU Tongtai. Study on static viscoelastic characteristics of drilling fluid using micro-rheology［J］. Drilling Fluid & Completion Fluid, 2015, 32(1): 7-9.

［12］ 温航，陈勉，金衍，招军，叶西安，杨顺辉. 钻井液活度对硬脆性页岩破坏机理的实验研究［J］. 石油钻采工艺，2014，36（1）：57-60. WEN Hang, CHEN Mian, JIN Yan, ZHAO Jun, YE Xi’an, YANG Shunhui. Experimental research on brittle shale failure caused by drilling fluid activity［J］. Oil Drilling & Production Technology, 2014, 36（1）: 57-60.

［13］ 杨春和，曾义军，吴文，陈锋. 深层盐岩本构关系及其在石油钻井工程中的应用研究［J］. 岩石力学与工程学报，2003，22（10）：1678-1682. YANG Chunhe, ZENG Yijun, WU Wen, CHEN Feng. Constitutive relationship of deep salt rock and its application to petroleum drilling engineering［J］. Chinese Journal of Rock Mechanics and Engineering, 2003, 22（10）: 1678-1682.

［14］ 刘玉石，白家祉，周煜辉，黄荣樽 . 考虑井壁岩石损伤时保持井眼稳定的泥浆密度［J］. 石油学报，1995，16（3）： 123-128. LIU Yushi, BAI Jiazhi, ZHOU Yuhui, HUANG Rongzun. Mud density for wellbores tability when formation rock is damaged［J］. ACTA Petrolei Sinica, 1995, 16 （3） : 123-128.

［15］ 丰全会，程远方，张建国. 井壁稳定的弹塑性模型及其应用［J］. 石油钻探技术，2000，28（4）：9-11. FENG Quanhui, CHENG Yuanfang, ZHANG Jianguo. Elastic & plastic model for borehole stability and its apllication［J］. Petroleum Drilling Techniques, 2000, 28（4）: 9-11.

［16］ 闫传梁，邓金根，蔚宝华，谭强，邓福成，胡连波. 压力衰竭储层井壁稳定性变化规律研究［J］. 石油钻采工艺，2013，35（3）：5-8. YAN Chuanliang, DENG Jin'gen, WEI Baohua, TAN Qiang, DENG Fucheng, HU Lianbo. Research on wellbore stability of pressure depleted reservoirs［J］. Oil Drilling & Production Technology, 2013, 35（3）: 5-8.

［17］ 蔚宝华，闫传梁，邓金根，刘书杰，谭强，肖坤. 深水钻井井壁稳定性评估技术及其应用［J］. 石油钻采工艺，2011，33（6）：1-4. WEI Baohua, YAN Chuanliang, DENG Jin'gen, LIU Shujie, TAN Qian, XIAO Kun. Evaluation and application of wellbore stability in deep water［J］. Oil Drilling & Production Technology, 2011, 33（6）: 1-4.

［18］ 王萍，屈展，黄海. 地层水矿化度对脆硬性泥页岩蠕变规律影响的试验研究［J］. 石油钻探技术，2015，43（5）：63-68. WANG Ping, QU Zhan, HUANG Hai. Experimental study the creep law of the hard brittle shale shale Under different salinity formation water［J］. Petroleum Drilling Techniques, 2015, 43（5）: 63-68.

（修改稿收到日期 2016-12-02）

〔编辑 薛改珍〕

Calculation method of drilling fluid density based on viscoelastic characteristics of shale

QU Zhan1, WANG Ping2, WU Xuesheng3, CUI Ying2, ZHANG Yanna3

1. College of Petroleum Engineering, Xi’an Shiyou University, Xi’an 710065, Shaanxi, China; 2. Mechanical Engineering College, Xi’an Shiyou University, Xi’an 710065, Shaanxi, China; 3. Oil and Gas Technology Institute, CNPC Changqing Oilfield Company, Xi’an 710018, Shaanxi, China

Due to the intrusion of foreign fluid, mud shale presents obvious rheological effect, so borehole collapse tends to happen easily. In order to investigate how the borehole stability in mud shale is affected by viscoelastic mechanical behavior which is caused by fluids in the well, a viscoelastic creep constitutive model was developed to show the mechanical mechanisms and evolution laws of borehole rheological instability and deterioration. Then, balance equation and geometric equation were derived according the force on the surrounding rocks of borehole. Combined with the physical equation and boundary conditions, the drilling fluid density equation based on viscoelastic characteristics of shale was established. And finally, density charts of drilling fluids in mud shale with different shrinkage rates over the time were plotted based on actual drilling data. It is indicated that the lower the borehole shrinkage rate is, the higher the drilling fluid density shall be. As the well depth and drilling time increase, the density of drilling fluid shall be increased.

mud shale; viscoelasticity; borehole stability; density of drilling fluid; calculation method

屈展，王萍，吴学升，崔莹，张燕娜.考虑泥页岩黏弹性的钻井液密度计算方法［J］.石油钻采工艺，2017，39（1）：33-36，41.

TE21

A

1000 – 7393（ 2017 ） 01 – 0033 – 04

10.13639/j.odpt.2017.01.006

:QU Zhan, WANG Ping, WU Xuesheng, CUI Ying, ZHANG Yanna. Calculation method of drilling fluid density based on viscoelastic characteristics of shale［J］. Oil Drilling & Production Technology, 2017, 39(1): 33-36, 41.

国家自然科学基金资助项目“力学与化学耦合下泥页岩井壁蠕变损伤失稳研究”（编号：51174162）；国家自然科学基金资助项目“基于构型力学理论的井壁损伤失稳研究”（编号：51674200）。

屈展（1957-），1982年毕业于西北工业大学，1994年博士毕业于西南石油学院，主要从事井壁稳定与钻井工程方面的研究工作，二级教授，博士生导师。通讯地址：（710065）西安市电子二路18号西安石油大学。E-mail：zhqu@xsyu.edu.cn