一种大尺度让压锚杆特性分析及其应用研究

杨喻声

(1. 同济大学地下建筑与工程系， 上海 200092； 2. 同济大学岩土及地下工程教育部重点实验室， 上海 200092)



一种大尺度让压锚杆特性分析及其应用研究

杨喻声1, 2

(1. 同济大学地下建筑与工程系， 上海 200092； 2. 同济大学岩土及地下工程教育部重点实验室， 上海 200092)

随着众多深、大、长隧道的建设，软岩挤压性大变形问题日益突出。让压锚杆是一种治理大变形问题的有效手段。介绍大尺度让压锚杆的结构及支护过程，并采用ANSYS软件验证大尺度让压锚杆弹性变形、滑动让压、杆体受拉3阶段的工作特性。采用基于Hoek隧洞挤压预测经验公式的概率分析方法和ABAQUS软件分别对让压锚杆的让压力和让压量研究，结果表明： 1)锚杆让压力存在下限值，岩体抗压强度越高，下限值越低； 2)让压量增大到一定程度后，再增加相同的让压量，二次衬砌压力降幅减小。利用大尺度让压锚杆的受拉阶段，实现“边支边让，先柔后刚”，可有效控制围岩大变形，提高隧洞的长期稳定性。

大尺度让压锚杆； 软岩大变形； Hoek经验公式； 让压力； 让压量

0 引言

随着国民经济的发展，隧道工程建设不断向更深更复杂的地层发展，原岩应力不断增加。高地应力会使软岩地下硐室、隧道发生挤压性大变形，是一种危害程度大、整治费用高的地质灾害[1]。国内外学者对此进行了大量的研究，提出了一些解决方案，诸如超前管棚支护[2]，可伸缩钢拱架[3-4]，主动松动卸压[5]，超长预应力锚杆结合扩挖、复挖[6]等方法。允许围岩发生一定程度的变形，在变形过程中施加一定的支护压力，即“边支边让”[1]已经成为治理软岩大变形问题的共识。

可适应较大变形的高强让压锚杆是一种能够有效治理软岩挤压性大变形问题的手段。何亚男[7]阐述了让压锚杆设计的基本原理，主要分2种： 1)采用塑性好的钢材制作杆体，利用杆体较大的延伸率实现让压，如图1(a)所示； 2)设置某种机械结构，利用机械结构的摩擦滑移特性实现让压，如图1(b)所示。近年来，国内外相继研发了多种新型让压锚杆，如改进型Cone锚杆[8]、新型耗能锚杆[9]、拉压耦合大变形锚杆[10]、让压管锚杆[11]、Garford锚杆[12]、Yield-Lok锚杆[13]、D锚杆[14]、NPR锚杆[15]等，其原理都是利用杆体塑性或机械结构的滑移特性。利用杆体钢材塑性的让压锚杆让压量受材料性能限制，理想状态下伸长率最大不超过20%，让压量有限。利用机械结构滑移原理设计的让压锚杆在工程实践中逐渐得到推广应用[15-16]，但让压锚杆让压力的大小和让压量的控制等关键问题尚未解决。

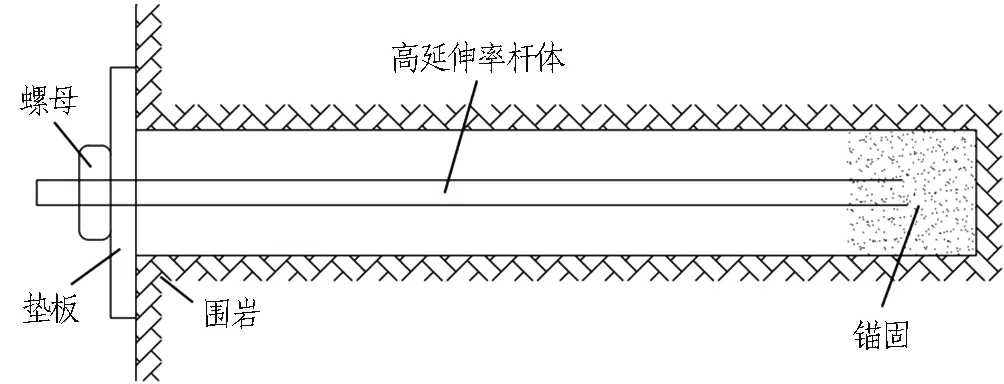
(a) 利用杆体塑性

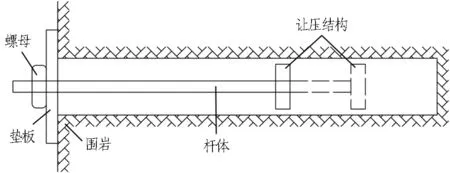
(b) 利用机械结构滑移

针对软岩挤压性大变形问题，孙钧先生近年与图强工程材料公司合作，研发了采用机械结构设计的大尺度让压锚杆[1,17]。郭永建等[18]对大尺度让压锚杆进行了室内和现场试验，验证了让压锚杆的让压特性。但对此种大尺度让压锚杆的定量分析以及机制研究较少。本文以大尺度让压锚杆为基础，采用ANSYS软件分析让压锚杆的受力特性及机制，基于Hoek经验挤压预测公式，采用概率分析法讨论让压力对隧洞变形的影响，并结合实际工程参数，利用ABAQUS软件分析让压量对二次衬砌压力的影响。

1 让压锚杆的结构及支护过程

1.1 让压锚杆的结构

同普通锚杆类似，大尺度让压锚杆由钻头、杆体和垫板等组成，在锚杆的端部设置具有让压功能的机构[19]。考虑到发生挤压性大变形的硐室或隧道地层条件较差，锚杆受力复杂，所以大尺度让压锚杆采用外让压方式，让压机构设置在垫板外侧，以保证让压效果。让压机构如图2所示，主要由挤压套管、空心杆体、垫板和螺母组成。挤压套管通过挤压机挤压成型，向内挤压空心杆体，使杆体外径缩小，增大其与挤压套管之间的压力，进而增大两者之间的摩擦力。让压时，垫板受到围岩荷载作用，推动挤压套管沿杆体向洞内运动，空心杆体受到挤压，收缩滑动。挤压套管与空心杆体之间的滑动摩擦力即为让压力，一般低于杆体屈服荷载，保证让压过程杆体材料处于弹性变形阶段。由于让压段杆体径向收缩量较小，对杆体损伤很小，杆体受拉性能基本不受影响，让压结束后可继续承载。

图2 大尺度让压锚杆

1.2 让压锚杆支护过程

围岩受隧道或硐室开挖扰动，产生变形。围岩变形初期，荷载大； 随着变形的发展，围岩荷载逐渐减小，直至最后稳定。让压锚杆在围岩变形稳定的过程中提供支护，边支边让，控制围岩变形，保证隧道或硐室的稳定。根据图强工程材料公司提供的让压锚杆典型特征变形曲线(如图3所示)，大尺度让压锚杆的支护过程大致分为4个阶段： 1)OA阶段。锚杆受力较小，低于挤压套管和空心杆体之间的最大静摩擦力，杆体与套管之间保持相对静止，杆体受拉，发生弹性变形，如图4(a)所示； 2)AB阶段。锚杆受力超过挤压套管与空心杆体之间的最大静摩擦力，套管沿杆体发生滑移，提供恒定的让压支护力，等于套管与杆体之间的滑动摩擦力，让压量可以根据工程需要设定，如图4(b)所示； 3)BC阶段。在B点，挤压套管与杆体端部的螺母接触，杆体被锁定，挤压套管与杆体再次保持相对静止，杆体受力增加。由于杆体钢材塑性好，断后伸长率可达16%及以上，杆体受力超过屈服荷载后，进入屈服强化阶段，继续支护，如图4(c)所示。在C点，达到锚杆极限让压量。此阶段让压锚杆杆体受拉提供支护力，远大于AB阶段的让压力，在工程设计时一般不利用； 4)CD阶段。杆体钢材进入颈缩阶段，发生断裂，让压锚杆失效。

2 让压锚杆有限元分析

相比于室内或现场试验，有限元模拟高效易行，可为后续现场试验参数选取提供参考，且便捷的参数优化功能也可对结构改进提供指导。所以，有限元分析对大尺度让压锚杆特性的验证以及进一步优化具有不可替代的作用。下文采用ANSYS软件对大尺度让压锚杆的工作特性进行分析。

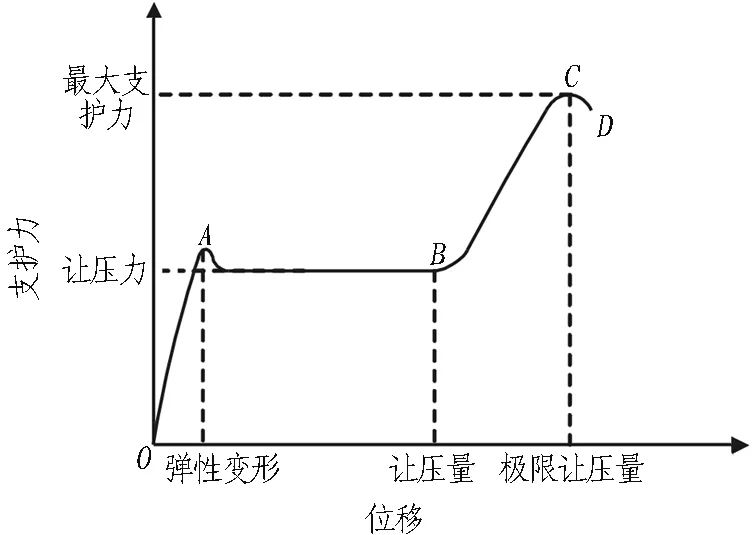
图3 大尺度让压锚杆变形曲线

Fig. 3 Deformation curve of yielding anchor bolt with large allowable deformation

(a) OA阶段

(b) AB阶段

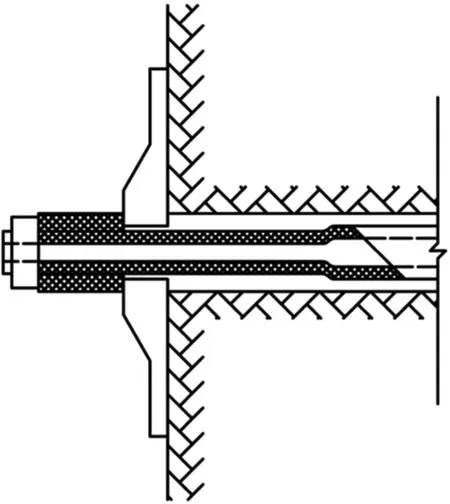
(c) BC阶段

Fig. 4 Support deformation of yielding anchor bolt with large allowable deformation

2.1 有限元模型

选用三维20节点六面体单元SOLID186模拟让压锚杆，对应的8节点接触单元TARGET170和CONTACT174建立挤压套管内表面与空心杆体外表面、螺母与挤压套管之间的接触关系。接触面初始间隙设为0.1 mm，参照钢结构设计规范，摩擦因数取0.4。预设锚杆让压量100 mm。利用对称性，取1/4模型分析，网格划分后的有限元模型如图5所示，模型参数如表1所示。杆体采用塑性好，延伸率大的软钢，材料本构选用双线性随动强化模型，以2条直线段描述钢材的应力应变关系，切线模量取790 MPa，材料参数如表2所示。有限元模型侧面施加对称位移约束，挤压套管施加轴向位移约束。采用位移加载方式，空心杆体前端施加120 mm位移荷载。

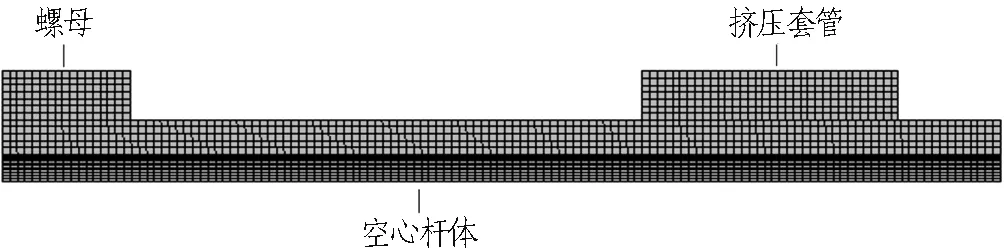
图5 有限元模型

Fig. 5 FEM model of yielding anchor bolt with large allow-able deformation

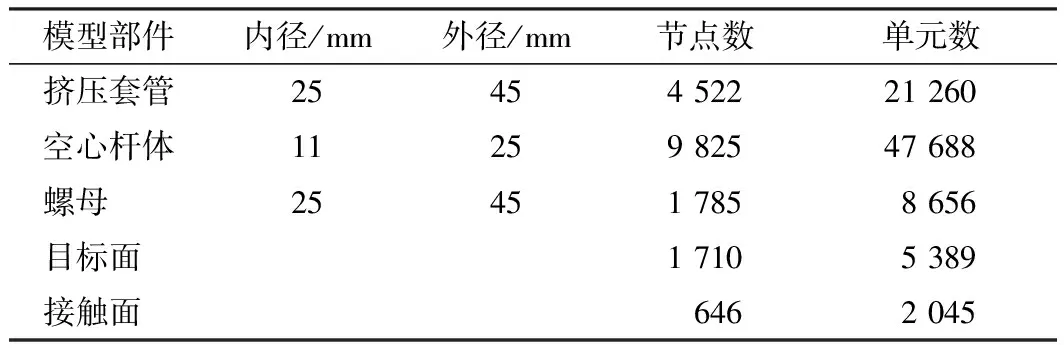
表1 模型参数

注： 接触面和目标面只计入挤压套管与空心杆体之间接触对。

表2 材料参数

分析过程共2个荷载步： 1)建立挤压套管与空心杆体之间接触压力。设置ANSYS接触模型的初始间隙参数，求解两者之间的接触压力； 2)支护过程模拟。空心杆体位移加载，分析让压锚杆的工作过程。

2.2 有限元结果分析

2.2.1 支护力-位移关系

让压锚杆支护力-位移曲线如图6所示。由图可知让压锚杆3阶段工作特性明显： 1)弹性变形阶段。支护力与位移呈线性关系； 2)滑动让压阶段。荷载超过最大静摩擦力后，挤压套管与空心杆体发生相对滑移，支护力由最大静摩擦力变为滑动摩擦力，略有降低，此后，支护力保持恒定； 3)受拉阶段。当空心杆体端部螺母与挤压套管接触后，杆体受力增加，支护力提高。滑动让压力一般低于杆体屈服荷载，在初期短暂的弹性变形后，进入屈服强化阶段，直至最终断裂破坏。

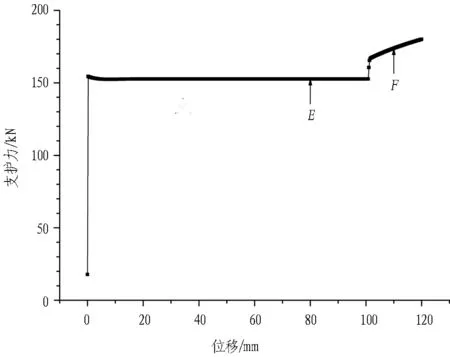
图6 让压锚杆支护力-位移曲线

Fig. 6 Support pressures vs. deformation of yielding anchor bolt with large allowable deformation

2.2.2 工作阶段性态

位移加载至80 mm和110 mm时，让压锚杆分别处于滑动让压阶段和杆体受拉阶段(见图6中E点和F点)，让压锚杆轴向弹性应变和塑性应变对比分别如图7和图8所示。由图可知： 位移等于80 mm时，让压锚杆处于让压阶段，杆体以弹性应变为主，塑性应变很小； 位移等于110 mm时，让压锚杆处于杆体受拉阶段，杆体弹性应变基本保持不变，但塑性应变急剧增加。杆体在让压阶段仅传递让压力，处于弹性阶段。杆体受拉阶段类似于普通锚杆发生屈服强化，直至最终断裂破坏。2阶段杆体工作性态不同，塑性发展水平有显著差异。

3 让压力大小

3.1 Hoek挤压预测经验公式

E. Hoek等[20]基于静水压力场中圆形隧洞解析解，利用Monte Carlo方法，建立了岩体强度应力比(岩体抗压强度和最大地应力比值)与隧洞变形之间的关系(见式(1))，并在此基础上，提出了隧洞挤压程度分类方法，得到了广泛认可。

ε=(0.2-0.25pi/p0)(σcm/p0)2.4pi/p0-2。

(1)

式中： ε为洞室收敛比，表示洞室内壁变形量与洞室直径的比值； pi为支护压力，当pi=0时，即为无支护时的经验预测公式； p0为竖向地应力和水平地应力的较大值； σcm为岩体抗压强度，由Hoek-Brown准则中相关参数计算。

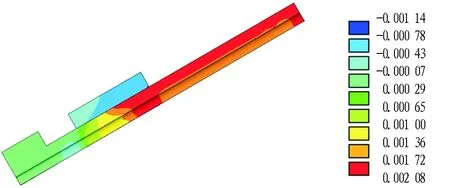
(a) 位移=80 mm(E点)

(b) 位移=110 mm(F点)

Fig. 7Elasticstrainsofyieldinganchorboltwithlargeallowabledeformation

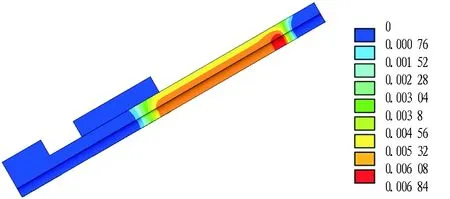
(a) 位移=80 mm(E点)

(b) 位移=110 mm(F点)

Fig. 8 Plastic strain of yielding anchor bolt with large allowable deformation

K.K. Panthi等[21]利用Hoek预测方法(式(1))分析Kaligandaki引水隧洞的收敛情况，与监测结果较为接近，验证了此方法的准确性。张传庆等[22]定义岩石峰值应变与岩石峰值应变参考值(0.73%)为潜在挤压比，表征不同岩石的变形能力，修正了Hoek预测方法，用于预测锦屏二期引水隧洞的挤压变形，证明Hoek经验预测方法是有效的。下文基于此方法，采用@Risk概率分析软件探究不同支护力大小对隧洞收敛比的影响。

3.2 概率分析模型

@Risk分析软件采用Monte Carlo方法模拟，在服从指定分布的输入量一定区间内随机取点，进行上千次的计算分析，来生成可能的结果分布。Hoek(某隧道)和K.K. Panthi(Kaligandaki引水隧洞)都采用此方法进行了隧洞收敛预测分析。本文首先采用相同的参数和输入分布形式建立概率分析模型，模拟结果与原文对比验证后，设置不同的支护力，以探究不同支护力大小对隧洞收敛的影响。

文献[20]假设地应力为正态分布，支护压力取定值1 MPa，且岩体抗压强度由Hoek-Brown准则中的参数单轴抗压强度σci、经验常数mi和地质强度指标GSI计算求得，其概率分析模型(以下简称Hoek模型)输入参数统计值及分布形式如表3所示。文献[21]认为地应力越大，发生挤压的可能性越高，故假设地应力的倒数1/p0为指数分布，同时假设支护压力为正态分布，其概率分析模型(以下简称Panthi模型)输入参数统计值及分布形式如表4所示。

表3 Hoek模型输入变量的统计值及分布形式

Table 3 Statistical values and distribution modes of input variable of Hoek model

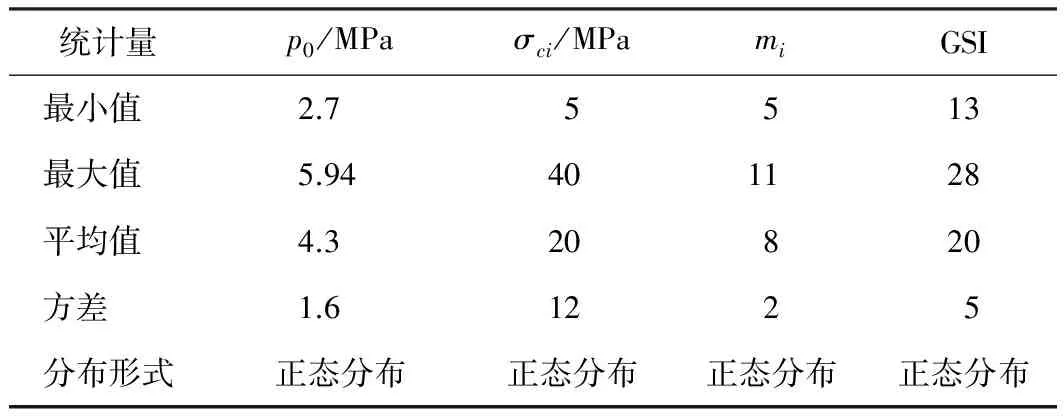
统计量p0/MPaσci/MPamiGSI最小值2．75513最大值5．94401128平均值4．320820方差1．61225分布形式正态分布正态分布正态分布正态分布

表4 Panthi模型输入变量的统计值及分布形式

Table 4 Statistical values and distribution modes of input variable of Panthi model

统计量p-10/MPa-1σcm/MPapi/MPa最小值0．062．470．46最大值0．0875．891．27平均值0．0734．050．71方差1．210．3分布形式指数分布正态分布正态分布

假设支护压力服从正态分布[21]。根据数理统计理论，服从正态分布的参数取值在平均值3倍标准差范围内的概率为99.7%，为讨论不同支护力对隧洞收敛的影响，支护力取0～1.5 MPa，不同支护力的输入统计值如表5所示。

3.3 让压力结果与分析

对不同支护力进行10 000次模拟迭代，Hoek模型和Panthi模型的累计概率分布如图9所示。由图可知： 支护力越大，相同的可靠度下，隧洞收敛比越小，即围岩变形更小，隧洞稳定性更好。

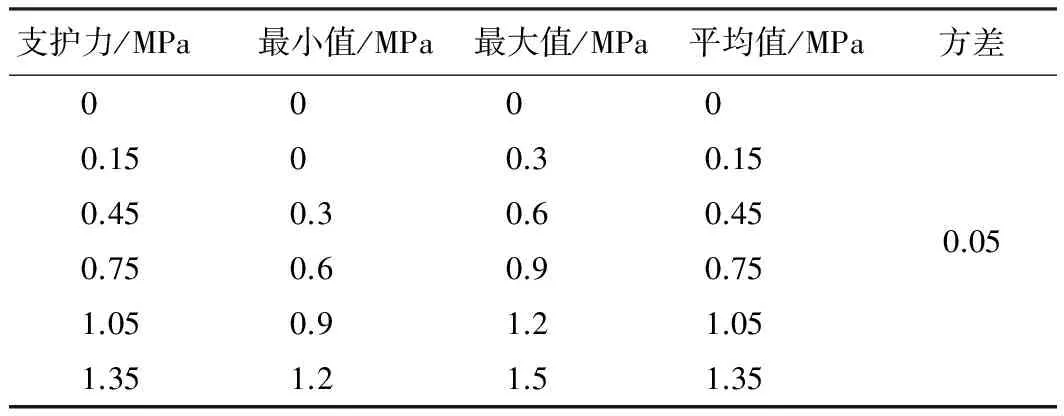
表5 不同支护力的输入统计值

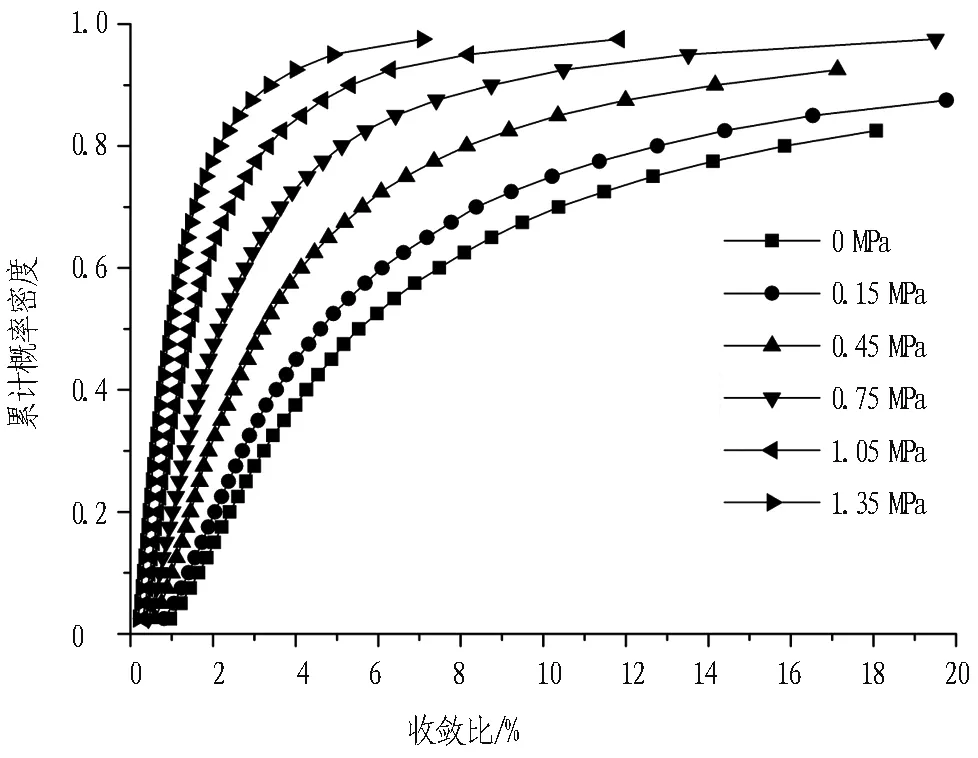
(a) Hoek模型

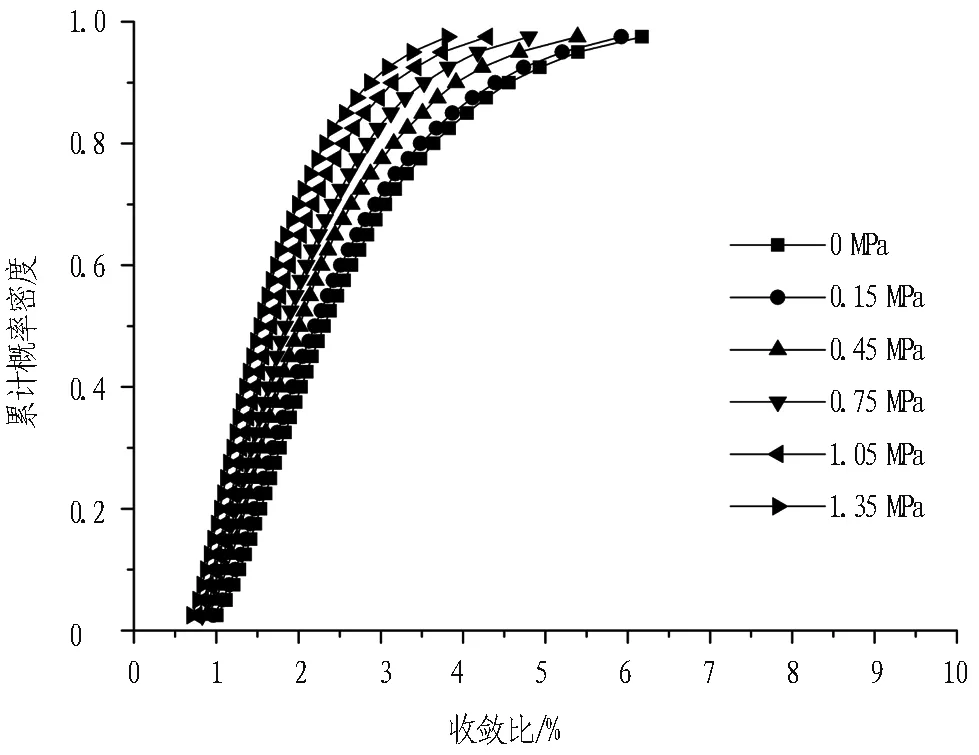
(b) Panthi模型

不同可靠度下，收敛比与支护力的关系如图10所示。由图可知： 随着支护力的增加，不同可靠度下隧洞收敛比差异减小。相同可靠度下，隧洞收敛比降幅随支护力增大而逐渐减小，具有明显的转折点。Hoek模型的结果比Panthi模型趋势更明显，可能与地应力分布形式假设不同有关。

(a) Hoek模型

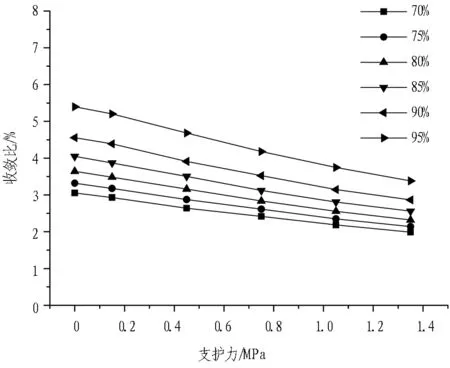
(b) Panthi模型

隧洞收敛比降幅随支护力增大而逐渐减小，具有明显的转折点，说明让压力存在下限值。基于Hoek经验预测公式，在不同岩体抗压强度与地应力比值下，支护力与地应力比值和收敛比的关系如图11所示。由图可知： 当支护力超过地应力的40%时，隧洞收敛比低于5%，可以有效控制围岩变形。岩体抗压强度与地应力比值增大时，收敛比曲线转折点左移，支护力的下限随之降低，即岩体抗压强度越高，支护力下限越低。

让压力的下限可以从收敛约束法的基本原理解释。如图12所示，无支护时，围岩发生一定变形后破坏； 当支护力较小时，让压锚杆支护曲线不与围岩收敛约束曲线相交，表明让压锚杆并没有形成有效的支

护，仅延缓了围岩的破坏。让压锚杆让压力大于围岩收敛约束曲线最低点所需的支护力时，即让压力的下限时，才能有效稳定围岩，控制变形。在工程应用时，应保证让压锚杆的让压支护力大于让压下限值。

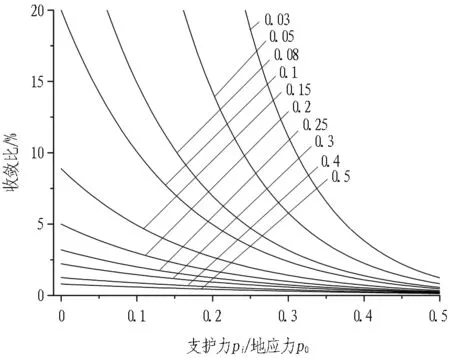
图11 支护力/地应力与收敛比的关系

Fig. 11 Relationships between convergence ratio and ratio of support pressure to ground stress

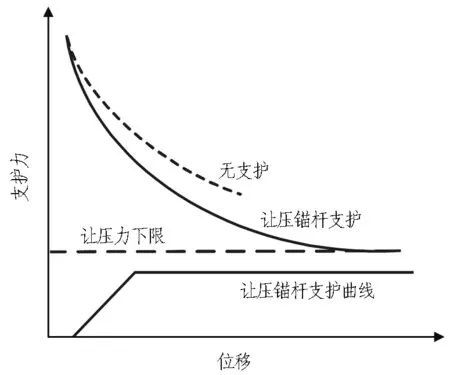
图12 让压锚杆支护力下限

4 让压量

4.1 有限元分析模型

国内旅游学术界对于游客感知价值尚未形成统一的标准，其中学者李文兵，张红梅在顾客感知价值的基础上提出游客感知价值是“游客在感知利得和利失的基础上对旅游产品或旅游服务在一定的旅游情境中满足其旅游需要程度的感知和评价”【4】。本文正是基于以上两位学者对于游客感知价值的定义，研究和评价民宿游客在感知利得和利失的基础上对于民宿旅游产品或服务是否满足其旅游需求的总体感知和评价。

4.1.1 岩体及支护参数

选用ABAQUS软件中的Drucker-Prager本构模型，采用乌鞘岭隧道围岩参数，如表6所示[23]。计算范围取60 m×60 m，中间开挖半径为5.38 m的隧道，左边界水平方向施加位移约束，下边界竖直方向施加位移约束，围岩侧压力系数为1.0，上边界、右边界作用岩体压力均约9.71 MPa。利用对称性，取1/4模型分析。

表6 乌鞘岭隧道岩体参数

初期衬砌在隧道开挖后立即施作，采用喷射工法，厚度和质量离散性均较大，加之隧道地应力高，围岩荷载较大，一般分析中采用弹性本构模型与实际情况不符。本文考虑初期衬砌的屈服，采用理想弹塑性模型，参照混凝土规范，屈服强度取10 MPa。二次衬砌为模筑混凝土，厚度和配筋率较大，质量可靠，采用弹性模型。衬砌计算参数如表7所示。

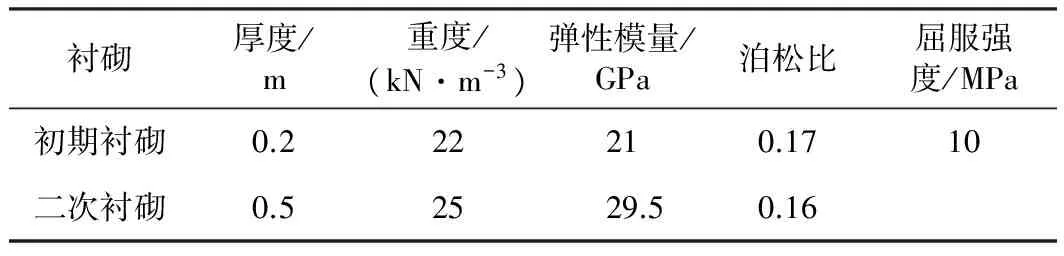
表7 衬砌计算参数

4.1.2 让压锚杆模拟

锚杆的有限元模拟方法主要有2种： 全长锚固型锚杆通常采用杆单元； 两端锚固式锚杆则采用1对相向集中力模拟。让压锚杆与普通锚杆不同，支护过程包括弹性变形、滑动让压和杆体受拉3阶段，要对让压锚杆精确建模，尺寸上的巨大差异加大了单元间耦合的难度，也提高了计算收敛的难度。如上文所述，实际工程设计中一般不利用杆体受拉阶段。考虑到开挖初期围岩压力极大，让压锚杆弹性变形阶段很短； 同时，让压锚杆让压过程中，杆体与孔壁之间尚未注浆，类似于两端锚固式锚杆。所以，为简化计算，本文采用1对相向集中力模拟让压锚杆，集中力大小取让压锚杆恒阻让压力。通过在二次衬砌与初期衬砌之间预留不同的间隙模拟不同大小的让压量。考虑垫板的作用，洞壁侧将集中力换算为等效均布荷载施加在围岩上[24]。让压锚杆有效工作的前提是锚固稳定，其锚固深度应较普通锚杆有相应提高，本文取5 m。让压锚杆布设方式采用工程中常见的1.8 m×1.8 m梅花形，等效平面布设如图13所示。恒阻让压力取150 kN，考虑对称作用，计算时拱顶和右帮恒阻让压力取1/2。采用提高岩体参数的方法模拟注浆与系统锚杆加固效果，将洞周3 m范围内施锚区岩体弹性模量和黏聚力分别提高30%[25]，即E=9.3 GPa，c=291.2 kPa，而内摩擦角和泊松比不变。

4.1.3 计算分析步

实际工程中，初期衬砌一般在隧道开挖后立即施作，考虑到开挖、施工等因素，初期衬砌发挥作用时围岩应力已有所释放。本研究采用在初期衬砌单元激活前降低开挖区域岩体弹性模量的方法，来模拟应力释放效应。关于应力释放率的取值，许多学者进行了相关研究，本研究取30%[25]。初期衬砌与围岩密贴，采用绑定约束模拟两者之间的接触。

图13 让压锚杆布设示意图

4.2 让压量结果与分析

二次衬砌压力与让压量的关系如图14所示。让压量增加，二次衬砌受到的压力逐渐减小。拟合关系表明二次衬砌压力与让压量呈对数下降关系，让压量增加到一定水平后，再增加相同的让压量，二次衬砌受到的压力降幅减小。

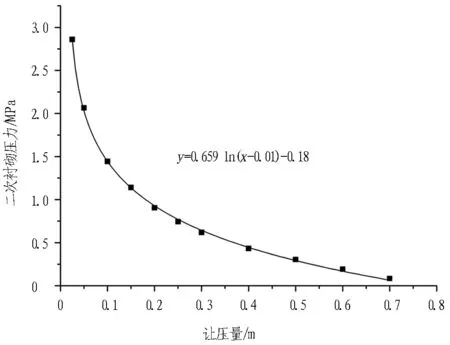
图14 二次衬砌压力与让压量的关系

Fig. 14 Relationships between pressures acting on secondary lining and yielding deformation

针对软岩大变形问题，工程实践中通常较早施作二次衬砌，限制围岩位移。而分析结果表明，隧道开挖初期，围岩荷载大，预留一定的让压量，再施作二次衬砌，利用让压锚杆“边支边让”的特点，能够有效控制围岩变形，减小开挖影响，改善围岩受力状态，保持围岩整体性，减小二次衬砌受到的压力。但让压量应适当，过大的让压量对降低二次衬砌压力效果不明显，同时易导致岩体裂隙发展，降低岩体整体性，不利于隧洞的长期稳定。

5 让压支护理念

让压锚杆的支护思想是“边支边让”。围岩变形初期，让压锚杆支护压力相对于围岩荷载较小，支护效果不明显，让压锚杆支护“以让为主”； 围岩变形发展到一定程度后，围岩荷载降低，而让压锚杆支护力稳定，逐渐控制围岩变形，进入“以支为主”的工作阶段，稳定围岩。让压锚杆的支护原理是在围岩变形的过程中挤压围岩，形成承压拱，利用围岩的自承作用； 同时，在让压过程中将等于锚杆支护力的围岩荷载传递到岩体深部，发挥让压锚杆的悬吊作用，调动深部岩体的支承力，如图15所示。

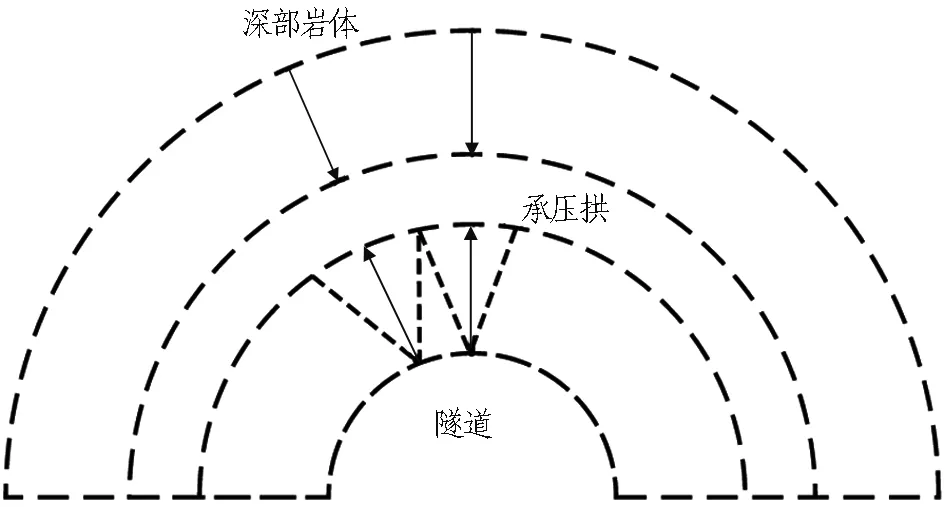
图15 让压锚杆的支护原理

如上文所述，大尺度让压锚杆在杆体受拉阶段可以提供更高的支护力稳定围岩，张彪等[16]在毛羽山隧道进行的现场试验也初步证明了这点。围岩变形一定程度后，让压锚杆“以支为主”，更高的支护压力有利于约束围岩变形，稳定围岩。传统的让压锚杆，后期无法提供更高的支护力，只能在围岩荷载降低到让压力之下才能稳定围岩，仅实现了“边支边让”的支护理念。利用大尺度让压锚杆，可以在一定的让压量后锁定杆体，利用杆体受拉阶段，真正实现“先柔后刚”的支护思想，如图16所示。传统让压锚杆让压力保持恒定，为了保证最终能够有效稳定围岩，让压力一般较大； 而大尺度让压锚杆后期支护力可大幅增加，所以让压力只需大于下限值即可，围岩变形初期，合适的让压力有利于充分释放围岩变形，围岩变形后期，高支护力有效约束围岩，真正实现让压锚杆“边支边让，先柔后刚”的支护理念，减小围岩变形量，有利于隧洞的长期稳定。

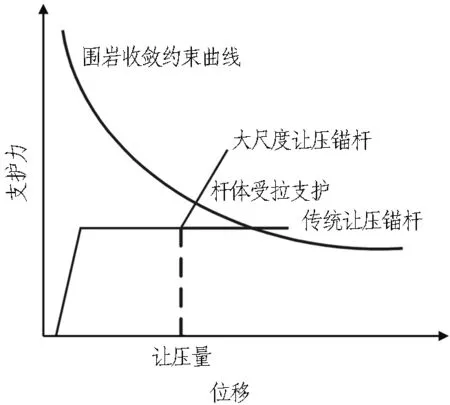
图16 大尺度让压锚杆支护曲线

Fig. 16 Support curve of yielding anchor bolt with large allowable deformation

6 结论与讨论

1)大尺度让压锚杆工作分弹性变形、滑动让压和杆体受拉3个阶段。滑动让压阶段让压力稳定，杆体受拉阶段杆体屈服强化，可以提供更高的支护力，2阶段杆体工作性态不同，塑性发展水平有显著差异。

2)让压锚杆让压力存在下限值。当支护力超过地应力的40%时，隧洞收敛比基本低于5%，可以有效控制围岩变形。岩体抗压强度越高，支护力的下限值越低。工程应用时应确保让压支护力大于下限值。

3)让压量增加到一定水平后，再增加相同的让压量，二次衬砌受到的压力降幅减小。让压量应适当，利用让压锚杆杆体支护阶段更高的支护力，真正实现“边支边让，先柔后刚”的支护理念，有利于隧洞长期稳定。

4)多数软岩挤压性大变形流变现象显著，让压量的合理确定应考虑软岩的蠕变效应，需结合具体工程进一步研究； 让压锚杆让压时，与其他支护措施的协同工作问题也有待后续研究。

7 致谢

图强工程材料公司王勇高级工程师为本文大尺度让压锚杆研究提供了相关资料，在此表示衷心感谢！

[1] 孙钧，潘晓明，王勇. 隧道围岩挤入型流变大变形预测及其工程应用研究[J]. 河南大学学报(自然科学版), 2012(5): 646-653. (SUN Jun, PAN Xiaoming, WANG Yong. Study of the prediction of large squeezing creep-deformation of tunnel surrounding rocks & its application[J]. Journal of Henan University (Natural Science),2012(5): 646-653. (in Chinese))

[2] Hoek E. Big tunnels in bad rock[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(9): 726-740.

[3] Hoek E, Guevara R. Overcoming squeezing in the Yacambú-Quibor Tunnel, Venezuela[J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 389-418.

[4] Cantieni L, Anagnostou G. The interaction between yielding supports and squeezing ground[J]. Tunnelling and Underground Space Technology, 2009, 24(3): 309-322.

[5] 王襄禹，柏建彪，李伟. 高应力软岩巷道全断面松动卸压技术研究[J]. 采矿与安全工程学报, 2008, 25(1): 37-40, 45. (WANG Xiangyu, BAI Jianbiao, LI Wei. Stress-relief technique of full-face gangue dropping in soft rock roadway under high stress[J]. Journal of Mining & Safety Engineering, 2008, 25(1): 37-40, 45. (in Chinese))

[6] FENG X T, QIU S. Tunnelling and underground construction in China: Challenges and progress[C]// ISRM International Symposium: 8th Asian Rock Mechanics Symposium. Sapporo: ARMS, 2014: 23-34.

[7] 何亚男. 可拉伸锚杆的基本原理与设计[J]. 矿山压力,1987(2): 16-19,2. (HE Yanan. Basic principle and design of yielding bolt[J]. Mining Pressure,1987(2): 16-19, 2. (in Chinese))

[8] CAI M, Champaigne D. Influence of bolt-grout bonding on MCB conebolt performance[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 49(1): 165-175.

[9] Ansell A. Laboratory testing of a new type of energy absorbing rock bolt[J]. Tunnelling and Underground Space Technology, 2005, 20(4): 291-300.

[10] 吴学震，王刚，蒋宇静，等. 拉压耦合大变形锚杆作用机理及其试验研究[J]. 岩土工程学报, 2015(1): 139-147. (WU Xuezhen, WANG Gang, JIANG Yujing, et al. Mechanism of CTC-yield bolts and its experimental research[J]. Chinese Journal of Geotechnical Engineering,2015(1): 139-147. (in Chinese))

[11] 连传杰，徐卫亚，王志华. 一种新型让压管锚杆的变形特性及其支护作用机理分析[J]. 防灾减灾工程学报,2008(2): 242-247. (LIAN Chuanjie, XU Weiya, WANG Zhihua. Analysis of deformation characteristic and supporting mechanism of a new-typed yielding anchor bolt[J]. Journal of Disaster Prevention and Mitigation Engineering, 2008(2): 242-247. (in Chinese))

[12] Varden R, Lachenicht R, Player J, et al. Development and implementation of the Garford dynamic bolt at the Kanowna Belle Mine[C]//10th AusIMM Underground Operators’ Conference 2008: Boom and Beyond Proceedings. Launceston: Australasian Institute of Mining and Metallurgy, 2008: 95-102.

[13] WU R, Oldsen J, Lamothe M. The Yield-Lok bolt for bursting and squeezing ground support[C]//Proc. 5th Int. Seminar on Deep and High Stress Mining, Santiago. Chile: Australian Centre for Geomechanics, 2010: 301-308.

[14] LI C C. A new energy-absorbing bolt for rock support in high stress rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3): 396-404.

[15] 何满潮，李晨，宫伟力，等. NPR锚杆/索支护原理及大变形控制技术[J]. 岩石力学与工程学报, 2016(8): 1513-1529. (HE Manchao, LI Chen, GONG Weili, et al. Support principles of NPR bolt/cables and control techniques of large deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(8): 1513-1529. (in Chinese))

[16] 张彪，张志强，汪波，等. 让压锚杆在大变形隧道支护应用中试验研究[J]. 岩土力学, 2016(7): 2047-2055. (ZHANG Biao, ZHANG Zhiqiang, WANG Bo, et al. Experimental study of application of yielding bolt to large deformation tunnel[J]. Rock and Soil Mechanics, 2016(7): 2047-2055. (in Chinese))

[17] 孙钧，潘晓明，王勇. 隧道软弱围岩挤压大变形非线性流变力学特征及其锚固机制研究[J]. 隧道建设, 2015,35(10): 969-980. (SUN Jun, PAN Xiaoming, WANG Yong. Study of non-linear rheologic mechanical property of squeezing deformation of soft surrounding rock in tunneling and its anchorage mechanism[J]. Tunnel Construction,2015, 35(10): 969-980. (in Chinese))

[18] 郭永建，姜飞，周浩，等. 新型让压锚杆作用机理研究[J]. 力学与实践, 2015(2): 193-196,237. (GUO Yongjian, JIANG Fei, ZHOU Hao, et al. The mechanism of the new-type of yielding bolt[J]. Mechanics in Engineering, 2015(2): 193-196, 237. (in Chinese))

[19] 项小珍，吕志平， 吴航通， 等. 中空注浆让压锚杆: CN

201220593344.4[P]. 2013-04-24[2016-09-19]. (XIANG Xiaozhen, LYU Zhiping, WU Hangtong, et al. Hollow grouting yielding bolt: CN201220593344.4[P]. 2013-04-24[2016-09-19]. (in Chinese))

[20] Hoek E, Marinos P. Predicting tunnel squeezing problems in weak heterogeneous rock masses[J]. Tunnels & Tunnelling International, 2000, 32(11): 45-51.

[21] Panthi K K, Nilsen B. Uncertainty analysis of tunnel squeezing for two tunnel cases from Nepal Himalaya[J]. International Journal of Rock Mechanics and Mining Sciences， 2007, 44(1): 67-76.

[22] 张传庆，周辉，朱勇，等. 基于潜在挤压比的地下工程软岩挤压程度评价方法研究[J]. 岩石力学与工程学报，2016(5): 939-947. (ZHANG Chuanqing, ZHOU Hui, ZHU Yong, et al. An evaluation method of squeezing degree based on potential squeezing ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(5): 939-947. (in Chinese))

[23] 潘晓明. 挤压大变形隧道围岩流变力学特征研究[D]. 上海: 同济大学, 2011. (PAN Xiaoming. Study of large squeezing deformation rheological mechanical characteristics of tunnel surrounding rocks[D]. Shanghai: Tongji University, 2011.(in Chinese))

[24] 陈东方，冯夏庭，徐鼎平，等. 砂浆锚杆加固效果的等效数值模拟方法研究[J]. 岩土力学,2015(4): 1195-1204. (CHEN Dongfang, FENG Xiating, XU Dingping, et al. An equivalent numerical method for evaluating the reinforcing effectiveness of grouted bolts[J]. Rock and Soil Mechanics, 2015(4): 1195-1204. (in Chinese))

[25] 公路隧道设计细则: JTG/T D70—2010[S]. 北京: 人民交通出版社,2010. (Guidelines for design of highway tunnel: JTG/T D70—2010[S]. Beijing: China Commu-nications Press, 2010. (in Chinese))

Study of Performance and Application of Yielding Anchor Bolt with Large Allowable Deformation

YANG Yusheng1, 2

(1.DepartmentofGeotechnicalEngineering,TongjiUniversity,Shanghai200092,China;2.KeyLaboratoryofGeotechnicalandUndergroundEngineering(TongjiUniversity),MinistryofEducation,Shanghai200092,China)

The large squeezing deformation of soft rock can not be ignored under the rapid development of tunnel construction. As a result, yielding anchor bolt becomes more and more important in large deformation control. The structure and support mechanism of a new type of yielding anchor bolt with large allowable deformation are introduced. And then the performances of the anchor bolt during elastic deformation phase, sliding yielding phase and tensile phase are verified by ANSYS software. Finally the yielding pressure and yielding deformation of the anchor bolt are analyzed by probit analysis based on Hoek formula and ABAQUS software respectively. The results show that: 1) The lower limit exists in yielding pressure of the anchor bolt; and the higher the compressive strength of rock mass is, the smaller the lower limit of anchor bolt is. 2) The decreasing amplitude of secondary lining decreases when the yielding deformation of anchor bolt reaches a certain value. The concept of “supporting while yielding and flexible support goes first and then rigid support” can be realized; large deformation of surrounding rocks can be controlled effectively; and the long-term stability of the tunnel can be improved during the tensile phase of yielding anchor bolt with large allowable deformation.

yielding anchor bolt with large allowable deformation; large deformation of soft rock; Hoek formula; yielding pressure; yielding deformation

2016-09-19;

2016-11-22

杨喻声(1993—)，男，重庆忠县人，同济大学土木工程专业在读博士，研究方向为隧道及地下结构。E-mail： ysyang@tongji.edu.cn。

10.3973/j.issn.1672-741X.2017.03.010

U 455.7+2

A

1672-741X(2017)03-0321-09