降板对现浇板受力性能的影响

陈洁瑜 周文琪

(艾奕康设计与咨询(深圳)有限公司上海分公司 上海 200082)

降板对现浇板受力性能的影响

陈洁瑜 周文琪

(艾奕康设计与咨询(深圳)有限公司上海分公司 上海 200082)

现浇板降板是工程中的常见的构造。为研究降板后楼板的受力性能，利用sap2000，建立6个不同降板高度的模型。对比各模型现浇板在不同方向上的内力分布状态，得到现浇板随着降板高度的变化引起的楼板内力分布变化的规律。对比不同模型降板交界处的内力状态，得到不同降板高度下的降板交界处构造的内力变化规律，并基此提出设计建议。

降板;楼板内力;边界条件

1 概述

现浇板是钢筋混凝土结构的基本构件。大多数的现浇板四周都支承于混凝土梁上。但由于建筑功能的需要，部分如在卫生间、厨房等位置的现浇板需要作降板处理。由于降板处理后的现浇板的不同部位之间存在高差，其受力状态与平板相比会发生相应的改变。

现浇板的受力状态的主要影响因素，包括现浇板的位置，长宽比，板边界的支承形式，相邻梁柱刚度以及相邻板格间的荷载布置等。根据现浇板的几何特性，板厚h与中面特征尺寸l之比大致在1/100～1/ 80≤h/l≤1/5或1/8之间的板，可按照薄板理论进行分析设计［1］。因此对于一般混凝土结构中的大部分现浇板，都可以按照薄板理论进行计算设计。根据Kirchhoff－Love假定，薄板在变形前垂直中面的任一直线，在薄板变形后仍然保持为直线，且长度不变;薄板中面的正应力可以忽略不计;薄板内无剪切变形和伸缩变形。因而对现浇板的设计可以忽略平面外的刚度，从而使设计过程得到相应的简化。

现浇板的另外一种计算方法是屈服线法。它是通过假定板的极限荷载是通过一种与边界条件相协调的破坏机构来估算的。它是一种上限方法，即在板上假定板的塑性较线的分布，塑性铰线上的力矩是界面的极限抵抗力矩，而极限荷载是根据虚功原理或者平衡方程确定的。对于这种方法，也是假定板的剪切刚度足以防止板的剪切破坏。

根据基于薄板理论［2］板带法和屈服线法。对于单向板(长宽比大于2m～3m)，在短跨方向取单位板宽的现浇板，等代梁的方法进行配筋设计。而对于四边固接的双向板(长宽比小于2m～3m)，则将现浇板自角部按45°角进行划分，根据划分的区域进行内力计算，求取相应的内力后，进行现浇板的配筋设计。

根据现浇板的设计理论，折板构造对现浇板主要有以下3方面影响:

(1)对本块板内传力路径的影响

折板并非连续的板，在垂直折板边方向上，板上的弯矩的传递受到影响，板无法等效成一般的梁或者屈服线划分形成的板块。

(2)对边界条件以及相邻楼板传力的影响

折板使降低后的板与周围的现浇板存在高差，从而使得降低后的板与四周板的弯矩传递受到影响。

(3)改变现浇板的长宽比

在降板后，原本完整的现浇板实际上等同于两块板，中间依靠一根等同于梁的肋进行连接。

针对降板结构，目前相关混凝土结构设计规范中并未给出相关的条文，只有《混凝土结构施工图平面整体表示方法制图规则和构造详图》(11G101－1)［3］中给出了相关的构造形式，如图1所示。在实际利用如pkpm，yjk等一般结构分析软件进行设计的工程中，由于软件功能的限制，往往将结构有降板构造的板与相邻板的边界条件设置为简支边，不传递弯矩，实际配筋也只是按照构造要求进行配置，而板内仍然按照没有降板的受力状态进行设计。

为明确降板构造对现浇板受力的影响，需要对相关构造进行研究。

图1 折板构造详图

2 模型建立

为对比不同降板高度对现浇板受力的影响，在sap2000中建立的3榀3跨的单层框架结构，如图2所示。

梁板柱混凝土等级均为C30，柱网间距均为6m，柱截面尺寸为0.4m×0.4m，梁截面尺寸为0.3m× 0.6m。在板面施加6kN/m2的均布荷载。将框架中部的5#板格划分成5a#板格和5b#板格。在模型中对5a#板格作降板处理。分别按照不同的降板高度分别建立model1－mdel6，具体降板高度，如表1所示。

表1 不同模型降板高度

图2是模型平面图。模型中，梁柱均采用线单元建立，现浇板采用符合Kirchhoff－Love假定的薄板单元建立，降板区域连接不同标高的两块板的肋采用壳单元模拟。在降板标高上建立围着5#板格的四根梁，以支撑低标高的板格。将每块板划分成1m×1m的单元模型，如图3所示。

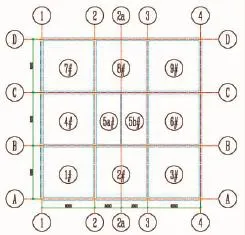
图2 模型平面图

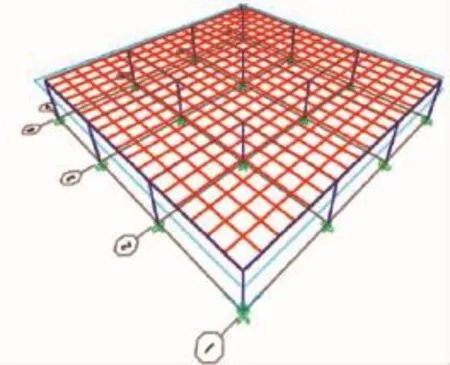
图3 mdel1 sap2000模型

3 降板对沿降板方向板内力分布的影响

3．1 未降板结构板内力

Model1沿着降板方向的现浇板绕 y轴的弯矩M11的内力云图，如图4所示。可以明显地观察到板端的负弯矩区域和板跨中的正弯矩区域。提取MODEL1的楼板中间板带内力数据，如表2所示。

表2 model1支座跨中弯矩(kN·m)

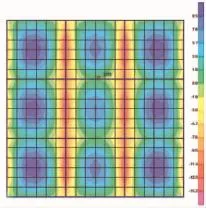
图4 MODEL1板M11图

(1)现浇板边支座的弯矩小于中间跨支座上的弯矩。如A－B轴线当中的1#，2#，3#三块板，1#板1轴支座上绕y轴上的弯矩为－8．46kN·m，而中间跨2轴支座上的弯矩则达到了15 kN·m左右。这是由于边跨支座处没有现浇板与楼板相连，楼板的边界条件近似为简支，而中间跨支座处相邻板跨有楼板相连，楼板支座近似于固接。板跨内的弯矩偏向于固接端，使中间支座上的楼板弯矩偏大。同理查看其它板跨也得到相同的规律，如图5所示。需要注意的是，此处的简支并非绝对简支，梁对现浇板的约束依然存在，因此在端支座上，现浇板的弯矩依然存在［4］。

图5 MODEL1板M22图

(2)现浇板边跨跨中弯矩大于中间跨跨中弯矩。如1#，2#及3#板中，1#板绕 y轴的跨中弯矩为10．6kN·m，2#板绕y轴的跨中弯矩为8．9kN·m。这是由于1#板在1轴的支座简支，在2轴的支座固接，而2#板在2轴和3轴的支座上都为固接。边界条件的不同使得现浇板在支座上的弯矩分布发生变化，导致各板块跨中的内力分布发生变化。固接端的存在减小了楼板跨中的弯矩值。

3．2 降板边平行于y轴时，各模型绕y轴M11弯矩分布的对比

如图6所示，x轴为0的位置为降板分割线位置，即图2中的2a轴位置。根据图6可以发现:

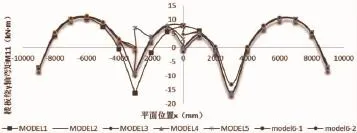
图6 各模型中间榀楼板M11内力对比

(1)各模型在平面位置 x处于 －9 000mm～－6 000mm范围内的现浇板内力几乎相同，因此降板对这部分楼板的内力影响不大。这是由于降板主要造成了楼板边界条件的变化，而降板区域与这部分楼板的距离相对较远，因此其影响程度有限。同理各模型在x处于3 000mm～9 000mm(3－4轴)范围内现浇板的内力状态也相互接近。

(2)在x处于－6 000mm～－3 000mm范围内，正弯矩区段MODEL1的楼板内力小于降板或未设置现浇板的模型，而在－3 000mm位置处，MODEL1的内力大于其余模型。这是由于在5a#板块降板后，5a#与4#楼板之间的边界条件由固接逐渐变为简支。支座约束条件的减弱，使得降板模型在该范围内的弯矩小于MODEL1。

(3)在 x处于 －3 000mm降板边界位置处(2轴)，在4#板板格一侧，由于降板后边界条件的改变，支座负弯矩端弯矩由MODEL1的－16．16kN·m降低至其他模型的－10．1kN·m左右。而5a#板格左侧楼板弯矩也随着降板高度的增大而逐渐减小。在降板高度为350mm时，该处弯矩由负弯矩变为了正弯矩。这是由于随着降板高度的增大，降板交界面上如图1所示的构造的交接肋的高度随之增高。当肋的刚度逐渐增大，将其等效为梁连接，该等效梁在竖向荷载的作用下会在跨中位置产生正弯矩，从而得到MODEL5的内力结果。因此，设计过程中需要考虑降板边界上楼板弯矩的存在，分别对楼板及边界上的肋进行抗弯承载力验算。

(4)当x为－3 000mm至3 000mm时，MODEL15#板在x=0处(2a轴)的弯矩值最大。在5a#板降板后，各降板模型x为－3 000mm至0mm区段及0mm至3 000mm区段分别出现一个内力峰值。这是由于降板的存在，近似地将一整块板分割成为了两块单独受力的板。各降板模型在x等于0mm处的弯矩均较小，有的模型甚至趋近于0，说明降板边界对楼板的约束是相当的弱。由于支座约束的减弱，降板模型的负弯矩区域范围小于未降板模型，但正弯矩区域大于未降板模型。在x=－3 000mm至0mm区域内降板模型正弯矩峰值并不小于未降板模型。由于5B#板为非降板区域，x=0mm至3 000mm区域内降板模型正弯矩峰值与未降板模型差距并不明显。

如图7和图8所示，同时综合图6，4a#板的受力状态随着降板高度的增大而逐渐趋于一块独立的板的受力状态，而降板的变高差处也相应成为新划分板格的支座。该支座也相应成为5b#板格的支座。

综合降板区域现浇板的内力分析，分别按照整板和两块单独的板对现浇板进行包络设计，且确保足够的通长底筋，保证降板构造的承载能力。

表3 边榀板内力分布kN·m

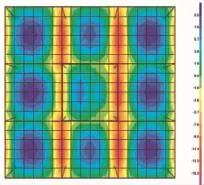
图7 MODEL5板M11图

(5)由于5B#板块未降板，各模型的边界条件并未发生较大的改变。因此各模型在x大于3 000mm区段内的内力分布较为相近。

(6)边榀的内力状态，如表3所示，各模型边榀框架内现浇板的绕y轴弯矩M11分布基本接近。这是由于降板的构造只对降板区域周边的部分楼板的边界条件发生有限的影响。因此降板构造对相邻楼板在M11方向的内力分布影响不大。故在进行降板区域周边的现浇板设计时，可忽略降板对周边楼板该方向内力的影响。

3．3 降板边平行于y轴时，各模型绕x轴M22弯矩分布的对比

图9所示为未降板部分楼板在2a轴上绕x轴弯矩M22弯矩分布，图10所示为5a#楼板在2a轴上绕x轴弯矩M22弯矩分布。边榀的各板绕x轴弯矩M22如表4所示。由图9及表4可以发现:

(1)与M11的分布类似，对比图9与表4，各模型y在－9 000mm～－4 000mm及4 000mm～9 000mm (A－B及C－D边榀外侧2/3)范围内的现浇板内力相近，同样说明降板对周边现浇板在绕x轴方向的弯矩影响有限，因此在对周围现浇板y轴方向配筋时，可忽略降板的影响。

图8 MODEL5－5a#板M11图

(2)在－3 000mm及3 000mm处(B轴和C轴)支座弯矩随着降板高度的增大而增大，但无现浇板时，该处的弯矩较MODEL1小。说明降板引起现浇板弯矩分布不均匀造成了局部内力的增大。

(3)对于y在－3 000mm～－3 000mm位置区域(B－C轴)，MODEL1所示为一条只有一个在0位置处的峰值，但是其他降板的模型中却分别在－2 000mm，0mm，2 000mm位置处出现了3个峰值，且峰值随着降板高度的增大而增大，3个峰值的大小也相互接近。对于MODEL6，由于该处为5b#板的支座，因此内力与其他模型又有很大不同。如图11所示，现浇板在5b#区域发生了重分布，形成了多个内力中心。

产生这种现象的主要原因是由于由于降板区域和未降板区域内力传递的变化造成的。如图11～图12所示，未降板区域正弯矩范围明显大于未降板区域，而这种变化的产生主要通过如图13所示的连接两块板之间的肋实现。这道肋的存在近似等效成为一根梁，对现浇板形成一定的约束。未降板区处于肋的的顶部，降板区域处于肋的底部，分别起到加强梁顶与梁底的作用。如图13所示，竖向荷载作用下，梁顶的正应力区域明显大于梁底，从而造成了梁顶内力分布的变化。

(4)由图10可以发现，各模型对应的降板处的内力分布均较为相近，但在支座端，支座边界条件的改变，降板处的现浇板内力会较未降板部分的现浇板的内力小，但正弯矩处弯矩有所增加。因此，建议分别按简支及固接两种方式，分别计算整板和单独的降板内力，并取大值。由于弯矩在降板区域内仍要传递，因此要保证钢筋在降板区域内的连续性。

图9 各模型中间榀未降板部分楼板M22内力对比

图10 各模型中间榀降板部分楼板M22内力对比

表4 边榀板内力分布kN·m

图11 MODEL5板M22图 图12MODEL5－5a#板M22图

图13 MODEL5－5a#5b#板交界处M22图

4 折板构造处肋的受力性能

如前文所述，降板交界处板肋受力可等效为一根梁，如图13所示，为MODEL5的5a#与5b#交界处楼板构造的内力云图。可以发现，该位置的构造呈现出受弯构件的受力形态。在内力计算时，建议按梁构造对降板区域进行验算，并配置相应的抗弯、抗剪及抗扭钢筋。特别是由于建筑功能的需要，部分降板区域需要做面层回填处理，使降板区域荷载过大，引起改肋梁内力过大时，需要对该构造特别关注。

5 结论

通过对比分析各不同降板高度模型的楼板内力分布，可以得到以下结论:

(1)楼板降板主要对降板板格的内力有较大影响，对与降板板格相邻的楼板的内力分布影响不大。因此在设计过程中，可忽略降板构造对降板区域周边现浇板的影响。

(2)随着降板高度的增大，楼板的受力状态逐步变成由降板交界处分割而成的两块板，但是由于边界条件并未达到完全的简支或者固接，并不能完全等同于独立的两块板。两者之间的内力依然存在相当大的关联。建议在进行设计时，分别按照整体和局部、固接和简支对楼板进行包络设计，保证楼板的承载力。

(3)随着降板高度的增大，楼板降板边界上的肋的受力状态趋近于一根支撑两块板的梁。建议在设计过程中，按梁对该构造进行验算，并配置相应的钢筋，使其满足承载力要求。

［1］ 卓卫东．应用弹塑性力学［M］．北京:科学出版社，2004．

［2］ R·Park，W·L·Gambe．钢筋混凝土板［M］．上海:同济大学出版社，1992．

［3］ 中国建筑标准设计研究院．混凝土结构施工图平面整体表示方法制图规则和构造详图(11G101－1)［S］．北京:中国计划出版社，2011．

［4］ 蒋利学．竖向荷载下现浇梁板协同工作对楼板的影响［C］//第19届全国结构工程学术会议论文集．2010．

The Influence of Descending Plate Impacting on Monolithic Slab

CHEN Jieyu ZHOU Wenqi
(AECOM Technology Corporation，Shanghai 200082)

Descending plate is common structure in structural engineering．To study the force distribution of descending plate，6 finite models of different descending depth are built with Sap2000．Comparision of force distribution situations of different models are made to analysis how the descending depth impact on the force distribution of the slab．Comparison of force distribution situations of different models at the descending boundary is also made to analysis how the descending depth impact on the force distribution of the boundary．Some advices for design are proposed．

Descending slab;Slab force;Boundary condition

TU3

A

1004－6135(2017)02－0045－05

陈洁瑜(1983．4－ )，女，工程师。

E-mail:Jieyu．chen@aecom．com

2016－11－21