测量数据的科学处理及其在工程测量中的应用研究

杨武

（莆田学院 机电工程学院，福建 莆田 351121）

测量数据的科学处理及其在工程测量中的应用研究

杨武

（莆田学院 机电工程学院，福建 莆田 351121）

人们通常会用均值法(算术平均法)或统计法来处理测量数据,统计法处理测量数据虽然比均值法能多给出数据处理结果可信度，但是,用一个实数仍然不能表示多个实测值及其可信度.本文应用未确知数学处理测量数据则可克服这些方法的不足.

测量数据处理；未确知数学

1 不确定性与未确知数学

任何一个工程测量量，在多次测量中，得到的测量值一般都不是一样的，换句话说，任何一个待测的物理量都是一个未确知量，存在有不确定性.自然界的现象有两大类：一类是确定性现象，一类是不确定性现象.研究确定性（或称必然性）现象的数学工具是经典数学（包括初等数学和以微积分为基础的高等数学）.对于不确定性现象，人们最早接触的是随机性.研究随机性的数学工具是概率论和数理统计[1].与随机性不同的第二类不确定性是模糊性，处理模糊性的数学工具是模糊数学[2].他是美国加利福尼亚大学自动控制专家查德（L.A,Zadeh）教授于1965年创立的.80年代初，我国学者，邓聚龙教授为研究灰性而提出灰色系统理论[3].灰性是一种不确定性程度比随机性和模糊性更高的第三类不确定性.而被王光远院士称为“未确知性”的是不同于随机性，模糊性和灰性的第四类不确定性[4].这种不确定性主要不在于事物本身，而是由于人们不能完全把握事物的真实状态和数量关系造成的纯主观认识上的不确定性.研究这类不确定性的数学工具是1990年确立的未确知数学[5].

2 未确知有理数

未确知有理数是未确知数学中的最基本、最简单、应用最广、使用方便的未确知数.它是实数的一种推广，能精细地刻划和表达客观世界中许许多多的“未确知量”.

2.1 未确知有理数的定义

对任意闭区间[a，b]，a＜x1＜x2＜…＜xn=b，若函数φ (x)满足：

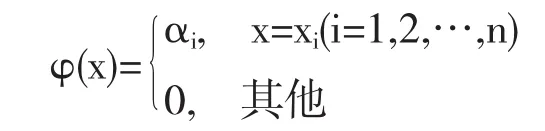
2.2 未确知有理数的四则运算

设未确知有理数A,B分别为

2.2.1 可能值带边和矩阵

表1称为A与B的可能值带边和矩阵，由小到大的实数列x1，x2，…，xk和y1，y2，…，ym分别称为A与B的可能值序列.

2.2.2 可信度带边积矩阵

表2称为A与B的可信度带边积矩阵，f(x1)，f (x2)，…，f(xk)和g(y1)，g(y2)，…，g(ym)分别称为A与B的可信度序列.

表2

2.2.3 未确知有理数的四则运算

将A与B的可能值和矩阵中的元素，按从小到大的顺序排成一列:x1，x2…xl，其中相同的元素算作一个.A与B的可信度积矩阵中与xi(i=1,2,…l)相对应的元素排成一个序列:k1，k2…kl.其中若xi表示A与B的可能值和矩阵中M个相同元素时，ki表示这M个相同元素在A与B可信度积矩阵中的M个相应元素之和.那未确知有理数[[x1,xl],φ(x)]为A与B之和，记作A+B，其中

对于A与B的减法A-B,乘法A×B和除法A÷B运算，只需把加法运算中的可能值带边和矩阵中的“和”分别改为“差”、“积”、“商”，便可把可能值带边和矩阵分别变为可能值带边差矩阵、积矩阵和商矩阵，其他一切不变，即可分别得到未确知有理数差的运算A-B，积的运算A×B以及商的运算A÷B.

3 未确知有理数在测量数据处理中的应用

3.1 测量数据的未确知有理数表达

为说明问题方便起见，以大学物理实验中的长度测量为例：用游标卡尺测量一钢珠直径，得到5次重复测量结果：14.90，9.80，8.82，8.82，7.66（mm）.由均值法得到钢珠的直径为10.00mm.

均值法是处理测量数据的一种基本方法.它在一定程度上可减小测量中的随机误差，而且结果为一实数，使用方便.但是，用均值法近似表示一个物理量的测量结果，到底有多大的可信度却是不清楚的.让我们回过头来看上述例子，如果我们认为钢珠直径在5次测量中，得到一次14.90mm的主观可信度为1/5，则9.80mm和7.66mm的可信度也分别为1/5，而8.82mm的可信度则为2/5.于是钢珠的直径测量值落在区间 [7.66，9.80]的可信度就高达80%，而均值法认为钢珠直径的近似值为10.00mm的可信度则不会超过20%.

由此可见，用一个实数来表示一个物理量（如上例中的钢珠直径）的测量结果就难免失真.事实上，任何一个实数都无法表示多个实测值，也无法表示每一次测量结果的可信度.而未确知有理数则可以克服这一不足，如上述钢珠直径的测量结果可表示为一个四阶的未确知有理数：

用未确知有理数[[7.66,14.90],φ(x)]与用一个实数D=14.00mm表示钢珠直径的根本不同点在于：未确知有理数能把我们所获得的全部信息无遗漏、无失真的表示出来.特别是，用它参与运算可减少误差积累，可最大限度地用足已知条件.这些都是未确知有理数处理测量数据的优点.

值得一提的是，在物理量的测量中，除了纯主观认识上的不确定性以外,还会受到测量仪器精度、测量次数、测量者的经验和操作能力等的影响.因此，所要测试的所有物理量都是“未确知量”.这就需要用未确知有理数来表达测量结果,以避免信息遗漏、失真，并应用未确知数学来处理实验数据，以减少误差积累.

3.2 测量数据的未确知有理数处理

同样，为说明问题方便起见,以大学物理实验中的小圆柱体体积测量和数据处理为例，用游标卡尺测小圆柱体的直径D，高度H各4次，测量的结果如表3所示.

表3 单位:mm

以上小圆柱体的直径和高度的测量结果可分别表示为未确知有理数D和H:

由未确知有理数的四则运算，得：

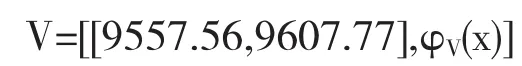
对以上结果，作如下分析：

(1)当x=9584.80时，可信度等于0.188，为最大值.作为一个测量的可信度能达到0.188，可认为是很大的.显然小圆柱体的体积是一个确定值，因此，可认为该圆柱的体积应在这一数值附近.

(2)若以可信度最大的x值为中心，向上向下各取3个值，即向上取值到9575.35，向下取值到9594.25，此时小圆柱体的体积落在区间[9575.35，9594.25]上的可信度将达到75%.由此可认为小圆柱体的体积应在该区间内.若取上述7个数的平均值9583.64mm3作为小圆柱体的体积是合理的，也是符合实际的.

(3)当实测数据更精确时，计算结果也将会更准确.

4 结论

工程测量中所有的测量量都是“未确知量”，应用未确知数学来处理未确知量,不仅可以确保测量获得的全部信息无遗漏、无失真，而且用它进行运算还可减少误差积累，最大限度的用足全部测量结果.

〔1〕祝东进，郭大伟，刘晓.概率论和数理统计[M].北京:国防工业出版社,2010.

〔2〕谢季坚，刘承平.模糊数学方法及其应用[M].武汉:华中科学技术出版社,2013.

〔3〕刘洪.新学科精览[M]北京:中国科学技术出版社,1990.290-302.

〔4〕王光远.论未确知信息及其数学处理[J].哈尔滨建筑工程学院学报,1990(4).

〔5〕刘开第，吴和琴，庞彦军，等.不确定性信息数学处理及应用[M].北京:科学出版社,1999.48-71.

TV221.1

A

1673-260X（2017）03-0081-03

2016-12-23

福建省教育厅教育教学改革研究项目：测量数据的科学处理与实践(JAS151326)