变参数螺旋弹簧刚度特性研究

聂 维， 雷强顺， 陈轶杰， 高晓东， 桂 鹏

(中国北方车辆研究所，北京100072)

变参数螺旋弹簧刚度特性研究

聂 维， 雷强顺， 陈轶杰， 高晓东， 桂 鹏

(中国北方车辆研究所，北京100072)

以油气弹簧的刚度特性为参考，借鉴离散化的思想并结合螺旋弹簧的理论知识，建立变参数螺旋弹簧压缩过程的数学模型.结合实际车辆装配尺寸，通过编制Matlab程序对变参数螺旋弹簧的参数进行解析计算.并将变参数螺旋弹簧刚度曲线与油气弹簧的刚度特性曲线相比较，结果表明变参数螺旋弹簧的刚度特性可以接近油气弹簧的刚度特性.

螺旋弹簧；变参数；刚度特性

悬架系统的性能对车辆乘坐舒适性有着很大的影响，其作用是传递作用在车轮和车架之间的力和力矩，缓冲行驶过程中由路面不平引起并传递给车架或车身的冲击力，衰减由此引起的振动，以保证汽车平顺地行驶.对于载荷变化很大的重型车辆，悬架系统中弹性元件最理想的刚度特性曲线为强非线性，目前普通独立悬架虽然在可变阻尼力减振器和螺旋弹簧的配合下能体现一定的非线性，但远不能保证车辆在各个工况下表现良好的舒适性和安全性.为得到理想的刚度特性，某型装甲车悬架系统采用了油气弹簧，油气弹簧以惰性气体充当弹性元件，可以实现弹性元件的强非线性，但出于控制成本和拓展车辆全温域适应性的目的，通过设计使变参数螺旋弹簧-减振器的悬架型式和油气弹簧能够实现完全互换.变参数螺旋弹簧有着独特的非线性特性，这种特性使它能更好地适用于各种复杂的路况.

因此，在一些高性能汽车的悬架上，变参数螺旋弹簧得到了广泛的应用.例如德国MAN10t重型越野车、美国高机动多用途轮式车(HMMWV)系列车型均采用了变参数螺旋弹簧.螺旋弹簧主要参数包括簧丝直径d、簧圈中径D、节距t及螺旋角α.普通圆柱螺旋弹簧的所有结构参数均为定常数；参数随着簧丝长度l变化的弹簧称为变参数螺旋弹簧.变参数螺旋弹簧有不等节距圆柱螺旋弹簧、截锥螺旋弹簧以及组合螺旋弹簧，等等.这类螺旋弹簧的载荷与变形呈非线性关系，这种特性使它能更好地适用于各种复杂的路况，当路面较平坦时，弹簧的刚度较小；而当路面的起伏较大时，弹簧的刚度随之增大.同时，弹簧刚度的变化也可有效避免汽车在行驶过程中出现共振现象，从而提高了汽车的乘坐舒适性.可以预见，变刚度圆柱螺旋弹簧将是今后车用弹簧的一个重要发展方向[1].现阶段对变参数螺旋弹簧的设计和应用仅限于变节距或变中径的单参数变化，其只有弱非线性刚度特性无法拟合为油气弹簧的刚度特性，因此本研究只对多参数变化的变参数螺旋弹簧刚度进行解析计算.

1 理想刚度特性曲线讨论

油气弹簧由气室和油室组成，油气之间用浮动活塞对油气进行隔离，气体作为弹性元件，油液作为传力介质.随着活塞运动气体的体积也会被压缩，气体对活塞表面的压力随之变大从而实现油气弹簧的非线性刚度特性.利用悬架部件试验台对某型车悬架系统中油气弹簧的刚度特性进行试验分析，得到油气弹簧刚度特性曲线，如图1所示.

图1 油气弹簧弹性元件刚度特性

该弹簧在静平衡位置A点处附近时刚度较小且增加平缓，能够保证车辆的舒适性；当车轮行程增加，弹簧位移到达B点时，弹簧的刚度增加明显，保证了车辆行驶的稳定性.利用油气弹簧的这种特点可以保证车辆在各种工况和路面上都能保证良好的舒适性和安全性.因此，油气弹簧的强非线性刚度特性是高机动重载车辆理想特性曲线.但与螺旋弹簧-减振器悬架系统相比，油气悬架系统的成本昂贵并且对工作温度要求较高，所以设计一种变参数螺旋弹簧近似贴合油气弹簧弹性元件的刚度特性成为重要的课题.

2 变参数螺旋弹簧理论分析

对于中径变化的螺旋弹簧，采用离散式定义的方法，将每一段的螺旋弹簧用简单、基础形状，如圆柱形进行描述，通过对每一段弹簧的参数进行计算后，然后将每一段弹簧串联积分计算成一个复杂的、合理的螺旋弹簧.对于变簧丝直径的螺旋弹簧，为了简化设计和参数的输入，设计时只输入最小簧丝直径和变径材料长度，通过设计Matlab程序自动计算相应的螺旋弹簧参数.变簧丝直径的螺旋弹簧同样可以设计成圆柱形和圆锥形等形状，并自由组合成不同形状的弹簧段.通过定义每一段弹簧的节距或螺旋升角，精确计算弹簧压缩过程中有效工作圈的变化，得到弹簧在不同高度时的载荷和刚度.因此，想要解析变参数螺旋弹簧的刚度特性，首先要从研究普通定常参数螺旋弹簧入手[2].

2.1 普通圆柱螺旋弹簧刚度分析

普通定常参数圆柱螺旋弹簧的几何形状是呈圆柱螺旋形.以螺旋弹簧材料中心线形成的螺旋线的基本参数如图2所示，D为弹簧中径，α为弹簧螺旋角，l为弹簧有效圈材料展开长度，θ为坐标系极角，n为弹簧有效圈数.

根据D、α和l这3个基本参数，可以确定如下几何参数：

1)弹簧节距

t=πDtanα，

(1)

2)弹簧有效圈数

(2)

3)螺旋高度

H0=nt=lsinα，

(3)

4)螺旋线的曲率半径

.

(4)

圆柱螺旋弹簧在轴向压缩载荷F和扭矩T作用下，受力情况如图3所示，其变形量为

(5)

式中：Ip为材料的极惯性矩；I为材料的惯性矩；G为材料切变模量；E为材料弹性模量；A=πd2/4.

由于螺旋弹簧在车辆悬架应用中只承受轴线方向的外载荷F，因此变形在弹簧两端所引起的力矩较小，可以忽略不计.在实际应用情况中，螺旋角α<9°，此时取cosα≈1,sinα≈0.截面材料

图2 圆柱螺旋弹簧 图3 螺旋弹簧受力示意图

形状为圆柱体时，式(5)可化简为

f=8FD3n/(Gd4).

(6)

以簧丝直径d=2.5 mm，弹簧中径D=9 mm的单圈弹簧为例，当其它参数不变时，单独改变簧丝直径d或弹簧中径D,根据式(6)计算螺旋弹簧的刚度结果如图4所示.由图4可知，簧丝直径d和弹簧中径D的改变对弹簧刚度影响很明显.

图4 螺旋弹簧刚度

在变参数螺旋弹簧中，单圈的刚度相差越大，弹簧的非线性刚度特性就会越明显.若想通过改变簧丝直径或弹簧中径达到理想刚度特性，螺旋弹簧的材料形状变化率必然会很大，无法满足制造和车辆装配的要求.因此通过对簧丝直径d、中径D和节距t三参数同时改变，不但可以使“三变”螺旋弹簧可以实现理想刚度特性，而且也可以明显减小材料的变化率.同时，对三个参数同时进行优化匹配，可以保证在得到理想刚度特性的情况下控制弹簧的最大应力小于许用应力，使“三变”螺旋弹簧不仅限于理论计算.

2.2 变参数螺旋弹簧数学模型建立

由于结构限制，螺旋弹簧的非线性刚度特性是通过改变有效圈数实现的，而变参数螺旋弹簧单圈刚度和节距均不相同，在载荷不断增大的过程中，螺旋弹簧簧圈之间顺序压并，有效圈数逐渐减少刚度增大.借鉴离散化思想对变参数螺旋弹簧刚度特性进行解析计算，将整根弹簧离散为有限个单元，在每个单元中，簧丝直径、中径这些变化量可以近似视为不变量.通过编制计算程序求出一定载荷下各个单元的变形量，再将其合成求得螺旋弹簧总的变形量.

下面建立螺旋弹簧参数数学模型.根据车体轮舱的安装空间得到螺旋弹簧自由高度H0、弹簧簧丝直径和中径，如图5所示.

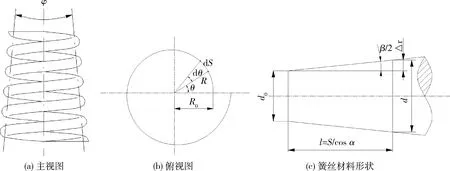
图5 变参数螺旋弹簧

计算变参数螺旋弹簧的压并过程，需要计算出第k圈的压并载荷Fk和此时弹簧总体位移fk.因此，首先分析弹簧簧丝直径d、簧圈半径R及簧丝材料顶视长度S与极角θ之间的关系，如式(7)～式(9)所示.

(7)

(8)

(9)

对变参数螺旋弹簧进行离散化解析，求出螺旋弹簧在受轴线方向载荷时的轴向变形量.当载荷F沿螺旋线方向作用时，只考虑簧丝截面中心线的扭矩作用.在扭矩T的作用下，螺旋弹簧的轴向变形为

(10)

式中：簧丝转角dφ=TdS/(GIp)，T=FR，dS=Rdθ，Ip=πd4/32.

将式(7)、式(8)代入式(10)，积分上限取θ、下限取0，得到螺旋弹簧位移关系式为

(11)

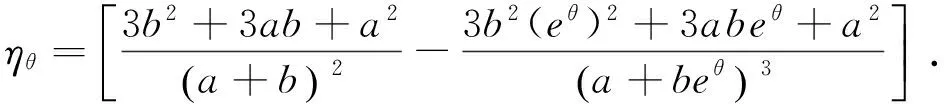
根据式(11)能够推导出螺旋弹簧每一段微元体的刚度系数.将上述数学模型编制成Matlab程序.然后运用Matlab程序计算每个微元段的位移-载荷关系，最后将所有微元段的位移-载荷关系串联合成螺旋弹簧整体的刚度特性.根据本节推导的数学模型可以明显看出，变参数螺旋弹簧的单圈刚度是递增的，在载荷不断增加的过程中弹簧簧圈顺序压并，从而达到减少螺旋弹簧有效圈数、增大螺旋弹簧刚度的目的.

2.3 某车型变参数螺旋弹簧参数设计

某车型中应用的油气弹簧刚度特性曲线如图6中实线所示.将车辆悬架系统的装配尺寸作为边界条件，得到变参数螺旋弹簧的最小中径和最小簧丝直径.若考虑车辆在非越野路面行驶时要达到的舒适性，那么螺旋弹簧从自由高度到静载位置的刚度应该是线性的，即从自由高度压缩至车辆静载位置时弹簧簧圈不发生压并.

为了避免计算过于复杂，设计时只取油气弹簧空载、满载和最大动行程的位移-载荷数值点.将螺旋弹簧线性段的刚度、三个位移-载荷的数值点和悬架弹簧行程输入编制的Matlab程序中，计算出变参数螺旋弹簧的参数.以最大应力为优化目标对变参数螺旋弹簧参数进行优化，得到如图6中虚线所示的变参数螺旋弹簧解析刚度特性曲线.

将Matlab优化后的参数输入三维建模软件中，绘制变参数弹簧结构形状如图7所示.弹簧有效圈数n=6，最小弹簧中径D0=83 mm；最大弹簧中径Dmax=88 mm；最小簧丝直径d0=32 mm；最大簧丝直径dmax=43 mm.

图6 变参数螺旋弹簧与油气弹簧的刚度特性对比

图7 采用计算程序设计的悬架变参数弹簧

3 结束语

将离散化思想与弹簧基本设计理论相结合，提出一种对变参数螺旋弹簧的解析计算方法，并给出基本运算思路.以某型车辆悬架系统为基础，对变参数螺旋弹簧进行了解析计算，得到变参数螺旋弹簧的主要参数，并对其刚度特性进行解析计算，结果表明变参数螺旋弹簧也可以具有良好的非线性刚度特性，能够替代油气弹簧中的弹性元件.

[1] 周良生. 变参数压缩螺旋弹簧的性能评述[J]. 汽车工程. 2004，26(6)：696-701.

[2] 张英会. 弹簧手册[M]. 北京：机械工业出版社，2001.

[3] 王跃辉. 一种基于螺旋角的螺旋弹簧全新算法[C].//中国汽车工程学会年会论文集，2015.

Research on Stiffness Characteristics of Helical Springwith Variable Parameters

NIE Wei， LEI Qiang-shun, CHEN Yi-jie, GAO Xiao-dong, GUI Peng

(China North Vehicle Research Institute, Beijing 100072, China)

The mathematical model of variable parameter helical spring compression process is established based on discrete concept and basic theory of helical spring. Based on the stiffness characteristics of hydro-pneumatic spring and taking the actual vehicle assembly dimensions as the constraint, the structure parameters of the variable parameter helical spring were calculated by Matlab program. By comparing the stiffness characteristic curves, the results show that the stiffness of variable parameter spring can be close to the stiffness of hydro-pneumatic spring.

helical spring; variable parameters; stiffness characteristics

1009-4687(2017)01-0021-04

2016-11-21； 修回稿日期：2017-01-09.

聂维(1989-)，男，硕士研究生，研究方向为车辆悬挂技术.

U463.33+4.01

A