基于能量比法识别波头的AT牵引网故障行波测距研究
牛琼,李东辉,李诗涵
(1.大连交通大学 电气信息学院,辽宁 大连 116028; 2.杭州迪普科技有限公司,北京 100085)*
基于能量比法识别波头的AT牵引网故障行波测距研究
牛琼1,李东辉1,李诗涵2
(1.大连交通大学 电气信息学院,辽宁 大连 116028; 2.杭州迪普科技有限公司,北京 100085)*
针对AT供电方式牵引网的故障定位问题,提出了一种新的基于能量比法的故障测距算法,目标在于提高故障测距精度,缩短定位时间,满足高速铁路列车的应用需求.利用MATLAB软件建立了AT供电方式下的某牵引网结构的仿真模型,并对故障测距算法进行了仿真验证.仿真结果表明:与在变电所调研的故障测距结果相比,误差小于变电所中故障测录仪获得的故障测距误差,定位时间较短,故障测距精度提高,这为后续相关研究及探索奠定了重要基础.
AT供电;故障测距;能量比法; 算法
0 引言
牵引供电系统[1]是电气化铁路的基础,由于高速电气化铁路行车密度大、运行速度高,AT(Auto Transformer)供电方式[2- 3]以其更高的可靠性、更长的供电区段、更大的供电功率成为了我国高速铁路现阶段的主流供电方式.
目前,针对AT供电方式多为利用牵引网各点电流比值[4]来进行故障测距,容易受到线路结构、牵引网的运行方式及故障类型等因素的影响,导致测距精度不高.而行波法具有较好的精度和稳定性[5- 7],当前求取时延应用比较广泛的是小波分析[8]和相关分析法:小波分析法本质是利用小波变换的奇异性检测原理来检测出信号突变点,而相关分析法则是通过判断波头相关性得出行波波头时延.相较这两种方法,能量比法对有更复杂噪声扰动或者传播线路更复杂的信号在获取时延[9]上更加简单,不仅算法的稳定性比较高,而且计算时参数的选择更方便,实际应用价值更高.在此基础上,本文重点研究AT供电方式牵引网中行波法的应用,并在现有测距方法的基础上提出利用能量比法处理故障行波,计算波头时延,实现较精确的故障定位.
1 能量比法
能量比法[10]以信号能量在一个时间窗内的有效值差异特征为基础,将信号突变点凸显出来,使有用信号达到测量点的时候,更加清晰明了[11].
能量比法的计算是一个时间窗逐点移动的过程,首先选择一定宽度的时间窗,然后从记录的起点一直移动到记录的终点,这样某个信号能量比法的计算就完成了.能量比法的基本公式如下:
式中:P为时窗内后、前能量比,x(t)为时间窗内的相对能量,对应为电压正向行波,T1为时窗起点,T0为时窗中点,T2为时窗终点.
由上式可以看出,影响定位准确性的一个重要因素就是选择的时间窗宽的大小,该大小的选择会改变模极大值点的位置,从而影响故障定位的准确性[9].时间窗宽选小时突变点位置更精确,但会导致时间窗前后信号差异不够明显,无法凸显突变点,有可能会不能准确显示突变点位置;而较大的时间窗宽虽然会得到较大的模极大值,凸显突变点的位置,但波形不够尖锐,无法得到精确的时间点.
2 AT供电方式牵引网的建模
2.1 牵引网基本结构
本文主要讨论哈大高铁[12]某两个牵引变电所之间的牵引网部分,牵引网线路结构与各线参
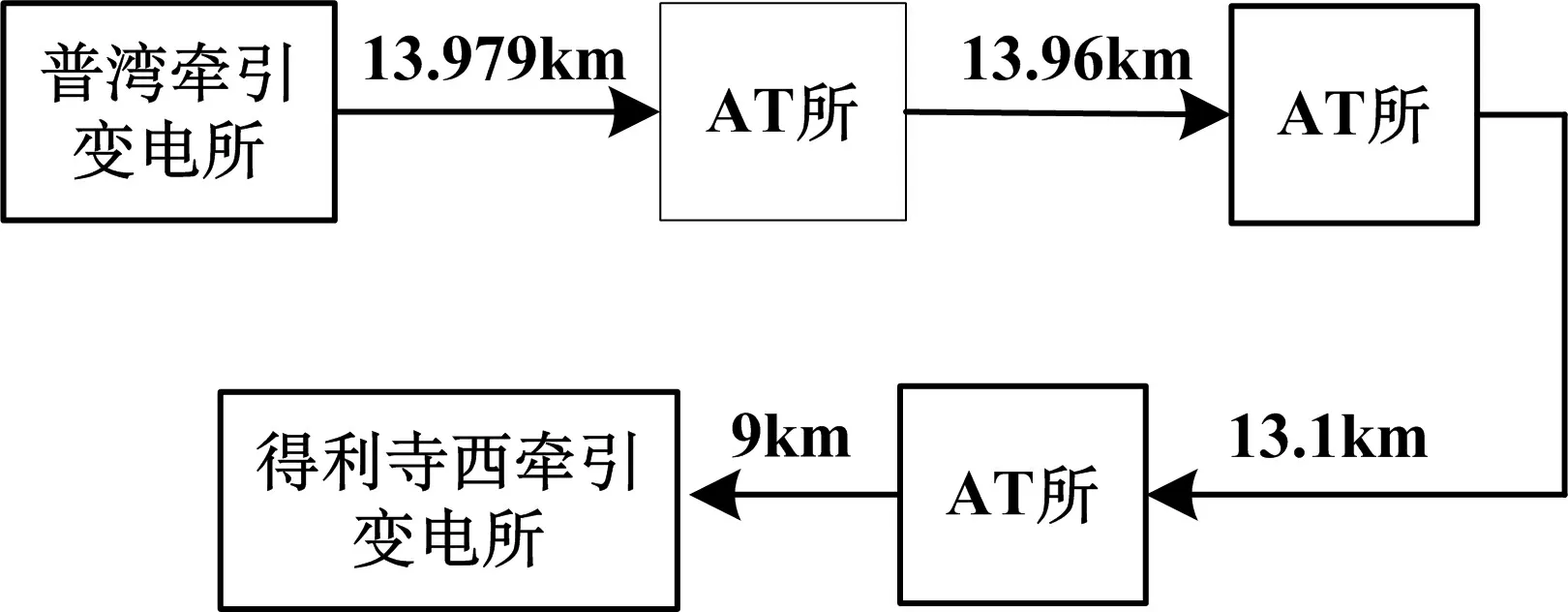
图1 A-B变电所间的牵引网简单分布图
数可以通过牵引网及数值计算得到.图1给出两变电所之间的牵引网简单分布图.
2.2 牵引变电所接触网建模
基于MATLAB仿真平台,在阻抗和电容矩阵计算的基础上,搭建的两变电所之间牵引网故障测距模型分别由AT所模块、牵引变电所模块、线路模块、故障模块、机车模块、测量模块等组成[13].由于以上模块在MATLAB仿真平台中没有直接给出,需要根据牵引网的实际情况,利用Simulink中的电力元件对元件进行组合、连接及封装,然后连接封装的模块建立完整的AT供电方式牵引网故障测距仿真模型,结合调研的牵引网的现场线路参数情况对各个模块进行准确的设置.牵引变压器及AT变压器具体参数设置如表1和2所示.

表1 牵引变压器参数

表2 AT变压器参数
3 牵引供电系统仿真与结果分析
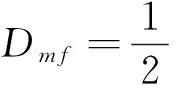
3.1 行波提取
行波可以分为正向行波和反向行波,假设行波由故障点指向线路两侧的传播方向是正向,那么由线路两侧指向故障点的方向即为反方向,从故障电压、电流波形中提取出正确的正反向行波对行波故障定位意义重大.运行MATLAB对短路故障仿真之后,在测量显示模块中获得的故障电流和电压数据会被保存到Workspace中,且以变量形式储存.把T、R、F看作三相,然后根据故障发生时T、R、F的电压和电流数据来获取电压的正反向行波,具体提取方法如下:
(1)提取T、R、F中的电流、电压暂态故障分量.用故障发生时刻至之后某段时间内的T、R、F的电压、电流值减去故障前相对应的某段时间内的T、R、F的电压、电流,就能得到T、R、F的电压、电流的暂态量uT、uR、uF和iT、iR、iF;
(2)为获取故障电压、电流的模量值um和im,将T、R、F的电压、电流的暂态量uT、uR、uF和iT、iR、iF进行模量变换.
(3)uf1、ur1为获取电压1模的正向和反向行波,其公式如下[14]:
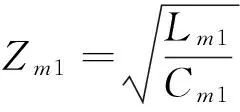
3.2 能量比法的应用
得到电压正向行波后,利用能量比法对获得的电流和电压信号进行操作,可以把信号边缘扩大,获得故障时延,从而实现牵引网的准确故障定位.根据前文分析,选择的时间窗的大小会极大的影响能量比函数使用的有效性,如果时间窗选择的比较符合要求,那么会得到比较准确的故障信息,从而实现精确定位[15].
经实验验证,时间窗宽为30μs时其模极大值点比较方便读出,因此本文选择在此时间窗宽下实现能量比函数法.
由能量比曲线可以得到首波头位置、第二个波头的位置,从而得到两个波头的时间间隔.而且,能量比函数曲线可以快速判断出第二个波头的极性和初始波头极性的关系.
3.3 不同情况下的行波测距
AT供电方式牵引网有多种短路故障,其中接触网—正馈线(T-F)短路、正馈线—钢轨(F-R)短路、接触网—钢轨(T-R)短路是三种主要的形式,本文主要对T-R短路故障进行了仿真,采样时间取0.000 01s,仿真时间取0.1s,故障发生时刻取0.04s.
3.3.1 不同故障点位置下的行波测距
故障点至测量安装点的距离分别为:近端故障5.92、9.79km,中端故障18.42km,远端故障30.08、37.8km,以距离安装处5.02km处发生T-R短路故障为例.
故障模块设置在距离牵引变电所5.02km处,过渡电阻取0.001Ω,相位角取0°,通过仿真得到该故障位置时的波形图.
仿真得到故障电流、电压波形,可以看出在t=0.04s处电流明显增大,电压稍微减小,即在0.04s时发生了短路故障.不能把每一种情况下的故障电压、电流波形都显示出来,但通过仿真可以看出其变化符合一般规律:随着故障点距离电源越来越远,故障点时电压减小的幅度越来越不明显,而电流的峰值也越来越小.
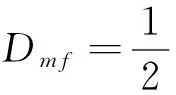
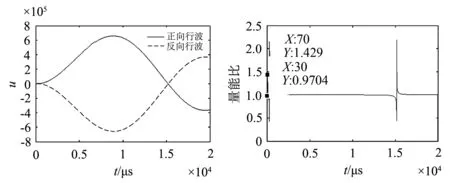
(a) (b)
图2 故障位置在5.02 km的电压正、 反向行波和能量比函数曲线
通过改变短路点的位置并运行模型及程序可以获取短路点在其他位置的故障电流、电压图形,正、反向电压波形以及能量比函数曲线.
通过5.02、9.79、18.42、30.08、33.8 km五组不同故障位置时的能量比函数曲线,使用matlab中Data Cursor工具对模极大值点进行准确标注,然后将获取的时间间隔数值代入行波故障测距的计算公式,可得到故障距离及误差如表3所示.
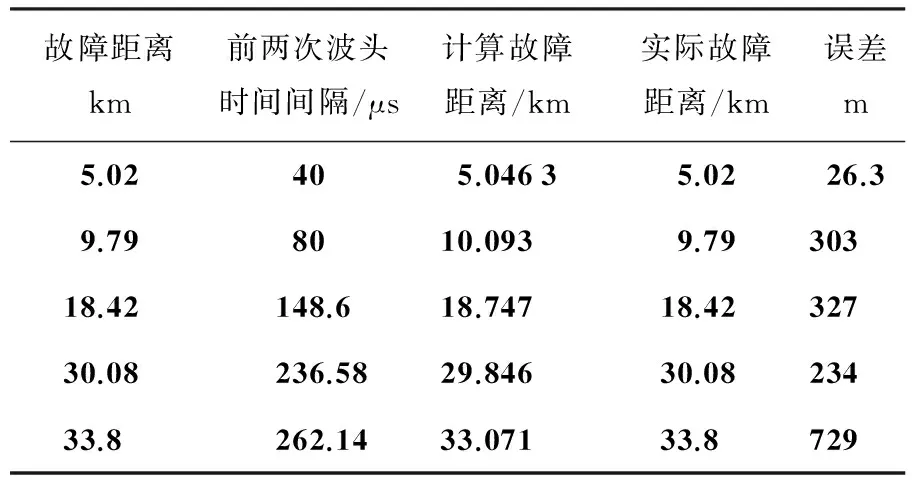
表3 不同故障点位置的定位结果
由表3可以看出,随着故障点距离测量点越远,故障测距的误差越大,这符合一般规律,且其误差大小低于在变电所调研时故障测录仪测得的误差,满足本论文的测距要求;通过对比近端故障以及远端故障下的测距误差,可以看出距离AT所较近的点的误差相对于距离较远的点也略大,这是由于AT所对行波测距造成的影响导致的.
3.3.2 不同过渡电阻下的行波测距
使用三组数据来分析故障点在5.02 km时,在0.001、10、100 Ω不同过渡电阻条件下的行波故障定位仿真,根据能量比法得到故障测距的结果,从而分析过渡电阻的大小对行波故障测距的影响.以过渡电阻为0.001 Ω为例.
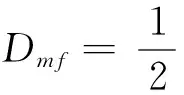
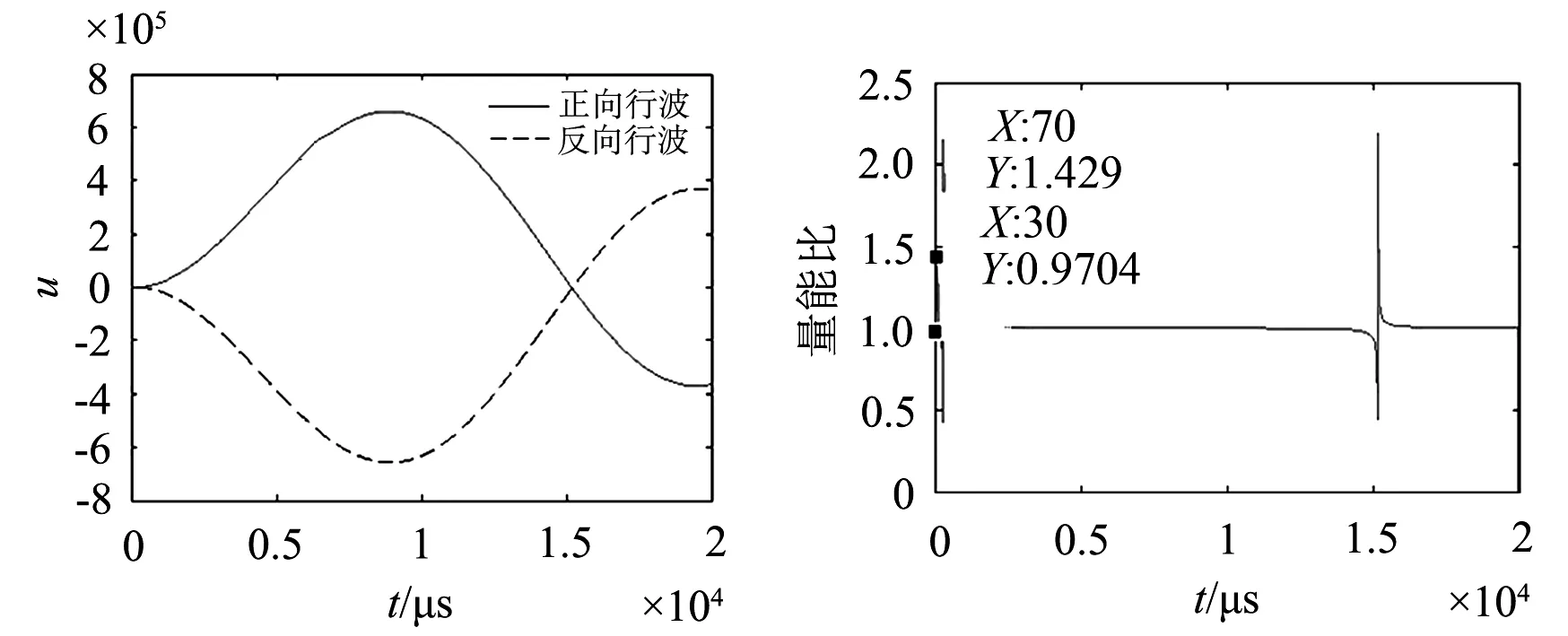
(a) (b)
图3 过渡电阻是0.001 Ω的电压正、 反向行波和能量比函数曲线
通过0.001、10、100 Ω三组故障波形发现,取的过渡电阻的数值依次增大,电压正、反向行波的的最大值呈显著减小趋势,从能量比函数曲线中可以看到,对于获取准确的模极大值时延时不会造成任何影响,即在AT供电方式牵引网中基于能量比法的行波故障测距不受故障过渡电阻的影响.不同过渡电阻的故障点位和误差如表4所示.
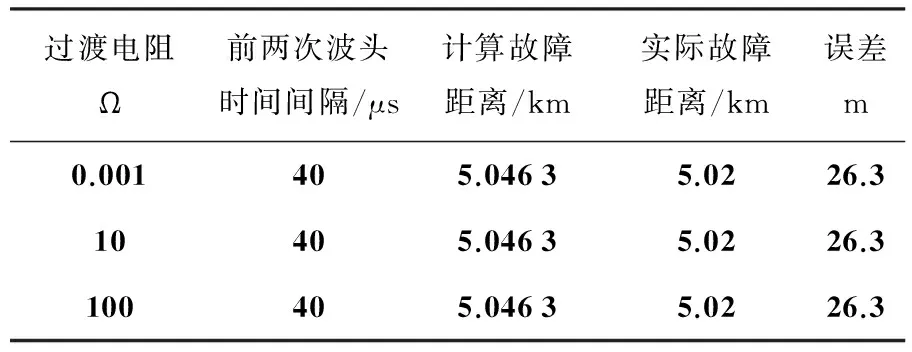
表4 不同过渡电阻的定位结果
3.3.3 不同相位角时的行波测距
取不同的故障相位角时获得的故障电流和电压波形不同,所以对此做了仿真分析.以故障点位置为5.02 km,过渡电阻为0.001 Ω的电路模型为例,对故障相位角分别取 0°、45°,135°三个不同数值时进行仿真.以相位角为45°为例.
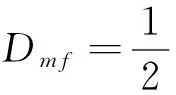
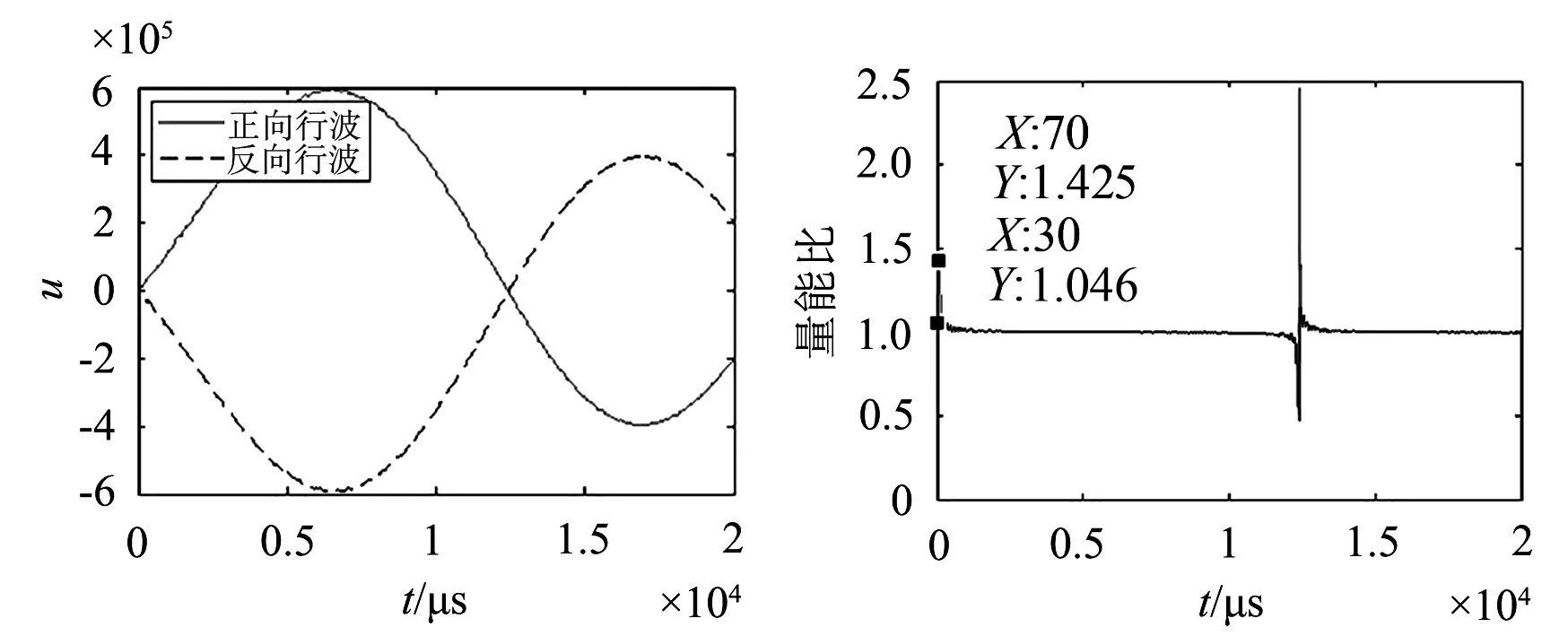
(a) (b)
图4 相位角为45°的电压正、反向行波和能量比曲线
通过对比三组故障相位角(0°、45°、135°)的电压正、反向波形可得到,虽然波形上有些不同,但对于之后模极大值时刻的判定,依然没有影响.不同故障相位角时故障定位和误差如表5所示.
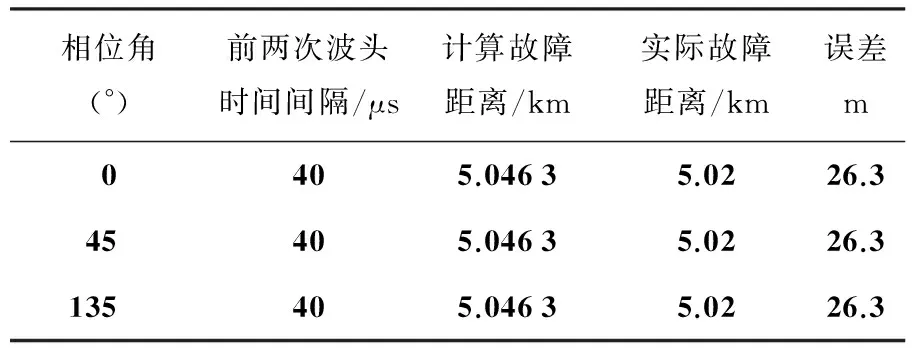
表5 不同故障相位角的测距结果
4 误差分析
由测距结果可以看出,故障相位角及故障点过渡电阻对测距结果没有影响,而对于不同故障点位置,通过对比近端以及远端故障下测距误差,可以看出故障位置距离AT所越远,测距误差也会越大.除了距离越长过渡电阻和电压损耗越大等原因,下面简单分析造成上述情况的可能因素.
(1)吊弦的影响
接触线通过吊弦悬挂在承力索上,吊弦是接触网的重要组成部分.
行波在传播过程中遇到吊弦,折射和反射都会受到影响,在金属中的损耗会导致行波到达测量端已被削弱甚至根本无法到达测量端.
(2)波速的影响
本文中所用的行波波速为:
式中:c=3×108m/s为光速;μ是导线周围介质导磁系数;ε是导线周围介质介电系数.导线的形状、介电系数、自身材料以及导线四周的环境,都会影响线路的行波波速.
所以,吊弦干扰和行波波速选取是影响远端测距误差的重要因素.
5 结论
与在变电所调研的故障测距结果相比,误差小于变电所中故障测录仪获得的故障测距误差,满足了测距要求.但鉴于建模、行波提取、使用能量比法时会有误差存在,以及误差分析中提到的影响因素,还有更进一步优化测距结果的可能,需要进行更深入的研究和验证.
[1]谭秀炳.交流电气化铁道牵引供电系统[M].成都:西南交通大学出版社,2009.
[2]邢晓乾. 三种牵引供电方式的电气特性比较[J]. 电力学报,2013(1):35- 39.
[3]林依姜.牵引网故障测距[J]. 海峡科学,2011(11):20- 21,28.
[4]高仕斌,王伟,陈小川,等.AT供电牵引网新型微机故障测距原理与应用[J]. 铁道学报,1993(4):19- 27.
[5]段晶晶.基于行波原理的直供方式牵引网故障测距技术[D].山东:山东理工大学,2010.
[6]陈强强.AT供电方式接触网行波故障测距的研究[D].南昌:华东交通大学,2012.
[7]杨金岳.AT供电方式牵引网行波故障测距研究[D].南昌:华东交通大学,2013.
[8]周建辉,康劲松,徐国卿. 基于复小波分析的牵引网故障测距算法[J]. 同济大学学报(自然科学版),2010(12):1818- 1821,1860.
[9]韩志锟.小相角故障行波测距方法研究[M].电工电气,2013(4):28- 32.
[10]韩志锟,饶曙勇,姜玉山,等. 基于能量比法的输电线路行波故障测距[D]. 电网技术,2011(3):216- 220.
[11]卢毅,韩志锟,陈瑜.基于能量比预处理的FFT窄带滤波方法[J].东南大学学报(自然科学版),2010(5):948- 951.
[12]朱飞雄,张伟. 哈大线牵引供电系统及其特点[J]. 电气化铁道,1999(1):39- 40.
[13]张茜.基于BP的全并联AT牵引网故障测距方法研究[D].成都:西南交通大学,2011.
[14]程云强.基于接触网的双端行波故障测距的应用[J].江西科学,2012,30(2):207- 210.
[15]夏远洋.串补线路的行波故障测距研究[D].西安:西安科技大学,2013.
Study of Contact System Fault Location based on Energy Ratio Method
NIU Qiong1,LI Donghui1,LI Shihan2
(1.School of Electrical and Information Engineering,Dalian Jiaotong University,Dalian 116028,China; 2.HangZhou Dipu Technology Co.,Ltd,Beijing 100085,China)
Aiming at fault location problem of the traction electric network in AT power supply mode, a new fault location algorithm of the traction network in AT power supply based on the energy ratio method was put forward, and aimed to improve the precision of fault location and shorten the fault positioning time so as to meet the application demand of the high-speed locomotives. The simulation model of a traction electric network structure in AT power supply mode is established using MATLAB software, and the fault location algorithm was simulated and verified. Simulation result show that the fault location error is less than the measured fault location error in substation, and the positioning time is shorter, and the accuracy of fault location is improved.
AT power supply mode;fault location;energy ratio method;algorithm
1673- 9590(2017)02- 0099- 05
2016- 01- 06
牛琼(1991-),女,硕士研究生; 李东辉(1970-),男,副教授,博士,主要从事铁路电气新技术、电磁兼容性的研究
E-mail:695940191@qq.com.
A

