瞬态风场下带风屏障的高架桥上高速列车气动特性

吴超,杜礼明

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

瞬态风场下带风屏障的高架桥上高速列车气动特性

吴超,杜礼明

(大连交通大学 交通运输工程学院，辽宁 大连 116028)*

通过数值方法研究了中国帽型瞬态风中高速列车在带风屏障的高架桥上运行时的气动性能，并与恒定横风场下的情况进行了对比分析.结果表明，恒定侧风下高速列车头车周围的流场结构最为复杂，气动载荷变化最显著，而瞬态风作用下高速列车气动性能表现出一定时滞性，列车时速为300 km/h时，风速从13.8 m/s递增到23.46 m/s再递减至13.8 m/s过程中，列车所受到的气动力及气动力矩均发生显著波动，这与稳定横风下列车受到的恒定侧向力明显不同.当列车以时速200～400 km/h运行时，车速每增加50 km/h，列车运行的最大阻力增长9%～10%，其他气动力也随车速稳步增长，气动力矩的增大幅度则随车速的增长有显著加大趋势.

自然瞬态风；高速列车；高架桥声屏障；气动特性；数值分析

0 引言

强横风作用是影响高速列车侧风稳定性的主要因素之一，使列车发生脱轨或倾覆的危险性增大.近年来，各国学者对高速列车风致安全性问题开展了大量研究，以提出应对大风的策略.罗建斌等[1]采用数值模拟方法探讨横风中高架桥声屏障高度对高速列车气动特性的影响.然而，自然风具有明显的随机性，稳态方法无法预测其不确定性特征.文献[2-3] 建立了阵风环境下车辆运行可靠性的分析方法.但理想阵风是对自然风的一种抽象形式，只考虑自然风速的最大幅值和持续时间，不能预测出自然风的脉动特性.文献[4]基于COOPER理论和谐波叠加法计算了随高速列车移动的点的脉动风速，并推导出非定常气动载荷的概率分布特性.但现阶段该统计特性很难与计算流体动力学软件实现对接，只能提供理论上的统计数据，不能在三维模型上实现自然风动态的变化过程.

本文采用欧洲通用标准(TSI)提出的“Chinese hat”动态风场模型[5]来近似模拟动态风场，将动态风速历程用双三角函数描述，建立有风屏障的双线高架桥上高速列车空气动力学的仿真模型，并通过Fluent软件的UDF功能模拟自然瞬态风，分析列车表面压力以及气动力，研究自然瞬态风对高速列车气动性能的影响，并与恒定风场下的情况进行对比，为高速列车在带风屏障的高架桥上安全运行提供参考.

1 数值模型与计算方法

1.1 仿真模型及气动力定义

列车是复杂的细长结构，若对整列列车的流场进行数值模拟，不仅计算量大、对计算机的要求高.因此，经简化后本文采用的双线高架桥CAD模型如图1所示，参考国内某CRH型高速动车组的几何外形，采用头车+中间车+尾车的三辆车编组的简化模型进行仿真.

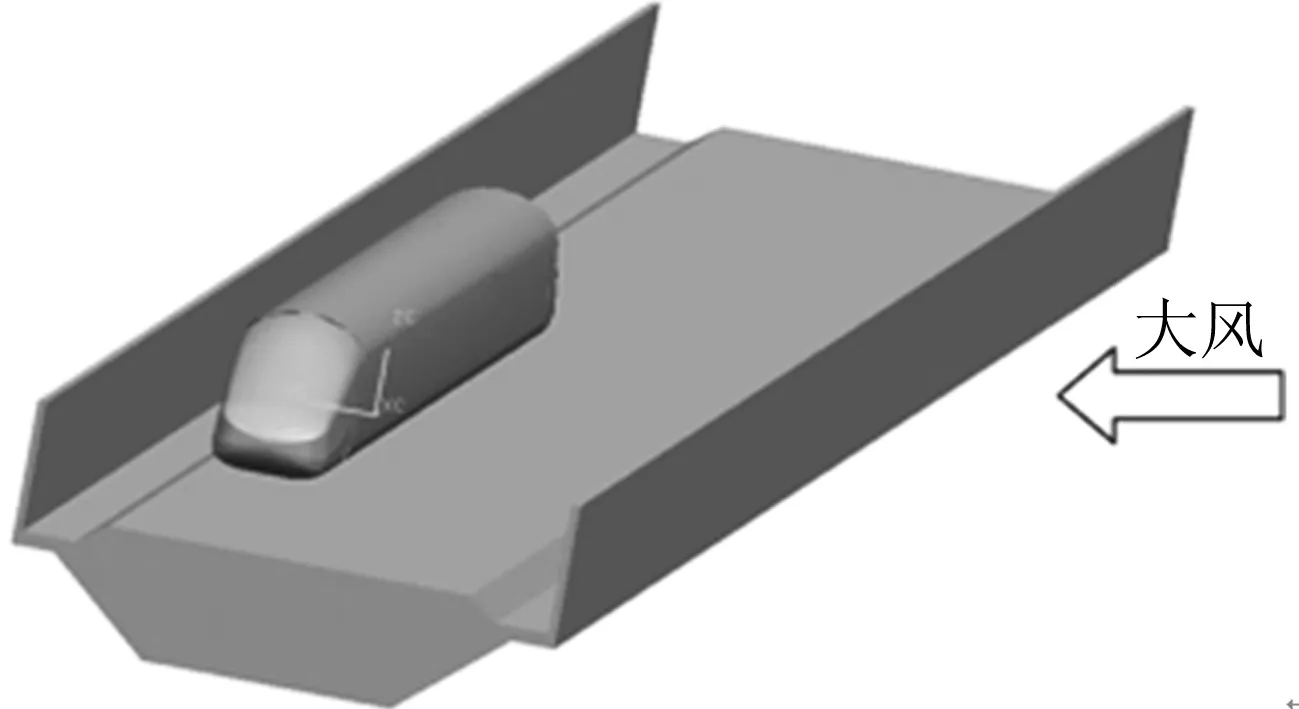
图1 双线高架桥及高速列车CAD模型

在瞬态风环境中,流场对列车的作用一般等效为气动作用力和力矩.为便于计算,本文在高速列车空气动力学模型中建立坐标系,如图2所示.分别为阻力Fx、侧力Fy、升力Fz.侧滚力矩Mx、点头力矩My、摇头力矩Mz.

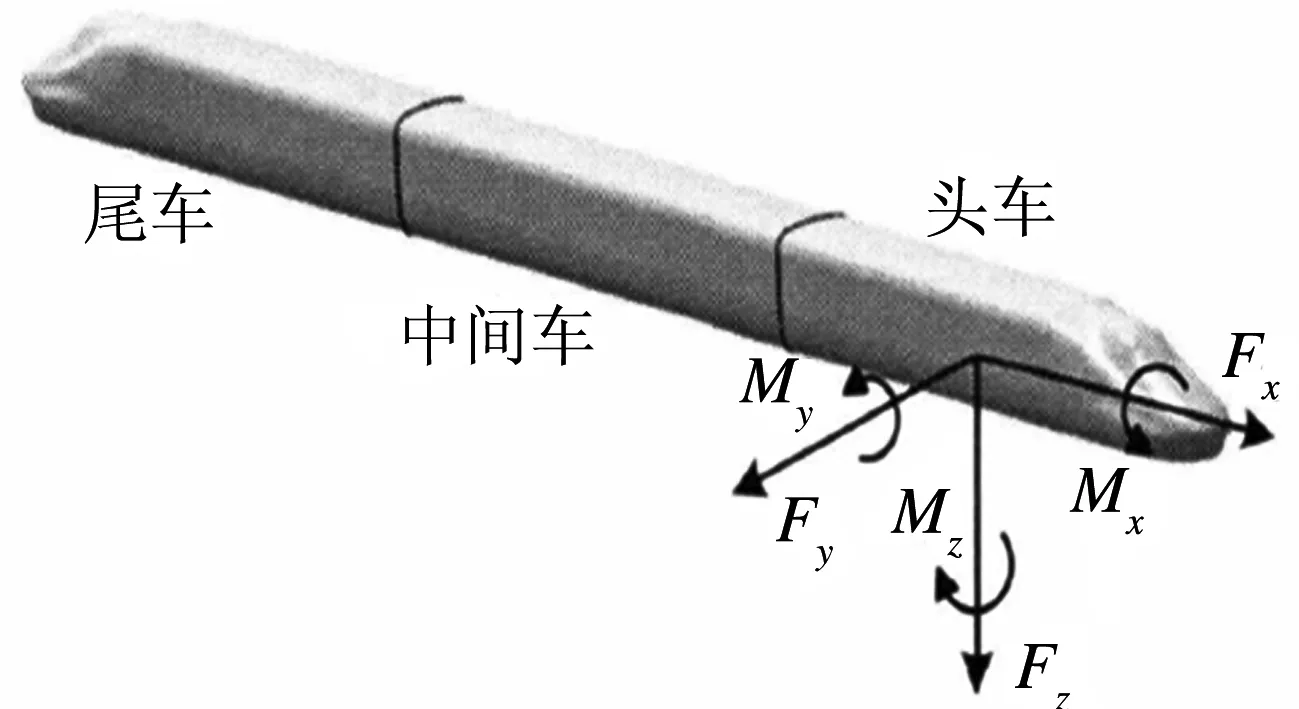
图2 气动力与气动力矩定义示意图

1.2 计算区域及网格划分

在不影响列车附近流体的流动情况下，为减少计算量，模拟时列车运行的外流场只能取有限的空间，计算域如图3所示.

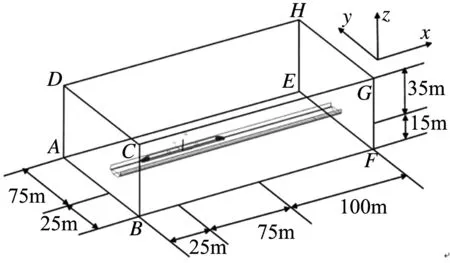
图3 计算域及坐标系

为提高计算效率，划分网格后需要对计算域网格进行优化.通过错略网格的试算，最终确定的四面体网格总数约为3×106，如图4所示.

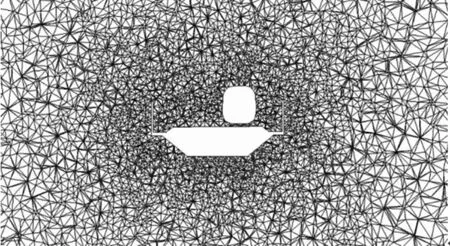
图4 计算网格

1.3 自然瞬态风模型

现场观测表明，自然风速总是围绕某一稳定值波动，其稳定值即平均风速，而围绕平均值波动的部分即脉动风速，如图5所示[5].鉴于以上分析，在考虑计算效率前提下，既不失自然风脉动规律性，同时考虑自然风的极端变化情况，将模型简化为图6所示.

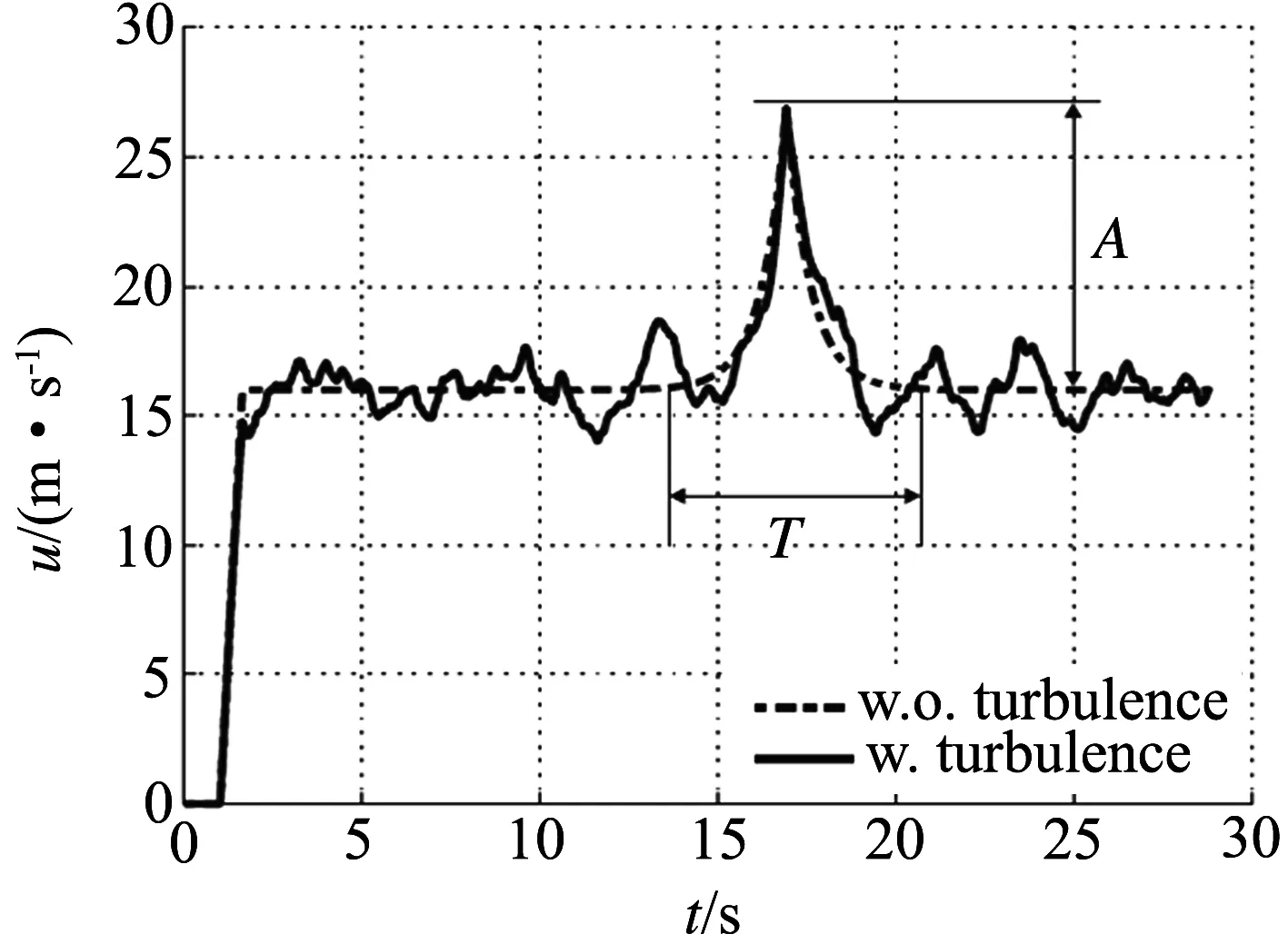
图5 自然风观测记录

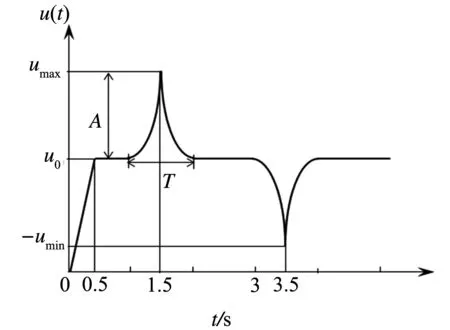
图6 简化后自然风模型

其中，动态自然风风速由稳定风速和脉动风速叠加

(1)

式中，U为自然风风速，u0为稳定风风速，uG为脉动风速，T为脉动风持续时间，0～4s为不同风速变化规律时间区段，umax为最大风速，其与稳定风速u0的比值A为动态风速脉动幅值比.根据经验数据[6]，在进行数值计算过程中，取T=1s, A=1.7.

由图5可知，“Chinesehat”双三角函数自然风模型描述的动态风速变化可由分段函数表示

1.4 模拟方法及边界设置

基于Fluent软件提供的用户自定义函数接口UDF，编写自然瞬态风函数程序，并将该程序动态加载到Fluent上.由于自然瞬态风与列车风的最大合成速度马赫数小于0.3，因此列车周围的气体流动可按三维、黏性、不可压缩湍流流动处理，湍流模型选用两方程模型，压力与速度耦合处理方式选用SIMPLEC算法,数值离散采用二阶迎风格式.

参照图2所示的计算域，边界条件设置如下：

(1)计算域流动入口：列车前进方向入口ABCD施加均匀风场，其大小为列车运行速度，本文中取列车的运行速度为300 km/h，方向与列车运行方向相反；横风速度入口BCFG参考国际标准风力等级表中6级风速上限值，即13.8 m/s;

(2)计算域流动出口：使用压力出口边界条件，压力设置成一个标准大气压;

(3)列车表面：列车表面设置成有一定粗糙度的固定壁面边界，考虑列车表面边界层效应的影响;

(4)地面：为了消除地面效应的影响，更加准确地模拟列车运动情况，地面采用滑移壁面边界条件.

1.5 计算方法适用性验证

为验证本文数值模拟方法适用性及准确性，参照文献[7]中在中国空气动力研究与发展中心8m×6m风洞进行的缩尺模型试验所得到的数据，与缩尺模型的数值模拟结果进行了对比分析，对比数据如表1所示.

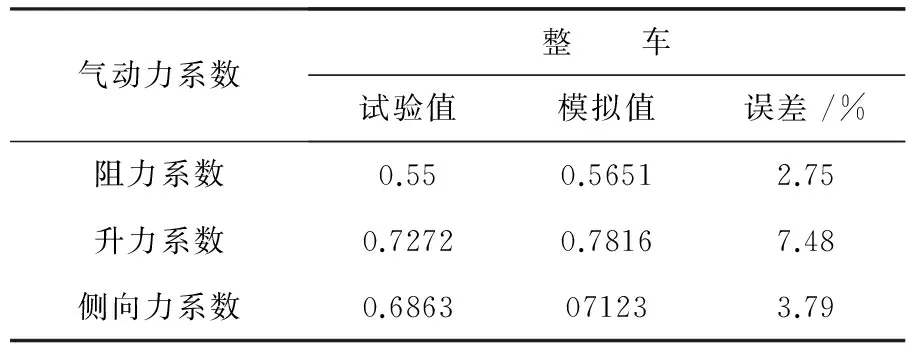
表1 缩尺模型试验与相应数值模拟的结果对比

由表1可知，数值模拟与其缩尺模型试验的气动力系数误差在10%左右，在工程允许的误差范围内.

2 结果与分析

2.1 横风作用下列车的气动特性

为了对比分析瞬态风对高速列车的影响，首先对恒定风速下的高速列车头车、中间车、尾车的气动特性进行分析.取列车运行速度为300km/h，横风风速13.8 m/s，风向角90°，即风垂直吹向列车侧面，图7为头车迎风侧和背风侧表面气动压力的对比.

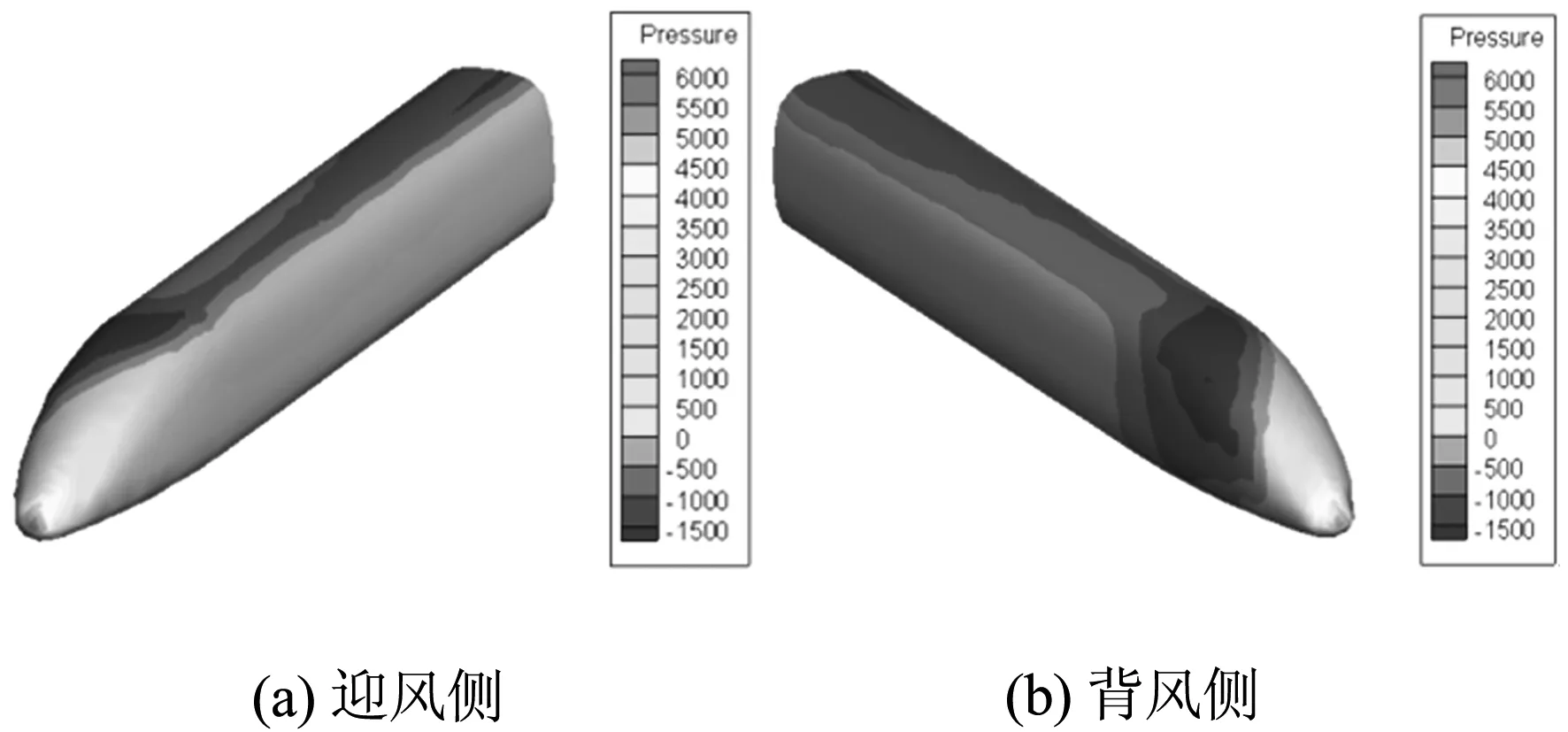
图7 头车表面压力云图

如图7所示，在横风环境下头车迎风侧为正压，背风侧为负压.最大正压出现在迎风一侧的鼻尖处.这是由于横风的影响，虽然有风屏障的阻挡，但仍有部分气流吹向列车一侧，从而最大压力偏向迎风侧鼻尖处.

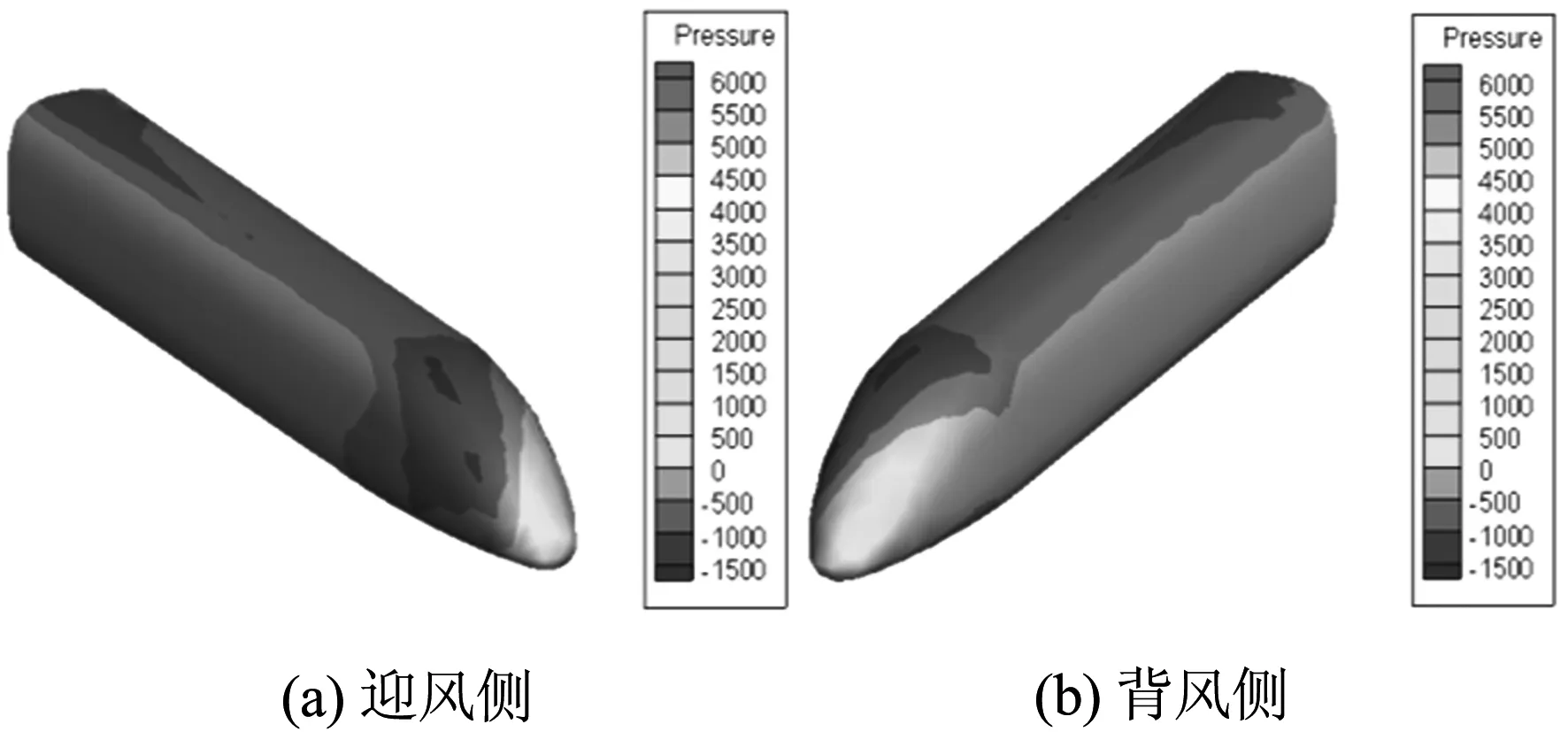
图8 尾车表面压力云图

图8为尾车表面的气动压力分布，在列车车尾的迎风侧出现了负压区，而背风侧出现大面积的正压区，导致列车车尾所受到横向力的作用方向正好与头车相反.

在列车长度方向上取三个截面，得到列车在运行时头车、中间车、尾车横截面上的压力云图和速度流线分布如图9所示.

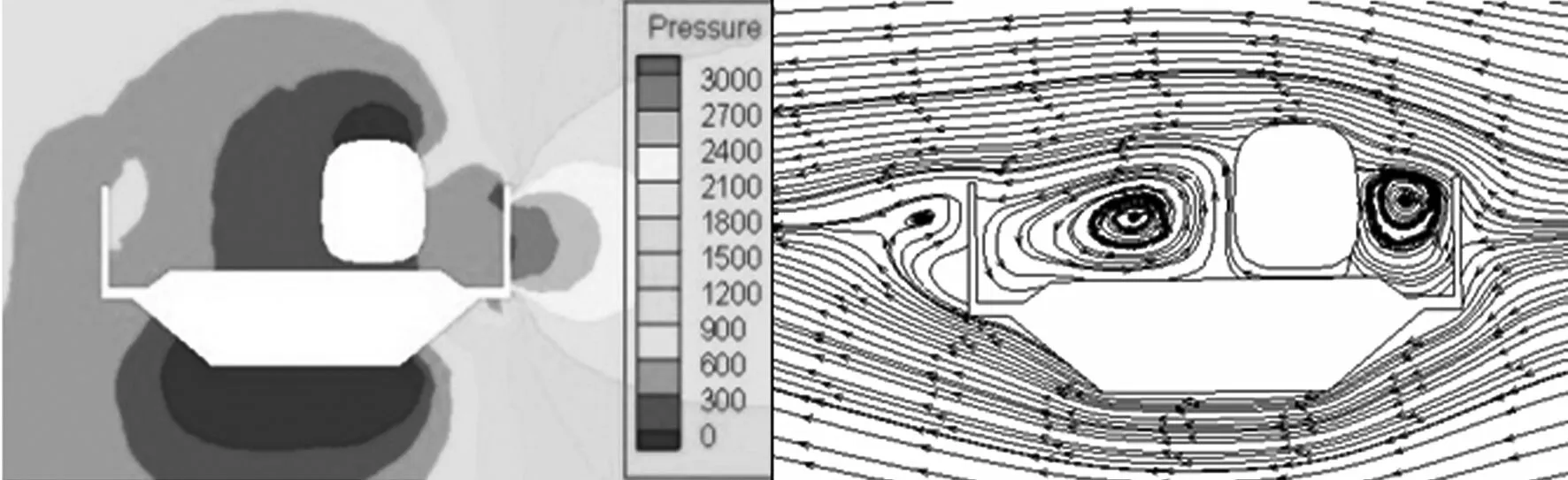
(a) 头车截面

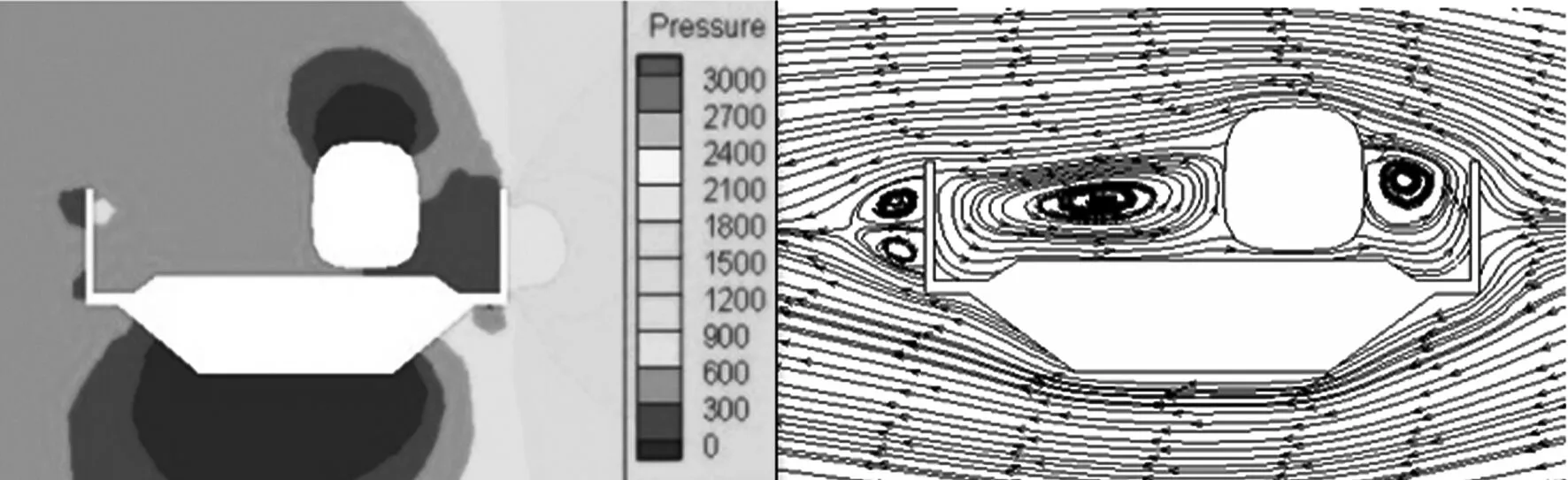
(b) 中间车截面

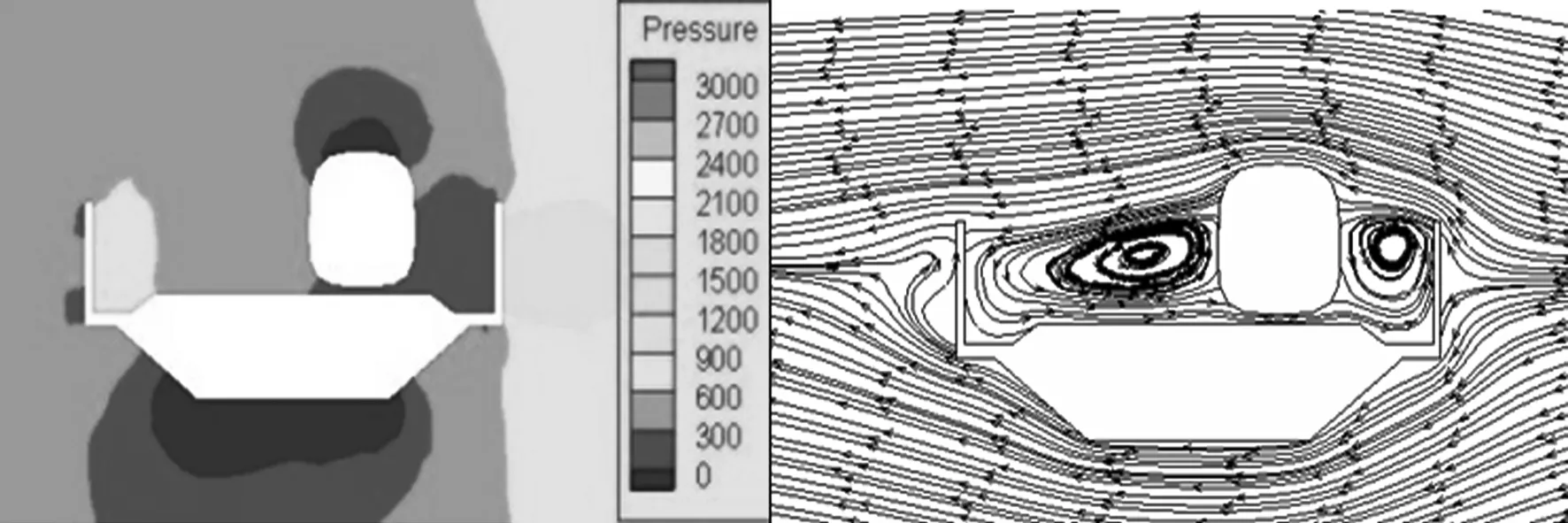
(c) 尾车截面

根据图9，高速列车的迎风侧与背风侧均为正压，只是在不同位置处压差有微小的变化.随着远离头车鼻尖处，迎风侧的压力逐渐减小.而在背风侧，随着远离头车鼻尖处，压力增加.

横向来流首先遇到风屏障的阻挡，来流被抬升，使车顶附近的流速增大.由于风屏障的存在，导致列车迎风侧和背风侧均形成了较大的漩涡，由漩涡形成的压差横向力可能对列车的气动性能起到主要的作用.

由头车、中间车、尾车的速度流线图对比可知，中间车和尾车由于处在横风及列车速度的合成速度的远端，湍流发展的空间更大，流场发展更为充分，形成的漩涡范围更大，即列车背风侧形成的漩涡区域头车最小，尾车最大.

表2为横风中列车在高架桥运行时各车所受到的气动力及气动力矩值.由该表可知，头车的横向气动力受横风的影响最为严重.

表2 各车气动力及气动力矩值

2.2 瞬态风作用下列车的气动特性

在高架桥加装风屏障后，列车周围的流场结构发生了改变，从而影响到列车的气动性能.下面重点分析高速列车头车的表面压力， 取列车的运行速度为300 km/h，风向角为90°，最大风速为23.46m/s，稳定风速为13.8 m/s，最小风速为4.14 m/s.图10为瞬态风作用下不同时刻头车的表面压力分布.

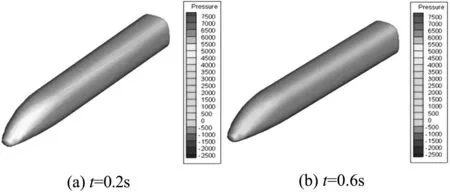
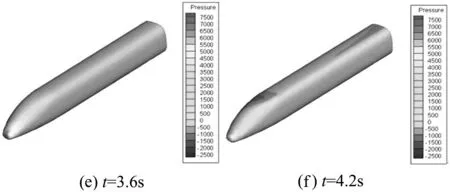
图10 瞬态风作用下列车头车表面的压力云图

由图10可知，瞬态风下列车表面的压力随时间变化而变化.在t=0.2s时横风风速为5.52m/s，由于风速数值较小，且流场发展未稳定，在风屏障作用下列车迎风侧与背风侧压力都为正压且相差不大，仅为1 700Pa左右；在t=0.6,t=2.6和t=4.2s三个时刻时，虽然标定风速值均为13.8m/s，但头车的表面压力云图却有明显差异，这是各时间点的前期风速值不同所致，即前一时刻风场的迟滞效应影响.t=2.6s时列车表面压差达到最大值8 500Pa，这是由于此刻正处于风速由最大值23.46m/s向最小值4.14m/s过渡时期，列车气动性能最为恶劣，流场压力分布较复杂；在t=1.6s时，风速达到最大值，由于风屏障的阻挡，气流大部分从车顶上风绕过，少部分气流会在车体两侧形成漩涡，此时车体表面迎风侧及背风侧均为负压；在t=3.6s时，风速达到极小值，车体表面压力分布较t=0.2s时复杂.

图11为不同时刻头车横截面的速度流线分布，可以更直观观察流场分布及漩涡所在位置.

同一横截面在不同时刻的速度流线图是不同的，随着时间的变化而变化.t=0.2s时， 列车迎风侧与风屏障形成出现漩涡，列车背风侧气流正常通过；在t=0.6,t=2.6和t=4.2s三个时刻时，虽然标定风速值均为13.8m/s，但速度流线图却呈现出延后性，即与各自的前一时刻的流线图类似.随着时间推进，与恒定风场的流线图相比，不同时刻的背风侧的漩涡的几何尺寸和位置均发生变化，且每个时刻的流线图也不相同.可见，在整个过程中列车的周围流场在瞬态风场下是不稳定的.

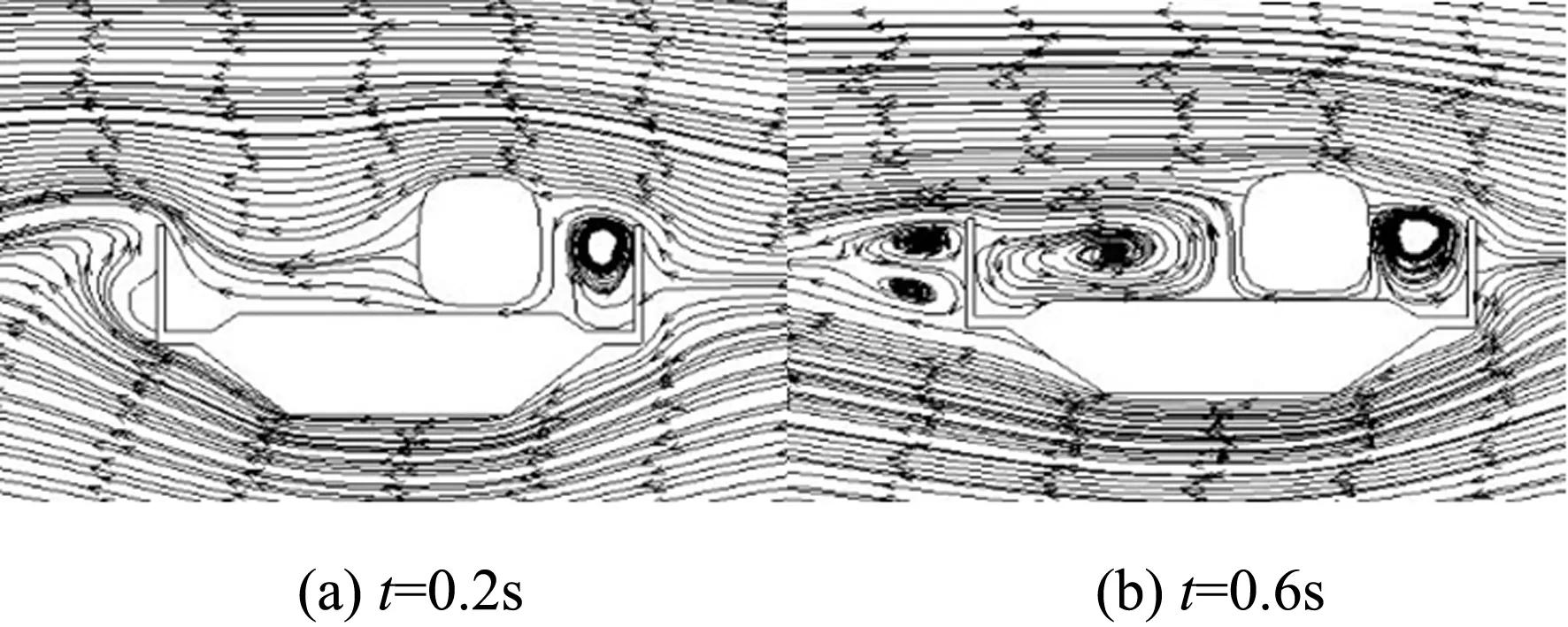
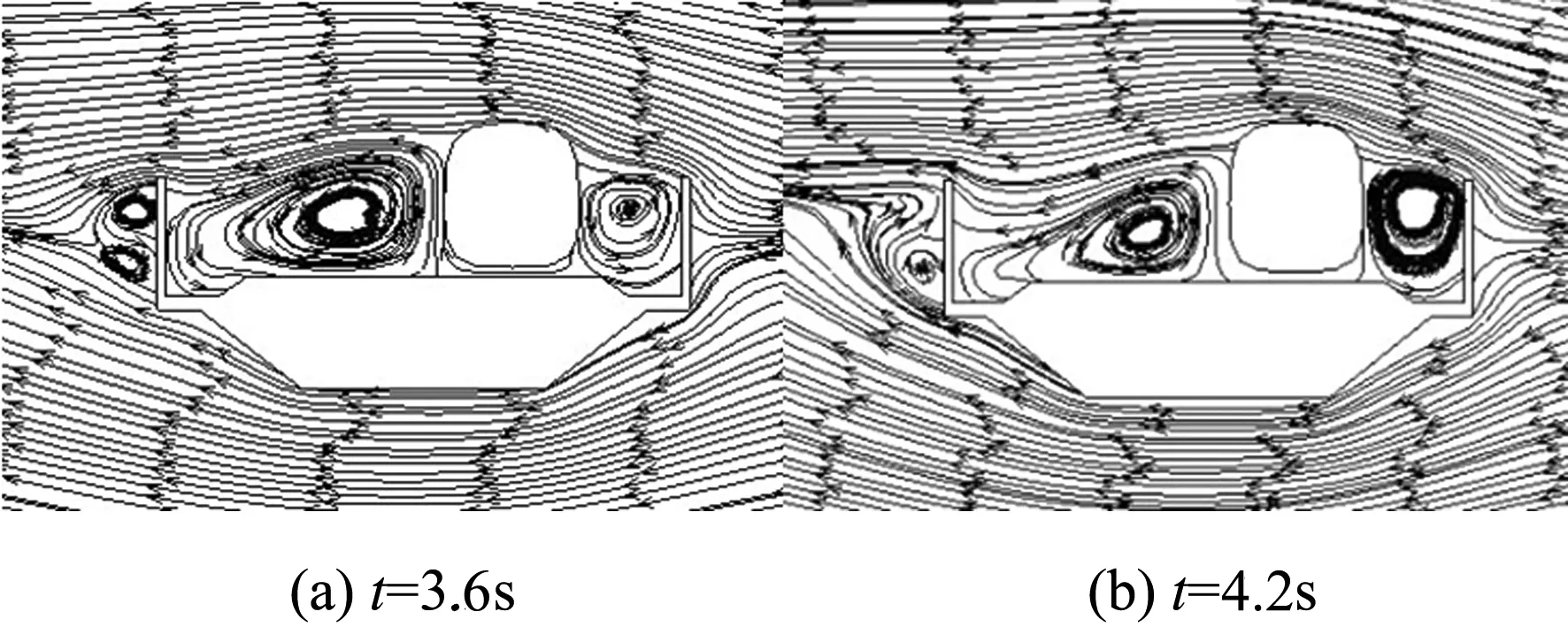
图11 瞬态风作用下列车头车横截面速度流线图

由以上分析可知，在瞬态风作用下，列车头车周围流场情况最为复杂，头车的气动载荷变化最明显，运行安全性最差.因此，有必要分析列车头车所受到的气动力和气动力矩随时间变化关系，如图12所示.

瞬态风场中列车受到的气动力受风速值的影响显著.由图12(a)可知，在瞬态风速作用下，气动阻力和侧向力的非稳态变化规律基本相同，瞬态风速值的波动对二者的影响明显比对升力影响大.图12(a)中，在0～1s内，由于风速在前0.5s内迅速增长，在后0.5s内维持恒值不变，阻力，升力和侧向力变化由急到缓；在1～2s内，风速经历了由恒值向最大值的波动过程，所以导致气动力也经历了由大到小的变化过程；在2～3s内，风速维持恒值不变，在考虑到各气动力响应滞后因素的前提下，各气动力保持大致恒定；在3～4s内，风速经历了第二次波动，此过程与第一次波动类似，不再赘述；在4s之后风速维持恒定，各气动力才逐渐趋于稳定.

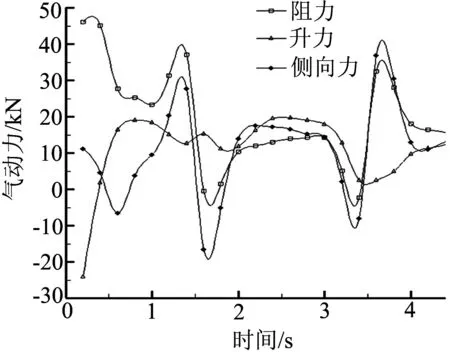
(a)气动力随时间变化

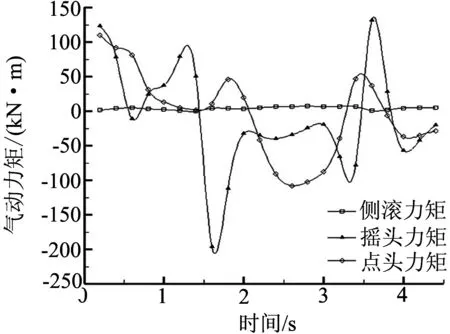
(b)气动力矩随时间变化

由图12(b)可知，点头力矩和摇头力矩则受风速值影响明显，且表现出与气动力类似的特征，即在时间上有明显的延迟性.

2.3 瞬态风作用下车速对列车气动载荷影响

以下分析高速列车以不同速度通过带有风屏障的高架桥时车速对列车所受气动载荷的影响.瞬态风场的风速值仍按图5所示的规律变化，列车分别以200、250、300、350和400km/h通过计算区域时，列车头车所受到的气动力和气动力矩随时间变化的曲线如图13所示.

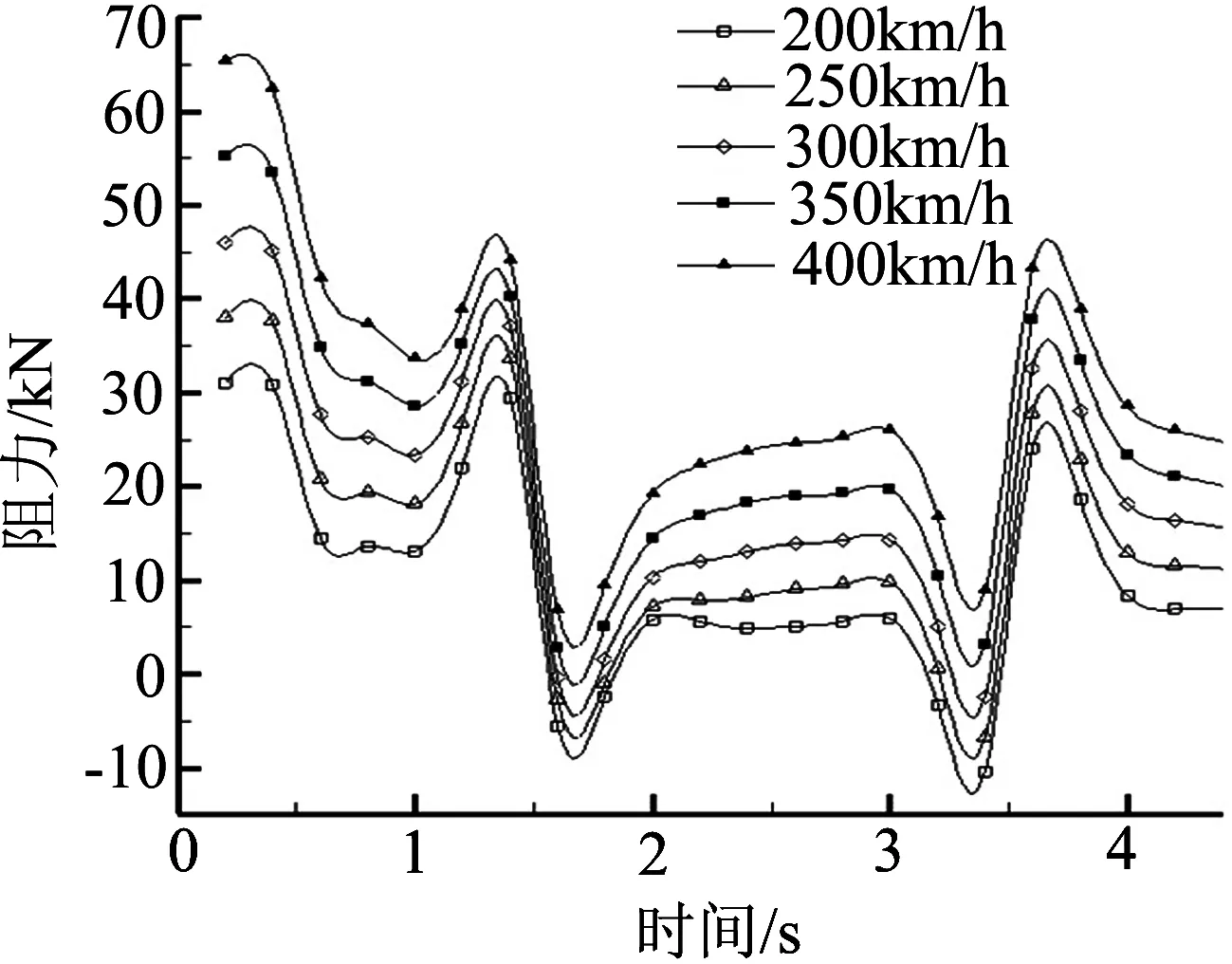
(a)气动阻力变化曲线

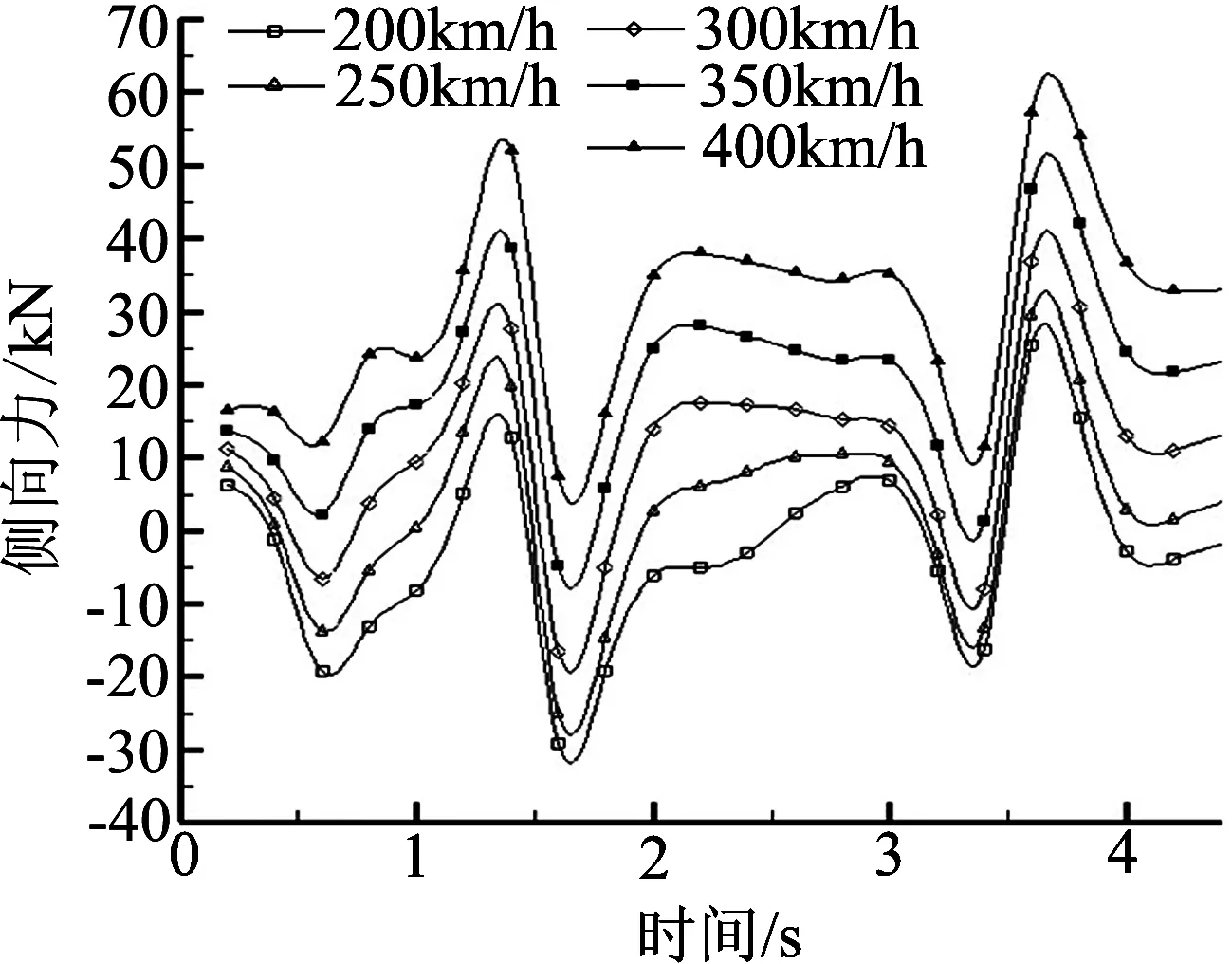
(b)侧向力变化曲线

由图13可看出，在瞬态风作用下，同一时刻随着车速增加，列车运行的气动阻力和侧向力均相应增加，表现出明显的正相关性.车速由200km/h以50km/h的增幅逐渐递增到400km/h时，列车运行的最大气动阻力增长率分别为9.82%、10%、8.83%和9.13%.表明，在瞬态风作用下带风屏障的高架桥上，车速的变化不会对周围流场结构产生明显变化，但会明显改变列车所受的气动载荷.

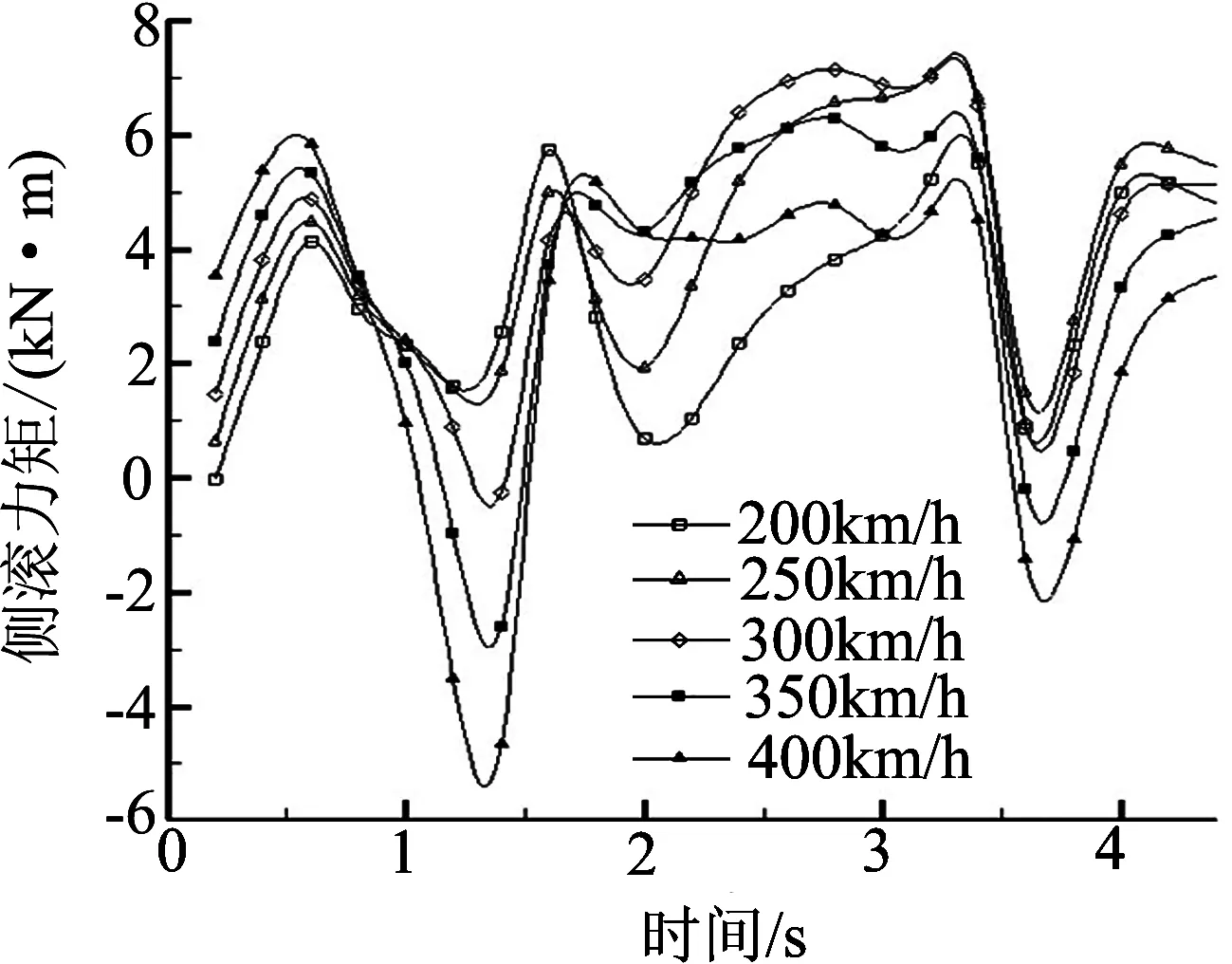
图14 不同车速下头车的侧滚力矩变化历程

图14表明，车速的变化对侧滚力矩影响很大.列车的侧滚力矩同时受到瞬态风风速和列车运行速度的影响，在瞬态风风速值变化过程中，虽然风向保持为90°，但列车运行的侧滚力矩方向随风速值而发生改变.在不同车速范围内，影响侧滚力矩的主要因素不同，当列车运行速度小于250km/h时，侧滚力矩幅值随瞬态风风速值变化而变化，表现出幅值大小不随车速的变化而变化；当列车运行速度大于250km/h时，车速是影响列车侧滚力矩变化的主要因素，由图中1～2s图像可以看出，对应车速300、350和400km/h时的侧滚力矩幅值变化依此增大，且增大幅度比例升高，不再表现出车速小于250km/h，侧滚力矩变化趋势基本不受车速影响，所以建议列车运行安全车速小于250km/h.

3 结论

(1)恒定侧风下头车周围的流场结构最为复杂.表现为头车的横向气动力受横风的影响最为严重，当车速为300km/h，横风风速为13.8m/s，头车受到的横向力是中间车的3.6倍，是尾车的4.9倍;

(2)恒定风场下，列车所受到气动力基本稳定不变，而中国帽型瞬态风作用下高速列车的气动性能表现出明显的延时性;

(3)平均风速值相同情况下，中国帽型瞬态风场下高速列车的运行安全性比恒定风场下差得多.当列车以300km/h运行在有风速波动的时域范围，列车所受到的气动力及气动力矩均发生明显波动;

(4)中国帽型瞬态风场下，车速对列车受到的气动力和气动力矩的影响规律不同.车速由200km/h以50km/h的增幅逐渐递增到400km/h时，列车运行的最大气动阻力增长率均在9%～10%，而侧滚力矩的增幅则越来越大，这表明列车运行速度越高，稳定性越差.

[1]罗建斌，杨志刚．高架桥声屏障高度对高速列车气动特性的影响[J]．计算机辅助工程，2011，20(3)：6-10.

[2]WETZEL C, PROPPE C. Crosswind stability of high-speed trains: a stochastic approach[C]. BBAA VI International Colloquium on: Bluff Bodies Aerodynamics & Applications, Milano, Italy, 2008:20-24.

[3]CARRARINI A. Reliability based analysis of the crosswind stability of railway vehicles. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(7): 493-509.

[4]于梦阁, 张继业,张卫华.随机风作用下高速列车的非定常气动载荷[J].机械工程学报, 2012,48(20):113-120.

[5] PROPPE C, WETZEL C. A probabilistic approach for assessing the crosswind stability of ground vehicles[J]. Vehicle System Dynamics, 2010, 48(1)：411-428.

[6] CARRARINI A. Reliability based analysis of the cross wind stability of railway vehicles [D]. Berlin：Technical University, 2006.

[7]毛军,郗艳红,杨国伟. 侧风风场特征对高速列车气动性能作用的研究[J].铁道学报,2011,33(4):22-30.

Aerodynamic Characteristics of High-Speed Train Runing on a Viaduct with Wind Barriers under in Transient Wind

WU Chao, DU Liming

(School of Traffic and Transportation Enginerering, Dalian Jiaotong University, Dalian 116028)

Aerodynamic performances of high-speed train runing on a viaduct with wind barriers in Chinses-hat transient wind was numerically investigated. The data were compared with those produced in constant crosswind. The results show that the flow field of the first carriage is the most complicated among the whole high-speed train and the aerodynamic loads change most significantly in the constant crosswind. While in transient wind, the aerodynamic performances of the high-speed train show some certain time lag. When the train speed is 300km/h, the aerodynamic forces and aerodynamic moments of the trains fluctuate significantly during wind speed increasing from 13.8 m/s to 23.46 m/s, then declining to 13.8 m/s. The phenomenon is significantly different from the constant lateral force of the train running in steady crosswind. When the train running in speed between 200 km/h and 400 km/h, the maximum aerodynamic resistance of the train increases 9-10% for every increase in the speed 50 km/h, and the other aerodynamic forces steadily increase with the train speed. It also indicates that the increasing amplitude of aerodynamic torques obviously increase with the train speed.

natural transient wind; high-speed train; wind barriers on viaduct; aerodynamic characteristics; numerical analysis

1673- 9590(2017)02- 0021- 07

2016-03-12

吴超(1989-)，男，硕士研究生; 杜礼明(1972-)，男，博士，教授，主要从事机车车辆流体动力学方面的研究

A

E- mail:dlm@djtu.edu.cn.