肿瘤治疗参数对超声空化影响数值分析
沙智华,张晨博,马付建,刘宇,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028)*
肿瘤治疗参数对超声空化影响数值分析
沙智华,张晨博,马付建,刘宇,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028)*
通过分析气泡初始半径对频率和声压阈值的影响,选取了频率和声压范围.建立单一气泡的超声空化运动模型,通过数值分析的方法,研究超声频率、超声振幅和气泡初始半径等因素对超声空化的影响,结果表明:随着超声振幅和气泡初始半径的增大及超声频率和表面张力系数的减小,气泡的振动幅度越大,气泡空化时产生的压强越大.
肿瘤;超声空化;声压阈值;频率阈值;运动学模型
0 引言
恶性肿瘤作为威胁人类生命的主要疾病,已经成为21世纪人类的第一杀手.传统的手术、化疗和放疗等治疗方法存在明显的毒副作用[1].所以高效的微创肿瘤治疗方法已成为新的研究方向,目前肿瘤超声治疗方法是一种主要的微创肿瘤治疗方法.该方法利用超声空化效应,使肿瘤血管中注射的微泡剂中气泡瞬间崩溃,释放高温高压,致血栓以堵塞肿瘤血管,切断肿瘤细胞的营养供给而坏死,从而达到治疗的目的[2].
超声空化的剧烈程度直接影响着肿瘤治疗的效率和效果,目前学者们针对超声空化做了一定的研究.刘秀梅等[3]通过数值模拟的方法研究液体的不同表面张力对超声空化的影响.Xi等[4]研究表明气泡空化情况受声压和初始半径的影响较大.Chakma等[5]研究发现在环境压力一定时,空化气泡的半径越小,则崩溃时产生的较高的声压.张凤春等[6]通过对53例实体肿瘤患者临床治疗发现,超声空化治疗实体肿瘤的效果较好.目前针对超声空化作用理论的研究已取得一定的成果,但针对肿瘤超声治疗的相关研究很少,且主要以临床试验为主.
本文以单一气泡为研究对象,建立气泡的运动学模型,并利用MATLAB对气泡运动模型进行数值求解,分析不同肿瘤超声治疗参数对血液和微泡剂混合液中气泡空化的影响.
1 气泡空化声压和频率阈值
1.1 气泡声压阈值
空化的产生,需要一定的外界扰动来破坏气泡的平衡态.当超声场对液体的声压幅值大于液体静压力,并且克服液体的表面张力时,才会产生空化作用,能使液体产生空化作用的最低超声声压幅值即为声压阈值.声压阈值Pt可表示为[7]
(1)
式中,σ为液体的表面张力系数,P0为液体静压力,R0为气泡初始半径.
在37℃的人体血液与微泡剂混合液中,液体静压力P0=1.013×105Pa,混合液表面张力系数σ=6×10-2N/m,通过对式(1)进行数值分析可得气泡初始半径R0与声压阈值Pt的的关系如图1所示.
由图1可以看出,当气泡初始半径接近0μm时,气泡空化时所需的声压阈值很大,随着气泡初始半径R0的接近1μm时,声压阈值迅速下降,当R0从1μm增大到5μm时,声压阈值下降缓慢,当R0从5μm增大到25μm时,声压阈值下降趋于平稳,因此气泡初始半径越小,需要的声压阈值越大.
1.2 气泡频率阈值
空化气泡在超声场下作用时,气泡壁随着超声作用不断的膨胀或者压缩,但不一定会发生崩溃.当超声频率大于气泡的共振频率时,气泡一般不发生崩溃,因此气泡空化时超声波产生的最大频率被称为频率阈值.频率阈值fa公式为[8]:
(2)
式中,k为气体的多变指数,ρ为液体密度,P为气泡受超声作用下的压力.
在37℃人体血液与微泡剂的混合液中,气泡周围受到的超声压力P=2.9×106Pa,混合液表面张力系数σ=6×10-2N/m,混合液中气体多变指数k=1.33,混合液液体密度ρ=1 050kg/m3时,由式(2)通过数值分析可得微泡剂中气泡的初始半径R0与频率阈值fa的关系如图2所示.
由图2可以看出,随着气泡初始半径R0的趋近于0μm时,所需的频率阈值越大,并且随着气泡半径逐渐增大接近于5μm时,频率阈值迅速下降,当R0由5μm增大到25μm时,频率阈值下降缓慢,因此空化泡初始半径越大,需要的频率阈值越小.
本文对气泡的初始半径分析的范围为5~25μm,由图1和图2可知气泡的声压阈值和频率阈值随着气泡半径的增大而减小,因此在气泡的取值范围内应当选取气泡初始半径最小值为5μm时的声压阈值1.058×105Pa和取值范围内气泡初始半径的最大值25μm时的频率阈值69kHz,可以满足对气泡初始半径范围为5~25μm时声压阈值和频率阈值的要求,即在以下的气泡空化的数值分析时,超声振动系统产生的声压需大于1.058×105Pa,超声治疗仪产生的超声频率应小于69kHz.
2 超声气泡空化运动
2.1 单一气泡的超声空化运动学方程推导
假设单一气泡在超声场作用下半径由R0扩张到R1时,如图3所示,气泡内存在饱和蒸汽压力Pv和泡内气体压力Pg,气泡外受到在超声作用下的超声压力PA,液体静压力P0,气泡表面阻碍气泡膨胀的表面张力Pσ,以及气泡膨胀时液体的粘滞力Pμ共同作用时产生的边界合力P(R).即气泡在超声场作用时,气泡内外的压力合力相等P(R)为
(3)
液体的粘滞力Pμ为[11]
(4)
式中,R为气泡的瞬时半径,μ为液体的粘滞系数.
表面张力为Pσ为[11]
(5)
实际泡内气体压力Pg方程[9]为
(6)
在肿瘤治疗过程中,一束超声波作用在气泡周围,对气泡产生的声压PA的方程为
(7)
式中,A为超声振幅,v为超声波在液体中的速度,ω为超声角频率.
由Rayleigh单泡运动学微分方程[10]可知,在气泡内外压平衡时,气泡的运动方程为
(8)
将方程(3)~(7)代入方程(8)中,在考虑到气泡内的饱和蒸汽压Pv时,可得到实际气体的单泡空化动力学方程为
(9)
由式(9)可知,气泡在一个空化周期内存在最大半径Rmax和最小半径Rmin,气泡崩溃时产生的压强Pmax与最大半径和最小半径的关系为[11]
(10)
2.2 结果与分析
人体血液与微泡剂的混合液在37℃时的液体静压力、粘度系数、液体密度、超声声速、饱和蒸汽压等环境参数如表1所示.

表1 环境参数
2.2.1 超声振幅对空化的影响
在超声频率f=40kHz,混合液的表面张力系数σ=6×10-2N/m,混合液气泡初始半径R0=15μm,超声振幅A分别为1、4、7、10和13μm时(图4中对应曲线1~5),通过数值分析方法得到的气泡半径随时间的变化曲线如图所示.取一个空化周期的气泡半径最大值Rmax和半径最小值Rmin,由式(10)计算气泡空化瞬间产生的压强如图5所示.
由图4可知,随着超声振幅A的增加,气泡的最大半径随之增大,气泡的最小半径基本保持不变,因此气泡的振动幅度随着超声振幅A的增大而增加,同时气泡空化的时间t随着超声振幅A的增大而延长.由图5可知,气泡空化瞬间产生的压强随着超声振幅的增大而增大,这是由于随着超声振幅的增加,超声波作用于液体时产生的压强随之增大,在超声负压区,气泡受到的拉伸作用增强,在超声正压区,气泡受到更强的压缩力,使气泡空化瞬间产生更大的压强.

图4 振幅不同时气泡半径随时间的变化曲线
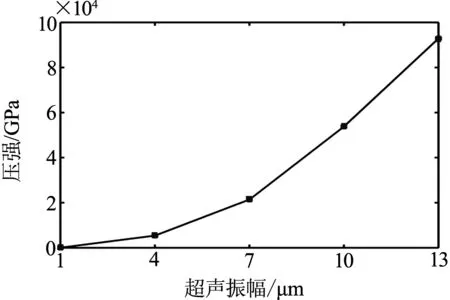
图5 气泡空化瞬间产生的压强随超声振幅的变化曲线
2.2.2 超声频率对空化的影响
在超声振幅A=7μm,混合液表面张力系数σ=6×10-2N/m,混合液气泡的初始半径R0=15μm,超声频率f分别为20、30、40、50、60kHz(图6中对应曲线1~5)时,通过数值分析频率对气泡空化的影响如图所示, 取一个空化周期的气泡半径最大值Rmax和半径最小值Rmin由式(10)计
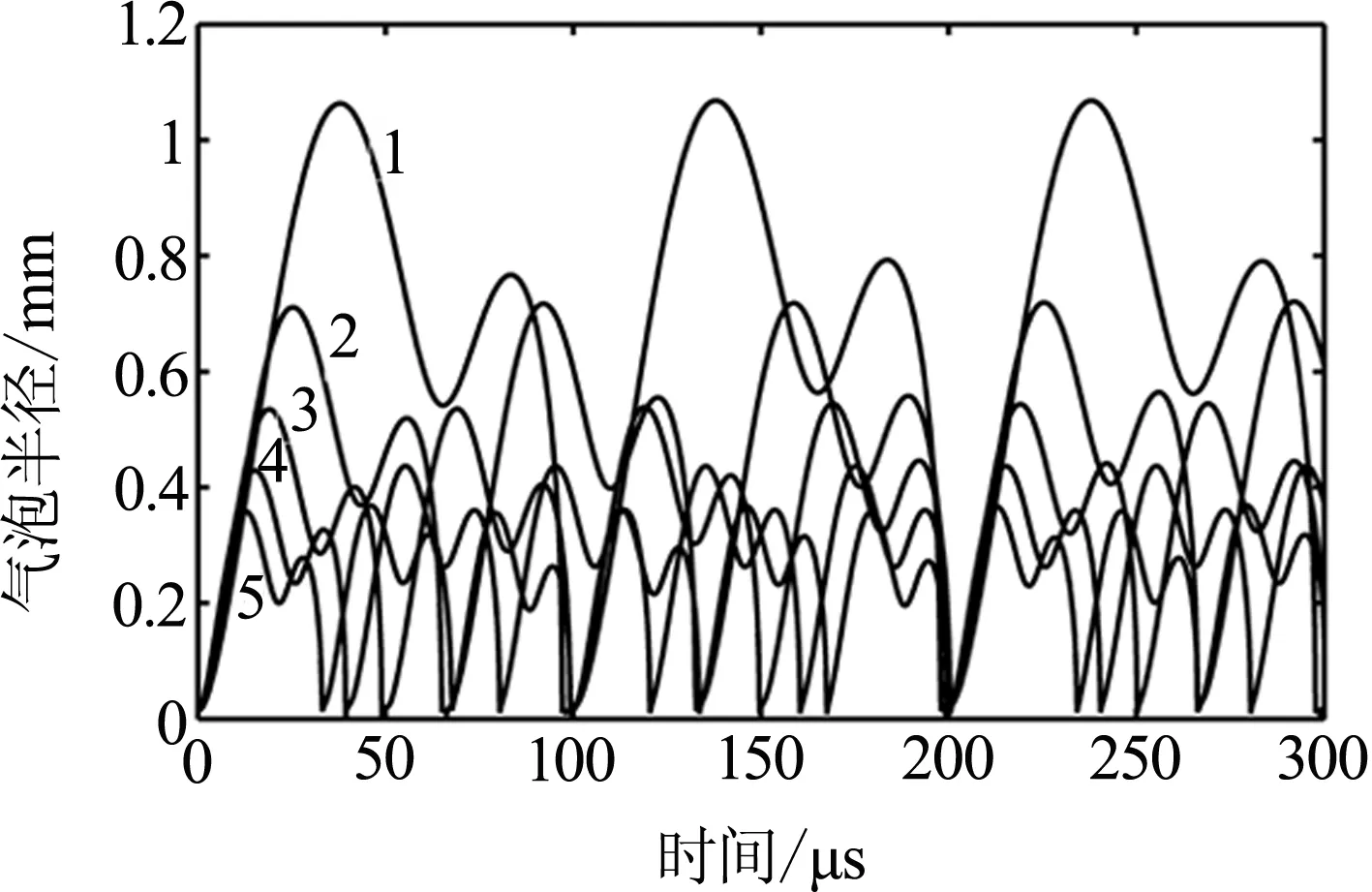
图6 超声频率f不同时气泡半径随时间的变化曲线

图7 气泡空化瞬间产生的压强随超声频率的变化曲线
算气泡空化瞬间产生的压强如图7.
从图6可以发现,超声频率为20 kHz时气泡的振动幅度最大,并且随着超声频率f的增加,气泡的振动幅度在逐渐减小.从图7中可发现,当超声频率为20kHz气泡崩溃时产生的压强最大,并且随着频率的增加气泡空化时产生的压强迅速减小,这是由于随着超声频率的增大,空化周期变短,气泡随超声作用下膨胀时间变短,从而导致气泡最大振幅减小,使得气泡空化时最大压强减小.
2.2.3 气泡的初始半径对空化的影响
在超声频率f=40kHz,混合液的表面张力系数σ=6×10-2N/m,超声振幅A=7μm,混合液中气泡初始半径R0分别为5、10、15、20、25μm(图8中对应曲线5~1)时,通过数值分析的方法得到气泡半径随时间的变化曲线如图8所示,取一个空化周期的气泡半径最大值Rmax和半径最小值Rmin由式(10)计算气泡空化瞬间产生的压强如图9.
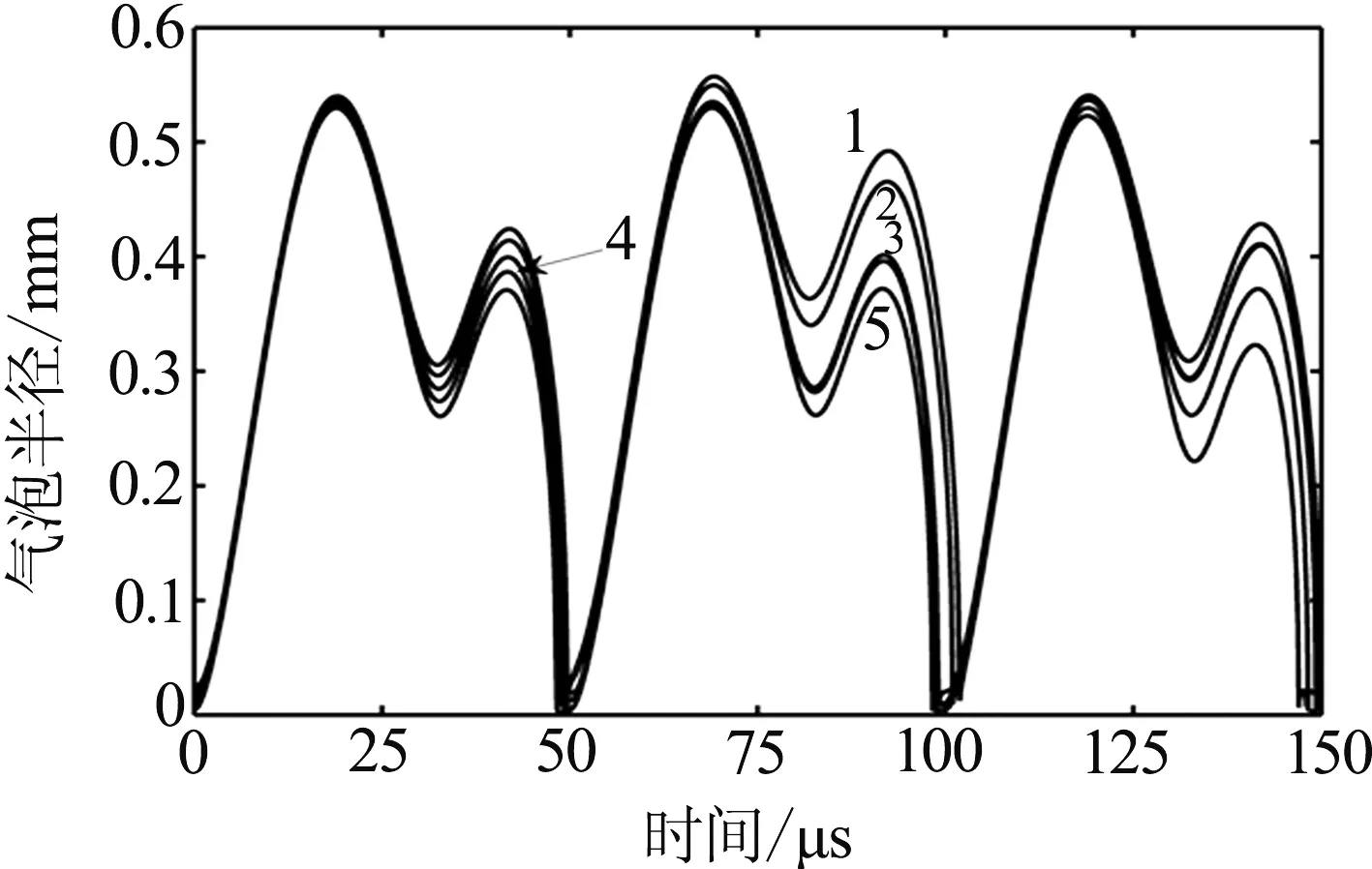
图8 初始半径R0不同时气泡半径随时间的变化曲线
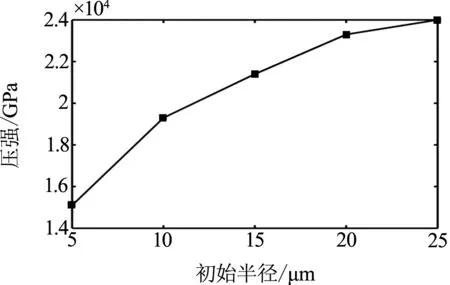
图9 气泡空化瞬间产生的压强随气泡半径的变化曲线
由图8可知在其他参数保持不变的情况下,随着混合液中气泡的初始半径R0的增加,在超声的作用下气泡的振动幅度逐渐增加,但是增加不明显.通过图9分析可知初始半径为5μm的产生的压强最小,随着气泡初始半径的增大,气泡空化时产生的压强也随之增大,并且随着气泡半径的增大,气泡空化时产生的压强趋于平缓.
2.2.4 气泡表面张力系数对空化的影响
在超声频率f=40kHz,混合液气泡初始半径R0=15μm,,超声振幅A=7μm.由于超声微泡剂的不同,其与血液混合后的混合液表面张力也不相同,通混合液的表面张力系数σ分别为2×10-2、4×10-2、6×10-2、8×10-2、1×10-1N/m,通过数值分析,得到气泡半径随时间的变化关系如图10所示,然后取一个空化周期的气泡半径最大值Rmax和半径最小值Rmin由式(10)计算气泡空化瞬间产生的压强如图11.
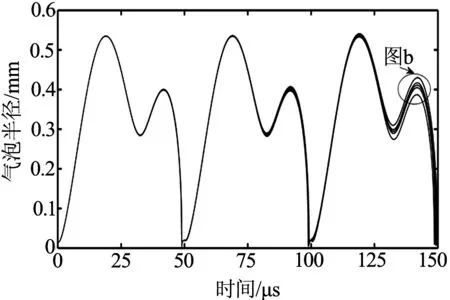
(a)表面张力系数随时间的变化曲线
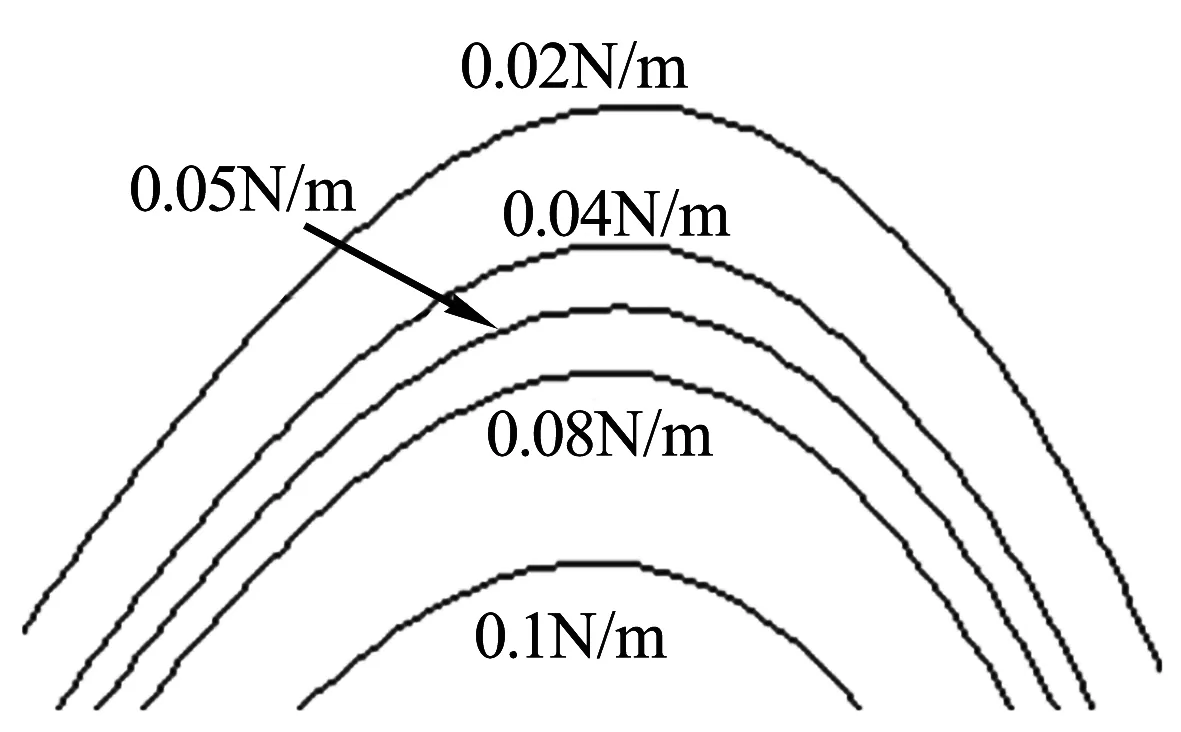
(b)波峰放大图
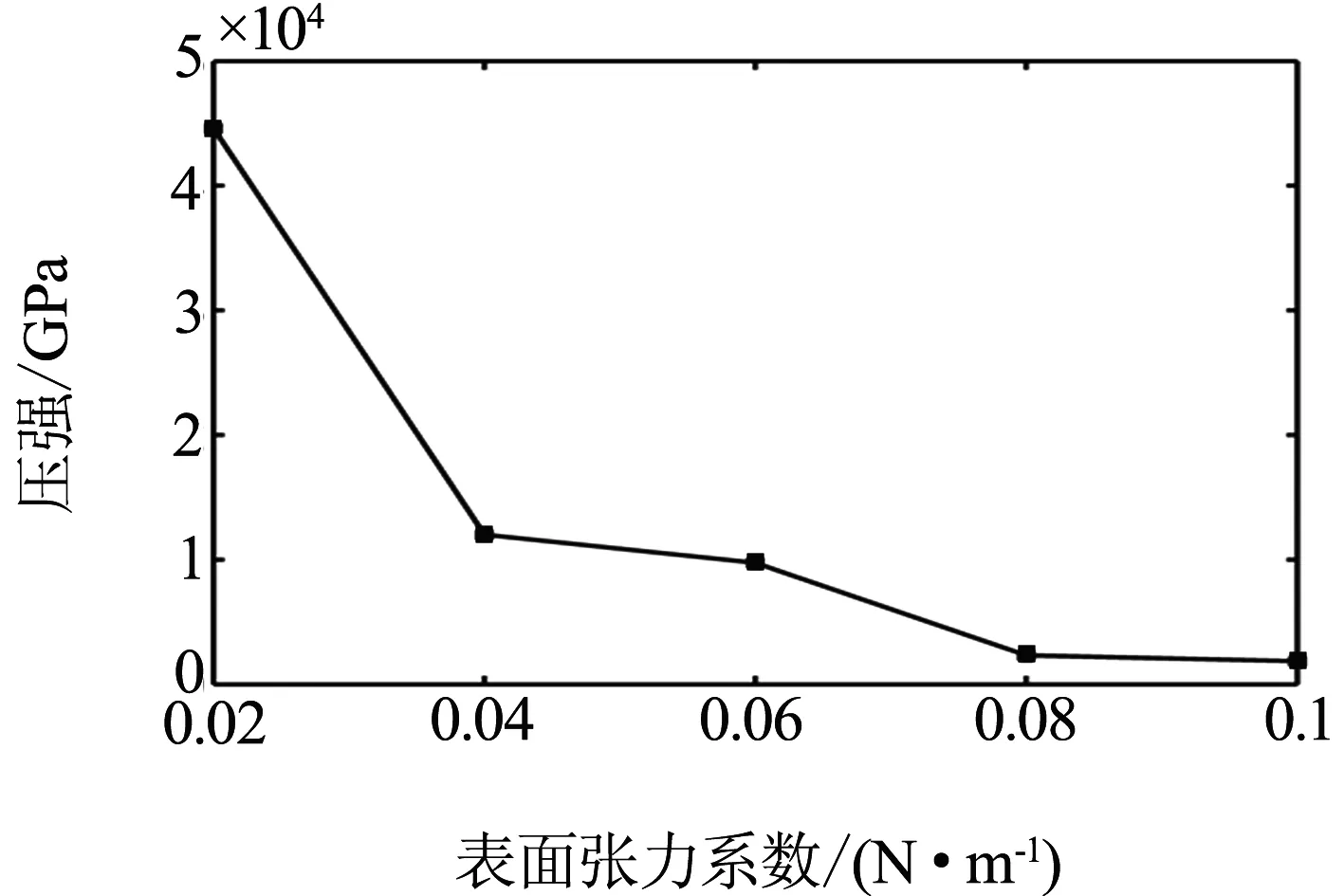
图11 气泡空化瞬间产生压强随表面张力系数的变化曲线
图10可以发现,随着混合液表面张力系数的降低,气泡的振动幅度随之升高,即气泡的的最大半径在增大.从图11可以看到当表面张力系数越低气泡空化瞬间产生的压强越大,当表面张力系数从2×10-2N/m增加到4×10-2N/m时,气泡空化产生的压强急剧下降,而当表面张力系数从8×10-2N/m增加到1×10-1N/m时气泡空化产生的压强下降缓慢,由此可知表面张力系数越大,气泡空化瞬间产生的压强越小.
3 结论
以单一气泡为研究对象,建立了超声场下气泡在液体中的空化运动学模型,分析在血液与微泡剂混合液中气泡空化所需的声压和频率阈值,研究不同超声振幅、超声频率、气泡初始半径和表面张力系数对超声空化的影响结论如下:
(1)通过分析在肿瘤超声治疗中选定的初始气泡半径范围内气泡空化时所需的声压和频率阈值,得到了气泡空化时所需的超声频率需小于69kHz,所需的超声声压最小值为1.058×105Pa;
(2)随着超声振幅和气泡初始半径的增大及超声频率和表面张力系数的减小,气泡的振动幅度越大,气泡空化时产生的压强越大;
(3)通过对比不同超声振幅、超声频率、气泡初始半径和表面张力系数产生的气泡空化压强发现,超声振幅对超声空化影响最大,依次为表面张力系数、超声频率和气泡初始半径.
[1]汤钊猷.现代肿瘤学[M].2版,上海:上海医科大学出版社,2000.
[2]吴巍,陈宏,李荣清,等.低功率超声栓塞肿瘤新生血管治疗肿瘤的临床研究[J].中国介入影像与治疗学,2005 (6):418- 421.
[3]刘秀梅,贺杰,陆建,等.表面张力对固壁旁空泡运动特性影响的理论和实验研究[J].物理学报,2009 (6):4020- 4025.
[4] XI X , CEGLA F B , LOWE M, et al. Study on the bubble transport mechanism in an acoustic standing wave field[J]. Ultrasonics, 2011,51(8):1014-1025.
[5]CHAKMA S, MOHOLKAR V S.Mechanistic features of ultrasonic desorption of aromatic pollutants[J].Chemical Engineering Journal,2011(22): 356-367.
[6]张凤春,左丽,王红霞,等.低功率超声空化治疗肿瘤的临床研究[J].肿瘤, 2011(2):160-164.
[7]李争彩,林书玉.超声空化影响因素的数值分析模拟研究[J].陕西师范大学学报(自然科学版),2008(1):37- 42.
[8]郭林伟,李成荣.超声空化动态研究进展[J].榆林学院学报,2008(6):44- 45.
[9]王捷.单一超声空化气泡动力学过程的数值分析[D].陕西:陕西师范大学,2006.
[10]RAYLEIGH L.On the pressure developed in a liquid during the collapse of a spherical cavity[J]. Philosophical Magazine, 1917,34(6):94-98.
[11]冯若.超声手册[M].南京:南京大学出版社,2001.
Numerical Analysis of Tumor Treatment Parameters on the Effect of Ultrasonic Cavitation
SHA Zhihua, ZHANG Chenbo, MA Fujian, LIU Yu, ZHANG Shengfang
(School of Mechanical Engineering, Dalian Jiaotong University, Dalian 116028, China)
The frequency and sound pressure ranges were selected through analyzing the influence of initial bubble radius on frequency and sound pressure threshold. Ultrasonic cavitation motion model of single bubble was established. The influences of the ultrasonic frequency, ultrasonic amplitude and initial bubble radius on ultrasonic cavitation were discussed by numerical analysis. The results show that the vibration amplitude of the bubble and the pressure generated by the bubbles cavitation is increasing with increasing the ultrasonic amplitude and the initial bubble radius, as well as the decreasing of ultrasonic frequency and the surface tension coefficient of mixture.
tumor; ultrasonic cavitation; sound pressure threshold; frequency threshold; motion model
1673- 9590(2017)02- 0058- 05
2016-03-11 基金项目:辽宁省教育厅优秀人才计划资助项目(LR2015012);辽宁省自然科学基金资助项目(2015020114);大连市科技计划资助项目(2015E11SF051)
沙智华(1973-),女,教授,博士,主要从事难加工材料加工技术的研究
A
E- mail:zhsha@djtu.edu.cn.

