IN718合金热机械疲劳试验非稳态温度场的数值模拟

陈继光，邓文凯，周 萍，江 亮



IN718合金热机械疲劳试验非稳态温度场的数值模拟

陈继光1, 2，邓文凯3, 4，周 萍1, 2，江 亮3, 4

(1. 中南大学能源科学与工程学院，长沙410083；2. 中南大学流程工业节能技术湖南省重点实验室，长沙410083；3. 中南大学粉末冶金国家重点实验室，长沙410083；4. 中南大学粉末冶金研究院，长沙410083)

基于热机械疲劳试验，建立IN718高温合金感应加热过程中电磁场和温度场耦合的数学模型，对试样在循环加热条件下的非稳态温度场进行仿真，采用电子背散射衍射技术对试样上的晶粒尺寸进行检测并对其数据进行统计分析。结果表明：综合传热系数和风机电压呈正相关的关系；试样径向上存在温度梯度且随时间变化，最大温差为5 ℃左右，符合试验要求；低周疲劳试样径向上不同点的平均晶粒尺寸均有所增长，且增长幅度基本相同；由于温度梯度的影响，热机械疲劳试样径向上的晶粒尺寸分布不均匀，中心位置和表面位置的平均晶粒尺寸增长幅度分别为16.94%和5.3%。

高温合金；热机械疲劳；感应加热；温度梯度；晶粒尺寸

航空航天技术的迅猛发展对材料的性能提出了更高的要求，高温合金因具有良好的抗氧化、抗腐蚀性能，优异的拉伸、持久、疲劳性能和长期组织稳定性而成为制造航空航天设备的关键材料[1]。疲劳性能则是表征高温合金材料疲劳寿命的重要技术指标，成为高温合金材料领域的研究热点。

关于疲劳性能的研究主要分为等温疲劳与热机械疲劳两大类。针对等温疲劳，黄志伟等[2]对镍基高温合金在高温下的低周疲劳(LCF)性能进行了研究，分析了应力和应变幅值对裂纹萌生和断裂机制的影响。MURAKAMI等[3]研究了不同应力下表面裂纹对材料延展性和疲劳寿命的影响。KABIR等[4]和王媛媛等[5]探讨了不同温度对材料LCF性能的影响。

由于高温合金材料常工作于温度与机械载荷同时变化的环境中，等温疲劳不能同时表征温度载荷对材料形变的影响，因此，热机械疲劳(TMF)越来越得到相关研究人员的关注。徐涛等[6]基于TMF试验提出了一种适用于镍基单晶高温合金TMF的本构模型，分析了晶体取向对材料TMF性能的影响。REDDY等[7]对比了试样在TMF和LCF试验中疲劳寿命和材料成分的关系。王留兵[8]和张国栋等[9]利用微裂纹扩展模型、Manson-Coffin方程和拉伸迟滞能模型对材料TMF寿命进行了预测。

在TMF试验中，试样温度的精确控制对保障试验结果的有效性非常重要。TMF试验假定试样内部温度均匀，因此，对试样尺寸以及径向最大温差均有着严格的规定。实际上，试样在循环热载荷的作用下，其内部的温度分布受试样的材质、尺寸以及外部冷却方式等因素的影响，而TMF试验仅能通过检测试样表面温度对其温度进行调节，无法直接获取试样内部温度信息，不能确定试样中最大温差是否能满足TMF试验的要求。

本文作者拟采用数值模拟的方法预测IN718高温合金在TMF试验过程中的温度分布，为试验系统中加热与冷却装置的设计与操作提供理论依据，以提高TMF的有效性；同时试样冷却过程中综合传热系数受冷却方式、试样温度等因素的影响，是TMF试验装置设计以及试样温度场模拟的关键参数。在此，拟基于试验数据与迭代算法，获得试样冷却过程综合传热系数数值，为高温合金材料TMF试验提供基础。

1 热机械疲劳试验

1.1 试验装置和材料

本试验中依据ASTM E606/E606M−12[10]进行设计。考虑到感应加热具有热效率高、易于实现自动控制和局部加热等特点，以及风冷方式具有综合传热系数调节灵活的特点，采用感应加热与风冷方式。图1(a)所示为MTS810热机械疲劳试验控制系统示意图，主要包括感应加热装置、风机冷却装置、液压传动装置、数据采集装置和计算机控制系统。

TMF试验材料选用IN718高温合金，其物理参数如表1所列。为了防止表面加工划痕的影响，对试样标距(19.05mm)区域进行抛光处理，试样的几何尺寸如图1(b)所示。

1.2 试验过程

在TMF试验过程中，设定试样的应变循环和温度循环频率相同且为同相位，应变幅值为1.2%，周期为120 s，结果如图2(a)所示。通过感应线圈加热使试样从室温下迅速升高到500 ℃，短暂均温后，通过计算机闭环控制系统调节感应加热电源输出功率和风机电压，使试样表面温度呈现周期性变化，温度变化范围为350~650 ℃。

图1 TMF试验系统及试样示意图

表1 IN718高温合金物理参数[11]

图2 TMF试验中相关参数的变化曲线

在试样的标距表面沿轴向焊接3个K型热电偶，中间位置热电偶获得的温度信息作为试验系统的被控变量，两端热电偶测得的温度信息用于监测试样轴向的温度分布，确保轴向上的温差维持在规定范围内。感应加热电源输出功率是试验系统的控制变量，考虑到感应线圈电流是描述电磁场数学模型的关键变量，故采用柔性电流探头CP9060S测量感应线圈中的电流值、泰克TDS2012B示波器记录电流随时间的变化，电流频率为230 kHz，感应线圈电流随时间的变化如图2(b)所示。

2 感应加热过程的数学模型

在TMF试验中，感应加热是线圈中的交变电流产生交变磁场，在试样中产生相同频率的感应电流，从而加热试样的过程。试样位于感应线圈的中心位置，其中的电磁场和温度场近似认为呈轴对称分布，同时假设材料具有各向同性，将三维感应加热模型近似处理为二维轴对称模型，这样可以大大减少网格数量，提高计算速度。考虑到感应加热过程漏磁的影响，其计算区域需扩大至试样周围部分空气区域，选取计算区域如图3所示。感应加热过程数学模型包括描述电磁场和温度场的微分方程[12−13]。

图3 感应加热计算区域

2.1 电磁场数学模型

电磁感应过程中的电磁场规律可以用麦克斯韦方程组描述：

式中：为电流密度，A/m2；为电导率，S/m；为矢量磁位；为时间，s；为哈密顿算子；(是标量电位)；为磁导率(IN718是非铁磁性材料，=1)。

2.2 温度场数学模型

感应加热中温度场的数学模型为

2.3 边界条件

近似认为在空气域边界上的矢量磁位为零。试样表面单位面积上的热量损失为

式中：为表面的单位法向量；c为表面传热系数，W/(m2∙K)；s为试样表面温度，K；a为环境温度，K；为表面发射率；为斯特藩−玻尔兹曼常数，= 5.67×10−8W/(m2∙K4)；为综合传热系数，W/(m2∙K)。

其中，综合传热系数是TMF试验温度场数值模拟中的关键参数。一方面对试样进行感应加热，另一方面采用气体对试样表面进行冷却，使得试样的温度满足TMF试验的要求。在TMF试验的温度循环范围内，气体流量越大，综合传热系数越大。气体流量和风机电压是正相关的关系，所以，可由风机电压的大小预测综合传热系数的值。本文作者根据求解导热逆问题[14]的研究思路，采用迭代算法[15]计算综合传热系数，其计算流程如图4所示。风机电压和综合传热系数计算结果如图5所示，其中为设定的误差值。

图4 综合传热系数计算流程图

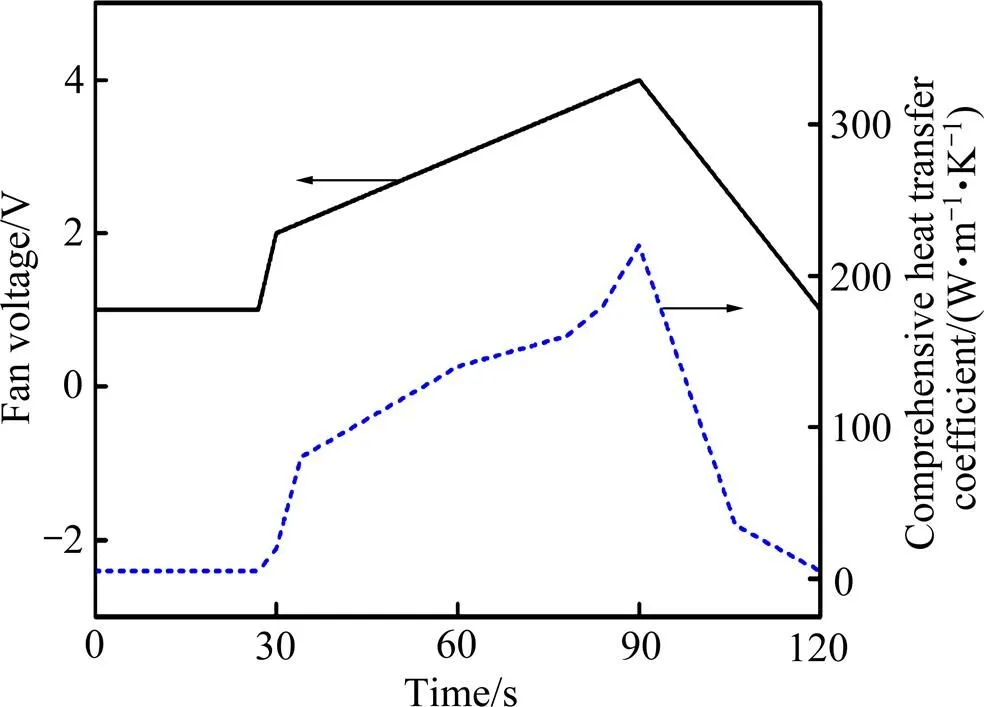
图5 风机电压和综合传热系数的变化曲线

3 结果与分析

为了便于分析试样温度场的变化规律和晶粒的长大情况，将试样横截面上中心、半径方向中点以及表面点分别设为c、m和s，对应的温度分别为c、m和s。

3.1 温度场

3.1.1 试样径向上的温度分布

电磁感应产生的热量主要集中在试样外侧较薄的一层厚度中，其透入深度[16]为

本模拟中试样的透入深度为0.011 mm。当冷却气体流量较小、试样透入深度内温度高于内部温度时，集中在试样外侧的热量一部分被冷却气体带走，另一部分向试样中心传递；当冷却气体流量较大、试样透入深度内温度低于内部温度时，试样内部的热量在热传导的作用下向表面传递，同时试样表面和冷却气体进行热量交换。

在一个循环周期中，试样的初始温度为500 ℃，不同时刻径向上的温度分布如图6所示。在31 s时，试样进入冷却降温阶段，感应电流由257 A降低至167 A，风机电压增大，试样表面综合传热系数增加，表面热损失增加，径向上的最高温度出现在m点和s点之间，如图6(a)所示。在60 s时，风机电压继续增大，试样表面温度降低，其内部的热量向表面传递，因此径向上的温度呈现由试样中心至表面逐渐降低的趋势，如图6(b)所示。

图6 不同时刻试样径向温度分布

3.1.2 试样径向温差随时间的变化

考虑到试样径向温差较小，最大温差约为5 ℃，本模拟中仅给出一个循环周期内两点之间的温差随时间的变化情况，如图7所示。由图7可知：在0~30 s内，试样被加热，其表面温度从500 ℃升高到650 ℃。循环初期，冷却气体流量较小，从试样表面带走的热量较少，感应线圈中的电流较大，试样温度主要受感应加热的影响。在集肤效应和热传导[17]的作用下，在考察的3点中试样表面温度最高，比中心温度高约 1.5 ℃，半径方向中点温度比中心温度高约0.6 ℃；在30~90 s内，试样被冷却，其表面温度从650 ℃降低到350 ℃。在30 s之后，电流突然减小，而冷却气体流量增大，从试样表面带走的热量增加，试样的温度在感应加热和气体冷却的共同作用下逐渐降低。在40 s之后，试样径向上温度呈现中心向表面逐渐降低的趋势，各点之间的温差趋于稳定，径向表面与中心两点之间的温差达到最大，其值为5 ℃左右；在90~120 s内，试样被加热，其表面温度从350 ℃升高到500 ℃。在90 s之后，电流突然增大，而冷却气体流量减小，由试样表面带走的热量减小，试样温度逐渐升高。循环后期，试样径向上各点温差趋于稳定，并与循环初期的温差基本保持一致。

图7 一个周期内不同点的温差变化曲线

本试验中试样达到的最大温度max=923 K，根据ASTM标准，试样径向上的最大温度差应小于最大温度的1%，即9.23 K。通过对试样温度场的模拟，径向上的最大温差在5 K左右，满足ASTM标准要求。

3.2 晶粒尺寸分析

本模拟中取两根相同尺寸的IN718合金试样分别进行LCF和TMF试验。LCF试验中试样温度恒定在650 ℃，其余参数和TMF试验设置相同。对c、m和s3个点做电子背散射衍射(EBSD)分析，在每个点附近采集3次数据，统计得到平均晶粒尺寸(AGS)。以s点为例，图8所示为其试验前后的晶粒尺寸分布图。不同条件下试样径向各点的AGS及增长幅度如表2所示。

对试样初始AGS进行分析，发现3个监测点的AGS在13.58~14.11 μm之间，最大差值小于4%，可认为所选试样的金相组织是均匀的。在LCF试验中，试样温度均匀一致，经过734次机械循环发生断裂，各点的AGS同样有所增长，其增长幅度基本相同，具体数值为15.80%~16.65%，表明晶粒生长规律基本一致；而在TMF试验中，试样经过201次热机械循环发生断裂，虽然各点的AGS都有所增长，但是中心位置的增长幅度为16.94%，与LCF试样的增长幅度相近；而表面位置的AGS仅增长5.03%，小于中心位置的1/3。不难看出，由于试样径向晶粒尺寸增长幅度的不均匀，使得合金材料的疲劳寿命显著降低。产生这种现象的原因在于：试样上加载循环热载荷时，其径向的温度梯度变化相差较大。由图7可以计算出：中心位置的径向温度梯度为−178~106 ℃/m，表面位置径向温度梯度为−602~154 ℃/m(考虑到集肤效应，该位置的温度梯度变化更大)。

图8 基于EBSD的晶粒尺寸分布图

表2 不同条件下试样径向各点的AGS及增长幅度

4 结论

1) 基于试验数据，采用迭代算法获得IN718合金在热机械疲劳试验中的综合传热系数和风机电压随时间变化的关系曲线。

2) 试样径向温度分布不均匀，在升温阶段，径向温差较小，表面温度大于中心温度；在降温阶段，径向温差较大，中心温度大于表面温度，其最大温差为5 K左右，满足ASTM标准要求。

3) LCF试样径向上不同点的AGS均有所增长且增长幅度基本相同，晶粒生长规律一致；TMF试样径向上的晶粒尺寸分布不均匀，中心位置的AGS增长幅度为16.94%，表面位置的AGS增长幅度则为5.03%。

[1] 唐中杰, 郭铁明, 付 迎, 惠 枝, 韩昌松. 镍基高温合金的研究现状与发展前景[J]. 金属世界, 2014, 26(1): 36−40. TANG Zhong-jie, GUO Tie-ming, FU Ying, HUI Zhi, HAN Chang-song. Research present situation and the development prospect of nickel-based superalloy[J]. Metal World, 2014, 26(1): 36−40.

[2] 黄志伟, 袁福河, 王中光, 朱世杰, 王富岗. M38镍基高温合金高温低周疲劳性能及断裂机制[J]. 金属学报, 2007, 43(10): 1025−1030. HUANG Zhi-wei, YUAN Fu-he, WANG Zhong-guang, ZHU Shi-jie, WANG Fu-gang. Low cycle fatigue properties and fracture mechanisms of M38 nickel base superalloy at high temperature[J]. Acta Metallurgica Sinica, 2007, 43(10): 1025−1030.

[3] MURAKAMI Y, FERDOUS M S, MAKABE C. Low cycle fatigue damage and critical crack length affecting loss of fracture ductility[J]. International Journal of Fatigue, 2016, 82(1): 89−97.

[4] KABIR S M H, YEO T I. Influence of temperature on a low-cycle fatigue behavior of a ferritic stainless steel[J]. Journal of Mechanical Science & Technology, 2014, 28(7): 2595−2607.

[5] 王媛媛, 陈立佳, 王宝森. 温度对625镍基高温合金焊接接头低周疲劳行为的影响[J]. 金属学报, 2014, 50(12): 1485−1490. WANG Yuan-yuan, CHEN Li-jia, WANG Bao-sen,Influence of temperature on low-cycle fatigue behavior of inconel 625 nickel-based superalloy welding joint[J]. Acta Metallurgica Sinica, 2014, 50(12): 1485−1490.

[6] 徐 涛, 高行山, 温志勋, 岳珠峰. 镍基单晶高温合金热机械疲劳本构模型研究[J]. 稀有金属材料与工程, 2015, 44(1): 108−112. XU Tao, GAO Hang-shan, WEN Zhi-xun, YUE Zhu-feng. Thermo-mechanical fatigue constitutive model for nickel-based single crystal superalloys[J]. Rare Metal Materials and Engineering, 2015, 44(1): 108−112.

[7] REDDY G V P, NAGESHA A, SANDHYA R, SANKARAN S, MATHEW M D, RAO K B S. Thermomechanical and isothermal fatigue behavior of 316LN stainless steel with varying nitrogen content[J].Metallurgical and Materials Transactions A, 2015, 46(2): 695−707.

[8] 王留兵. Z2CND18.12N奥氏体不锈钢低周疲劳及热机疲劳性能研究[D]. 天津: 天津大学, 2010: 27−61. WANG Liu-bing. A study of low cycle and thermomechanical fatigue behavior of Z2CND18.12N autenitic stainless steel[D]. Tianjin: Tianjin University, 2010: 27−61.

[9] 张国栋, 刘绍伦, 何玉怀, 苏 彬, 汪武祥, 杨治国. 粉末冶金盘材料FGH95热机械疲劳寿命预测[J]. 失效分析与预防, 2008, 3(1): 54−58. ZHANG Guo-dong, LIU Shao-lun, HE Yu-huai, SU Bin, WANG Wu-xiang, YANG Zhi-guo.Life prediction of thermomechanical fatigue in PM superalloy FGH95[J]. Failure Analysis and Prevention, 2008, 3(1): 54−58.

[10] ASTM E606/E606M−12. Standard test method for strain- controlled fatigue testing[S].

[11] 中国金属学会高温材料分会. 中国高温合金手册[M]. 北京: 中国质检出版社, 2012: 689−691.High Temperature Materials Branch of China Metal Institute. China high temperature alloy handbook[M]. Beijing: The Quality of China Publishing House, 2012: 689−691.

[12] KRANJC M, ZUPANIC A, MIKLAVCIC D, JARM T. Numerical analysis and thermographic investigation of induction heating[J]. International Journal of Heat and Mass Transfer, 2010, 53(17): 3585−3591.

[13] JAKUBOVIČOVÁ L, ANDREJ G, PETER K, MILAN S. Optimization of the induction heating process in order to achieve uniform surface temperature[J]. Procedia Engineering, 2016, 136(12): 125−131.

[14] PHILIPPE L M, TAHAR L, EUGÈNE A. Estimations of a 2D convection heat transfer coefficient during a metallurgical “Jominy end-quench” test: comparison between two methods and experimental validation[J]. Inverse Problems in Science & Engineering, 2004, 12(6): 595−617.

[15] 陈艳华, 张振迎, 景宝国. 试算法在多维非稳态导热问题中的应用[J]. 建筑节能, 2010, 38(1): 68−70. CHEN Yan-hua, ZHANG Zhen-ying, JING Bao-guo. Trial algorithm applied on multi-dimensional transient heat conduction[J]. Building Energy Efficiency, 2010, 38(1): 68−70.

[16] 叶 辉, 樊志新. 基于MATLAB钢丝感应加热模型及其温度场特性的研究[J]. 工业加热, 2005, 34(3): 11−14. YE Hui, FAN Zhi-xin. Research on the model of steel wire induction heating and its temperature field characteristic based on MATLAB[J]. Industrial Heating, 2005, 34(3): 11−14.

[17] HAN Yi, WEN Huai-yu, YU En-lin. Study on electromagnetic heating process of heavy-duty sprockets with circular coils and profile coils[J]. Applied Thermal Engineering, 2016, 100: 861−868.

Numerical simulation of transient temperature field during thermomechanical fatigue of IN718 alloy

CHEN Ji-guang1, 2, DENG Wen-kai3, 4, ZHOU Ping1, 2, JIANG Liang3, 4

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;2.Hunan Key Laboratory of Energy Conservation in Process Industry, Central South University, Changsha 410083, China;3. State Key Laboratory for Powder Metallurgy, Central South University, Changsha 410083, China; 4. Powder Metallurgy Research Institute, Central South University, Changsha 410083, China)

A mathematic model describing the induction heating process of IN718 superalloy was developed by coupling the electromagnetic field with the temperature based on the thermomechanical fatigue (TMF) test. The transient temperature fields of the specimen under cyclic heating condition were simulated. After the fatigue test, the grain size of the specimen was measured by electron backscattered diffractometry and the data were analyzed. The results indicate that the comprehensive heat transfer coefficient increases with the increase of the fan voltage. The temperature gradient in the radial direction of the specimen changes with time and the maximum of temperature difference is about 5℃, which meets the requirements of the test standard of TMF. The grain sizes of specimen in the radial direction increase at almost the same rate after the low cycle fatiguetest. However, the grain sizes of specimen in the radial direction distribute unevenly after the thermomechanical fatigue test, meanwhile the average grain size at the center and the surface increases by 16.94% and 5.3%, respectively.

supper alloy; thermomechanical fatigue; induction heating; temperature gradient; grain size

(编辑 龙怀中)

Project(2012AA03A514) supported by the National High Research Development Program of China; Project(61621062) supported by the Foundation for Innovative Research Groups of the National Natural Science Foundation of China

2016-05-30; Accepted date:2016-07-01

ZHOU Ping; Tel: +86-13975804856; E-mail: zhoup@csu.edu.cn

1004-0609(2017)-02-0265-07

TG156.1；TB115

A

国家高技术研究发展计划资助项目(2012AA03A514)；国家自然科学基金创新群体资助项目(61621062)

2016-05-30；

2016-07-01

周 萍，教授，博士；电话：13975804856；E-mail: zhoup@csu.edu.cn