周期性压力作用下单层幂律流底泥流场分布
刘洁,白玉川
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
周期性压力作用下单层幂律流底泥流场分布
刘洁,白玉川
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
基于欧拉坐标系统,对河口底泥流场分布进行了理论研究。泥波由作用在其表面的周期性压力驱动,底泥的流变特性由幂律流流变模型描述,根据浅水波和小变形假设,采用摄动分析展开到一阶得到运动方程,并且用数值迭代法求解非线性微分方程。根据数值计算结果,分析幂律流流动指数和外加周期性压力载荷对泥波流场分布和表面波高的影响。
底泥;幂律流模型;周期性压力;流场;波高
在我国长长的海岸线上淤泥质海岸线超过4 000 km。淤泥质海岸多地势平坦,是多种鱼类、贝类等生物以及藻类植物赖以生存的场所(刘晓收等,2014),是海洋湿地生态的重要组成部分;而各河口淤泥质海岸又存在不同程度的泥沙淤积问题(闫龙浩等,2010);加之深水航道的建设,使得河口淤泥质粘性泥沙的研究遇到新的挑战。由于受到水流、波浪和潮汐等多种因素影响,河口处的水动力环境异常复杂。其中,波浪与底泥之间的相互作用引起的泥波流场分布变化和波浪衰减受到学者的广泛关注。
研究波浪与底泥之间的相互作用时,上层流体和下层淤泥质底泥的流变特性一般由不同的流变模型描述。最早,Grade(1958)将上层水体假设为理想流体,下层底泥假设为粘性流体,建立了浅水条件下的两层流体模型;Dalrymple等(1978)考虑了上层水体的粘性,将上下两层都假设为粘性流体,建立起两层互不掺混的粘性流体模型;Ng(2004)根据边界层理论,将波浪与底泥均假设为粘性流体进行了研究;Ng(2004)还采用一种幂律流流变模型对底泥进行描述。另外一些研究考虑了底泥的固体特性,将底泥假设为粘弹性模型(赵子丹等1997;Ng,2002;牛小静等,2008)或者粘塑性模型(Becker et al,2000;Zhang,2006;Xia,2010;Xia,2011)。此外,还有一些研究同时考虑了底泥具有弹塑性,用粘弹塑性模型(牛小静等,2008)描述底泥的流变性质。
海岸床面底泥具有非牛顿流体特性,表现出典型的剪切稀化性质,即粘度随着剪切率的增大而减小。而底泥的这种性质可以由宾汉塑性体模型很好的描述,所以应用最为广泛。但是在理论研究中,瞬态理论很难确定宾汉塑性体模型的屈服位置,必须作为问题的一部分在计算中求解。因此,本文采用一种更加方便实用的流变模型,即幂律流模型。通过对天津海河口淤泥(白玉川等,2011)和连云港徐圩试挖槽浮泥(白玉川等,2011)的流变试验研究,发现幂律流模型可以很好地描述底泥的非线性流变特性,尤其是在低剪切率时(5-50s-1)。
本文在考虑淤泥质底泥非线性特性的基础上建立理论模型,对幂律流泥流的泥波流场分布进行初步研究。不同于传统的两层或者多层模型,为了简化数学模型,本文假设只有单层高浓度的淤泥存在;为了反映波浪与淤泥质底泥之间的相互作用,直接在淤泥质泥流表面作用周期性压力,类似的假设在Becker等(2001)研究波浪与底泥之间的相互作用中被采用。
1 理论模型与方法
1.1基本假设与公式
假设在水平的刚性床面上存在一层均匀的底泥,深度为h。底泥为不可压缩的各向同性体,密度为ρ,且沿x轴方向无限长,高浓度泥流用幂律流流变模型描述。为驱使底泥运动,外加压力直接作用在泥层表面,其形式为时间和空间的周期性函数,表达式类似行进波:P=Pscos(kx-σt);其中,Ps为压力幅值,k为波数,σ为角频率。泥波沿x轴的正方向传播,淤泥层底部固定在z=-h处;表面位置由η=z(x,0,t)表示,如图1所示。
x-z平面内的运动方程包括连续性方程、水平方向和垂直方向的动量方程


图1 泥波传播几何示意图

其中,u和w分别为沿x方向的水平速度和沿z方向的垂直速度,g为重力加速度。
如前所述,中国大多数河口海岸淤泥质底泥的流变特性可以由幂律流模型描述,而幂律流的流变关系(Ng,2004;白玉川等,2011)可以表示为
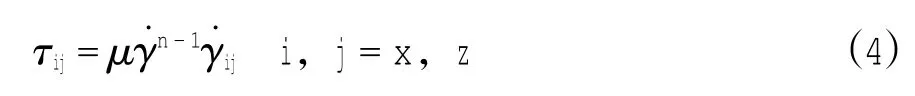

γ˙为剪切应力幅值,大小为

所以,各应力分量与剪切应力幅值可以表示成
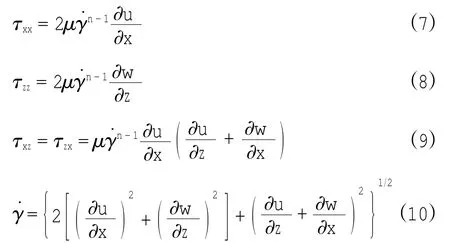
为了使方程完整,需要边界条件。首先,引入切应力T和正应力N表达式
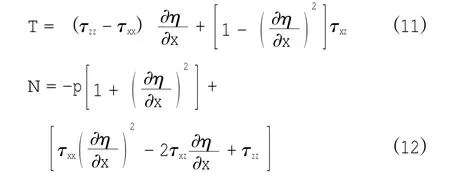
自由表面(z=0)处的动力学边界条件包括:切应力T为0,而正应力N等于外加压力载荷
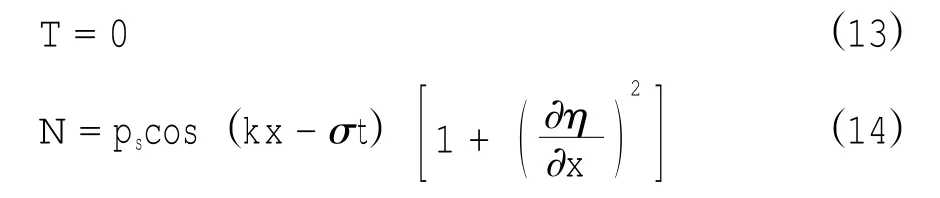
自由表面(z=0)处的运动学边界条件为:法向速度为零

底部(z=-h)边界条件为水平速度和垂直速度均为零

1.2无量纲化
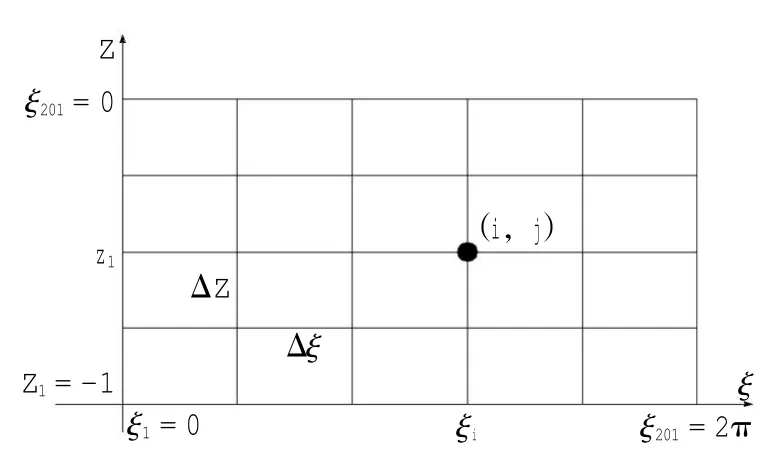
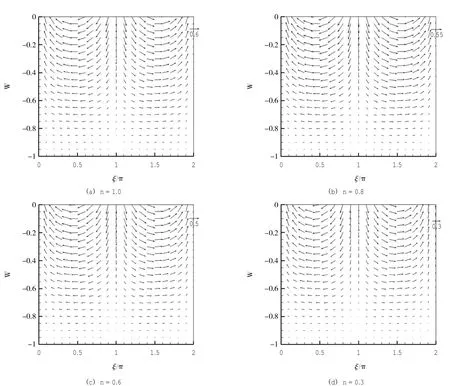
本文的一个重要假设是泥层厚度h远小于波长L,即h< 其中,Fr为弗劳德数;λ2为Stoke’s边界层厚度的平方与泥流厚度h的平方之比。 应力分量和剪切应力幅值的无量纲形式为 将式(33)带入无量纲运动方程式(19)-(21)和边界条件式(28)-(32),取其中一阶变量,就得到一阶问题的运动方程和边界条件。 一阶问题的连续性方程和动量方程分别为 其中,剪切分量 泥面波位移为 将式(37)和(43)带入式(35),得到如下一阶问题的控制方程 很显然,控制方程(45)为非线性微分方程,只有当流动指数n=1.0时,可以得到解析解。所以采用数值迭代法求解式(45),求解为范围0≤ 首先,式(45)可以写成如下隐式迭代格式 其中,uk表示第k步迭代,为已知量。uk+1为第k+1步迭代,为待求解未知量。 在网格结点(i,j)处,各变量的一阶和二阶中心差分格式为 将式(48)带入式(47),得到一阶控制方程的离散形式 图2 网格剖分示意图 自由表面(i=1,2,…,N,j=N)边界条件的离散形式为 底部床面(i=1,2,…,N,j=1)边界条件式的离散形式为 用数值迭代法求解时要输入以下几个参数:n,λ2,Fr和Ps。为了节省计算工作量,将流体为牛顿体(即n=1.0)时得到的u的解析解(Ng 2004)作为数值求解的初始值,求解得到n=0.9时的u值;并将n=0.9的解作为求解n=0.8时u的初值。以此类推,求解得到n=0.7、0.6、…、0.3时的数值解。当两次迭代之间的最大差值的绝对值差值小于10-4时,数值计算结束。文中其他参数值的设置分别为:λ2=Fr=1.0、Ps=1.0和Ps=2.0。为验证程序代码的正确性,对比n=1.0时的数值计算结果和假设流体为牛顿体时求解得到的解析解结果,如图3所示。 由图3可知,n=1.0时的数值解的流场分布与流体为牛顿流体时解析解的流场分布一致,从而证明了本文程序代码的正确性。当流体为牛顿体时,二维流场为简单简谐运动,水平速度u和垂向速度w为相位ξ的简谐函数。在表面周期性压力作用下,一个周期内的垂向速度w随压力梯度的变化遵循余弦函数变化:在相位ξ=0处,垂向速度w达到正的最大值,在相位ξ=π处达到负的最大值;而在相位ξ=π/2和3π/2处,垂向速度等于0。 图3 牛顿流体解析解结果二维流场矢量图 随幂律流流动指数n减小,二维流场分布如图4所示。由图可知,当载荷Ps=1.0,随着n值减小,泥流的非牛顿体特性越明显,虽然流场依然表现出周期性,但随着相位ξ变化,流场已经不再是简单的简弦变化;而且随幂律流流动指数减小的值增大,流场的变化越明显。此外,当幂律流流动指数n减小到一定值后,在ξ=0和π附近,由于作用力很小,出现流动静止状态,这种现象可以由剪切稀化现象解释。 图4 二维流场随幂律泥流流动指数变化的分布图 当载荷增加到Ps=2.0,随幂律流流动指数n减小,二维流场分布如图5所示。由图可知,当自由表面所施加的压力载荷从1.0增加到2.0时,二维流场在一个周期内仍然表现出周期性变化,而且最大速度值远大于Ps=1.0时。但是,随着流动指数nm减小,流场变化较Ps=1.0时并不显著。这是因为当外加载荷增大到一定值后,作用力对于泥波的影响大于泥流粘性对泥波运动的影响。同时,在ξ=0和π附近,由于作用力增大,流动静止现象也随之消失。 图6为一个周期内,波高随流动指数n变化的示意图。其中,图6(a)为Ps=1.0,图6(b)为Ps=2.0。由图可知,不同压力载荷作用下,波高均随流动指数n减小而减小。 当Ps等于1.0时,波高在ξ=π/2时达到正的最大值,即为波峰;而在ξ=3π/2时,波高到达负的最大值,即为波谷。随着流动指数越小,因为泥流的粘性越明显,驱动泥流运动所需得作用力就越大,图中表现为:n=1.0时的波高约为n=0.3时波高的两倍;然而当n从1.0减小到0.7时,波高变化并不明显,减小量小于1/5。 而当Ps增大到2.0时,流动指数n从1.0减小到0.3时,波高的减小幅度并不明显。这是因为当外加载荷增大到一定值后,作用力对于泥波运动的影响大于泥流粘性对运动的影响。此外,图6(a)更直观证明了图4中当n=0.3出现的流动静止现象,即在ξ=0和π附近流动出现间歇性停止。 本文基于欧拉坐标系统,介绍了一种摄动理论,初步研究了表面周期性压力作用下单层幂律流底泥的流场分布。主要得到以下结果: 图5 二维流场随幂律泥流流动指数变化的分布图 图6 波高随幂律流泥流流动指数变化示意图 当外加载荷等于1.0时,随幂律流流动指数n逐渐减小,二维流场虽然依然表现出周期性,但是已经不再是简单的简谐函数。而且,当流动指数减小到一定值时,会出现流动间歇性停止,这是因为河口底泥具有剪切稀化性质。 当外加载荷增大到2.0时,由于作用力对泥波运动的影响大于泥流粘性对其的影响,所以幂律流流动指数的减小对于二维流场的影响减弱,流动停止现象也随之消失。 然而,本文仅是对周期性载荷作用下泥流的流场分布进行了研究,这是研究波浪和底泥之间相互作用的第一步。后续工作希望基于两层波浪与底泥相互作用的数学模型,考虑二阶响应,研究幂律流流动指数和外加载荷对于流场和质量输移的影响。 Becker J M,Bercovici D,2000.Permanent bedforms in a theoretical model of wave-sea-bed interactions.Nonlinear Processes in Geophysics,201(7):31-35. Becker J M,Bercovici D,2001.Pattern formation on the interface of a two-layer fluid:bi-viscous lower layer.Wave Motion,34(1): 431-452. Dalrymple R A,Philip L F,1978.Waves over soft muds:a two layer model.Journal of Physical Oceanography,8(7):1121-1131. Gade H G,1958.Effects of a non-rigid impermeable bottom on plane surface waves in shallow water.Journal of Marine Research,16(3):61-82. Ng C O,2004.Mass transport in gravity waves revisited.Journal of Geophysical Research,109(12):1-13. Ng C O,2004.Mass transport in a layer of power-law fluid forced by periodic surface pressure.Wave Motion,39(3):241-259. Ng C O,Bai Y C,2002.Mass transport in a thin layer of Bi-Viscous mud under surface waves.China Ocean Engineering,16(4):423-436. Xia Y Z,Zhu K Q,2010.A study of wave attenuation over a Maxwell model of a muddy bottom.Wave Motion,47(8):601-615. Xia Y Z,Zhu K Q,2011.On a fractional-order Maxwell model of seabed mud and its effect to surface wave damping.Applied Mathematics and Mechanics,32(11):1357-1366. Zhang X Y,Ng C O,2006.Mud-wave interaction:a viscoelastic model.China Ocean Engineering,20(1):15-26. 刘晓收,赵瑞,华尔,等,2014.莱州湾夏季大型底栖动物群落结构特征及其与历史资料的比较.海洋通报,33(3):283-292. 牛小静,余锡平,2008.复杂粘弹性流体运动的数值计算方法.水动力学研究与进展A辑,23(3):331-337. 牛小静,余锡平,2008.泥质海床的粘弹性模型.清华大学学报(自然科学版),48(9) :1417-1421. 庞启秀,2011.浮泥形成和运动特性及其应对措施研究.天津大学.博士学位论文. 田琦,白玉川,2011.不同流变模型下的淤泥与波浪相互作用规律.天津大学学报,44(3):196-201. 闫龙浩,杨世伦,李鹏,等,2010.近期(2000-2008年)长江口南港河槽的冲淤变化——兼议外高桥新港区岸段强烈冲淤原因.海洋通报,29(4):378-384. 赵子丹,刘同利,1997.淤泥流变参数的确定.海洋通报,16(5):71-78. (本文编辑:袁泽轶) Flow field distribution in a layer of power-law muddy fluid forced by the periodic pressure LIU Jie,BAI Yu-chuan (State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China) Based on an Eulerian coordinate system, a theoretical research is presented for the flow field of muddy fluid which is forced by a periodic pressure on the free surface.The muddy fluid has a thin layer, which is described by a powerlaw model.By the assumption of shallowness and deformation, a perturbation analysis is carried out to the first order.The numerical iteration method is adopted to solve these non-linear equations.For the different fluid indices and pressure loads,both the flow field and wave height are examined. bed mud; power-law model; periodic pressure load; flow field; wave height P731.2 A 1001-6932(2017)01-0052-08 10.11840/j.issn.1001-6392.2017.01.007 2015-10-13; 2015-12-16 国家自然科学基金 (40376028);天津市应用基础研究计划(11JCYBJC03200)。 刘洁 (1986-),女,博士生,主要从事河口海岸淤泥特性和底泥质量输移研究。电子邮箱:liujie.mars@tju.edu.cn。 白玉川,男,教授。电子邮箱:ychbai@tju.edu.cn。

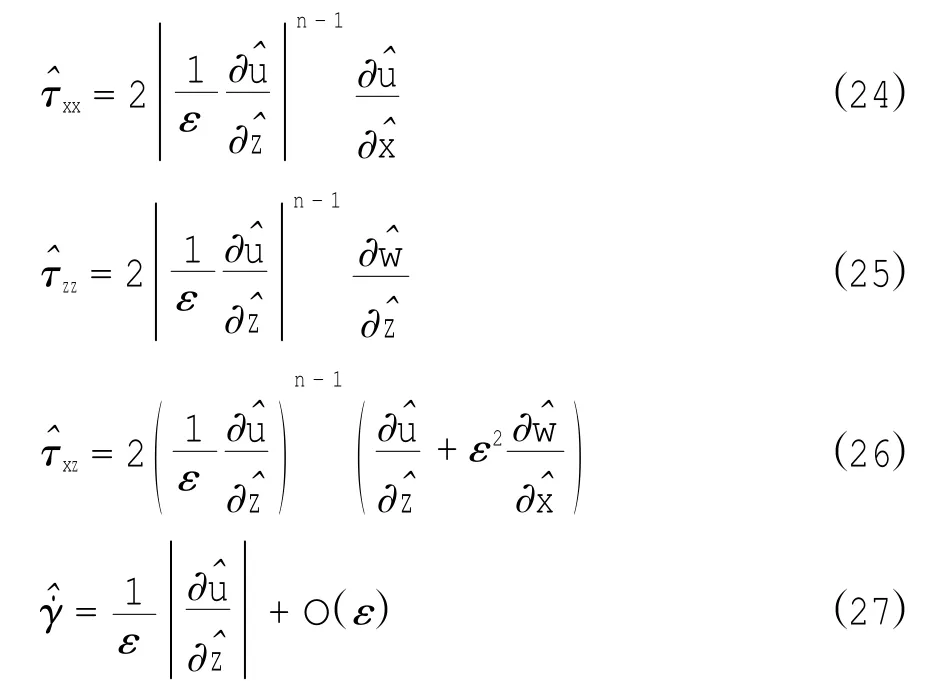


2 摄动分析






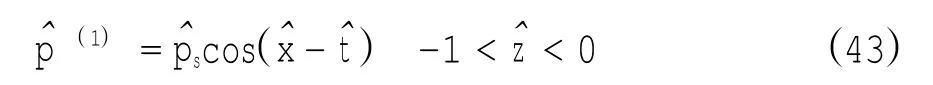
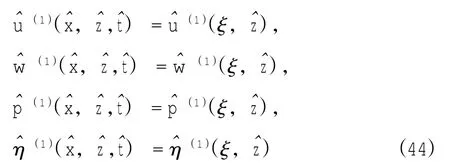


3 数值求解及结果分析
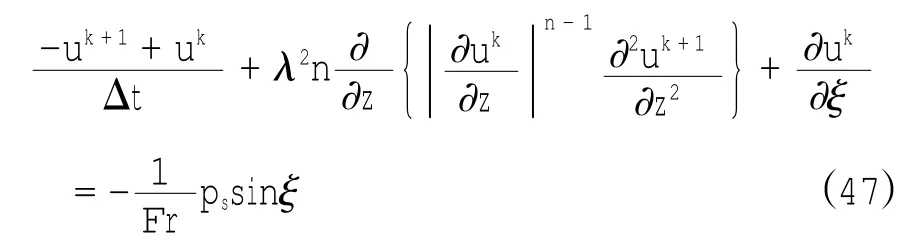





4 结论



