RP图及RQA分析法在滨海浅层地下水研究中的应用

路剑飞，甘华阳，徐穗珊

（1.国土资源部广州海洋地质调查局，广东 广州 510760；2.广州市海珠区气象局，广东 广州 510220）

RP图及RQA分析法在滨海浅层地下水研究中的应用

路剑飞1，甘华阳1，徐穗珊2

（1.国土资源部广州海洋地质调查局，广东 广州 510760；2.广州市海珠区气象局，广东 广州 510220）

以海南东北部滨海浅层地下水的逐时水位、电导率和地表气压监测数据为基础，利用RP图和RQA分析法对地下水系统的内部动力结构进行研究，分析ε和RR的取值对地下水系统比较结果的影响，并对台风过境引发的地下水系统内部动力结构的改变进行了相应的探讨。研究结果表明：（1）ε的取值对气压子系统的影响较小，但会明显放大或缩小水位和电导率子系统之间的差异性，尤其是电导率子系统，可能导致比较结果完全相反。（2）气压和水位子系统均具有漂移和破碎两种拓扑结构，电导率子系统则以破碎结构为主，部分兼具漂移结构。（3）当台风过境并产生影响时，地表气压出现明显的极小值，而地下水位则相应的出现极大值，RP图上表现为白色带状区域的出现。带状区域的边界可能暗示了台风影响的起止时间，而区域宽度则可能表征了台风的影响时长。此外，个别电导率子系统也相应出现了白色带状区域，很有可能意味着其也受到了过境台风的影响。（4）对于地下水系统而言，其层流态总是比确定性更为显著，系统的平均可预测长度则总是大于“特定状态”的受困时间，表明基于相邻轨道进行预测会获得更长的预见期。

海南；滨海浅层地下水；RP图；RQA

动力系统的演变分析，往往通过描述其相空间中轨道的演化特征加以实现。为了形象直观的展示动力系统的相空间轨道特征，绘制相图是必不可少的环节。但不足的是，相图最多仅能描述三维动力系统的相轨道，对于高维动力系统而言，相图仅能反映真实相轨道的二维或三维投影，无法给出其全貌。Recurrence Plots（简称RP图）应用的最初目的就是为了弥补相图的不足，通过二维图像的绘制，形象的展示高维系统的内部动力结构和时间演化特征。由于RP图是基于动力系统的递归性进行绘制的，而不同性质的动力系统其递归特征千差万别，因此可以根据RP图中典型的图案，对所研究的动力系统进行分类。此外，针对样本量不足和非平稳性等问题，RP图也具有很好的鲁棒性（Eckmann et al，1987；Marwan，2003a；Marwan et al，2007）。

根据RP图中图形结构的尺度大小，可相应的分为整体拓扑结构（Typology）和局部纹理结构（Texture） 两种。前者可以描述诸如同构（homogeneous）、周期（periodic）、漂移（drift）和破碎（disrupted）等内在的动力结构，从而形成对系统整体行为的认知（噪声、周期、自相关等）。后者则主要针对RP图中的单点、对角线、垂线/横线和弓形线等细微结构进行分析，结合具有定量分析能力的RQA（Recurrence Quantification Analysis）分析法，研究动力系统的小尺度变化特征（Marwan et al，2005）。

作为系统内部动力结构研究的重要工具，RP图和RQA分析法已广泛应用于生理学（Diaz et al，2001）、天体物理学（Kurths et al，1994）、生物学（Frontali et al，1999）、化学（Rustici et al，1999）、金融 （Belaire-Franch et al，2002）、地球科学（Marwan et al，2003b）等多个领域。然而，就目前而言，地下水领域，尤其是滨海浅层地下水方面的相关研究还十分匮乏。本文以中国地质调查局《华南西部滨海湿地地质调查和生态环境评价》项目为依托，利用海南东北部滨海地区三口地下水监测井（分别位于海口、文昌、万宁）获取的浅层地下水逐时水位、电导率及地表气压监测数据，借助RP图和RQA分析法对地下水系统（包含水位子系统、电导率子系统和气压子系统）的内部动力结构进行研究。同时，探讨地下水系统对过境台风的响应问题，以期从不同的角度获得新的认识。

1 区域概况与数据获取

海南岛位于我国最南端，地势以五指山、莺歌岭为中心，向四周逐级下降，由山地、丘陵、台地、平原构成环形层状地貌，梯级结构明显。根据含水层介质特征、地下水贮存条件和水力特征等因素综合判断，海南岛东北部滨海浅层地下水系统为潜水、微承压水和承压水组成的复式含水层系统，其中潜水多属于松散岩类孔隙潜水，而承压水则主要为多层砂粒孔隙承压水。潜水的补给来源主要为大气降水和灌溉水的渗入，侧向补给甚微；而承压水的天然补给来源则相对贫缺，仅第一、二层通过火山颈受上覆孔隙潜水补给（田开铭，1988；韩志明等，2009）。海南岛属热带季风气候，降雨主要来自台风和西南季风，由于携水气流多来自东部，加之中央山区的影响，因此降雨量由东往西锐减。东北部地区年均降雨量约为1 500～2 000 mm。降雨的来源也导致了海南岛雨季旱季分明，11月至次年5月为旱季，7个月的降雨量占全年雨量的10%～ 20%；雨季为5月至10月，集中了全年降雨量的80%～90%。因此，旱季多发生全岛性的旱灾，而雨季则多洪涝灾害，由此导致的地下潜水的水位变动也较为显著（陈飞星等，1998）。

为了研究海南岛东北部滨海浅层地下水动力及水质变化特征，在海口、文昌和万宁各建立一口地下水监测井（具体位置见图1），分别以QZ1、QZ2和QZ3表示。监测井选址的原则有2点：1）均为近岸高潮线附近靠陆地一侧；2）周围地势较为平坦且便于钻探。按照流域划分，三口监测井分属于南渡江流域、文教河流域和太阳河流域（何玉生等，2009），其中QZ1井位于南渡江河口区东侧。在监测井中各投放一台Solinst公司的M3001型电导率实时监测仪器（简称LTC）用于地下水水位及电导率的逐时监测，下放深度分别为20 m、16 m和20 m；井口地表位置各放置一台3001-M1.5型气压计用于记录地表气压变化。地下水监测井的钻探及监测均遵循《地下水环境监测技术规范》HJ/T 164-2004。文中所使用的监测数据的起止时间均为2013年7月12日11∶00-2013年11月14日10∶00，样本总量为3 000 h。

由监测井的水文地质柱状图判断（图略），QZ1井LTC下放深度刚好位于第一层承压含水层的底部，含水层顶部为具有弱透水性的粉质粘土层，厚度为3.4 m，距离地表14.9 m；含水层底部为不透水的粘土层，厚度为2.9 m，该层含水层厚度为1.7 m，含水层顶部至地面多为透水性良好的砂质含水层，中间夹杂有2层厚度均为0.8 m的淤泥层（透水性较差）。QZ2井的LTC下放深度位于珊瑚层底部（厚度为11.8 m），其上为透水性良好的中粗砂（厚度4.7 m）和粉细砂（厚度为0.3 m）。QZ3井的LTC下放深度则位于潜水含水层内，其上为透水性良好的粗砂（厚度17.3 m）和中砂（厚度为9.7 m）。由此可知，QZ1井LTC测量的为第一层承压含水层中地下水的电导率，该含水层与其上部潜水含水层的水体垂向交换极为缓慢，受降水补给的影响较弱。QZ2井和QZ3井测量的为潜水，均受降雨补给影响。

在监测时段内，有3场台风可能对调查区的监测数据产生影响，分别是Jebi（国际编号：1309）、Utor（国际编号：1311）和Krosa（国际编号：1329）。根据台风路径（图1），分别选择以下时段作为台风可能影响的时段进行研究：Jebi，8月2日14∶00-8月3日2∶00；Utor，8月14日2∶00-8月14日8∶00；Krosa，11月4日2∶00-11月4日14∶00。

图1 监测井站位图及台风路径图

2 气压、水位、电导率的统计分析

图2给出了监测时段内各监测井气压、水位、电导率的逐时变化曲线，气压、水位子图中的黑色虚线框表示台风过境时对应的监测时段，由于各监测井电导率在相应时段并没有明显的变化，因此并未标注。为了便于对比，QZ3井的水位比真实水位提高了4 m。由图2可知，三口监测井的气压和水位变化分别具有一致性，尤其是前者，为准同步变化。QZ3井的水位埋深明显较深，局部的水位变化与另外两口井的差异明显。就电导率而言，各监测井的电导率与气压、水位变化不具有显著的相关性。研究表明（陈娟等，2006；周鹏鹏等2014；付丛生等；2008）：在自然条件下，滨海浅层地下水系统受到潮汐的调制作用，按照驱动力的不同可具体分为固体潮、液体潮和气体潮3种，反映在潜水含水层内表现为潜水水位的变化，反映在承压含水层内则表现为承压水头的变化，这一变化相对于潮汐波动而言具有不对称性、振幅衰减及相位滞后等特征。此外，由于海水与地下水之间的连通性，对于潜水含水层和被海水切割的承压含水层而言，潮汐效应还会体现在水质变化上，而对于未被海水切割的承压含水层而言，其水质变化则仅体现地下水流场的变化特征。由于电导率反映了水中离子含量的多寡，与离子浓度、离子组成、水温、粘度等因素密切相关，而且具有测定随度快、程序简单、随机误差小且维护费用低廉等优点，因此在地下水水质的长周期监测中广泛使用，用以表征水质的长期变化特征。QZ1井监测的电导率为第一层承压含水层中地下水的电导率，与上部潜水含水层的垂向水体交换极为缓慢；QZ2井的地下水均来源于上层的潜水含水层，厚度仅为5 m，水体的垂向交换十分活跃，由于监测井位于近岸高潮线附近靠陆地一侧，潜水含水层部分水体在潮汐过程中与海水产生交换，因此地下水水质的潮汐效应显著；QZ3井监测的虽然也是潜水含水层的电导率，但由于仪器埋深较深（20 m），因此水体垂向运动相对QZ2井缓慢，电导率变化范围表明其位于咸水区。

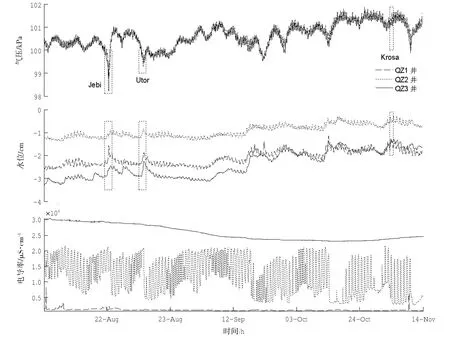
图2 气压、水位、电导率时序变化图

当有台风过境并对监测井处产生影响时（如Jebi和Utor），各监测井的地表气压出现了明显的极小值，水位则相应的出现极大值，表明当监测井处受到过境台风影响时，除了地表气压异常下降外，地下水位也会随之响应，异常抬升。而当台风Krosa过境时，各监测井的气压和水位并没有出现明显的极值，这很有可能是由于台风路径和强度的不同造成的（见表1）。相关资料和研究结果表明（顾申宜等，2012；Collins et al，2015）：台风过境引起的气压振荡式升降变化和摩擦会引起滨海浅层地下水水位的抖动现象，抖动周期为100～101 min；而台风过境带来的大量降水也会导致地下潜水面的显著抬升，尽管抬升的效果受到地表植被的制约作用。相比而言，各监测井的电导率则没有明显的变化，无法通过时序图直观判断出是否受到台风过境的影响。

表1 台风强度对比

3 气压、水位、电导率的RP图分析

RP图可以形象的描绘动力系统的整体拓扑结构，如同构（homogeneous）、周期（periodic）、漂移（drift）和破碎（disrupted）等。同构一般表征静止或自治系统，其RP图一般表现为大量的孤立点，不存在任何线状结构，这是由系统动力结构的剧烈变化导致的。周期和准周期系统则对应RP图中长且连续的平行于LOI的对角线结构，对角线被周期性式的结构分隔，分隔的时间步长即对应系统的特定周期。混沌系统也会产生对角线，但是长度要明显变短，对角线之间同样存在特定的垂直距离，但并不如周期运动一样规则和整齐。漂移（drift）是由于动力系统参数的缓慢变化导致的，如混沌系统，其RP图结构以主对角线（LOI）为中心分别向左上角和右下角褪变，表明所研究的过程是非平稳的或是处于状态转变的短暂阶段。动力系统的突变或极端事件的发生引发的非平稳性会导致RP图中产生大片的白色区域或波带（破碎），这也可能暗示系统动力状态的改变。RP图中由垂线和横线围成的黑色矩形区域表明某些状态一直持续或者随时间变化的十分缓慢（层流态），也有可能是所研究的过程中止于一个奇异点上，因此其动力特征陷于某种“暂停”的状态（王肖祎等，2014；Webber et al，2015）。

在针对单一时序进行研究时，为了有效的恢复所研究系统的内部动力结构，可以利用时间延迟的方法，通过计算系统的嵌入维m和嵌入滞时τ，重构系统的相空间，从而恢复系统的相轨道。当m≥2d+1时，可以认为重构的相轨道是可信的，其中d为吸引子维数（Packard et al，1980；Takens，1981）。本文分别采用 FNN法 （Kennel et al，1992）和互信息法（Roulston，1999）计算各系统的嵌入维m和嵌入滞时τ，为了下文叙述的方便，气压系统、水位系统和电导率系统分别用A、W和C表示，三口监测井则分别以1-3标识。由于井口气压和地下水水位之间存在一定的相关性（尤其是台风期间），而电导率是反映地下水水质的重要指标，因此本文将气压、水位和电导率系统分别作为一个完整的地下水系统的子系统进行研究。以A系统为例，A1-A3分别代表监测井QZ1-QZ3的地下水系统的气压子系统。表2给出了相应的计算结果，由表中可知：A子系统的差异性最小，嵌入维和嵌入滞时完全一致；C子系统的差异性最大，嵌入维和嵌入滞时完全不同。

表2 相空间参数计算表

恢复系统的空间动力结构后，要选取合适的ε值进行RP图的绘制，ε为定义递归状态的最小距离，其取值至关重要。ε过小将导致RP图中递归点数过少，不会形成有效的递归结构，从而无法获知系统的相关动力特征；而ε过大则会产生许多虚假的递归点，引起切向运动效应 （Tangential Motion），进而产生虚假的递归结构，导致对系统动力特征的误判。此外，系统中存在的噪声会扭曲RP图中的动力结构，因此适当较大的ε有助于去除噪声的影响。目前ε的取值标准并不唯一，有利用相空间直径的最大值或平均值作为判断依据的经验判别法 （Mindlin et al，1992；Koebbe et al，1992；Zbilut et al，1992），也有根据递归点密度（RR）进行判断的（Zbilut et al，2002）。当所研究的系统包含噪声，且噪声的标准差已知时，可以选择（Thiel et al，2002）。如果所研究的系统为周期（准周期）过程时，最优ε可以通过平行于LOI的对角线结构进行判定（Matassini et al，2002）。时间序列的标准差的倍数也常常作为ε的选择标准（钟季康等，2002；李新杰等，2013）。然而就目前而言，还没有适合所有系统的普适性的ε优选法则。

为了研究ε的取值对不同地下水系统比较结果的影响，绘制ε在0.1-2.5的变化区间内，A、W和C子系统的RR（Recurrence Rate）变化曲线（见图3），则ε对各子系统RR曲线的影响即可表征其对不同地下水系统比较结果的影响。此外，子系统对ε的不同响应特征，也可以部分反映出各子系统的内在差异。由图中可知：A子系统的RR曲线之间的差异性基本不随ε的变化而变化；而ε的不同取值会放大或缩小W和C子系统之间的差异性，尤其是C子系统，C1和C3曲线之间的多次交叉表明ε的取值可能影响比较结果的客观性。由于RR随ε的分布实际上反映了系统相空间中点的空间概率分布，由此可以推断，A子系统相空间中相点的分布最为一致，很可能具有相似的相轨道结构；C子系统的相轨道差异则最为显著。

图4给出了RR≈1%时各子系统的RP图，图中红色矩形区域即为3场台风的可能影响时段。由图中可知，A子系统的RP图几乎完全一致，表明A1-A3具有相似的递归结构，图中大片白色区域（波带）的存在及左上角和右下角递归结构的缺失暗示其非平稳性可能来源于系统自身的非平稳性和由于突变或极端事件引发的非平稳性两方面，因此A子系统同时具有漂移和破碎两种拓扑结构。与A相比，W子系统的递归结构虽然存在一定的相似性，如W1和W2，但差异也十分明显，如W2和W3。大块黑色矩形区域的存在表明W子系统的层流态十分显著，系统的某些特定状态可以保持相当长的一段时间或者改变的十分缓慢。与A类似，W子系统也同时具有漂移和破碎两种拓扑结构。C子系统的递归结构基本不具有相似性，尤其是C1-C2，C2-C3之间。与C2复杂的拓扑结构相比，C1和C3除了存在少数黑色矩形区域外，对角线结构（非LOI）和垂线/横线结构十分稀少，因此，C1和 C3仅具有破碎的拓扑结构，而C2则兼具漂移的拓扑结构。

图3 A、W和C子系统的RR vs.曲线

图4 A、W、C子系统的RP图（RR≈1%）

当台风过境时，受影响的地区往往表现为地表气压下降、风力加大、降雨的产生等多种气象要素的异常变化，因此准确判断台风作用的起止时段和影响时长需要综合多方面的影响。由A和W子系统的RP图可知，具有显著影响的Jebi和Utor台风过境时，其影响时段均对应气压、水位RP图上的白色条带状区域；而没有明显影响的Krosa台风过境时，则并未对应RP图中的特定结构。由于白色带状区域意味着系统动力结构的突变或极端事件的发生，因此区域边界可能暗示了台风影响的起止时间，而区域宽度则可能表征了台风的影响时长。此外，台风Jebi和Utor过境时，C2的RP图也对应出现了白色条带状区域，很可能意味着C2子系统也受到了台风作用的影响，这一结论是无法通过时序曲线直接获得的。

4 气压、水位、电导率的RQA分析

RQA分析法是基于RP图的定量分析方法，用于测量系统的复杂程度。与整体动力结构定性分类不同，RQA主要是基于RP图中递归点密度、对角线、垂线/水平线、弓形线等小尺度结构对所研究系统的典型动力特征（如可预测性（predictability）及laminarity（层状度）等）进行描述的一种定量方法。其中对角线结构的产生源于相轨道不同部分之间的平行演化（平行演化距离小于ε），这意味着轨道在不同的时间段访问了相空间中的同一区域，对角线的长度取决于平行演化的时间，平行演化的方向可以相同也可以相反。随机过程往往表现为较短的对角线结构，而确定性过程往往包含许多较长的对角线结构。垂线和横线则标志了一个状态不变或缓慢变化的时间长度，看起来似乎是这个状态被困住了一段时间，是层流态（间歇现象）的典型表现。对角线结构和垂线结构是RQA分析的基础。

本文在应用RQA分析法时，主要计算地下水系统的以下参量：RR、DET、L、LAM、TT，相关计算公式可参考文献（Webber et al，2015）。RR表示RP图中递归点的密度，反映系统的任意状态在未来重现的概率（Marwan et al，2009）。DET和L均为基于对角线结构的参量。DET也称为确定性，指形成对角线的递归点占所有递归点的比例，表征系统的确定性或平均可预测性，DET越大，系统的确定性或平均可预测程度越高。平均对角线长度L为两条相轨道相互接近（距离小于ε）的平均时间步长，也可解释为平均可预测时间。LAM和 TT则均为基于垂线结构的参量。LAM（Laminarity）类似DET，表示构成垂线的递归点占总递归点的比率，代表动力学系统的随机程度，用来说明递归图的复杂程度（孟庆芳等，2014）。垂线段平均长度TT（Trapping Time）用于衡量系统保持某一特定状态或某一特定状态被“困住”的平均时间。

图5给出了各子系统的RQA统计量随RR的变化曲线，其中基于对角线结构的参量（DET、L和Lmax）用x标记，基于垂线/横线结构的参量（LAM、TT和Vmax）用正方形标记；红色、绿色和蓝色分别对应QZ1井-QZ3井。由图中可知，A、W和C子系统均具有如下特征：1）不论RR取何值，均存在LAM>DET，即递归点组成垂线/横线的比率总是大于组成对角线的比率，意味着系统的层流态总是比确定性更为显著，尤其是A系统；2）不论RR取何值，均存在L>TT。虽然层流态比确定性更为显著，但基于相邻轨道的平均可预测长度总是大于“特定状态”的受困时间，表明基于相邻轨道进行预测会获得更长的预见期。

5 结论

本文以海南东北部滨海地区三口地下水监测井获取的浅层地下水逐时水位、电导率及地表气压监测数据为基础，借助RP图和RQA分析法对地下水系统（包含水位子系统、电导率子系统和气压子系统）的内部动力结构进行研究，分析对比了ε和RR的取值对地下水系统中各子系统比较结果的影响。此外，针对过境台风对地下水系统内部动力结构的改变进行相应的探讨，得出以下结论：

（1）ε的取值对气压子系统的影响较小，但会明显放大或缩小水位和电导率子系统之间的差异性，尤其是电导率子系统，可能导致比较结果完全相反。

（2）气压和水位子系统均具有漂移和破碎2种拓扑结构，电导率子系统则以破碎结构为主，部分兼具漂移结构。气压子系统的递归结构具有明显的一致性；水位子系统之间虽然存在一定的相似性，但差异也十分显著；电导率子系统则随监测井位置的不同表现出截然不同的递归特征。

图5 A、W、C子系统的RQA统计量变化曲线

（3）当台风过境并产生影响时，地表气压出现明显的极小值，而地下水位则相应的出现极大值，RP图上表现为白色带状区域的出现。由于白色带状区域意味着系统动力结构的突变或极端事件的发生，因此带状区域的边界可能暗示了台风影响的起止时间，而区域宽度则可能表征了台风的影响时长。此外，个别电导率子系统也相应出现了白色带状区域，很有可能意味着其也受到了过境台风的影响。

（4）对于地下水系统而言，其层流态总是比确定性更为显著，系统的平均可预测长度则总是大于“特定状态”的受困时间，表明基于相邻轨道进行预测会获得更长的预见期。

Belaire Franch J,Contreras D,2002.Recurrence plots in nonlinear time series analysis:free software.Journal of Statistical Software,7(9): 1-18.

Collins S V,Reinhardt E G,Werner C L,et al,2015.Regional response of the coastal aquifer to Hurricane Ingrid and sedimentation flux in the Yax Chen cave system(Ox Bel Ha)Yucatan,Mexico.Palaeogeography,Palaeoclimatology,Palaeoecology,438:226-238.

Diaz J O,Makikallio T H,Huikuri H V,et al,2001.Heart rate dynamics before the spontaneous onset of ventricular tachyarrhythmia in chagas heart disease.American Journal of Cardiology,87(9):1123-1125.

Eckmann J P,Kamphorst S O,Ruelle D,1987.Recurrence plots of dynamical systems.Europhysics Letters,4(9):973-977.

Frontali C,Pizzi E,1999.Similarity in oligonucleotide usage in introns and intergenic regions contributes to long-range correlation in the Caenorhabditis elegans genome.Gene,232(1):87-95.

Kennel M B,Brown R,Abarbanel H D I,1992.Determining embedding dimension for phase-space reconstruction using a geometrical construction.Phys.Rev.A,45(6):3 403-3 411.

Koebbe M,Mayer Kress G,Zbilut J,1992.Use of recurrence plots in the analysis of time-series data,in:M.Casdagli,S Eubank (Eds.), Proceedings ofSFI Studies in the Science of Complexity,Redwood City,Addison-Wesley,Reading,MA,XXI:361-378.

Kurths J,Schwarz U,Sonett C P,et al,1994.Testing nonlinearity in radiocarbon data.Nonlinear Processes in Geophysics,1(1):72-75.

Marwan N,2003a.Encounters with neighbours-current developments of concepts based on recurrence plots and their applications.University of Potsdam.

Marwan N,Kurths J,2005.Line structures in recurrence plots.Physics Letters A,2005,336(4-5):349-357.

Marwan N,Kurths J,2009.Comment on''Stochastic analysis of recurrence plots with applications to thedetection of deterministic signals''by Rohde et al.[Physica D 237 (2008)619-629].Physica D,238:1 711-1 715.

Marwan N,Romano M C,Thiel M,et al,2007.Recurrence plots for the analysis of complex systems.Physics Reports,438(5):237-329.

Marwan N,Trauth M H,Vuille M,et al,2003b.Comparing modern andPleistocene ENSO-like influences in NW Argentina using nonlinear time series analysis methods.Climate Dynamics,21(3-4):317-326.

Matassini L,Kantz H,Hołyst J,et al,2002.Optimizing of recurrence plots for noise reduction.Phys.Rev.E,65(2):1-6.

Mindlin G M,Gilmore R,1992.Topological analysis and synthesis of chaotic time series.Physica D,58(1-4):229-242.

Packard N H,Crutchfield J P,Farmer J D,et al,1980.Geometry from a Time Series.Physical Review Letters,45(9):712-716.

Roulston M S,1999.Estimating the errors on measured entropy and mutual information.Physica D-nonlinear Phenomena,d(3):285-294.

Rustici M,Caravati C,Petretto E,et al,1999.Transition Scenarios during the evolution of the Belousov-Zhabotinsky Reaction in an Unstirred Batch Reactor.Journal of Physical Chemistry A,103(33):6 564-6 570.

Takens F,1981.Detecting Strange Attractors in Turbulence.Lecture Notes in Mathematics.Springer,Berlin,898:366-381.

Thiel M,Romano M C,Kurths J,et al,2002.Influence of observational noise on the recurrence quantification analysis.Physica D,171 (3):138-152.

Webber C L,Jr,Marwan N,2015.Recurrence Quantification Analysis, Understanding Complex Systems.Springer International Publishing, Cham Switzerland.

Zbilut J P,Webber C L,Jr,1992.Embeddings and delays as derived from quantification of recurrence plots.Phys.Lett.A,171 (3-4):199-203.

Zbilut J P,Zaldívar Comenges J M,Strozzi F,2002.Recurrence quantification based Liapunov exponents for monitoring divergence inexperimental data.Phys.Lett.A,2002,297(3-4):173-181.

陈飞星，王华东，1998.海南岛水资源可持续发展对策.中国环境科学，18（增刊）：74-78.

陈娟，庄水英，李凌，2006.潮汐对地下水波动影响的数值模拟.水利学报，37（5）：630-633.

付丛生，陈建耀，曾松清，等，2008.滨海地区潮汐对地下水位变化影响的统计学分析.水利学报，39（12）：1 365-1 376.

顾申宜，张慧，解晓静，等，2012.海南井水位对热带气旋响应特征的分析.国际地震动态，6：278.

韩志明，廖传华，2009.海南岛地下潜水系统防污性能评价.地下水，31（1）：118-120.

何玉生，傅杨荣，王丰，等，2009.海南岛地表水的区域地球化学特征及其影响因素.地球与环境，37（2）：157-162.

李新杰，胡铁松，董秀明，2013.递归图法在径流时间序列非线性分析中的应用.武汉大学学报（工学版），46（1）：62-72.

孟庆芳，陈珊珊，陈月辉，等，2014.基于递归量化分析与支持向量机的癫痫脑电自动检测方法.物理学报，63（5）：050506-1 -050506-8.

田开铭，1988.对海口市地下水资源的初析.现代地质，2（2）：271-272.

王肖祎，仲兆平，王春华，2014.流化床内生物质石英砂双组分混合流动混沌递归分析.化工学报，65（3）：813-819.

钟季康，宋志怀，郝为强，2002.RQA在肌电分析中的应用.生物物理学报，18（2）：241-245.

周鹏鹏，李国敏，卢耀东，等，2014.承压水潮汐荷载效应研究进展.水文地质工程地质，41（4）：38-44.

（本文编辑:袁泽轶）

Applications of RPs and RQA in the shallow groundwater along the northeast coast of Hainan in China

LU Jian-Fei1,GAN Hua-Yang1,XU Sui-Shan2

（1.Guangzhou Marine Geological Survey,Guangzhou 510760,China;
2.Haizhu District Meteorological Bureau of Guangzhou City,Guangzhou 510220,China）

Based on hourly water table,conductivity and surface air pressure data from 3 groundwater monitoring wells located along the northeast coast of Hainan Province in China,RPs and RQA are employed to analyze the inner dynamical structures of groundwater systems.Impacts of different and RR values on RQA results of groundwater systems are analyzed in details.Furthermore,changes of dynamical structures in groundwater systems caused by the typhoon are considered.The results show that:1)ε has little impact on air pressure subsystems,but can truly expand or narrow the gaps in the water table or the conductivity subsystem,especially the latter one.2)Drift and disrupted structures are both contained in the air pressure and water table subsystems while not all conductivity subsystems have drifted structures.3)The impacts of typhoons passing by on the monitoring data will be reflected as white banding areas in the RPs of water table and air pressure,which shows boundaries of the area may infer the start-stop time point of the influence caused by typhoons,and the width of the area correspondingly represents the time interval of the influence.Additionally,RPs of some conductivity subsystem also has white banding area in the corresponding zone which may be considered as a hint of typhoon.4） For groundwater systems, laminarity is always greater than determinism,while the average prediction period based on adjacent trajectories is always longer than the average trapping time of certain status.

Hainan;coastal shallow groundwater;RPs;RQA

P345

A

1001-6932（2017）01-0043-09

10.11840/j.issn.1001-6392.2017.01.006

2015-09-11；

2016-01-07

中国地质调查局基金（1212010914020）。

路剑飞（1984-），男，博士，工程师，主要从事近海水文气象研究。电子邮箱：ppppwj1jf1@163.com。