基于MATLAB提取数字地图的电波传播问题研究

何 强，宋 铮，马斯敏

(1.电子工程学院,安徽 合肥 230037；2.西安通信学院，陕西 西安 710106)

基于MATLAB提取数字地图的电波传播问题研究

何 强1，宋 铮1，马斯敏2

(1.电子工程学院,安徽 合肥 230037；2.西安通信学院，陕西 西安 710106)

在抛物方程的基础上引入了地形高程剖面，预测了复杂地形条件下的电波传播特性。首先，基于MATLAB提取调用了数字地图，给出了其主要程序流程图以及提取调用的方法，之后采用插值方法增加了地形模型与实际地形剖面的契合度；其次，使用MATLAB的GUI功能设置了一个高程剖面系统，该系统能够提取地球上任意两点之间的地形高程剖面；最后，通过将高程剖面系统提取的地形高程剖面加入到抛物方程模型中进行计算，分析了在复杂地形环境下电波传播的特性。

数字地图；抛物方程；地形剖面；传输损耗

0 引 言

数字地图是高科技迅猛发展的一个产物，随着它的不断完善，现今的数字地图几乎能够涵盖所有地球上地形的特征信息。数字地图实际上就是将地球上的地理信息数字化，可以称之为数字地球。数字地图是以数字的形式记录和存储的地图，通过它能够十分方便地提取地形的地理位置信息。由于数字地图的时效性，使得其无论是在民用领域还是在军用领域都有十分重要的使用价值。

因为数字地图所能够带来的巨大效益，所以其提取应用的方法也广受人们关注[1]。本文提出了基于MATLAB提取数字地图的方法，通过MATLAB编程调用数字地图具有良好的实用性，工程价值较高。

预测电波在复杂地形环境下的传播特性是研究抛物方程法(简称PE)的一个重要方向。由于PE的计算十分复杂，而MATLAB编程相对于其它编程软件更为方便，并且数字地图也可以通过MATLAB[2]来提取，所以本文选用MATLAB进行编程计算。如果能够将抛物方程与数字地图相结合，把提取的地形高程剖面加入到抛物方程的计算当中，那么使用抛物方程法计算的效果更具有实用性。

本文使用MATLAB提取数字地图的地理信息并画出相应实际地形的高程剖面图，然后利用插值方法提高了计算模型的精度。通过计算自由空间中电波传输损耗和传播因子，分析了电波在自由空间中的传播特性，并将地形高程剖面加入到抛物方程法的计算当中，最后得到了电波传输损耗、传播因子以及它们的伪彩图。

1 抛物方程法的介绍

抛物方程法[3]是一种全波分析方法，它充分考虑了初始场、绕射效应、折射效应、上边界条件、阻抗边界条件以及不规则地形等因素对电波传播的影响，因而能够被广泛应用于分析电波传播的问题当中。其中，初始场可以通过对方向图函数进行傅里叶变换得到，上边界条件为窗函数，阻抗边界条件为Lenontovich边界条件。在胡绘斌的论文[4]中详细推导了直角坐标系、柱坐标系以及球坐标系下的抛物方程，本文用到的是球坐标系下的抛物方程。在球坐标系下讨论电波的传播过程中，设时谐场的时变因子为e-jωt，忽略波的后向传播，则可以得到宽角抛物方程(WAPE)(在胡绘斌的论文中给出了推导过程，由于篇幅有限在这里不作介绍)：

(1)

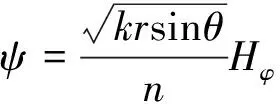
其中坐标转换的具体表达式：

(2)

式中：a为地球半径；h为距地表高度。

根据参考文献[5]，通过分布傅里叶变换(SSFT)算法推导上式得到：

(3)

从解的形式中可以知道SSFT是一种步进迭代算法，该算法受波长限制小，稳定度高，求解速度快。而分布傅里叶变换的核心是将折射项和绕射项相分开，可以单独对绕射项进行傅里叶变换运算。

(4)

LF=20lg|u(x,z)|+10lgx+10lg10λ

(5)

2 提取高程数据

2.1 地形数据

数字高程模型(DEM)是使用一组有序数列形式表示地面高程的一种实体地面模型，由于数字地图能够将山川、河流、海面及陆地的属性和地理位置信息表现出来，因此其能够在计算机中真实地反映地形情况。

本文中，数字地图的地形信息数据存储的格式为Grid型DEM-DTED，其高程数据是以网格的数据进行存储的。DTED存储格式是以左下角为起点，每一列为一个记录单元，并且经度、纬度以递增的方式存储高程值。在数字地图准备好了以后，MATLAB中DTED函数可以载入始末2点内的经度和纬度高程信息，并以二维数组形式储存。图1就是DTED的一个小文件，表达了经度从东经116°到117°，纬度从北纬30°到31°区域内的高程数据。

2.2 插值算法

通过数字地图，只需要知道任意2点的经纬度信息，就可以提取它们之间的地形高程剖面。图2是发射点(116.477 9°E，30.569 3°N)和接收点(116.437 1°E，30.610 2°N)之间的高程剖面，其高程剖面是由一个个离散点组成的，而特定点位的坐标信息是唯一的。在实际环境条件下，由于所考虑的地形是不固定的，所以在数字地图中提取的离散采样点的位置也是随机的。为了使PE中的每个步进都有相对应的离散点，也为了提高计算的精度，本文中引入内插法进行计算。

数字地图的数据信息是由很多个离散点组成的，相邻2点之间数据信息相近，关联性较大，而内插方法正是通过在相邻2点之间做连线，再根据这2点的高程数据信息可以求出连线上任意一点的高程数据。图3是它的原理分析图。

A(x1,y1),B(x2,y2),C(x3,y3)是数字地图中的存储数据，A和B两点之间连线上任意一点的坐标为D(x4,y4)，有：

(6)

变换上式可以得到：

(7)

所以只需要知道所求高程点的横坐标x4，就可以得到其纵坐标及高程信息。当实际计算时，x4表示的是某个步进的距离，它可以从MATLAB中获得。

2.3 地形剖面的提取

2.3.1 程序流程图

程序流程图如图4所示。

2.3.2 高程剖面系统

使用MATLAB中GUI[6]功能按照程序流程图4设计一个系统，如图5所示。该系统中有高程剖面[5]和传输路径高程2个模块。在高程剖面模块中有发射站和接收站位置按钮、收发站的经纬度信息以及传播距离(不输入，会自动算出)；传输路径高程模块在高程剖面模块输入地理位置数据后进行计算就可以自动输出。图6是输入数据后的界面。

该系统可以提取任意2点之间的地形剖面信息，输出图形的横坐标为距离(km)，纵坐标为高度(m)。该系统操作十分简单，只需要输入发射站和接收站的经纬度信息，然后点击发射站和接收站位置按钮则传播距离以及传输路径高程都会自动算出。

3 PE与数字地图相结合分析电波传播问题

3.1 地形模型的选取

根据实际地形的不同，许多学者提出了不同的地形模型，其中有地形遮蔽模型[7]、连续移位变换模型[8]、离散移位变换模型、宽角移位变换模型[9]等。而地形遮蔽模型最适合应用于数字地图的地形剖面中，故本文选用地形遮蔽模型。

该模型是由S.Ayasli和Newkirk等人提出的，其基本原理就是将复杂地形以阶梯化的形式来表示，如图7所示。

在分析电波传播时，只考虑垂直地形S1面上的场，并将S2面上的场设置为零，模型的地表下场都设置为零。采用地形遮蔽模型时，可以通过减小步进长度以提高其计算的精度。

图8是MATLAB提取数字地图中发射点(116.257 5°E，30.332 0°N)和接收点(116.555 9°E，30.185 8°N)之间的地形高程剖面。图9是通过地形遮蔽模型方式处理后的剖面图(设定的计算距离为31 km)，其中每个台阶的长度为1个步长。通过图8可以看出，该地形起伏变化较大，如果单使用地形遮蔽模型对该地形剖面进行计算的话则精度较低，因此可以减小步进长度和使用内插法提高其阶梯化的精度，图9是修正后的地形模型。

由图9可以看出，通过减小步进长度和使用内插法修正后的地形模型与原地形十分相近，所以计算的精度会得到有效提高。

3.2 计算实例

在标准大气条件下，发射天线架高为hr=120 m，电波的工作频率f=1 000 MHz，极化方式为垂直极化，地质为非常干燥地，εr=3，电导率为σ=0.000 1 S/m。选择图8中的发射点和接收点位置，但是将收发2点之间的地形设为光滑球面地，计算距离为31 km，设定的水平步长为100 m，接收天线架高以h1表示。使用离散混合傅里叶变换(DMFT)算法对抛物方程进行计算，得到的传播因子随

高度以及距离的变化曲线如图10(a)、(b)所示。

图10(a)为传播因子随高度变化图，从图中可以看出，随着接收天线高度的增加，传播因子的值在零点左右震荡且震荡不断变小，这是因为随着高度的增加地面反射波能量越来越小，所以其干涉效应逐渐减弱；图10(b)中传播因子也是围绕零点震荡，而近距离的震荡较远距离的震荡更加密集，这是因为距离越近波程差变化越大，距离越远波程差变化越小。

3.3 把高程剖面数据加入到抛物方程中

仍然选用图8的经纬度数据，但是引入实际的复杂地形,重新进行相应的PE分析计算，得到了反映电波传播特性的图11～图15。

从图11可知，在山峰后的山脚处传输损耗最大，并且山峰后的传输损耗明显大于山峰前的传输损耗。从伪彩图12中也可以看出山峰后的传输损耗大于传播前的传输损耗，对于电波在山峰后的传播而言，此山峰类似于尖劈。

图13计算的是传播因子随接收天线高度的变化情况，随着高度的增加传播因子逐渐变大。当接收天线的高度高于120 m时，传播因子在零值处震荡，说明此山峰的尖劈效应开始显现。图14反映了传播因子随距离的变化，从图中可以看出，山峰前的传播因子仍然体现了直接波和地面反射波的干涉效应，但是山峰的存在导致山后的传播因子明显变小。图15是传播因子的伪彩图。

4 结束语

首先，本文提出了使用MATLAB提取调用数字地图地形高程剖面的方法。该方法简单实用，易于操作，具有良好的实用价值；然后，通过调整步进长度和使用内插法提高了地形遮蔽模型与实际地形的契合度，从而提高了计算模型的精度；最后，将MATLAB提取的地形高程剖面加入到抛物方程的地形边界条件当中进行计算，分析了复杂地形环境下电波传播的特性。

[1] 白瑞杰，廖成，盛楠，张青洪.基于二维数字地图的电波传播问题仿真[J].强激光与粒子束,2014,26(7)：191-194.

[2] 陈天伟.应用MATLAB构造数字高程模型工具箱[J].桂林工学院学报，2003,23(4)：453-456.

[3] 马斯敏，宋铮，马恒民.基于FEKO/PE混合算法的近地线天线地波场求解[J].安徽.微波学报,2014,30(6):46-50.

[4] 胡绘斌,毛钧杰.预测复杂环境下电波传播特性的算法研究[D].西安.西安电子科技大学出版社,1995.

[5] 马斯敏，宋铮.基于抛物方程的地面电波传播特性分析[D].合肥：电子工程学院，2014.

[6] 罗华飞.MATLAB GUI设计学习手记[M].北京：航空航天大学出版社，2014.

[7] NEWKIRK M H.Recent advances in the tropospheric electromagnetic parabolic equation routine (TMPER) propagation model [C]//Battlespace Atmosph.Conf,1997:78-85.

[8] BARRIOSS A E.A terrain parabolic equation model for propagation in the troposphere[J].IEEE Transactions on Antennas and Propagation,1994,42(1):90- 98.

[9] DONOHUE D J.KUTTLER J R.Propagation modeling over terrain using the parabolic wave equation[J].IEEE Transactions on Antennas and Propagation,2000,48(2):260-277.

Study of Electric Wave Propagation Problems in Digital Map Extration Based on MATLAB

HE Qiang1，SONG Zheng1，MA Si-min2

(1．Electronic Engineering Institute of PLA，Hefei 230037，China; 2.Xi'an Communication Institute，Xi'an 710106，China)

This paper introduces the terrain elevation profile based on parabolic equation,forecasts the electric wave propagation characteristics under the complex terrain condition.This paper firstly extracts and calls the digital maps based on MATLAB,gives the main program flow chart and the extraction and call method,then uses interpolation to increase the consilience between terrain model and practical terrain profile;secondly uses GUI function of MATLAB to set an elevation profile system which can extract the terrain elevation profile between random two points on the earth;finally adds the terrain elevation profile extracted by elevation profile system into parabolic equation model and performs calculation,analyzes the characteristics of electric wave propagation in complex terrain environment.

digital map;parabolic equation;terrain profile;propagation loss

2016-03-03

TN011

A

CN32-1413(2017)01-0062-06

10.16426/j.cnki.jcdzdk.2017.01.014