PRS/IRS复合制导中时空对准方法研究
薛 鹏,董文锋
(空军预警学院,湖北 武汉 430019)
PRS/IRS复合制导中时空对准方法研究
薛 鹏,董文锋
(空军预警学院,湖北 武汉 430019)
针对被动雷达/红外(PR/IR)复合制导中2种传感器数据融合中时空对准的问题,提出了坐标变换的空间对准方法和最小二乘法曲线拟合的时间对准方法。Matlab仿真结果证明,该时空对准方法能将2种传感器通过不同采样周期得到的数据进行有效对准,实现了数据融合。
被动雷达/红外复合制导;时空对准;坐标变换;最小二乘法
0 引 言
随着科学技术的发展,传感器性能获得了很大的提高,各种面向复杂应用背景的多传感器系统大量涌现[1]。现代高科技战争中,通过单一传感器已经不能达到预期目的,为获得更佳作战效果,必须充分利用包括各种有源和无源探测器在内的多传感器,得到更多、更全面的观测数据。
分布在不同平台、不同类型和不同精度的传感器,由于安装的位置不同,测量速率的不同,如若处理不当,就不能发挥多传感器的优势,使数据的可用性大大降低,严重影响后续问题的解决。这就要求首先对来自多传感器的测量数据进行可靠的空间对准和时间对准。本文主要研究的是被动雷达和红外传感器的数据融合算法。
1 数据空间对准
所谓数据空间对准就是选择一个基准坐标系,把来自不同平台的多传感器数据都统一到该坐标系下[2]。利用空间坐标变换可以实现数据空间对准。目前,无论是在反辐射导弹(ARM)还是反辐射无人机(ARUAV)中,被动雷达和红外传感器都是分孔径设计安装(如图1所示),且两者有不同的量测坐标系。在实际应用当中,不仅要考虑利用坐标变换对传感器进行空间配准,也要考虑到系统本身的固有偏差。
1.1 系统固有偏差校正
量测系统本身就具有一定的误差,可以通过对位置已知的目标进行量测来完成各个传感器的校正工作。工作原理如图2所示,利用下式进行计算:
(1)
式中:rm、θm和φm为传感器量测到的目标距离、方位角和俯仰角;r、θ和φ分别为真实目标的距离、方位角和俯仰角;Δr、Δθ和Δφ为系统的固有偏差;εr、εθ和εφ为均值为零的高斯随机测量误差。
常用的方法是通过多次测量求平均值来达到减小误差的目的。由式(1)得到系统固有误差并多次测量,利用式(2)求平均,可以实现对系统的固有偏差的校正:
(2)
1.2 坐标变换
坐标变换包括空间坐标系的旋转和平移2种。空间坐标系的旋转不改变坐标轴的原点而改变坐标轴的指向;空间平移变换恰好与前者相反,不改变坐标轴的方向而只改变原点的位置。
空间坐标系的旋转就是将某一坐标系A中的矢量Q转换到另一坐标系B中,只需将矢量Q乘以坐标系之间的变换矩阵即可得到[3],即:
(3)
例如,将A坐标系绕OX轴旋转α角,得到B坐标系:
(4)
式中:RX[α]为转换矩阵。
同理可得到绕OY、OZ轴旋转β、γ角的转换矩阵RY[β]和RZ[γ],这样就可以得到矩阵A到B的转换矩阵RA→B=RX[α]·RY[β]·RZ[γ]。
不难证明,坐标变换矩阵RA→B满足如下的可逆和正交条件,即:
(5)
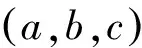
(6)
(7)
式(6)、式(7)就是坐标轴的平移公式。
1.3 仿真分析
在被动雷达/红外复合导引头中,两者处于同一个平台上,由于其本身特性和工程实现的原因,目前为止还无法做到共孔径安装,两者的空间对准可以利用上述空间旋转和空间平移相结合的方法进行计算,从而达到空间对准的目的[4]。
假设ARM或者ARUAV上安装的被动雷达导引头(PRS)和红外雷达导引头(IRS)经过一段时期的工作,采集到的数据如表1所示。

表 1 测量数据
图3显示的是红外导引头和被动雷达导引头在以各自为原点的坐标系中采集到数据和经坐标变换对准到同一坐标系中,简单加权融合之后的Matlab仿真结果。从图中可以看出:未经对准的单一导引头测得的数据变化幅度比较大,即测向稳定度不高;而经过空间对准,简单加权融合之后的结果要比单一导引头的数据变化幅度小,稳定度得到了显著的提高。这说明空间对准之后ARM或ARUAV的飞行轨迹更为平稳,有利于整个飞行过程中的控制,制导精度也会得到有效提高。
2 数据时间对准
数据时间对准就是在某一时间片段内,利用各种算法将各个传感器采集到的不同步测量数据同步到同一时刻下。
2.1 时间对准基本方法分析
时间对准的方法有很多,常用的有最小二乘准则和插值法。在被动雷达/红外复合导引头中,由于两者的采样速率是不相同的,就需要对不同步的测量数据进行时间对准。常用的时间对准方法有很多[5],比如内插(外推)法、拉格朗日插值法、牛顿插值法、三次样条插值法和最小二乘算法等。拉格朗日插值法比较繁琐,当插值点发生变化时,整个计算过程必须从头开始,计算量大,没有继承性,而且当插值点较多时,插值多项式的阶数可能会很高,数值可能会出现不稳定的情况,和真实值会有很大的偏差;牛顿插值法是对拉格朗日插值法的改进,克服了拉格朗日插值法的缺点,具有继承性,但是这2种算法都只适合于对插值精度要求不高的工作环境中(要求一阶光滑度);三次样条插值虽然计算简单且数值稳定度较高,但是其只能保证每个小段曲线在连接点处的光滑,并不能保证在整条曲线的区间都光滑。最小二乘曲线拟合不要求拟合出来的曲线经过每一个量测数值点,但是要保证满足误差平方和最小原则,这样就能使拟合曲线更接近于真实函数。通过实验证实:相同数据量的条件下,最小二乘算法的运算时间要比插值法的运算时间低一个数量级,实时性比较好。综合考虑到最小二乘曲线拟合法的优势,所以本文选择此法进行时间对准方法的研究论证。
2.2 最小二乘曲线拟合法
最小二乘法曲线拟合的基本理论[6]:
假设通过量测已经得到一组量测数据:(tk,Xk)(k=1,2,…,n),则可设待拟合函数近似于线性表达式为:
(8)
量测数据和拟合曲线的偏差为:
X(tk)-Xk=a·tk+b-Xk,k=1,2,…,n
(9)
偏差的平方和为:
(10)
由最小二乘原理知应当取合适的a和b使偏差的平方和F(a,b)达到最小,即F(a,b)对a和b分别求偏导数并令其为零,如下式:
(11)
解上式可以得到:
(12)
通过解上述方程组,求得a、b的取值,这样就可以得到拟合曲线的函数,从这条曲线可以读出该传感器在任意时刻的数据,也可以读出其他传感器在相同时刻对应的数据,这样就完成了多传感器数据的时间对准。
2.3 仿真分析
假设ARM或者ARUAV上安装的PRS和IRS的采样速率分别为0.1s和0.018s,为了保证拟合的精度,选择将高精度观测时间上的数据推算到低精度观测时间上的数据,即将IRS的数据对准到PRS。设定起始时间是0s,终止时间是0.1s,这样就可以得到2组分别由PRS和IRS采集到的俯仰角数据,如表1、表2所示。

表2 PRS测量数据

表3 IRS测量数据
如前文所述,对高观测时间精度的IRS数据进行仿真研究,仿真结果如图3和图4所示。
分析图3可以看出,拟合曲线和原始数据的拟合效果还是比较理想的,没有偏差特别大的情况出现;分析图4可以看出,每个数据的拟合结果误差都控制在0.01mrad以内,甚至更小。从图3给出的拟合多项式或者拟合曲线便可以得到PRS在0.1s的数据,这样就完成了从高观测时间精度到低观测时间精度的推算,解决了2种不同传感器之间时间
对准的问题。对方位角的计算拟合与俯仰角的计算拟合方法一致,此处不再赘述。对于仿真的结果,假设ARM或者ARUAV在攻击过程中的失控距离是800m,导引头跟踪时的视场宽度为±4°,如果在失控距离临界处的误差为1mrad,经计算可以得到武器落在地面的杀伤范围的圆心偏差约为0.8m,而现在一般的ARM和ARUAV杀伤半径至少都在15m以上,这个误差完全可以满足作战需求。
3 结束语
多传感器的时空对准是多传感器数据融合的基本前提[7]。本文利用空间变换和基于最小二乘法的曲线拟合方法,实现了不同安装位置(平台)和不同观测时间精度的多传感器的时空对准。仿真实验结果表明,该方法精度高,易实现,进一步提高了数据融合的可靠性。
[1] 何友,王国宏.多传感器信息融合及应用[M].北京:电子工业出版社,2010.
[2] 林华,玄兆林,刘忠.用于多传感器目标跟踪的数据时空对准方法[J].系统工程与电子技术,2004,26(6):833-835.
[3] 周颖,甘德云,许宝民.反辐射武器攻防对抗理论与试验[M].北京:电子工业出版社,2012.
[4] 潘自凯.被动雷达/红外复合导引头抗多点源诱偏技术研究[D].武汉:空军预警学院,2011.
[5] 曾绍标,熊洪允,毛允英.应用数学基础[M].天津:天津大学出版社,2004.
[6] 梁凯,潘泉.基于曲线拟合的多传感器时间对准方法研究[J].火力控制与指挥,2006,31(12):51-53.
[7] 何友,何修娟,关欣.雷达数据处理及应用[M].北京:电子工业出版社,2013.
Research into Time and Space Alignment Method in PRS/IRS Combined Guidance
XUE Peng,DONG Wen-feng
(Air Force Early Warning Academy,Wuhan 430019,China)
Aimed at the time and space alignment problem for data fusion of two kinds of sensors in passive radar/infrared (PR/IR) combined guidance,this paper puts forward the space alignment method based on coordinate transformation and the time alignment method based on least square curve fitting.The results of Matlab simulation demonstrates that the methods proposed can effectively align the data with different sampling periods obtained from two kinds of sensors,realizes the data fusion.
passive radar/infrared combined guidance;time and space alignment;coordinate transformation;least square method
2016-08-25
TN974
A
CN32-1413(2017)01-0043-04
10.16426/j.cnki.jcdzdk.2017.01.009

