基于CEL方法的ADS系统主容器抗震性能分析
刘鋆华,黄天璨,谭 平
(广州大学,广州 510405)
0 引言
ADS(Acceleration driven system)嬗变系统是一种可以降低废料辐射的新型核电技术,符合我国可持续性发展的先进技术需求。与传统的核电站相比,ADS嬗变系统体量大为缩小,其反应堆主容器没有巨型结构支撑体系,结构刚度远不如传统核电结构,存在着一定的抗震风险。为确保ADS嬗变系统在地震下的安全,需要进一步深入研究ADS系统的抗震性能。
国内外对于ADS嬗变系统的抗震性能研究目前尚处于起步阶段,尤其是对ADS系统的反应堆主容器在地震作用下的流固耦合效应研究。国内学者以往针对容器流固耦合效应的抗震性能研究主要集中在储油罐等大型罐体结构上[1-5],研究重点是储油罐可能发生的屈曲。而ADS的反应堆主容器体积相对较小,内部冷却剂为铅泌液体,液体密度大,达到10 470 kg/m3,与质量较轻的液体相比,其运动黏度也有很大的差异,在堆芯正常工作温度下其运动黏度达到了室温情况下水的2.5倍、甘油的2倍。当前国内对于ADS系统主容器的抗震性能研究尚未考虑容器内部流体与结构耦合效应的影响[6-8]。2009年意大利学者Frano等对于欧洲XADS项目容器罐体进行了流固耦合作用下的晃动分析和罐体屈曲分析[9]。上述研究表明:我们对ADS嬗变系统的抗震性能的认知还远远不足,仍需要进一步深入研究。
本文以ADS嬗变系统的反应堆主容器为主要研究对象,基于ABAQUS大型商用有限元分析平台, 采用 CEL(Coupled Eulerian-Lagrangian)方法研究主容器在地震作用下的动力响应特点,为ADS系统地震安全进行评价。
1 有限元模型
由于反应堆主容器内部保存大量铅泌液体,液体被约束在罐体和内部管道中,按传统的流固耦合分析方法分析,需要对液体进行非常复杂的网格处理,而采用CEL方法可以有效的简化对液体网格的划分。具体建模如下图1所示。模型内外罐体以及其连接部分建模采用实体单元(C3D4),共183 744个单元,材料为特种钢,密度为8 030 kg/m3,弹性模量为2.11×1011N/m2,泊松比为0.3,该模型边界条件为罐体顶部完全锚固。铅泌液体建模采用欧拉单元(EC3D8R)描述,CEL方法结合了拉格朗日单元与欧拉单元的优势,利用拉格朗日单元描述固体网格,保证耦合边界的节点运动,而欧拉单元适用于描述流体的大变形运动。
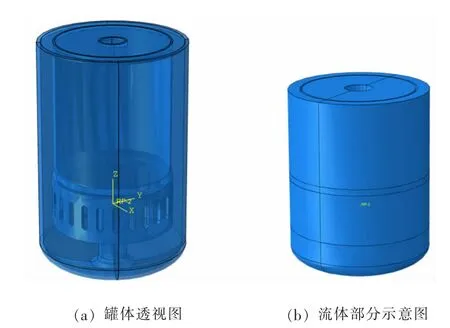
图1 罐体透视图及流体部分示意图Fig.1 Tank perspective and fluid section schematic
2 基于Mie-Gruneisen的us-up线性冲击模式[10]
对于模型中铅泌液体密度大、黏度高的特点,假定其液体流动为势流,因而可利用基于能量的状态方程(Mie-Gruneisen)求解其运动状态方程。如式(1):

式(1)中PH为冲击压力,EH为单位质量的冲击能量。由于本文中涉及流体为液体,故对于该类不考虑压缩的流体情况下,Γρ即为流体的初始物质常数Γ0。根据相关理论,冲击压力与冲击能量的关系式如下:

式(2)中, η 是标称体积压缩应变,η=1-ρ0/ρ,然后对(1)式的状态方程进行化简可以得到压力的表达式:
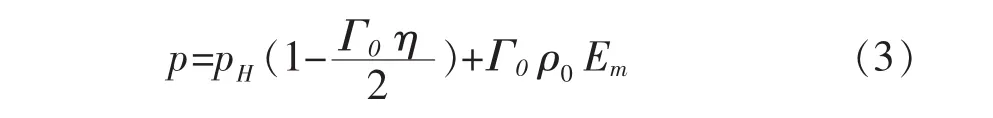

式(4)中c0与s为定义流体物质的剪切速度与粒子速度线性关系的两个常数,以上两个常数与流体材料有关,则对于线性冲击模式下的状态方程可化为如下表达式:
对于pH做出了一个拟合,表达式如式(4)所示:
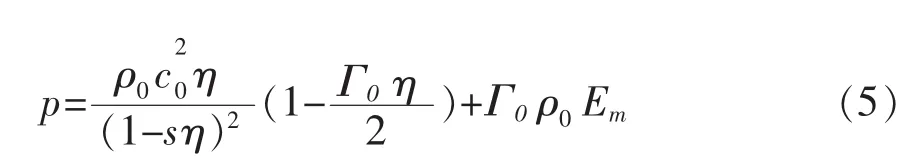
将状态方程转化成以上压力与能量的形式就可以在赋予初值的情况下在每个节点位置显式求解方程。
3 CEL方法
在传统的拉格朗日分析中,节点固定在材料内,单元随材料变形而变形。由于拉格朗日单元通常是单一材料,所以材料边界与元素边界重合。相比之下,在欧拉分析中,节点固定在空间中,物质流过不变形的单元。因此,欧拉单元中物质边界必须在每个时间步长内计算,且通常不与欧拉单元的边界相对应。
通常对于欧拉单元的分析涉及到物质的剧烈变形,而传统的拉格朗日单元会因为网格的高度失真而导致计算失去准确性。CEL方法通过将欧拉物质通过欧拉-拉格朗日接触与拉格朗日单元进行相互作用。
在CEL方法中,每个时间增量被分为拉格朗日阶段与欧拉阶段。在时间增量的拉格朗日阶段,假定节点固定在材料内,单元随着材料变形。进入欧拉阶段后,变形暂停,内置算法对存在显著变形的欧拉物质进行重新划分,并计算相邻的欧拉单元的物质流动。欧拉单元内的流动是基于体积流体来实现的,通过计算每个单元内的欧拉体积分数来跟踪欧拉物质运动,在每个时间步长内根据单元的欧拉物质体积分数通过界面重构算法得到欧拉物质的边界。物质在欧拉网格中流动时,状态变量通过势流在单元间传递,结合上一节中所提及的状态方程可求解相关参数。
CEL方法虽然可以对于液体网格划分做出有效的简化,但是该方法也存在相关的限制,例如拉格朗日单元与欧拉单元网格的匹配问题,当二者网格匹配性较差时,流体物质的边界重构算法会产生流体物质穿透拉格朗日单元的情况,因此CEL方法需要对拉格朗日单元与欧拉单元的网格匹配性上进行大量尝试,并根据相应结果总结其网格匹配性的规律,直至两种网格之间不再发生物质穿透。CEL方法的建模分析流程图如下图2所示。
4 地震动输入
该模型与传统储液罐底部地震动输入不同,该罐的地震动由顶部锚固区输入。本模型输入地震动为场地人工波,输入峰值为0.3 g,峰值对应时刻为3.1 s,输入加速度的时程曲线如图3所示。由输入地震动的频谱特性可知该地震波的频率集中在2.5 Hz左右。
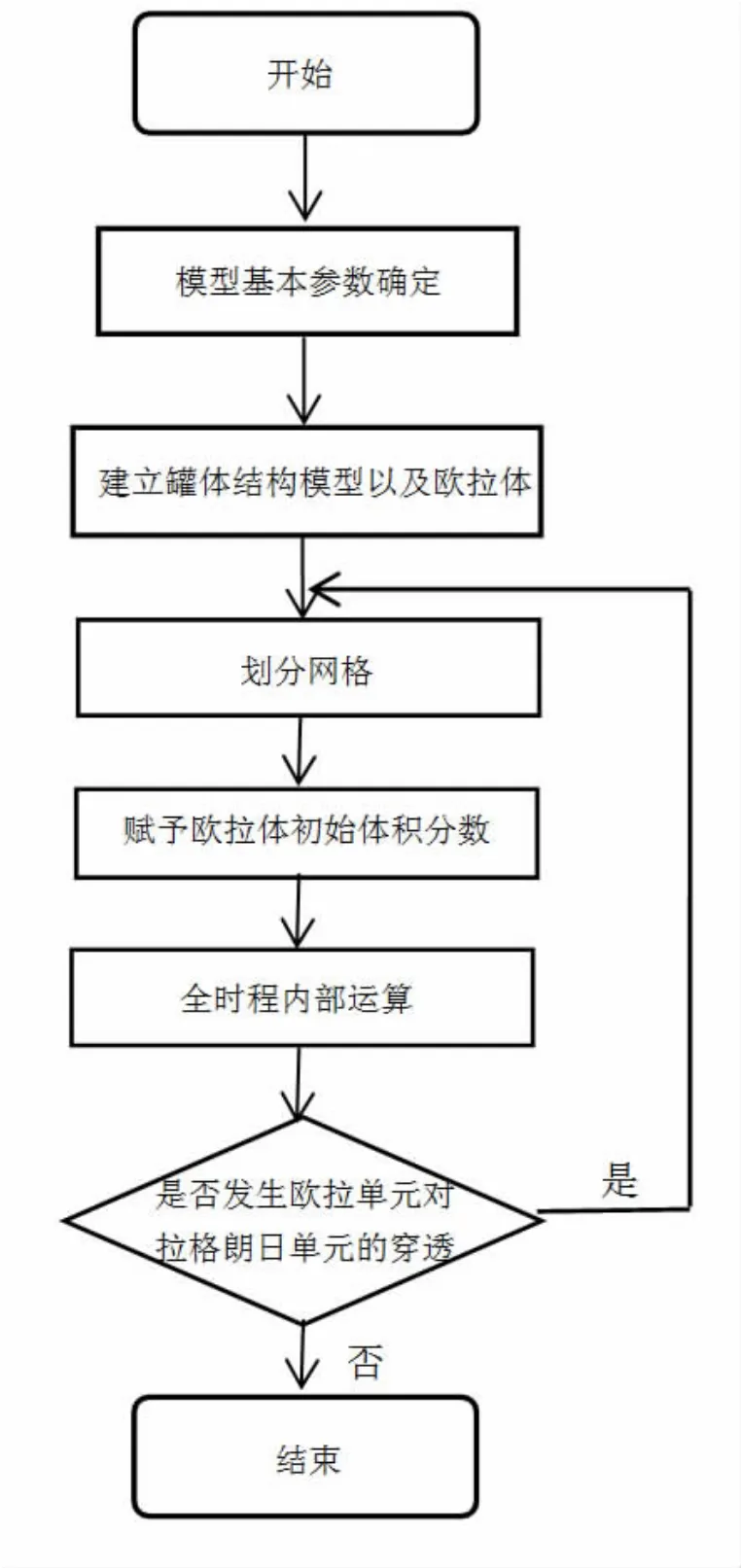
图2 CEL分析流程图Fig.2 CEL analysis flow chart
5 数值分析结果
由于地震动主要发生在前10 s,因此在本模型中对于结构主要进行前10 s的地震模拟,给出模拟中位移明显的时刻,得到模型中t=5 s时刻与t=8 s流体位移响应云图如图4所示,虽然强烈的流体位移响应没有对容器顶部造成较大冲击,但是剧烈的液体晃动对于罐壁将产生较高的动液压力。
强烈的地震动输入使结构的罐体产生了比较高的应力水平,根据模型得到结果选取了平均应力水平较高的一个时刻t=9 s应力云图如下图5,如图所示罐体四周的应力较为平均,但罐的连接处应力远大于罐体其他部分,内外罐的连接位置被破坏的可能性将远高于罐体侧壁破坏。在实际应用时,需要对于连接处位置考虑合理的柔性连接以防止可能发生的破坏。
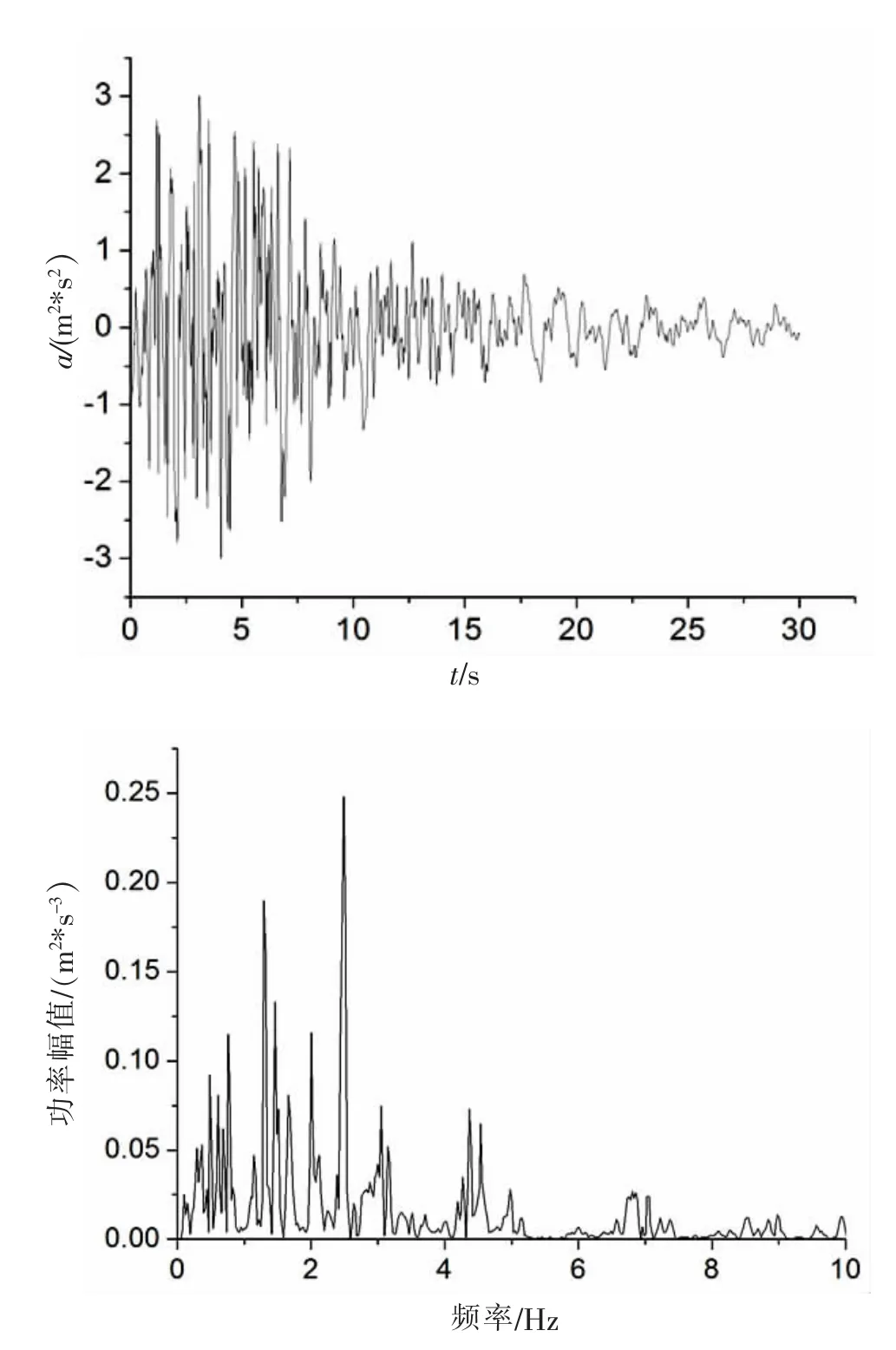
图3 加速度时程曲线及频谱Fig.3 Acceleration time history curve and spectrum

图4 流体位移响应Fig.4 Fluid displacement response
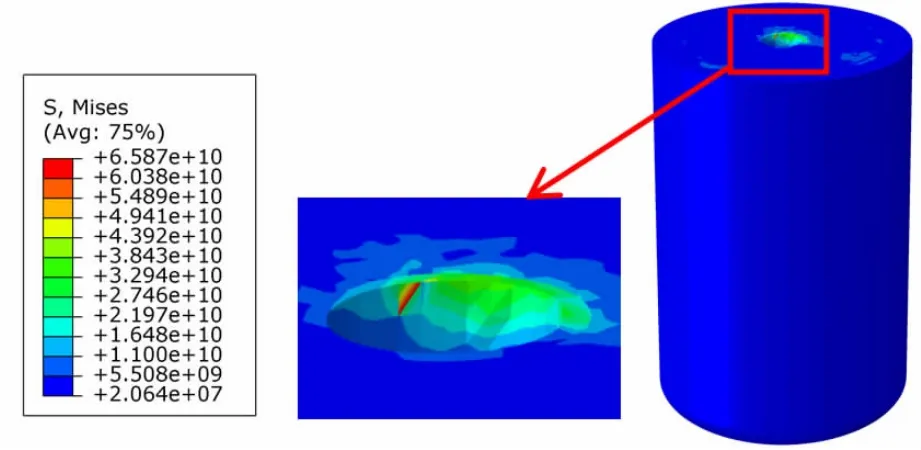
图5 t=9 s时刻应力云图Fig.5 Stress cloud map at t=9 s
本模型在输入地震动情况下产生了很大的动液压力,这个作用力将对于结构产生较大影响,甚至使结构发生一定程度的局部破坏。通过对于模型结构的反力进行输出,得到主容器对结构三个方向上的最大反力分别为:X向34.8×103KN,Y向18.1×103KN,Z向6.58×103KN。对结构各方向上的反力时程进行处理,可得到ADS系统主容器罐体在三个方向上的动力放大系数时程如下图6。
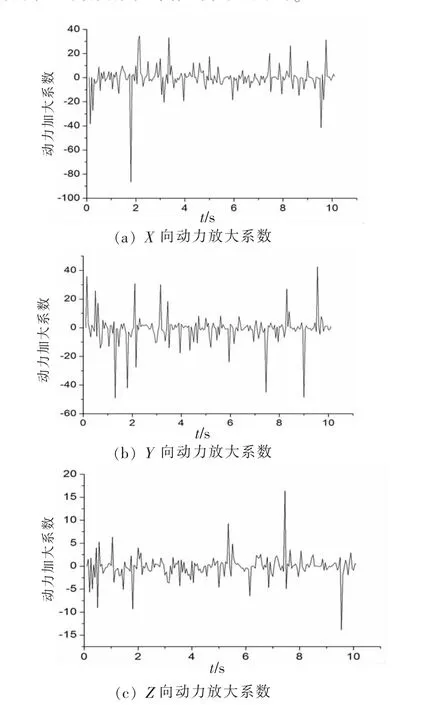
图6 主容器动力放大系数时程曲线Fig.6 Main container power amplification coeffcient time history curve
如图6所示主容器罐体在三个方向上均有显著的动力放大效应,如此剧烈的动力放大效应必定会破坏罐体与结构的连接,因此在实际应用中,应当做出适当的隔减震措施以控制主容器罐的动力放大效应。
6 结语
本文采用CEL方法对ADS系统主容器进行了地震作用下流固耦合分析,通过分析可以得到以下结论:
(1)采用CEL方法能较好地模拟地震动作用下反应堆主容器的流固耦合效应。
(2)罐体的平均应力水平较高,尤其在罐体的顶部连接处应力可能发生应力集中现象,可能会造成罐体局部破坏或者屈曲。
(3)容器内部流体晃动产生了显著的动力放大效应,增大了主容器对结构的地震作用力。
本文分析了ADS系统主容器罐在地震作用下的流固耦合反应,对于原型罐还存在着较多值得研究的问题,如主副罐耦合振动、罐结构合理连接形式等,都是值得未来继续研究的方向。
参考文献:
[1]温德超,郑兆昌,孙焕纯.储液罐抗震研究的发展[J].力学进展, 1995, 25 (1): 60-76.
[2]戴鸿哲,王伟,穆海燕,等.大型外浮顶立式储液罐被动控制方法[J].哈尔滨工程大学学报,2008,40(10):1 537-1 541.
[3]韩芳,龚相超,陈桂娟.基于流固耦合理论的立式储液罐抗震数值分析[J].武汉科技大学学报,2011,34(5): 359-363.
[4]林均岐,李山有,李宜瑞,等.立式储液罐地震反应数值分析[J].地震工程与工程振动,2006,26(4):152-155.
[5]刘春明.立式储液罐地震响应数值分析及基础隔震研究[D].武汉:华中科技大学,2013
[6]张洋.铅铋合金冷却反应堆主容器抗震性能分析[D].合肥:中国科学技术大学,2014.
[7]汤建楠.铅铋快堆双层容器抗震分析[D].北京:华北电力大学,2015.
[8] 刘璐.ADS零功率装置抗震力学分析[D].北京:中国科学院大学,2016.
[9]R.Lo Frano,G.Forasassi.Conceptual evaluation of fluidstructure interaction effects coupled to a seismic event in an innovative liquid metal nuclear reactor[J].Nuclear Engineering and Design, 2009 (239): 2 333-2 342.

