隔震剪力墙结构的有害层间位移角研究

滕晓飞，谭 平，周林丽，金建敏，李艳敏

（广州大学教育部工程抗震减震与结构安全重点实验室，广州 510405）

0 引言

我国的结构设计规范对建筑的稳定性和使用要求是通过对楼层名义层间位移角限值而进行控制的。楼层的名义层间位移角主要由构件侧向受力引起的有害层间位移角和因下部楼层转动引起上部楼层的无害层间位移角组成[1]。相关文献[2-4]指出国外高层建筑层间位移限值比国内要宽松，大量学者[5-9]通过对高层结构、超高层结构的仿真分析及工程实例进行研究并指出，无害层间位移角不能反应构件的实际受力状态也不会引起上部楼层的内力和变形，所以应对高层建筑的设计位移角进行放宽。但以上研究仅仅针对抗震结构而进行的。随着隔震技术的成熟和推广，其适用范围也由最初的多层建筑向越来越高的高层建筑发展。对于低矮的隔震结构，其上部结构往往类似刚体的平动；但随着上部结构高度和地震作用的增加，其弯曲变形或弯剪变形的特性越来越显著，隔震结构中有害层间位移角所占比重如何？是否可以像传统抗震结构一样进行放松？以有害层间位移角作为目标函数进行优化设计会对隔震结构整体性能产生何种影响？这些都是值得研究的问题。

本文基于矩形分布水平荷载模式的悬臂铁木辛柯梁模型推导了隔震结构的有害层间位移角和名义层间位移角的计算公式。对某高层隔震剪力墙算例的有害层间位移角和名义层间位移角的分布规律进行研究，分别以结构有害层间位移角和名义层间位移角为目标函数对上部结构进行优化设计，并对优化前后的设计方案进行用钢量和罕遇地震作用下的动力非线性时程分析，对两种优化方案的隔震层响应及塑性损伤演化规律进行评估并得出有益结论。

1 隔震结构的有害层间位移角公式

隔震结构在水平地震作用下往往会产生类似刚体的平动，其上部结构所受到的地震作用也往往沿高度形成类似矩形分布，但随着高度的增加其侧向变形也通常会包含越来越多的弯曲变形和剪切变形成分。结合剪切型和弯曲型模型的特点，可将高层基础隔震结构等效为悬臂Timoshenko梁模型[10]对其总的名义层间位移和有害层间位移进行计算，结构的等效计算模型如图1所示：

隔震结构遭受到水平地震作用q（x）时，任意高度x截面上的弯矩Mq（x）可表示为：

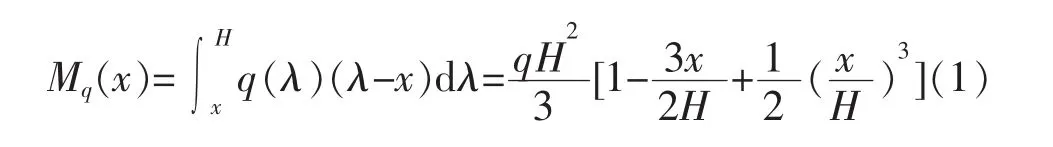
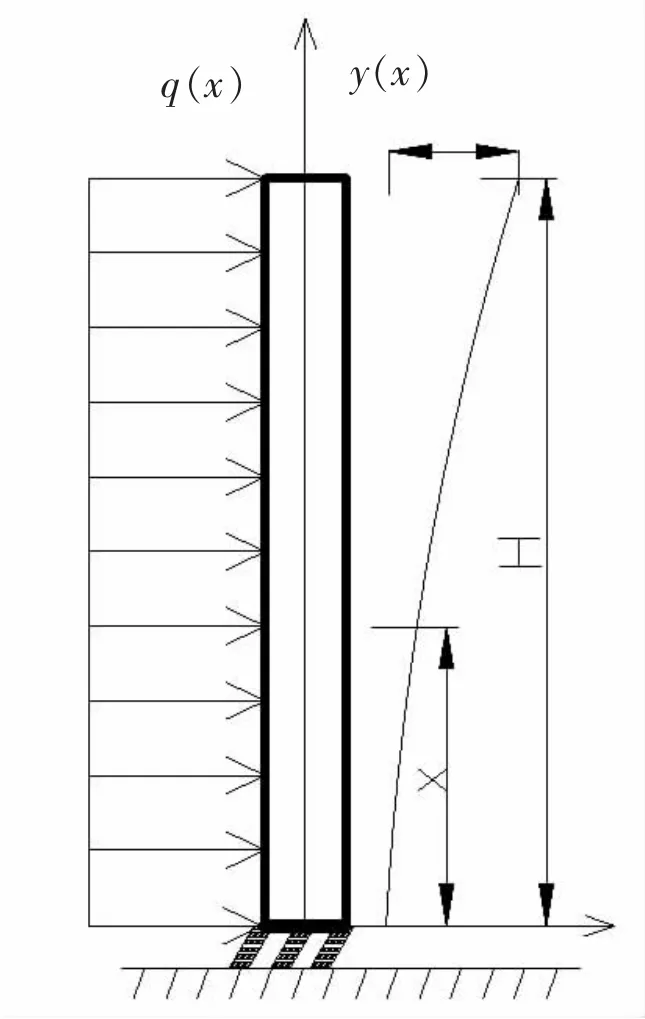
图1 隔震结构悬臂铁木辛柯梁模型Fig.1 Calculation model of isolation structure

假设悬臂铁木辛柯梁截面的抗弯刚度为EI，则任一高度x处的由侧向弯曲引起的变形yM（x）为：

任意高度x截面上的水平剪力Vq（x）通常可表示为：

通常混凝土矩形截面梁可取μ=1.2，G=0.4 E，则yV（x）可简化为：

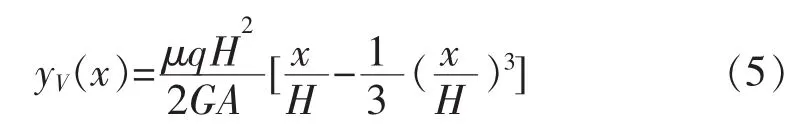
由于高层剪力墙结构中弯曲刚度和剪切刚度并非无穷大，因此在遭受水平地震作用时必然同时产生弯曲变形和剪切变形。因受力而引起的剪切变形和弯曲变形之和，即为水平荷载作用下高层结构的总体名义侧移位移，可表示为：

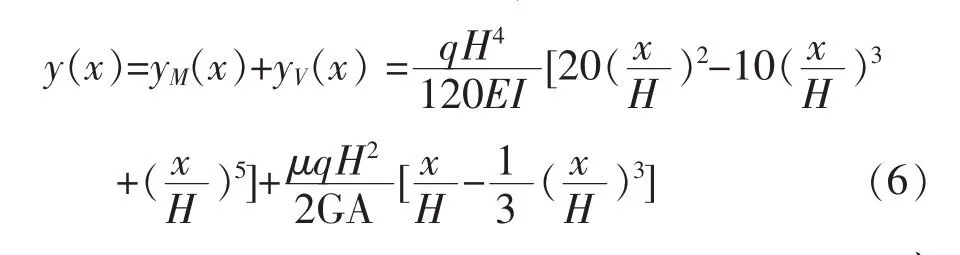
对整个高层结构来说，下部楼层往往会因弯曲转动而引起上部楼层的刚体转动。这种因刚体转动而产生的侧向位移包含在结构总体的侧向位移里，并从结构底层向上逐渐累积，但不会对构件的实际受力状态产生任何直接影响，故可把因下部第i-1层竖向构件弯曲转动而引起第i层的层间位移定义为无害层间位移，可由第i-1层竖向构件弯曲变形产生的无害转角θi-1求得[11]。结构楼层因受力而产生的有害层间位移可通过楼层总的名义层间位移和无害层间位移之差来求得。从这个角度出发可将高层结构的层间位移角分为：无害层间位移角、有害层间位移角和总体名义层间位移角。

在忽略结构扭转的影响下，结构的无害弯曲转角θi-1可根据结构轴向剪力墙平面内节点的垂直绝对位移之差和结构尺寸的比值进行确定：

结构的无害层间位移可表示为：

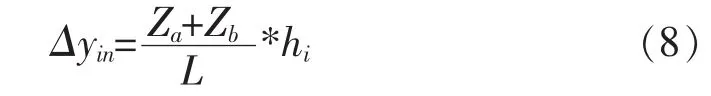
则结构的有害层间位移可表示为：

结构的有害层间位移角可表示为：

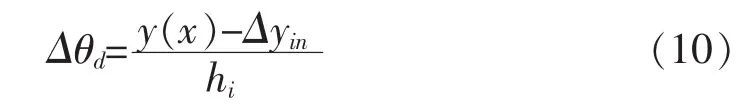
图2 有害层间位移角计算简图Fig.2 Calculation model of harmful interlayer displacement

2 算例概况

该算例为剪力墙结构，地上共18层（含隔震层），结构总高52.6 m，隔震层层高1.6 m，标准层层高3 m，结构平面尺寸为14.6 m×20.0 m，最大高宽比3.6，1-3层剪力墙墙厚300 mm，4层以上剪力墙墙厚200 mm，混凝土强度等级均为C35。抗震设防烈度8度（0.2g），II类场地，设计地震分组为第二组，场地特征周期为0.40 s。设计时考虑隔震结构的经济性最优目标，对上部结构的构件截面尺寸进行了优化，使得楼层最大弹性层间位移角接近抗震规范的限值（1/1 000）。结构的有限元模型如图3所示，隔震层布置图如图4所示。

图3 剪力墙隔震结构有限元模型Fig.3 Finite element model of shear wall isolation structure

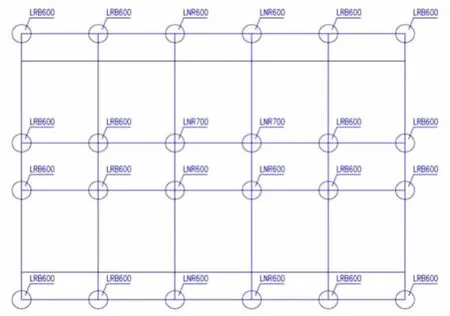
图4 隔震支座平面布置图Fig.4 Plane layout of isolation bearings

3 隔震结构有害层间位移分析

根据公式（8）和公式（9）分别计算隔震剪力墙结构的X向和Y向的有害层间位移和无害层间位移，从而得到不同楼层中有害层间位移所占的比例。具体计算过程如表1和表2所示，结构的有害层间位移和无害层间位移角如图5和图6所示。

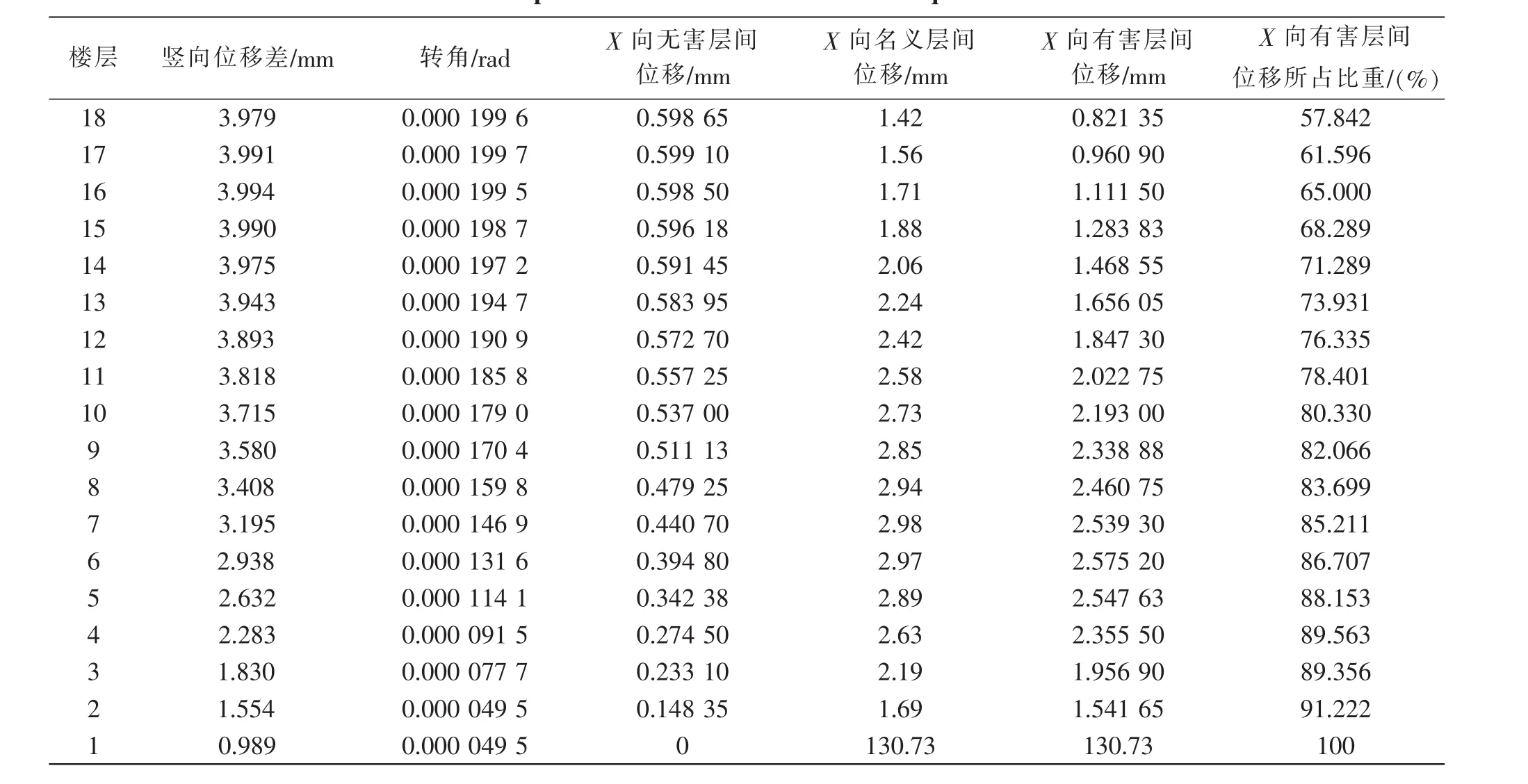
表1 X向地震作用下的有害层间位移和无害层间位移计算过程Table 1 The calculation process of harmful interlayer displacement and harmless interlayer displacement under X-direction earthquake

表2 Y向地震作用下的有害层间位移和无害层间位移计算过程Table 2 The calculation process of harmful interlayer displacement and harmless interlayer displacement under Y-direction earthquake

图5 隔震结构层间位移Fig.5 Story drift of isolated structure

对以上设计结果进行分析可知：剪力墙结构是由剪力墙和连梁共同组成的空间抗侧力结构体系，其中剪力墙的抗侧向刚度占主要部分，但隔震后上部结构所遭受的地震作用会相应减少，为考虑经济性最优目标而在墙体中开设了一定数量的洞口，使得隔震剪力墙结构中含有相当分量的框架剪切效应，因此整体结构呈现出弯剪型的变形特性。上部结构X向有害层间位移沿结构高度所占比例大于无害层间位移，Y向无害层间位移所占的比例在顶部1/6楼层以下的位置小于有害层间位移。

由表1和表2可知：上部结构最大名义层间位移和最大有害层间位移并不是出现在同一楼层的位置，但二者对应的数值相差不大，这是由于隔震剪力墙结构在遭受地震作用时，其所遭受的水平地震作用类似矩形分布，但在运动受力过程的同时也伴随着下部楼层弯曲变形的叠加，最终使得总体层间位移和实际受力产生的有害层间位移并不是发生在相同楼层的位置。通过对比最大有害层间位移及该楼层处的总体名义层间位移值可知：总体名义层间位移大于有害层间位移，采用总体名义层间位移角作为结构变形限值的控制指标的确可以保证上部结构的安全性，但具有一定的保守性。

4 不同层间位移角控制优化的用钢量分析

为了对比采用有害层间位移角控制与总体名义层间位移角控制方案对造价的影响，以最大有害层间位移角和最大名义层间位移角作为目标函数进行优化设计，在整体结构布局不变的情况下进行微调。优化之后两种隔震结构的上部计算配筋面积对比如图7所示。

图6 隔震结构层间位移角Fig.6 Story drift angle of isolated structure

通过对比二者的用钢量可知，优化后的结构总用钢量比原隔震结构有一定程度的减小，主要体现在抗侧力构件剪力墙的用钢量上。这是由于优化后的隔震结构以有害层间位移角控制为目标函数，减小了上部结构的抗侧力刚度所造成的。弹性设计控制位移放松了1.18倍，用钢量减小了13.4%，这对于降低工程造价是非常有益的。

5 有害层间位移角控制方案的损伤分析

结构在遭受强震作用后往往会进入损伤状态，进而会影响到结构的延性破坏模式和安全性。因此，罕遇地震下最关心的就是构件的损伤程度及其破坏次序。图8~图13列出了EL-Centrol波X向罕遇地震作用下有害层间位移角控制方案不同时刻的损伤演化云图。

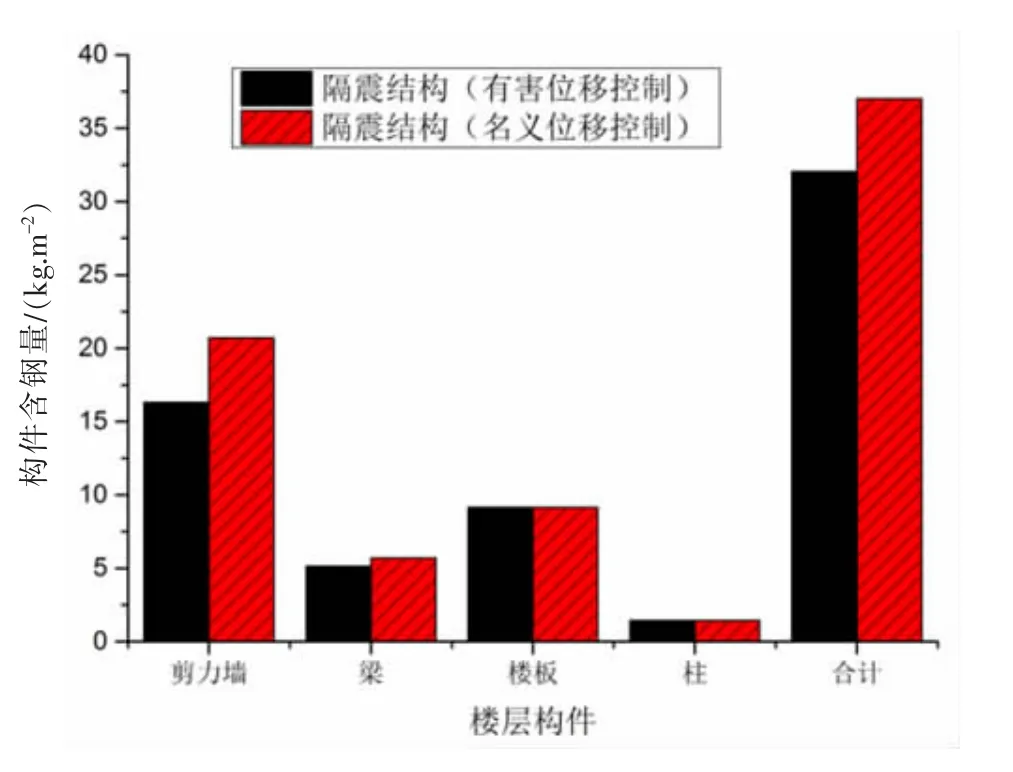
图7 不同方案的含钢量对比Fig7 Comparison of steel content of different schemes

图8 X向受压损伤云图（5 s）Fig.8 Damage nephogram of X（5 s）

图9 X向受压损伤云图（15 s）Fig.9 Damage nephogram of X（15 s）

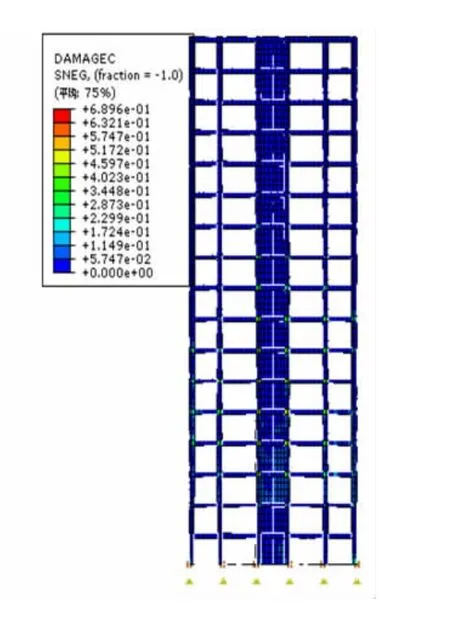
图10 X向受压损伤云图（30 s）Fig.10 Damage nephogram of X（30 s）

图11 X向受拉损伤云图（5 s）Fig.11 Tensile damage nephogram of X（5s）

图12 X向受拉损伤云图（15 s）Fig.12 Tensile damage nephogram of X（15s）

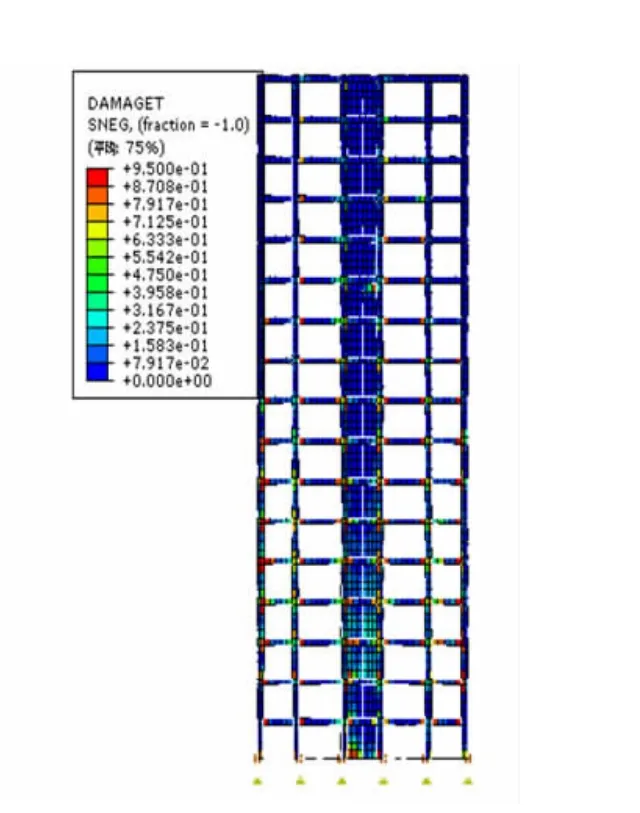
图13 X向受拉损伤云图（30 s）Fig.13 Tensile damage nephogram of X（30s）

通过对结构不同时刻的损伤演化云图的分析发现：有害层间位移角控制方案的隔震结构在X向罕遇地震作用下，首先在中部楼层的位置出现受拉/压损伤，主要体现在连梁端部构件上。随着上部结构的平移运动，损伤的位置进而向上下相邻的楼层发展，最严重的部位主要集中在连梁端部，这是由于连梁相对于剪力墙墙肢的刚度较小，在罕遇地震激励下产生了相当程度的有害层间变形，使其首先产生了转角并发挥耗能作用。同时连梁端部的弯矩和剪力也在一定程度上对墙肢的变形起到了约束作用，改善了整体墙肢的受力状态。在墙肢和连梁协同工作下，整个上部结构的损伤分布较为均匀，这对于隔震剪力墙结构在罕遇地震作用下的安全性是非常有利的。

6 结语

本文采用矩形分布水平荷载模式的悬臂铁木辛柯梁模型推导了隔震结构的名义层间位移角和有害层间位移角的计算公式。对某高层隔震剪力墙算例有害层间和名义层间侧移的分布规律进行研究，分别以结构有害层间位移角和名义层间位移角为目标函数对上部结构进行优化设计，并对优化前后的结构进行设计经济性和罕遇地震作用下的动力非线性时程分析，对两种优化方案的塑性损伤演化规律进行评估并得出以下结论：

（1）隔震剪力墙结构因墙体开设一定数量的洞口，会造成上部结构存在相应的弯剪变形特性，使得有害层间位移在总体层间位移中占据的比重大于无害层间位移，这种趋势自下而上逐渐减小。

（2）隔震剪力墙结构的最大名义层间位移和最大有害层间位移并不是出现在同一个楼层，但基本发生在相近楼层。最大有害层间位移所在楼层处的名义层间位移大于有害层间位移，采用最大名义层间位移角作为控制指标完全可以保证上部结构的安全性，但具有一定的保守性。

（3）以有害层间位移角为目标函数的优化设计方案可通过对构件截面的优化设计达到一定的经济性目标。其上部设计层间位移角放松1.18倍，整体结构的总用钢量比原来方案减小了13.4%，这对于降低工程造价是非常有益的。

（4）以有害层间位移角为目标函数的优化设计方案在罕遇地震作用下首先在中部楼层出现受拉/压损伤，进而向上下相邻的楼层发展，较严重的部位主要集中在连梁端部位置，整个上部结构的损伤分布较为均匀，这对于上部结构的安全性是非常有利的。

参考文献：

[1]傅学怡．高层建筑抗震设计(第二版)[M]．北京：中国建筑工业出版社，2010.

[2]郑建东，谢 春．某大高宽比高层剪力墙结构有害位移角计算及探讨[J]．建筑结构，2010，40(12)：83-86.

[3]蔡建，翁泽松．高层建筑结构层间位移角限值控制探讨[D].广州：华南理工大学，2014.

[4] D Weng，Y Jiang ， LU Xilin．Allocation of Viscous Dampers Based on the Harmful Inter-story Drift[J]．Structural Engineers，2014，30（01）：113-121.

[5]SW Shin，CK Jung，KS Lee．Control of Lateral Displacement for Super Tall Building by Floor&Partial 3D Br-ace[J]．Applied Mechanics&Materials，2013，284-287.

[6]XL Han，HX He，XX Tian．Control of Lateral Stiffness with Harmful Drift Angle for Structure with Transfer Storey[J]．Journal of South China University of Technology，2008，36(10)：6-11.

[7]郭子雄，林伟松.水平荷载作用下高层剪力墙结构无害层间位移分析[D]．泉州：华侨大学，2013.

[8]薛彦涛，章万胜，金林飞．结构受力层间位移(有害位移)计算方法研究[J]．建筑科学，2014，30（3）：1-7.

[9]邓明科，梁兴文，辛力．剪力墙结构基于性能抗震设计的目标层间位移确定方法[J].建筑结构学报，2008，25(11)：141-148

[10]宋晓，谭平，滕晓飞.基础隔震结构连续化模型研究[J]，河南大学学报（自然科学版），2017，47（02）：222-229.

[11]广东省建设厅.广东省实施高层建筑混凝土结构技术规程补充规定：DBJ/T 15-46-2005[S]．北京：中国建筑工业出版社，2005.

[12]中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010-2010[S].北京：中国建筑工业出版，2011.