物理教学两种思维的训练
张淑银
一、演绎思维的训练
演绎法是一种按照一定的逻辑规则从若干命题(前提)直接引出一个命题(结论)的推理方法,物理教学中针对高中生在演绎推理中直言推理成熟最早,假言、选言和复合推理发展同步,但成熟较晚,连锁推理发展最差这一特点,改革课堂教学模式,加强演绎训练,形成开放性教学模式。即教师设计出一种最优的教学程序:提出课题——分析猜想——实验、观察(创设一定的情境,形成一个体验、内化的习得过程)——建立概念——灵活运用。其相应的教学流程分六步进行(以高中《物理》《电磁感应》第一单元为例》
1.教师引出课题,学生自学本单元内容,独立思考设疑(20分钟,提出课题)。
2.学生间相互讨论、争论、答疑、教师随时和学生交流,共同商讨解决问题(20分钟,分析猜想)。
3.学生分两个一组在实验室做高中《物理》第四章《电磁感应》中部分图示实验。研究、探讨、再现规律和定律。教师巡回指导、解答学生问题(40分钟,实验、观察)。
4.学生以抢答和答辩形式回答教师提出的系列问题,一个问题可由多位学生不断补充回答,也允许学生辩论,直到学生认为满意为止(40分钟,建立概念)。
(1)怎样才能产生电流?你会采用哪些方法利用磁场来产生电流?说明实验所需要的仪器及实验步骤。
(2)产生感应电流的条件是什么?导体和磁场间有相对运动时,导体中是否一定会产生感应电流?为什么?
(3)法拉第关于电磁感应现象阐述了什么物理原理?
(4)电磁感应现象实验中的闭合回路有无电源?有的话是哪部分?
(5)产生感应电动势的条件是什么?感应电动势的大小与哪些因素有关?
(6)磁通量的变化量和磁通量的变化率有何区别和联系?
(7)法拉第电磁感应定律和导体做切割磁力线运动时感应电动势的表达式有无矛盾?为什么?
(8)应用法拉第电磁感应定律E=Blvsin0和E=n△φ/△t n解决有关问题时,什么情况下适合应用公式E=Blvsin0?什么情况下适合应用公式E=n△φ/△t n,什么情况下两式通用?
(9)如何计算感应电流的大小?
(10)如何判断感应电流的方向?
(11)楞次定律中“阻碍”的因果关系是什么?“阻碍”能否理解成“阻止”?如果引起感应电流的磁通量的变化被阻止了,感应电流还会继续产生吗?为什么?
(12)(教师在平台实物展示仪上分别做磁铁靠近轻质闭合铝环A和不闭合B环的演示实验后,提问学生)。磁铁靠近B环时,B环为何不动?
(13)应用楞次定律确定感应电流的方向有哪几个步骤?
(14)应用右手定则确定感应电流的方向有哪几个步骤?
(15)在电磁感应现象中能量是怎样转化的?能量是否守恒?举例说明。
5.老师小结。围绕本单元的重点、难点,结合学生回答的不足之处进行系统性的小结(建立概念)。
6.学生课堂检测。共做四道选择题、四道选择题、两道计算题(25分钟)。作业布置:练习一、练习二、练习三中的选择、判断题在课堂自学时完成,计算题为书面作业。
该教学设计的特点为:不是把教学建立在学生已有的发展水平上,而是把教学建立在学生尚未完全成熟的心理机能的基础上,让学生有目的地进行观察、抽象思维和随意注意等,使教学跑在发展的前面。
——教师在教学“舞台”上最大限度地“导演”,训练他们的演绎能力。首先,系列问题设置符合有台阶、循序渐进的原则。其次,各推理能力符合反复循环训练、此起彼伏、最后掀起高潮的原则,从而强化学生的演绎训练,促进归纳和演绎能力的均衡发展。
学生的习得活动符合内化→外化→内化的原则。即:让学生不通过活动接受外界影响,同时也通过活动反作用与外界。从而发展学生的高级心里机能。
二、创造思维的训练
创造性思维是应用独特的、新颖的方式解决问题的思维活动。它包括发散思维和集中思维。发散思维是通过对若干概念的重新组合,散发出两个或多个可能的答案或设想,具有流畅性、变通性和独特性的特点。在物理教学中应诱导学生进行创造性想象,开发学生创造思维。
1.提供原型,培养发散性思维的流畅性。让学生在短时间内表达较多的观念、思考的途径、或解决问题的多种方法。
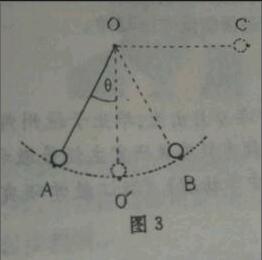
例:长为L不可伸长的轻绳,一端固定咋O点,另一端系一个质量为m的小球,最初小球位于A点,细绳伸直且与竖直面成θ角度。将小球由静止释放,小球将在竖直平面内的A、B两点间摆动,A、B两点于同一水平面。为了使小球由A点静止释放后能达到水平位置的C点,则在O处至少需给小球多大的水平冲量?
解:分析该题的关键是要理解“至少”的物理含义。即,小球在A点处静止释放后能到达水平位置C点,在O所给的冲量必须符合以下条件:①冲量的方向水平向右;②小球到达C点时的速度恰好为零。
根据系统机械能守恒可知:
A→O mgL(1-cosθ)=1/2mvO2
O→C 1/2mvO2 =mgL
由此两式解得:
冲量1≧m√2gl(1-√1-cosθ)
2.进行诱发思维,培养发散思维的变通性。让学生思路发生变换和变通,使学生解决问题不受思维定势的影响。针对上题而言教师通过变换物理情境进行诱发:、
(1)若在O处给小球的水平向右的冲量大于m√2gl(1-√1-cosθ)时,小球可能作何种运动?按绳断和绳不断两种情况讨论。
(2)若在O处给小球以水平向左的冲量时,则至少需给小球以多大的冲量,才能使小球经过C点(假设绳不断)?小球经过C点后将作什么运动?
(3)若将该系统放入场强方向竖直向下的匀强电场中,且讓小球带上正电荷,水平方向施加的冲量会发生什么变化?
(4)请同学们根据所学的知识和规律思考一下,还要以通过变换那些物理情境来进一步研究小球的运动情况?
3.开展创造思维、培养发散思维的独特性。让学生自己提出奇特的、新颖的思路,对问题提出独创见解。在教师的诱导下,学生思考变换物理情境后提出下列设为并进行研究:
(1)让小球带负电荷后仍在原电场中运动,然后分qE>mg;qE (2)让带电小球在磁场中运动,然后分qvB>mg;qvB (3)还可让带电小球放入电磁场和重力场的混合场中来进行研究。 4.引导集中思维,使之指向正确的答案。通过求解、诱思、创思,让学生分析小球在各场中的运动特点,归纳出该系列题的答案——物体运动的形式是多种多样的,物质及其运动形式的发展,由量变到质变,但无论怎么变,问题万变不离其宗,即遵循一定物理规律,这些规律时可知的,以上所举例题遵循能量守恒定律。

