考虑循环温度影响下注水泥流变性能计算方法
徐璧华, 冯青豪, 谢应权, 杨玉豪
水泥浆的流变性能在固井过程中有着很大的影响[1-2],然而随着井深的不断增加,水泥浆承受的温度和压力越来越高,水泥浆高温、高压流变性受到的重视也越来越大[3-7]。在以往的研究和现场施工设计中,使用的水泥浆流变性计算方法[8-10]大多都没有考虑温度和压力对水泥浆流变性的影响,而流变参数是注水泥计算的重要参数,如不考虑温度和压力对流变性的影响,流动计算将会产生较大误差,因此对于高温、高压下影响水泥浆流变参数的计算,以及流动计算方法的研究具有重要的意义。
1 实验方案
实验主要仪器:水泥浆高温高压流变性的测试采用美国Chandler公司生产的7400型高温高压流变仪。
实验水泥浆:选取了一种常用的水泥浆,其配方为G级水泥+1%分散剂+5%微硅+2%降失水剂+0.1%消泡剂+水,水灰比为0.44。
实验条件:实验选取的温度为:27℃、 50℃、75℃、 90℃、 120℃、 150℃、 175℃ ;压力为常压、20、 40、 60、 80、 100 MPa。
2 温度、压力对水泥浆流变性的影响
温度和压力对水泥浆流变性能的影响见表1和表2。温度对水泥浆流变曲线的影响见图1。

表1 温度对水泥浆流变性能的影响

表2 压力对水泥浆流变性能的影响

图1 水泥浆的流变曲线(压力60 MPa)
由表1可以看出,温度对水泥浆流变性能的影响比压力大得多,随着温度的增加,塑性黏度和静切力明显下降。由表2可以看出,压力增加,塑性黏度及静切力虽有增加,但不明显。因此,考虑温度对流体流变参数的影响,是准确设计高温高压深井流体流变性的重要影响因素。如应用常温测量的流变参数,进行高温高压深井流变设计,将会带来比较大的误差。由图1可以看出,温度曲线变化十分明显,温度升高,曲线的斜率降低,使黏度减小。
3 考虑温度影响后流体流变性的计算
3.1 考虑温度后流体剪切应力计算
通过温度、压力流变实验可看出,钻井液、水泥浆的流变性要随温度发生变化,因此计算各流变模型的流变参数也必须要考虑到温度的影响。但实际作业时不可能通过实验方法确定每一温度压力下的实际流变曲线,并计算出流变参数。为此,通过大量的实验数据分析与研究,发现高温下流体流变性能的变化主要体现为流体剪切应力的变化,从图1可以看出,剪切应力是以指数形式变化,为此建立了不同温度影响下的流体剪切应力变化模型,可用下式表示:

式中,τ为任意温度下的剪切应力;τ0为常温(或某已知温度)测定的剪切应力;b为温度系数。
使用式(1),预测高温下液体的剪切应力的具体步骤如下:①选取2组温度,如常温27 ℃和75 ℃,在不同剪切速率下,测出对应的剪切应力,见表3。②计算温度系数b。③将b值代入式(1),可以计算出相应剪切速率下,其他温度的剪切应力值。


表3 旋转黏度计剪切应力读值
不同剪切速率下的b值是不一样的,如预测其他剪切速率情况下,某温度的剪切应力值,则应按上述方法,先计算温度系数b值,再计算此温度的剪切应力数值。
表4是4种不同密度水泥浆不同温度下,剪切速率为1 022~340.65 s-1测出的剪切应力和应用式(1)、(2)的温度预测方法,计算出相应的剪切应力的比较结果。
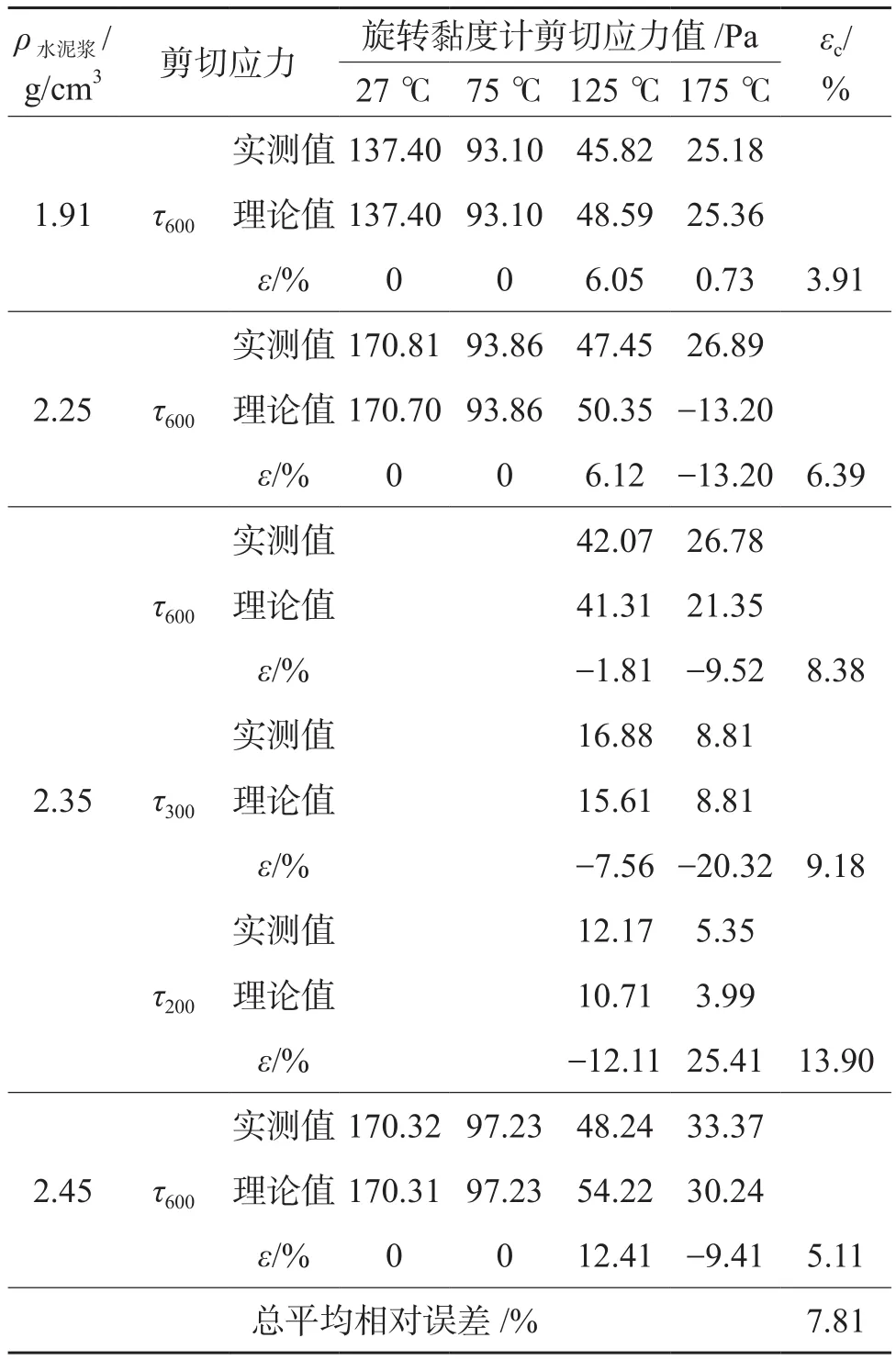
表4 不同温度下实测剪切应力与推导值的比较(14 MPa)
由表4可以看出,通过该方法计算的不同温度下, 某一剪切速率的剪切应力, 其总的相对误差为7.81%, 说明该计算方法可以用来考虑温度对剪切应力的影响。
3.2 不同温度下流体流变参数的计算
3.2.1 宾汉流体
用于钻井液流变参数计算:

用于水泥浆流变参数计算:


3.2.2 幂律流体
用于水泥浆流变参数计算:

用于钻井液流变参数计算:

式中,φ600、φ300、φ100为旋转黏度计在600、300和100 r/min测得的格数;ηst、ηst'为任意温度下的塑性黏度,Pa·s;τot、τot'为任意温度下的动切力,Pa;b为剪切速率为1 022 s-1的温度系数,1/℃;b'为剪切速率为511 s-1的温度系数,1/℃;b"为剪切速率为170.3 s-1的温度系数,1/℃。
3.3 考虑温度后注水泥流动计算方法
分析研究表明,水泥浆的流变性随温度压力变化十分明显,温度对流动计算结果的影响非常显著。水泥浆在不同的温度下,不仅其流变性能要发生变化,而且其他性能(如水泥浆稠化时间、失水量、自由水等)也要发生变化,有关文献研究表明,当水泥浆所受实际温度与进行实验时的温度相差5 ℃~10 ℃时,其水泥浆的性能将发生较大变化。
注水泥设计均只考虑井底循环温度和静止温度,这对于保证水泥浆性能,保证施工安全是必要的。对于流动计算,可采用上面介绍的上下水泥面平均温度来进行简化计算,但最合理的方法还是按温度变化分段计算,不过这种计算相当复杂,需使用计算机软件来实现其应用。
1)分段原则。保证温度变化在某一范围,称为温度变化限制范围。该值一般取5 ℃~10 ℃。
2)分段方法。设循环温度随井深的变化规律为:

它预测的准确性与地层、井眼、钻井液、水泥浆的热导率,施工过程循环排量等众多因素有关。
该方程建立其反函数式为:

这样,将循环温度从井底与水泥面深之间按要求温度范围分段后,即可求出相应井深的分段参数。

式中,BHCT为井底循环温度,℃;TTOC为水泥面深度循环温度,℃;△T为允许温度变化范围,℃;n为井段可分段数;Tm为第m井段底部的循环温度,℃;Hm:第m井底底部深度,m。如果循环温度变化函数中没有包括井斜的影响,则分段时应考虑井斜。
4 现场应用
表5是几口现场应用井的计算情况,从表中可以看出,考虑分段温度对流变性影响后其流动摩阻计算结果有所变化,更接近现场实际。
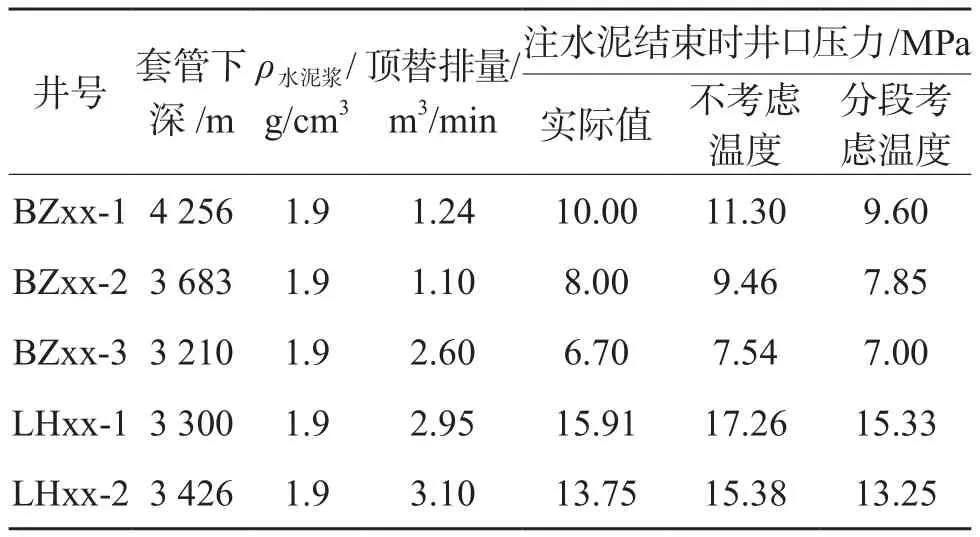
表5 现场注水泥流动摩阻计算
5 结论
LIU Xisheng. Drilling technology principle (Part Ⅱ)[M].Beijing : Petroleum industry press, 1988.
[2]刘崇建.国外油井注水泥技术[M].成都:四川科学技术出版社,1992:131-141.
LIU Chongjian.Foreign oil well cementing technology[M].Chengdu : Sichuan Science and Technology Press,1992:131-141.
[3]RAVI K M, SUTTON D L. The relationships of the rheological properties of cement slurries and temperatures[C]. SPE 20449.
[4]王伟,黄伯宗.高温高压下水泥浆的流变性及其模式[J].油田化学,1994,11(1):19-21.
WANG Wei, HUANG Bozong. The rheological properties and model of high temperature and high pressure water mud[J]. Oil Field Chemical, 1994, 11(1):19-21.
[5]何世明, 刘崇建,邓建民,等.温度压力对水泥浆流变性的影响规律研究[J].石油钻采工艺,1999(6):4-6.
HE Shiming, LIU Chongjian, DENG Jianmin, et al. The influence law reserarch of slurry rhelolgy of temperature and pressure[J]. Oil Drilling Process,1996(6):4-6.
[6]郭晓阳,刘崇建.非牛顿流体流变模式的研究[J].天然气工业,1997,17(4): 43-49.
GUO Xiaoyang, LIU Congjian. Non newtonian fluid rheological model research[J]. Natural Gas Industry,1997,17(4):43-49.
[7]中华人民共和国石油天然气行业标准,SY/T5480-92.注水泥流变性设计[S],第一版.北京:石油工业出版社,1993.
People's Republic of China Oil and Gas Industry Standards, SY/T5480—92. Cement rheological design[S], the first edition. Beijing : Petroleum industry press, 1993.
[8]陶谦,周仕明,张晋凯,等. 水泥浆流变性对水平井固井顶替界面的影响——基于天河一号大规模集群计算平台的数值模拟[J]. 石油钻采工艺,2017,39(2):185-191.
TAO Qian, ZHOU Shiming, ZHANG Jinkai, et al.Effect of rheological property of slurry on cementing displacement interface of horizontal well: the numerical simulation based on large-scale cluster computing platform Tianhe-1[J].Oil Drilling & Production Technology, 2017, 39(2): 185-191.
[9]American Petroleum Institute[S], API Specification 10,5th edition, Tex-as, U.S.A. 1990.
[10]ERIK B, NELSON. Well cementing[M]. Texas, USA :Dowell Sohlumberger Educatiaon Service, 1990.

