以图形分析法为基础的初中几何解题探究

卢胜容

【摘要】本文论述在引导学生解答初中数学几何题时，教师要对学生的解题过程进行指导，引导学生分析图形，开展变式训练，不断提高学生解决几何题型的能力。基本图形分析法重在探索解题思路的形成过程，帮助学生掌握几何原理，培养学生的思维能力，达到举一反三、轻负高效的良好效果。

【关键词】几何题型 图形分析法 分离图形 构造图形 添加辅助线

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2017）02A-0079-02

很多初中生认为几何难学，他们在解答几何题目时面对各种形状的图形、各式各样的符号和条件，经常会感到一头雾水，找不到解决问题的突破口，不但影响了考试成绩，还打击了学好数学的积极性和自信心。鉴于这种情况，教师要对学生解答几何题的过程进行指导，引导学生分析图形，展开变式训练，让学生轻松应对几何图形题目。下面结合具体例题来谈一谈以图形分析为基础的几何解题策略。

一、根据已知条件分离图形，结合图形性质解题

解答几何题目需要具备良好的逻辑推理能力，只有对题目中的已知条件和求证问题进行灵活恰当地转换，才能快速地解答。角平分线是初中几何中一个重要的知识点，很多几何题目都围绕着这个知识点进行设计，在中考试题中也不乏角平分线的影子。一些学生因为对角平线的性质等内容掌握不够扎实，导致在遇到这一类几何题目时无从下手。因此，教师要引导学生分析题目的来龙去脉，通过分离图形把题目转化为学生熟悉的基本图形，再结合图形的性质进行解答。

例如，教师出示了一道典型的角平线的题目：如图1所示，在四边形ABCD中，AD∥BC，BD平分∠ABC，求证：AD=AB.学生看到这个题目之后，有的学生发现求证的问题是AD、AB两边相等，而且两条边同属于三角形ABD中，因此可以把求证结论转化为求证∠ABD=∠ADB.通过这种求证命题的转化，使看似没有头绪的问题变得简单了。学生根据角平线的定义，推理得到∠ABD=∠DBC，同时根据AD与BC平行的条件，推理得到了∠ADB=∠DBC，由此得到了∠ABD=∠ADB.在三角形ABD中，∠ABD=∠ADB，所以这个三角形是等腰三角形，即AD=AB.在学生完成了解答之后，教师再让学生回顾解题过程，梳理解题思路：先看题目求证的问题是三角形ABD中的两条边相等，这时就可以把这个三角形分离出来了，通过逆向推理，只需要证明三角形的AD、AB两条边所对应的角相等，就可以根据等腰三角形的性质轻松解题。最后，教师引导学生总结：由这道题可以发现在解答一些含角平分线的题目时，可以根据已知条件把问题转化为，分离出一个图形，再利用这个图形的基本性质解答问题。

由上例分析可知，这种题目可根据已知和未知对问题进行转化，分离出简单的图形，使求证的问题一目了然。学生在找到解题突破口之后，就自然而然地顺利答题了。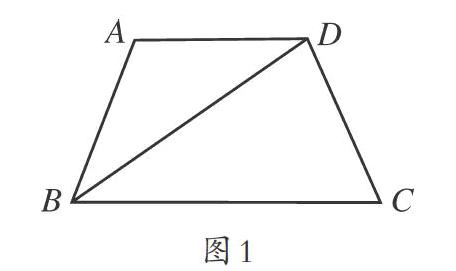

二、添加辅助线构造图形，利用几何知识解题

添加辅助线也是初中几何题解答中常用的方法，对很多学生来说，添加辅助线的题目都属于难度比较大的题目，因为他们并不清楚在哪里添加辅助线是最合适的。因此，教师在指导学生运用添加辅助线的方法解答几何题目时，不但要让学生明白辅助线添在哪儿，还要使学生透彻地理解为什么要添在那，让学生掌握添加辅助线的技巧。通常来说，很多复杂的几何题目在添加辅助线后，都会变得容易起来，因为通过添加辅助线构造了一个新的图形，使原来需要求解或证明的问题发生了转化，让学生找到了答题的方法。

例如，在学生学习了梯形的相关知识之后，教师出示了一道典型的中考题。如图2所示，梯形ABCD中，AD∥BC，一条腰AB长为2.5厘米，长底边BC长为4厘米，连结B、D两个顶点，作∠BAD的平分线与线段BD相交于点E，连结AE，如果AE∥CD，那么AD长多少？很多学生一看到这道题给出了这么多已知条件就不知所措了。此时，教师要引导学生再次读题，让学生发现已知梯形的一腰、一底的长度，求另一底的长度，但学生还是找不到从哪里下手解题。此时，教师引导学生在练习本上准确地把这个图画出来，学生画完图之后，教师又让学生把题目中的已知条件标示在图形中，让学生尝试看能不能把问题进行转移。在教师的点拨下，有些学生已经想到了通过延长∠BAD的平分线AE到BC边，与BC相交于F点，这时就可以把AD转化成FC了。此时马上有学生大胆推测：只要求出BF的长度，问题就迎刃而解了。可是，怎么求BF的长度呢？学生继续观察发现在三角形AFB中，∠BAF=∠FAD，∠FAD=∠AFB，所以，∠BAF=∠AFB。根据等腰三角形的性质，推导出AB=BF，则FC=BC-BF，即AD=BC-AB=4-2.5=1.5厘米。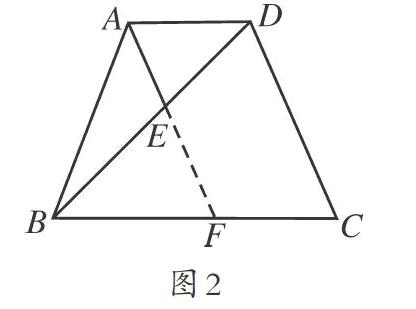

在教师的引导下，学生一边看图一边思考，通过合理地添加辅助線，找到了答题的关键点，然后把求解的问题进行转化。在这个过程中，添加辅助线是最关键的一步，借助辅助线构造了新图形，让原本需要求解的问题变得清晰明了。

三、借助旋转方法抽取图形，借助图形分析解题

旋转作为物体位置移动的一种常见方式，对发展学生的空间想象力具有重要的作用。在几何题中，有些已知条件比较繁杂，要求的问题看上去也与已知条件没有关系，这时学生往往都会感觉到束手无策。要解决这一类型的几何题目，需要学生的数学思维具有较强的灵活性，再根据题目的意思，借助自己的空间想象力，运用旋转的方法，从中抽取图形，并结合图形的性质把看似复杂的问题简单化，提高解题效率。

例如，在九年级总复习中有这样一道题：如图3所示，在正方形ABCD中，E点在正方形内部，分别把E点与A、B、C三个顶点相连，得到了△ABE，然后把这个三角形绕B点进行顺时针旋转90°，得到△CBE′。已知AE=1，BE=2，CE=3，求∠BE′C是多少度？学生根据题意先画出了草图，在画图的过程中，就有学生发现了△ABE旋转90°，其实就是AB边旋转到了BC的位置，BE旋转到了BE′的位置。因此很多学生就想到了把EE′两点连接起来，就得到了一个等腰三角形，再根据BE旋转90°得到了BE′，所以∠EBE′=90°。此时，很多学生会发现∠BE′E=45°，只要再求出∠EE′C的度数就可以了。根据勾股定理EE′2=BE2+BE′2=8，而在△EE′C中，EC=3，E′C=1，EE′2=8，根据勾股定理可知，△EE′C是直角三角形，则∠EE′C=90°，从而推算出∠BE′C=45°+90°=135°。

在解答这类题目时，学生的大脑很容易受到题目信息的干扰，思路不清晰，找不到解题的突破口。通过旋转图形，结合想象，就可以发现已知条件与求解问题之间的联系，从而通过层层推导，得到求解的答案。

总的来说，图形是几何学习和研究的核心内容，几何题的解答离不开图形性质的分析和各种定理的应用。教师在指导学生解答几何题目时，需要有意识地教会学生思考的方法，引导学生对已知条件进行分析，抓住要点，抽丝剥茧，把复杂的问题简单化，把未知的内容已知化，学会举一反三，做到触类旁通，不断训练学生的逻辑推理能力，提升学生的数学思维品质。