捷联惯导系统静基座的高精度初始对准方法
王雪瑞,周 岩
(河南工程学院 计算机学院,河南 郑州 451191)
捷联惯导系统静基座的高精度初始对准方法
王雪瑞,周 岩
(河南工程学院 计算机学院,河南 郑州 451191)
针对捷联惯导系统静基座初始对准存在精度低的问题,通过加速度计和陀螺仪获得重力矢量和地球角速度矢量,采用解析方法快速地估算出一个满足要求的初始姿态矩阵。借助卡尔曼滤波模型对系统的误差进行分析,并建立系统的状态方程和量测方程,将系统失准角从干扰误差中估算出来,为导航计算提供精确的初始条件。仿真实验结果表明,将卡尔曼滤波技术引入到捷联惯导系统静基座的高精度初始对准过程中,使对准精度和收敛速度均得到了显著改善。
捷联惯导系统;静基座;初始对准;卡尔曼滤波;精对准
捷联式惯性导航系统(SINS)是新型航位推算系统,具有自主性高和实时性强的优势[1],但也存在积分误差随时间逐渐积累的致命缺点。为了保障SINS的正常运行,需要在系统进入正常运行之前进行初始对准,如装定初始速度和位置、确定初始姿态角、惯性器件的漂移和标定等,为系统进入正常导航状态提供初始信息[2-3]。捷联惯导系统初始对准的精度直接影响着系统的导航精度,为了能够提高导航精度,只有尽可能的将失准角从干扰误差中估计出来,并进行补偿[4]。初始对准由粗对准和精对准组成[5]。粗对准通过加速度计和陀螺仪获得重力矢量和地球角速度矢量,再利用解析方法快速直接估算出一个满足要求的初始姿态矩阵,然后再将卡尔曼滤波引入到精对准的处理中,对系统误差进行分析,最终将系统失准角从干扰误差中估算出来,大大提高了对运载体的导航精度。
1 初始对准工作原理
对文中涉及到的4个坐标系进行定义:地理坐标系(简称g系)、载体坐标系(简称b系)、导航坐标系(简称n系)、导航计算坐标系(简称p系)[6-7]。
1.1 解析式粗对准



并记:

(1)


(2)


(3)

(4)
粗对准的目的是为了快速地获得初始姿态矩阵,但该姿态矩阵往往受到各种误差的影响,且误差较大,仍需对准。
1.2 精对准

图1 精对准原理框图

2 基于卡尔曼滤波的精对准方法

(5)

2.1 精对准状态方程的建立


(6)


(7)

姿态矩阵计算值:

(8)
其中:(φn×)为φn构成的反对称矩阵,又因为

(9)
将式(7)、式(8)代入式(9),并略去关于φn得:

(10)
又有:

(11)


(12)


(13)


(14)
考虑到关于陀螺仪测量和加速度计测量的误差假设,将陀螺漂移和加速度计的零偏都看作随机常数扩充到状态中,可得SINS静基座初始对准状态方程:

(15)



2.2 精对准量测方程的建立
若忽略所有的误差,那么测量当地加速度在导航坐标系下的理论值为:

(16)
但在计算过程,系统的姿态矩阵存在一定的计算误差和加速度计本身的测量误差,实际上加速度计的输出在导航计算坐标系下的投影为:
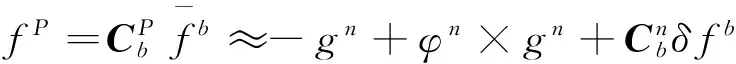
(17)
其中:δfb为加速度计在b系下的测量误差;b为加速度计在b系下的常值漂移误差;为加速度计在b系下的随机误差。加速度计的测量误差可表示为:δfb=,并记b和。
由于导航计算坐标系下的天向方向下的比力测量分量值和水平方向上的姿态角误差之间的耦合性非常弱,因此对天向方向上测得的加速度分量不予考虑,展开式(17)可得:

(18)

Z(t)=HX(t)+v(t)。
(19)

2.3 卡尔曼滤波方程的离散化
离散卡尔曼滤波基本方程如下所示:

图2 卡尔曼滤波计算流程图
其中:Kk为卡尔曼滤波器的增益矩阵;Pk为Xk的均方误差阵;Qk为系统过程噪声的协方差矩阵;Rk为系统量测噪声的协方差矩阵[13]。
卡尔曼滤波计算流程图如2所示。
3 仿真结果及分析
假定载体静止在经纬度为(40°,60°),3个初始姿态角分别为60°、80°、70°,加速度计零偏为x=y=100μg,陀螺仪漂移为εx=εy=εz=0.02°/h。初始水平和方位失准角分别为0.5°、0.5°、1°,卡尔曼滤波器中系统噪声方差阵为:Q=diag{(0.01°/h),(0.01°/h),(0.01°/h),0,0,0,0,0}。
从图3结果看出,由于方位失准角与两个水平失准角之间的误差有所差异,所以导致收敛速度要慢,
精对准下姿态角误差的仿真结果如图4所示。
由图4可知,运用该方法进行初始对准,对准精度比较高,对准结束后,3个姿态角分别为59.995 6°,80.017 8°和69.884 4°,提高了对准精度。
4 结 语

图3 平台失准角误差曲线图 图4 精对准下姿态角误差
捷联惯导系统的初始对准是以系统误差模型为基础,利用解析方法快速粗略地估算出初始姿态矩阵,再将卡尔曼滤波运用到精对准中,对系统误差进行分析,并将系统失准角从干扰误差中估算出来,有效解决了对准时间和精度之间的矛盾。从实验仿真可以看出,运用本文所设计的方法,大大减少了对准时间,对准精度也得到了明显的提高。
[1] 丁继成,李冠男,班镜超.基于双轴位置转台的捷联惯导系统级标定技术[J].舰船科学技术,2015,37(4):76-78.
[2] 马龙华,王凯利.动基座条件下捷联惯导系统初始粗对准新方法[J].弹箭与制导学报,2013,33(3):1-4.
[3] 高贤志,王丹.单轴旋转式惯导系统误差抑制机理分析[J].舰船科学技术,2012,34(8):67-72.
[4] 高延滨,管练武,王庭军.单轴旋转式光纤捷联惯导系统定位精度分析[J].仪器仪表学报,2014,35(4):794-800.
[5] 贾继超,秦永,张波,等.系统随机噪声对捷联惯导初始对准影响分析[J].传感技术学报,2013,26(12):1715-1718.
[6] 徐梓峰,卢艳娥,庞春雷.基于GPS的捷联惯导系统误差校正研究[J].计算机测量与控制,2013,21(9):2518-2521.
[7] 周聪,肖建,王嵩.多采样率卡尔曼滤波器在汽车状态估计中的应用[J].西南交通大学学报,2012,47(5):849-854,894.
[8] 李鹏辉,刘小雄,徐恒,等.基于无迹卡尔曼滤波的迎角/侧滑角估计方法[J].测控技术,2014,33(3):140-143.
[9] 丁继成,陈帅.捷联惯导系统方位失准角对准技术研究[J].计算机仿真,2013,30(1):132-136.
[10] 敖志刚,唐长春,付成群,等.多传感器自适应容积卡尔曼滤波融合算法[J].计算机应用研究,2014,31(5):1312-1315,1331.
[11] 冯杨,徐庆九.激光陀螺捷联惯导系统的误差参数标定方法[J].测控技术,2013,32(4):126-130.
[12] 严恭敏,张强,何昆鹏,等.捷联惯导系统中加速度计的时延补偿研究[J].宇航学报,2013,34(12):1578-1583.
[13] 郜福全,陈丽容,丁传红,等.UD分解自适应滤波在SINS初始对准中的应用[J].计算机工程与设计,2014,35(1):158-162.
High Precision Initial Alignment Method of Stationary Base in Strap-down Inertial Navigation System
WANG Xuerui, ZHOU Yan
(Henan Institute of Engineering, Zhengzhou 451191, China)
In order to deal with low accuracy of the stationary base in the strap-down inertial navigation system initial alignment, the author proposed a method of using accelerometers and gyroscopesthe to measure the Earth′s gravity vector and angular velocity vector, and using the analytical method to estimate directly the initial posture matrix which meets the requirements for use. Then, the error is analyzed by Kalman filter model and a state equation and a measurement equation are established to estimate the system misalignment angle from interference error, that provides the accurate initial conditions for the navigation calculation. The simulation results show that the introduction of the Kalman filter into the high-precision initial alignment of stationary base in the strap-down inertial navigation system improves the alignment accuracy and convergence rate significantly.
SINS; stationary base; initial alignment; Kalman filter; precision alignment
2016-09-22
王雪瑞(1977-),女,河南登封人,硕士,副教授,主要从事计算机应用与嵌入式技术方面的研究.
10.3969/i.issn.1674-5403.2017.01.019
TP273.4
A
1674-5403(2017)01-0070-05

